弹载雷达导引头测高回波模型仿真研究
2018-11-21何华锋戴嘉琪
何华锋, 戴嘉琪, 贺 友
(火箭军工程大学,西安 710025)
0 引言
雷达测高技术最初在20世纪60年代被应用于全球海洋观测[1],主要测定海平面高度和研究大洋环流。近年来,随着技术的不断融合以及武器装备的快速发展,雷达测高技术不仅仅应用于卫星高度计和机载雷达高度计,而且被逐步应用于导弹等新型武器装备。文献[2]针对导弹景象匹配定位中高度通道数据不可观的问题提出了高度辅助的INS/SAR组合导航算法;文献[3]提出一种基于雷达导引头测高数据与惯导数据融合的导弹战斗部爆高控制方法。
目前国外多种型号的导弹武器均采用雷达景象匹配的末制导方式,由弹载雷达高度计测得的高度值来确定导弹的空间高度,结合景象匹配提供的导弹平面二维坐标,来进行弹-目位置定位,完成对惯导数据的修正。因此,雷达测高精度对于导弹末制导实现精确打击至关重要。目前弹载雷达高度计的试验鉴定以挂飞试验为主,但是其试验周期长、消耗资源多,所以将仿真与试验相结合的鉴定方法是目前的趋势。文献[4]提出了弹头自旋模式下的脉冲多普勒地面回波的建模与仿真方法;文献[5]将目标信号、杂波和噪声3种回波信号叠加,提出了一种快速模拟仿真雷达回波的方法。
然而在实战条件下,雷达测高面临着复杂的外部环境。对于战术地地导弹,其打击目标多为丘陵山地,所以地形起伏是雷达导引头测高面临的最主要因素。但目前针对地形起伏、外部电磁干扰等环境条件的雷达导引头测高回波仿真研究还比较少,特别是对于导弹再入段的测高回波仿真。
针对以上情况,本文建立复杂地形条件下的单脉冲线性调频雷达在导弹再入段的测高回波模型,对其进行仿真并通过BROWN提出的回波抽象模型[6]来进行验证。
1 回波模型
弹载雷达导引头测高原理与传统雷达高度计测高原理相同,都是利用回波延迟来计算高度,通过高度跟踪算法完成测高。为了仿真出弹载雷达导引头的测高过程,必须首先从其点目标回波模型入手。
1.1 点目标回波模型
如图1所示,不考虑天线误指向角,以导引头测高天线波束垂直照射的天底点O为原点,建立平面直角坐标系。导弹弹道始终处于射面y-z内,其飞行再入段弹下点轨迹为L,v为t时刻弹下点所对应的切向速度,测高天线在点P(xp,yp,h)处向波束照射范围内的点A(xa,ya,za)发射单脉冲线性调频信号,斜距为R,两点连线与切向速度v的夹角为θ。

图1 雷达导引头测高观测模型Fig.1 Altimetry observation model of radar seeker
设发射信号的时宽为T,信号载频为f0,带宽为B,调频斜率为K=B/T。实际上测高天线以重复周期T0发射脉冲信号,为仿真简便,本模型只考虑单脉冲周期内的回波信号;同时,由于弹载雷达高度计一般在2~10 km高度内进行测高,高度较低,回波延迟很短,因此不考虑在回波延迟内的导弹运动距离。所以发射的线性调频信号(LFM)可表示为
s(t)=φ(t)ej 2π f0t
(1)
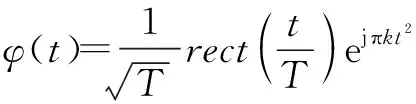
(2)
由于此刻导弹正处于末制导再入段,即高速运动阶段,需要考虑与目标点径向速度产生的多普勒频移fD,即
fD(θ)=2vcosθ·f0/c
(3)
式中:c为光速;θ为径向速度与切向速度的夹角。对于天线波束照射区域内一点A的回波信号可以表示为
(4)
式中:M为点目标回波增益;td为双程延迟。
(5)
td=2R/c
(6)
式中:λ为雷达波长,目前弹载雷达高度计大多工作于Ku或C波段,以Ku波段雷达频率15 GHz为例,其波长约为2 cm;G为天线增益,其值与雷达高度表本身以及偏离天线中心轴的角度有关;γ为复散射系数,与σ(雷达截面积)不同的是,γ既包含幅度信息,也包含相位信息,即
(7)
需要注意的是,由于地形起伏,A点的高程不一定为0,所以A点并不一定处于x-y平面,则目标点与弹下点的距离为
(8)
综合式(1)~式(8),点目标的回波信号为
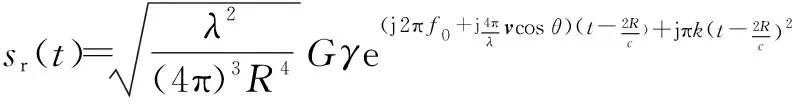
(9)
1.2 脉冲压缩
为提高雷达导引头测高的距离向分辨率,需要对接收到的回波信号进行脉冲压缩处理。常用的脉冲压缩技术[7]有全去斜和匹配滤波技术。本文采用匹配滤波技术对回波信号进行脉冲压缩。
由线性调频信号的复包络φ(t)可知,其模糊函数为
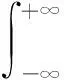
(10)
由式(10)很明显可以看出,其模糊函数经过转换可以表示为回波信号经匹配滤波后的输出。又因为
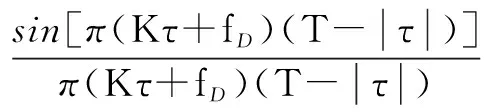
(11)
所以可得到经过脉冲压缩后的回波信号为
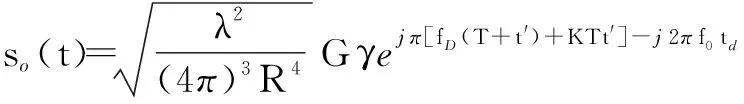
(12)
式中,t′=t-td。
至此,已得到经过脉压处理的点目标回波信号模型。
2 地面模型
在得到回波信号模型后,就需要建立地面模型,包括目标地形的分割、地面后向散射系数的计算以及相关矢量与夹角的计算。
2.1 地面散射模型
在上一节建立点目标回波模型时提到了雷达截面积σ,对于单位散射体就需要考虑单位雷达截面积,即后向散射系数为
σ0=σ/S
(13)
式中,S为天线波束所照射的大地面积。
雷达截面积是描述散射体散射特性的物理量,其与信号入射角、地形地貌均有紧密联系。
为便于仿真,本文做以下两点假设:1) 被照射的大地表面可以看作是所有散射体的集合,并且各个散射体相互独立;2) 大地表面的覆盖植被与地形种类均相同,仅考虑入射角对后向散射系数的影响。
文献[8]介绍了WANNER推导的描述大地平均后向散射系数的公式
(14)
式中:α为与散射体有关的参数;σh表示地面起伏的方差,但由于此方程过于复杂,本文采用近似方程
σ0(β)=n/4·cosnβ
(15)
为便于仿真,取n=4,此时
σ0(β)=cos4β
>。
(16)
图2显示了当n=4时,后向散射系数与入射角之间的关系。

图2 后向散射系数曲线Fig.2 Curve of backscatter coefficient
2.2 目标地形的建立与分割
弹载雷达是利用天线波束范围内的大地回波功率进行测高计算的,所以可以将总的回波功率看成是地面网格各点回波功率的叠加。
从某丘陵地带的实际地面高程中抽取300 m×300 m的点集矩阵,由于分辨率并不能满足仿真要求,为提高仿真精度,采用基于Delaunay三角剖分原理[9]的逐点插入Lawson算法[10]将地形分为若干个三角散射网格。如图3所示,与正方形网格划分法相比,Delaunay三角形具有空圆特性,即任意4点不共圆,各散点组成的三角形外接圆内不会包含第4个点。

图3 Delaunay三角剖分Fig.3 Delaunay triangulation
上文提到弹载雷达高度计一般工作在2~10 km高度内,以工作在2 km高度、天线波束宽度为10°为例,其波束照射面积约为200 m×200 m。根据上述原理与算法,本文仿真时截取如图4所示的经过Delaunay三角剖分的200 m×200 m数字地形图,地形服从高斯分布,其高度散布均方根值为σs=1.097 5 m。

图4 仿真用数字地形Fig.4 Digital elevation terrain
2.3 散射单元模型

(17)
地形坡度为
(18)
则散射单元面积为
S=S0/cosα
>。
(19)
综合式(13)、式(16)、式(17)、式(18)和式(19)可以求得该散射单元的雷达截面积σ。
图5 散射单元模型Fig.5 Scattering cell model
3 回波功率
在实际情况中,地面总回波是所有地面散射点回波的矢量叠加。但是在仿真中,网格的精度无法算得每个回波的相位,为了能够反映出具有统计意义的回波起伏变化,仿真中每个时刻的回波功率是相应时刻所对应的等距离散射点回波功率的标量叠加。则t时刻接收到的回波功率信号为
(20)
式中,i为t时刻等距离散射点的个数。
4 回波仿真
以图3所示数字地形为目标地面仿真模型,利用三角剖分算法分割为1682个Delaunay三角网格,每个网格在x-y平面内的投影面积约为S0=22 m2,测高天线高度h=2 km,导弹再入段速度v=600 m/s,发射的线性调频信号时宽T=10 μs,信号载频f0=300 MHz,带宽B=60 MHz,回波信号采样频率为300 MHz,仿真的单脉冲回波信号功率如图6所示。
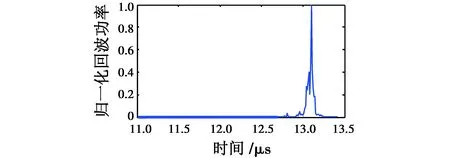
图6 仿真结果Fig.6 Simulation result
从图6中可以较为清楚地看出回波起伏的细节,以发射脉冲信号的时间为零点,接收机从12.6 μs开始接收到回波信号,在13.1 μs达到回波功率峰值。
5 模型验证
对于本文提出的测高模型,采用回波的通用模型进行验证。BROWN在1977年提出了粗糙表面平均脉冲响应模型[6],其表面的回波功率可以表示为
PR(τ)=q(τ)·PFS(τ)·sr(τ)
(21)
式中:q(τ)为地面高度概率密度函数;PFS(τ)为平坦地面的平均冲激响应函数;sr(τ)为雷达的冲击响应。更具体地,对于使用脉冲压缩技术的典型窄脉冲雷达,还可以进一步简化为
(22)
式中
(23)
σP=0.425T
(24)
(25)
式中:η为脉冲压缩系数;PT为发射功率峰值;σP为点目标的3 dB时间宽度;γ为高斯天线参数;ξ为天线误指向角,由于本文不考虑误指向角,所以在仿真时取极小值;I0( · )为第一类Bessel函数;erf( · )为误差函数。
需要注意的是,使用此通用模型来仿真需要满足以下5个条件:1) 散射表面可以被看作是一系列随机的独立散射单元;2) 在波束照射范围内的地表的高程数据在回波时间内固定不变;3) 整个散射过程是一个没有极化效应的标量过程,并且与频率无关;4) 整个散射过程只与入射角和后向散射系数有关;5) 雷达与任一散射单元的径向速率引起的多普勒频移远远小于发射脉冲的频率。很明显,本文是满足上述5个条件的。
图7显示仿真所得的回波功率曲线和基于粗糙表面平均脉冲响应的Brown回波模型曲线。与仿真所得曲线相比,Brown回波曲线更加平滑,在13.06 μs达到峰值,更清晰地显示出其上升沿和下降沿的变化情况,但对于回波的起伏情况反映较差。总体来说,两者曲线的符合度较高,基本确定本文模型的适用性与合理性。
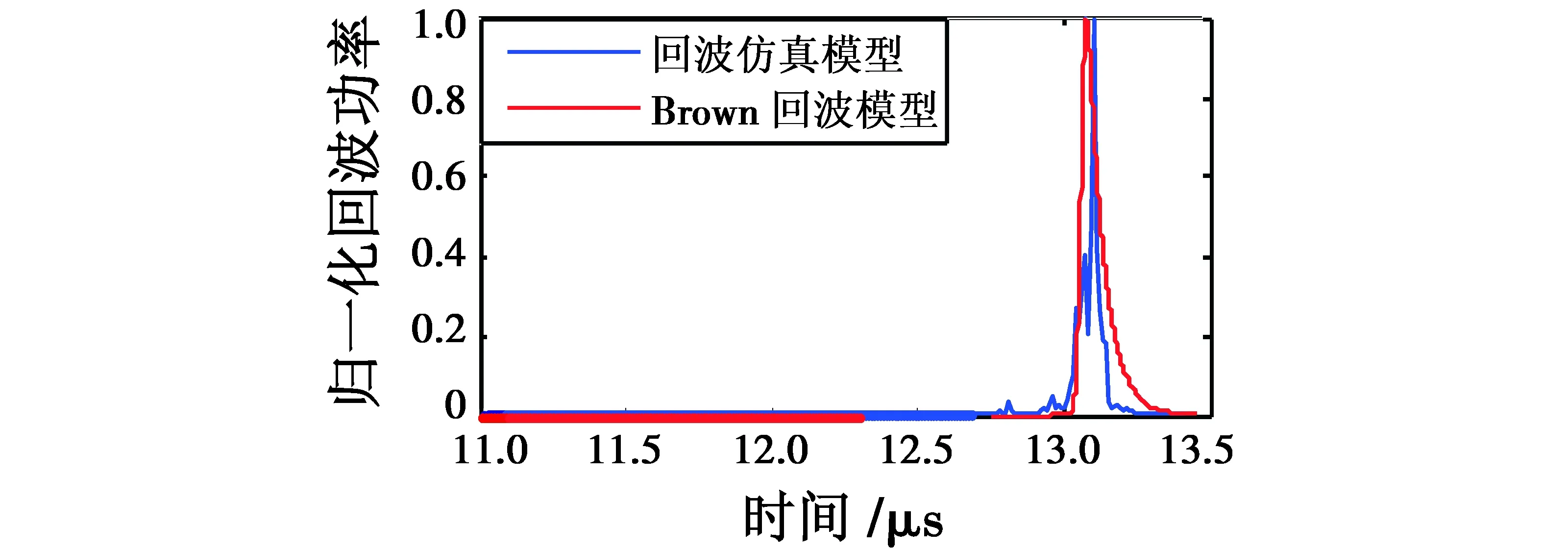
图7 两种模型的回波功率比较Fig.7 Comparison of two kinds of echo models
6 结束语
本文对目前雷达测高试验鉴定中存在的不足进行了分析,针对复杂地形建立了导弹在末制导再入段高速飞行时的点目标回波模型。在保证仿真精度的前提下,基于真实地形,采用三角剖分的Lawson算法将数字高程地形划分为若干个三角网格进行仿真;为说明模型适用性,采用抽象回波模型进行比较验证,最终证实了此模型的正确性与合理性,为下一步基于复杂地形与外部干扰条件下的雷达测高试验鉴定仿真工作奠定了良好的基础。
