基于Dubins路径的A*算法的多无人机路径规划

宋雪倩， 胡士强

(上海交通大学，上海 200240)

0 引言

无人机(Unmanned Aerial Vehicle,UAV)已经被广泛运用于民用和军用领域。为了达到真正的“无人”和“智能”，在环境已知并给定起始位置和航向角之后，无人机应能够自主规划一条满足任务需求的避障路径，通常要求这条路径最短；而当空中有两架无人机在同一高度执行任务时，必须考虑防撞，同时还要满足飞行性能约束。对于固定翼无人机，它们不能像旋翼机一样悬停，必须保持最小速度，且转弯受到最小转弯半径的限制。

A*算法[1]是路径规划中最著名的离散搜索算法之一。通常先将二维平面进行栅格化，再使用A*算法或改进A*算法进行最短路径搜索[2-3]。这在规划时没有考虑飞行器的始末航向要求，得到的路径不能满足飞行性能约束且会对一些不必要节点进行搜索。文献[4-5]都使用了A*算法进行移动机器人的路径规划，都是在规划完成之后，对路径进行光滑处理，其中涉及较大计算量且无法保证光滑之后的路径依旧安全；文献[6]考虑了飞行性能限制，利用可视图法与 Dijkstra算法，但仍需要较长计算时间；而Dubins路径[7]是给定始末方向以及在转弯半径有约束的情况下、两点之间的最短曲线，被广泛用于自主机器人的路径规划当中[8-10]。本文提出的基于Dubins路径的A*算法的路径规划方法，考虑了固定翼无人机的最小转弯半径，利用Dubins路径进行可飞路径建模，以Dubins曲线与障碍圆切入点，即无人机的位姿为节点，边搜索下一步的有效节点，边利用A*算法进行寻优，由于剔除了不必要节点，提升了搜索效率。在两架固定翼无人机处于同一高度飞行的情况下，利用两机之间脱靶距离大小判断冲突，结合向量共享法(Vector Sharing Resolution)[11]，在线调整航向并进行路径重规划，可以得到两者的安全航迹。

1 Dubins路径

1.1 Dubins路径

Dubins路径定义为：在最大曲率限制下，平面内两个有方向的点间的最短可行路径是CLC路径或CCC路径，或是其子集，其中，C表示圆弧段，L表示与C相切的直线段[9]。这里只考虑CLC型路径，如图1所示。

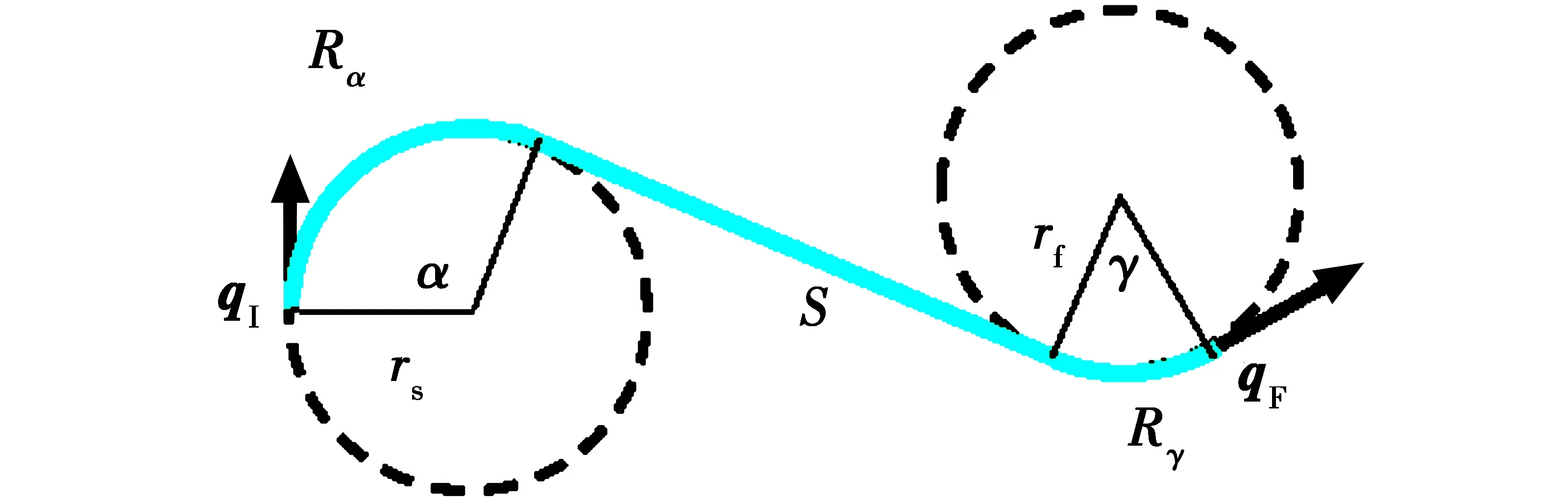
图1 一种CLC型Dubins路径Fig.1 Dubins path of the CLC type

1.2 CLC型Dubins路径存在的充分条件

如果两个位姿分别对应的两个Dubins圆之间存在内外切线，即

|rs+rf|>|c|

(1)

则CLC型Dubins路径一定存在。式中:rs为起始圆弧半径;rf为终止圆弧半径。当满足这个条件时，则称两个位姿之间在给定起始和终止圆弧半径情况下，最短CLC型Dubins路径为Dubins路径。

1.3 Dubins路径的长度

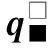
L(qIqF)=Rα+S+Rγ

>。

(2)

1.4 基于Dubins路径的避障

当路径不安全时，无人机有2种避障方法：顺时针(CW)绕过障碍圆(如图2绿线所示)或逆时针(CCW)绕过障碍圆(如图2蓝线所示)。

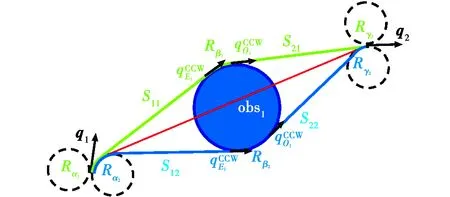
图2 基于Dubins路径的两种避障方法Fig.2 Two possible Dubins paths to avoid an obstacle

2 基于Dubins路径的A*算法的路径规划

具体规划流程如图3所示。

图3 基于Dubins路径的A*算法的路径规划流程图Fig.3 The flow chart of planning a path by Dubins-path based A* algorithm

假设环境已知，所有障碍物分散且可以用圆来建模。当所有障碍圆之间均满足CLC型Dubins路径存在的充分条件情况下，即可用本文方法进行路径规划。路径规划中加入了A*算法的启发式特点。

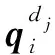
(3)

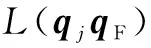
3 多无人机防撞方法

假设两架固定翼无人机在同一高度飞行，且实时位姿、速度等状态都相互可知。首先可对两者分别用基于Dubins的A*算法进行路径规划，在按照此路径飞行过程中进行相撞判断并采取改变航向角的措施从而防止相撞，确认不会相撞之后，再利用第2章所述算法分别对两者进行航迹重规划。

3.1 相撞检测

最接近时间为

(4)

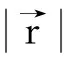
如图4可得，两架无人机之间脱靶距离为

(5)

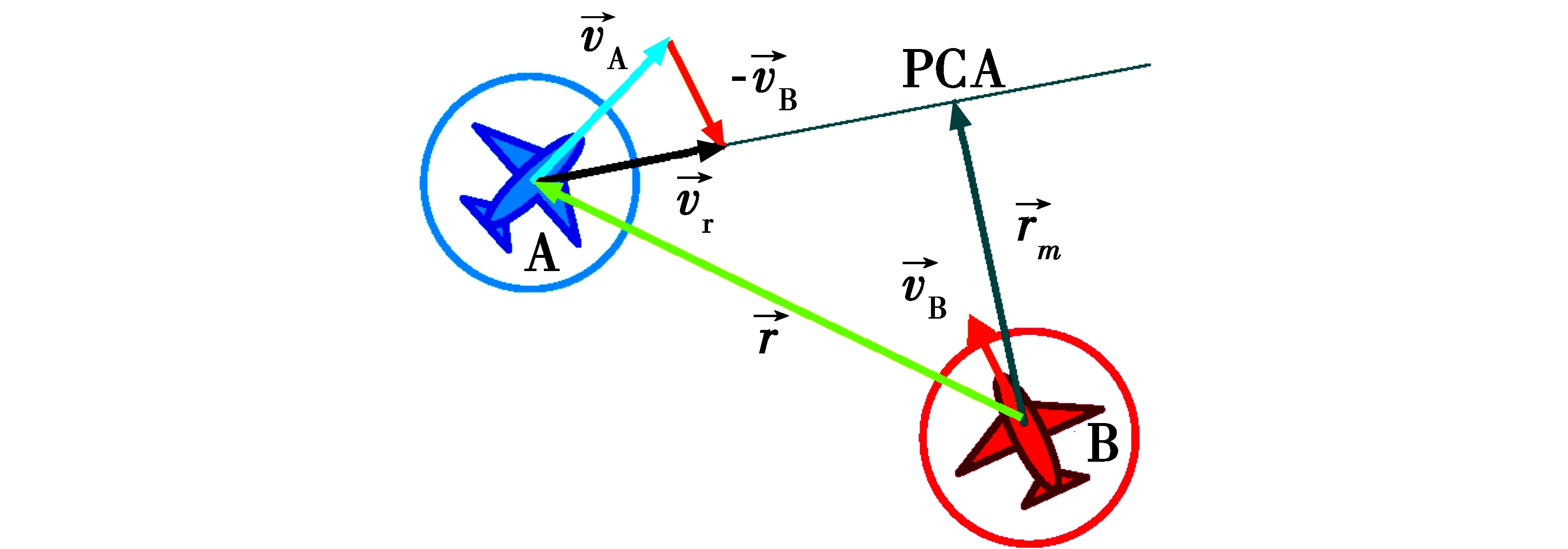
图4 两架无人机的相对运动状态Fig.4 The relative motion between 2 UAVs

3.2 防撞措施

(6)

对无人机A有

(7)

对无人机B有

(8)

设无人机将以最小转弯半径进行速度方向改变，为了保证两架无人机在改变方向时不发生碰撞，在速度改变时，要满足

(9)

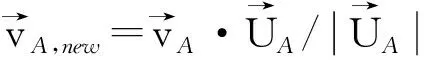
图5 向量共享法防撞方法Fig.5 Collision avoidance by Vector Sharing Resolution

4 仿真验证

4.1 单无人机避障路径规划

区域中共有4个障碍物O1～O4，其位置和半径分别表示为：Oobs1=(25>10>3),Oobs2=(25 23 4),Oobs3=(39>31>0.8),Oobs4=(41>40>3)。A的起始位姿qA,s=(20 m>0 m>60°)，目标位姿qA, f=(45 m>0 m>60°)。

图6中红线为所得路径，由4段Dubins路径组成，长度为67.9 m，且路径光滑。在相同条件下，将地图进行离散，如图7所示，蓝线为通过A*算法规划所得结果，路径长度为71.1 m，其长度大于图6中结果，且路径不够光滑，不能直接投入实际应用。

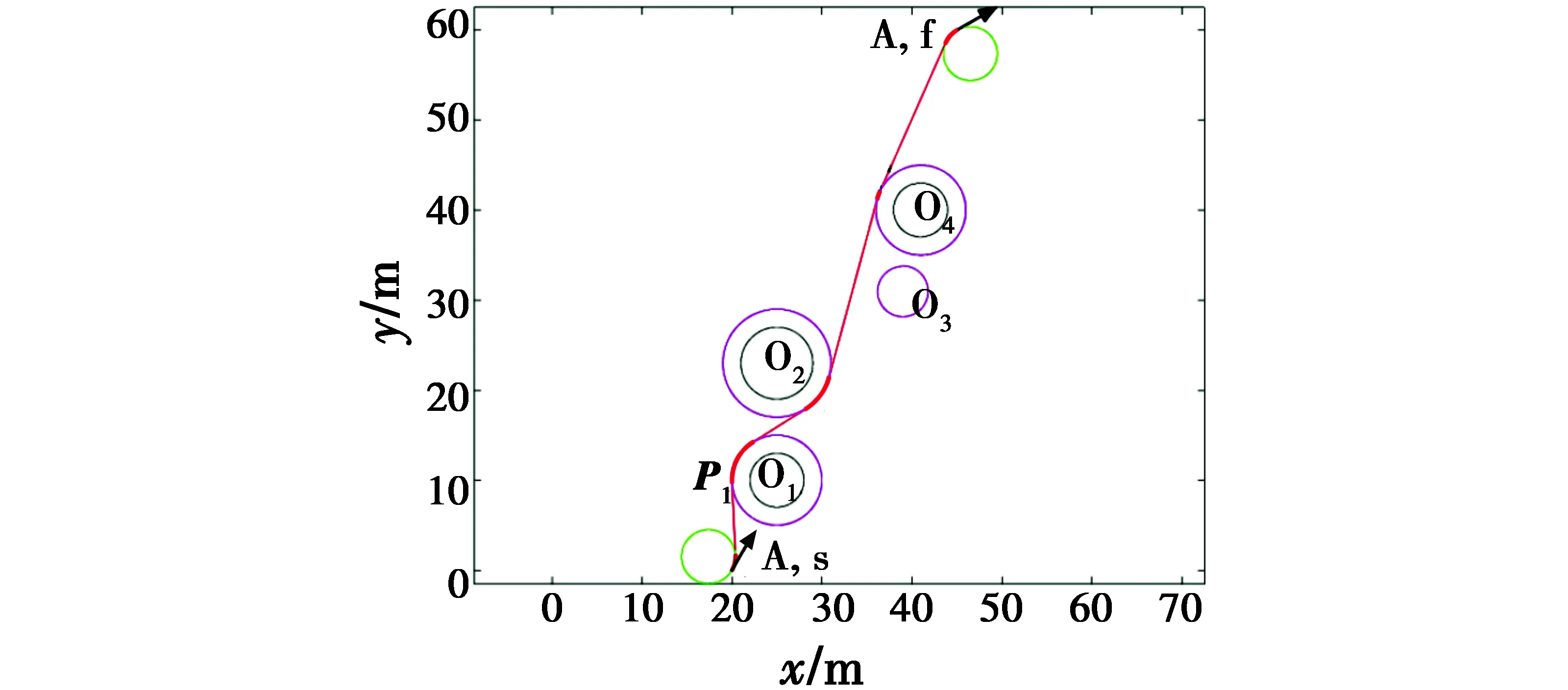
图6 基于Dubins的A* 算法的路径规划仿真结果Fig.6 The path planning simulation result for single UAV by Dubins-path based A* algorithm

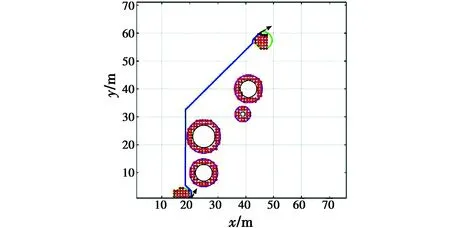
图7 基于网格地图的A*算法路径规划Fig.7 Path planning by A* algorithm applied on a grid map

4.2 双无人机避障防撞路径规划

区域中共有4个障碍物O1～O4，其位置和半径分别表示为：Oobs1=(35>23>4.2),Oobs2=(35>10>3),Oobs3=(49>31>0.8),Oobs4=(35>45>3.2)。A的起始位姿qA,s=(30 m>0 m>60°)，目标位姿qA,f=(55 m>60 m>60°);B的起始位姿qB,s=(0 m>0 m>30°) ,目标位姿qB, f=(80 m>65 m>30°)，状态采样频率为20 Hz。

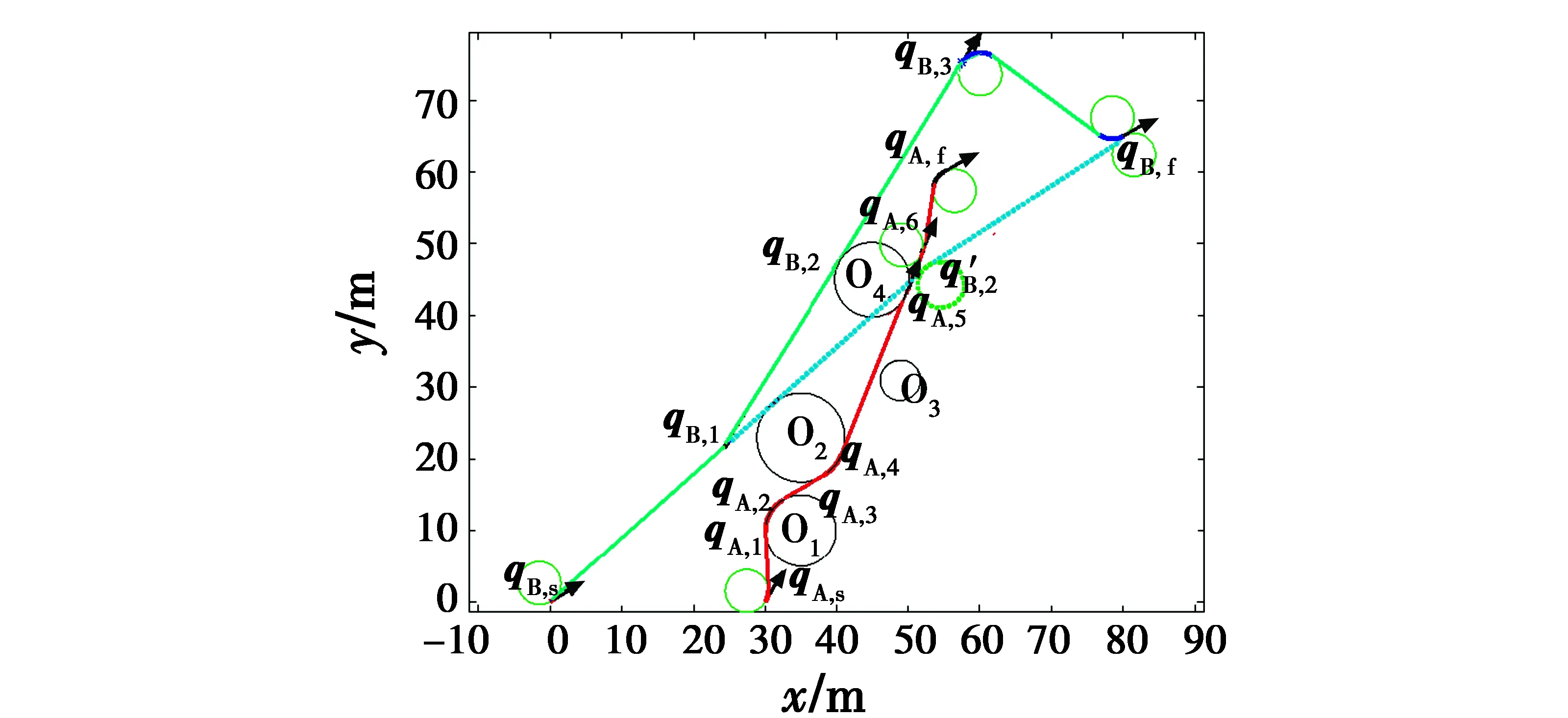
图8 基于Dubins的A* 算法的双无人机路径规划仿真结果Fig.8 The simulation result of path planning for2 UAVs by Dubins-path based A* algorithm

图9为两架无人机之间距离的示意图。其中，绿线为两者最小安全距离,蓝线为两者按照各自所规划的路径飞行时的距离。如果按照原始路径飞行，在5.5 s左右，两者会碰撞。而如果采取了防撞规避，则两者会在2.85 s采取规避措施，改变速度。两架无人机之间最小距离为13.15 m，不会发生相撞。

图9 两架无人机之间距离Fig.9 The distance between 2 UAVs

5 结束语

本文提出了一种基于Dubins路径的A*算法的多无人机航迹规划方法。利用Dubins路径、环境中的有效节点，再利用A*启发式算法的思想进行路点确定，有效提高了航迹规划的效率，且考虑了固定翼无人机的飞行性能限制以及保证得到的路径光滑；在两架无人机同一高度飞行的情况下，结合向量共享方法，解得防撞避障所需偏航角度，调整航线，确保没有相撞危险后，再进行重规划。仿真表明，此方法所得路径优于传统A*算法，且在双无人机同一高度飞行时可以得到安全可飞行路径。

本文的多无人机情况，仅考虑了两架无人机的情况以及航迹安全和避障等基本问题，在下一步研究中将研究如何优化每条无人机航迹,并且考虑如何拓展至更多无人机执行复杂任务的情况。