基于Back-Stepping鲁棒自适应动态面的近空间飞行器控制

徐文萤, 江 驹， 甄子洋, 李 欣

(1.南京航空航天大学自动化学院,南京 210016； 2.空间物理重点实验室，北京 100076)

0 引言

近空间可变翼飞行器又称高超声速可变翼飞行器，是指在近空间区域内飞行且飞行器机翼外形结构可变化的飞行器。由于其在军事装备、科学探索和未来航天运输领域均具有重要的潜在应用价值，对于可变翼飞行器的研究得到了国内外众多学者和研究机构的重视。高超声速飞行器采用翼身融合构型，具有激烈快时变、强耦合、严重非线性、不确定性等动态特性,给飞行器的控制带来了困难[1-4]。同时，由于飞行环境复杂，近空间可变翼飞行器还受到自身气动参数不确定和外界环境干扰的影响。因此，近空间可变翼高超声速飞行器在飞行控制系统设计、鲁棒性研究方面都面临着重大考验[5-8]。

由于高超声速飞行器具有高度非线性特性，采用传统的小扰动线性化方法难以进行设计。在高超飞行器模型建立方面，文献[9]对近空间飞行器的气动力特性和气动弹性等进行了详细的剖析，为后续的飞行器模型建立奠定了理论基础;文献[10]在飞行器结构和空气动力学基础上展开分析，建立了吸气式高超声速飞行器的模型，为下一步的控制器设计提供了可用的数学模型;文献[11]实现了高超声速飞行器动态逆方法的高度控制，但是该方法不具备对参数和模型变化的鲁棒性;文献[12]将动态逆和反步法相结合设计飞行控制系统，解除强耦合，保证全局稳定性;文献[13]利用高超声速飞行器动态逆模型设计鲁棒滑模控制方法，但是该方法容易在滑模面产生抖振;文献[14-16]根据严反馈形式，设计Back-Stepping;文献[17-18]引入了动态面控制，解决了因为多重递推产生的“微分膨胀问题”。

本文首先通过对可变翼高超声速飞行器在巡航段的气动参数插值拟合，对实际飞行环境建立严反馈纵向模型；然后针对Back-Stepping控制方法鲁棒性不够等问题，提出一种基于Back-Stepping的鲁棒自适应动态面控制策略，采用神经网络RBF方法逼近模型中的未知函数部分，通过对不同中心点取值，并且对宽度和权重进行调节，实现在线实时更新参数，使得系统具有更强的自适应能力,并结合动态面控制方法，克服了传统递推设计时的控制器微分项数的膨胀问题。该策略为高超声速飞行器纵向模型设计跟踪控制器，以求保证系统的半全局稳定有界并抑制外界不确定因素的扰动，具有较强的鲁棒性，从而确保高超声速飞行器安全飞行，最后进行数值仿真验证。

1 近空间可变翼飞行器纵向建模

1.1 非线性数学模型

如图1所示，本文研究的近空间可变翼飞行器采用翼身融合布局，机体外形轮廓呈三角形，大后掠机翼，机翼后缘布置升降舵，机翼两侧存在可形变的翼面，采用对主翼两侧的小翼进行伸缩控制的方式，提高飞行器升力、提升飞行效率、减少能耗等。

该飞行器在高超声速巡航飞行条件下的纵向运动模型描述为[19-20]

(1)

气动力和力矩分别表示为

(2)

式中:V为飞行速度;h为飞行高度;γ为航迹角;m为飞行器质量;α为迎角;q为俯仰角速率;L为升力;D为阻力;T为发动机推力;s为飞行器固有参数面积;r为地球半径;μ为地球引力参数;Myy为俯仰力矩;Iyy为转动惯量。

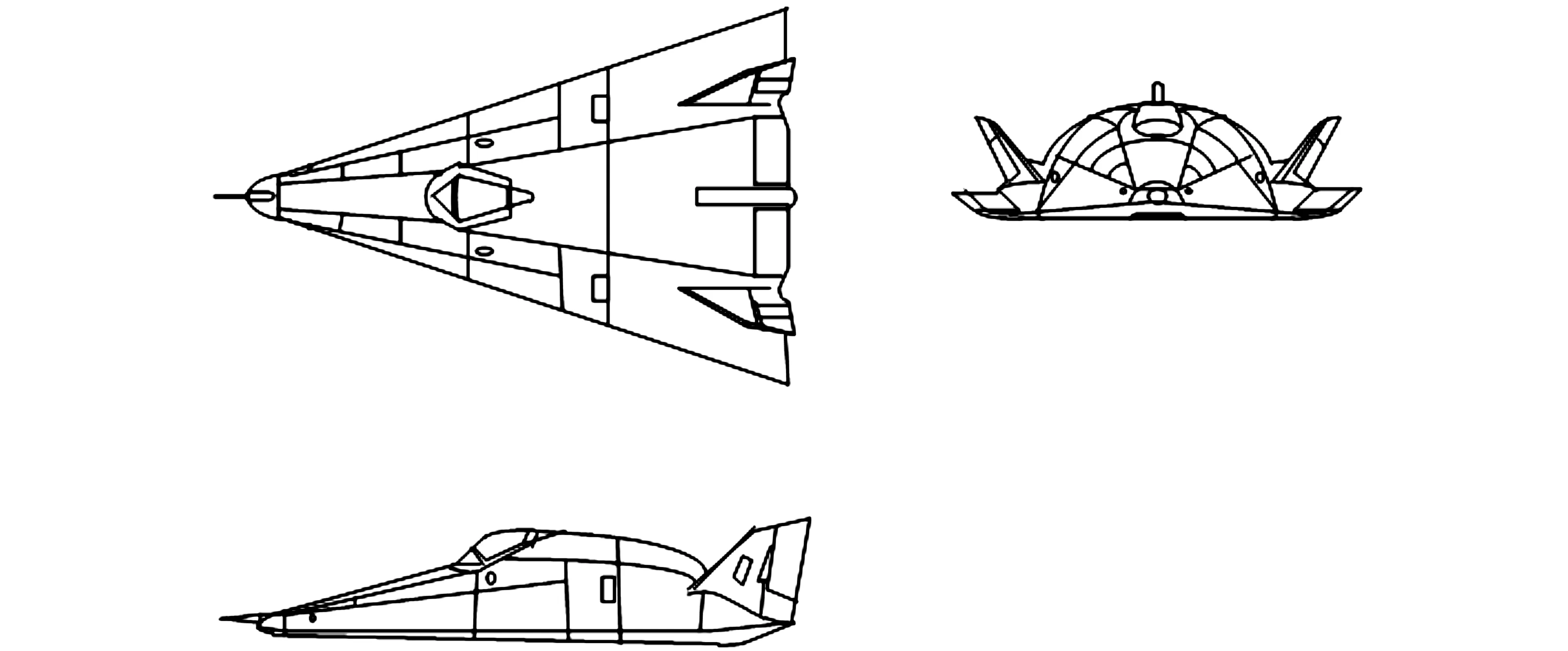
图1 近空间可变翼飞行器视图Fig.1 View of near space variable-wing aircraft

可变翼飞行器为模型带来的影响主要体现在气动参数的变化上。根据近空间可变翼飞行器在巡航段飞行气动特性的经验公式可以得到气动数据随着迎角、马赫数变化的函数关系，对已知的小翼伸出和小翼收回的部分气动参数C1,C2和C4插值拟合得到巡航段下飞行器的气动参数，最终建立准确的近空间可变翼飞行器纵向巡航段模型。在可变翼飞行器起飞爬升段为了增大升力，使用小翼伸出方式增大升阻比。在可变翼飞行器巡航段为了减小阻力，使用小翼收回方式，减小阻力气动导数，减少耗能。图2和图3给出了升力系数C1和阻力系数C2与马赫数Ma和迎角α的关系。

发动机推力算式为

T=0.5ρV2sC3

(3)

式中,C3为推力系数， 且

(4)

发动机动态方程采用二阶系统模型为

(5)

该模型的控制输入为发动机节流阀调定值βc和升降舵偏转δe。

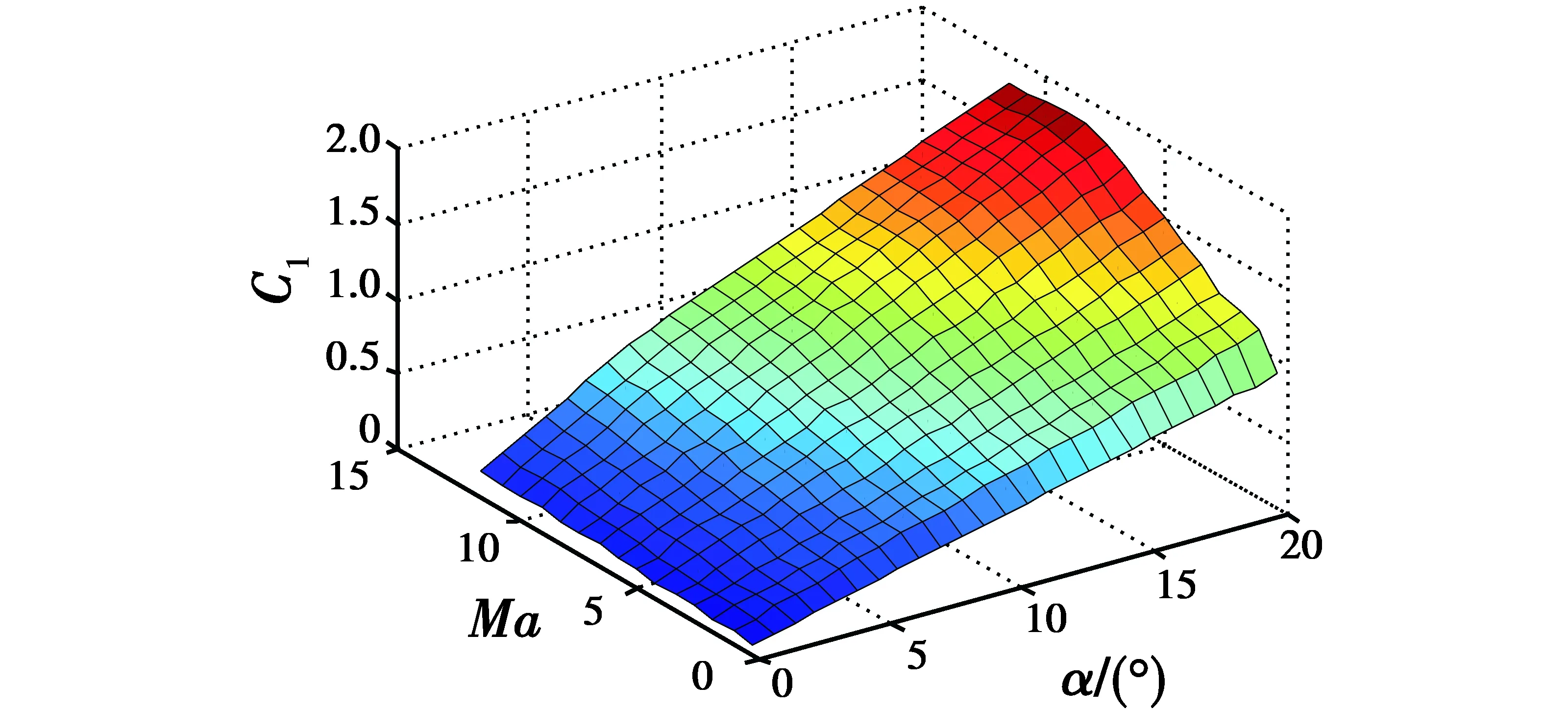
图2 升力系数Fig.2 Lift coefficient

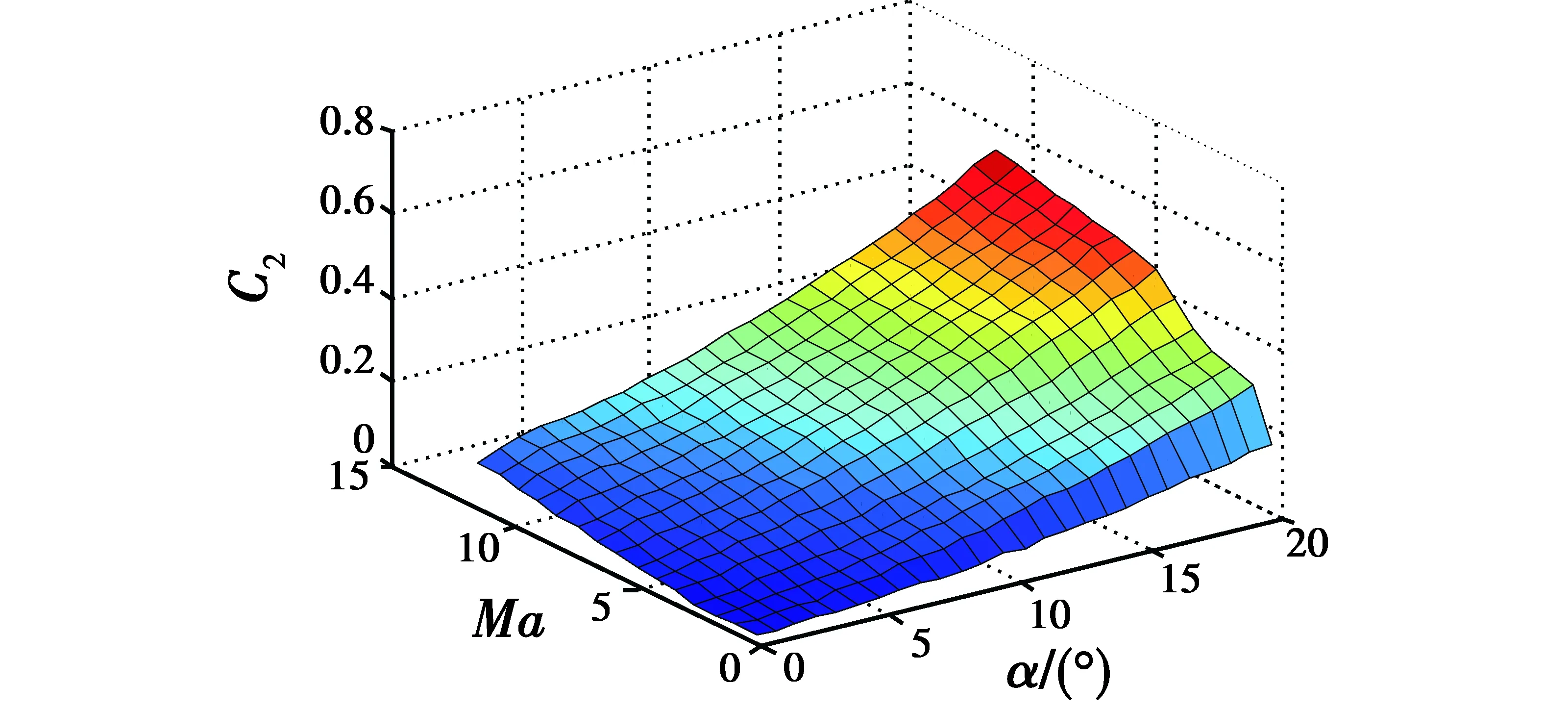
图3 阻力系数Fig.3 Resistance coefficient

1.2 超声速严反馈形式

由式(1)可以看出，高度的变化主要与升降舵舵偏角δe相关联，而速度的变化主要与油门控制量β相关联，因此可以将高度控制器与速度控制器分开设计。为了得到严反馈形式下的高超声速飞行器数学模型，可做如下几个假设。

假设1高超声速飞行器在巡航段的飞行速度变化较慢，且变化范围较小。

假设2式(1)中的推力项Tsinα远远小于升力项L，可近似认为Tsinα≈0。

假设3航迹角很小且满足sinγ=γ。

定义x1=γ,x2=θ,x3=q,其中θ=α+γ,μ=δe，代入式(1)可以得到严反馈形式，即

(6)

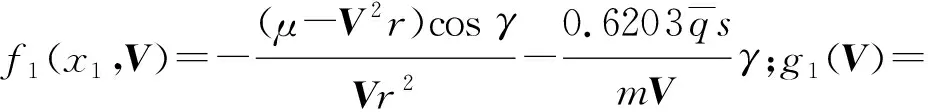
2 基于Back-Stepping的鲁棒自适应动态面控制器设计

基本的Back-Stepping控制方法是引入一系列虚拟控制量，通过多步的递归计算求得系统的控制信号，同时,基于Lyapunov稳定性理论设计的控制器能够保证闭环系统所有信号有界。

基于Back-Stepping的鲁棒自适应动态面控制器结构如图4所示。

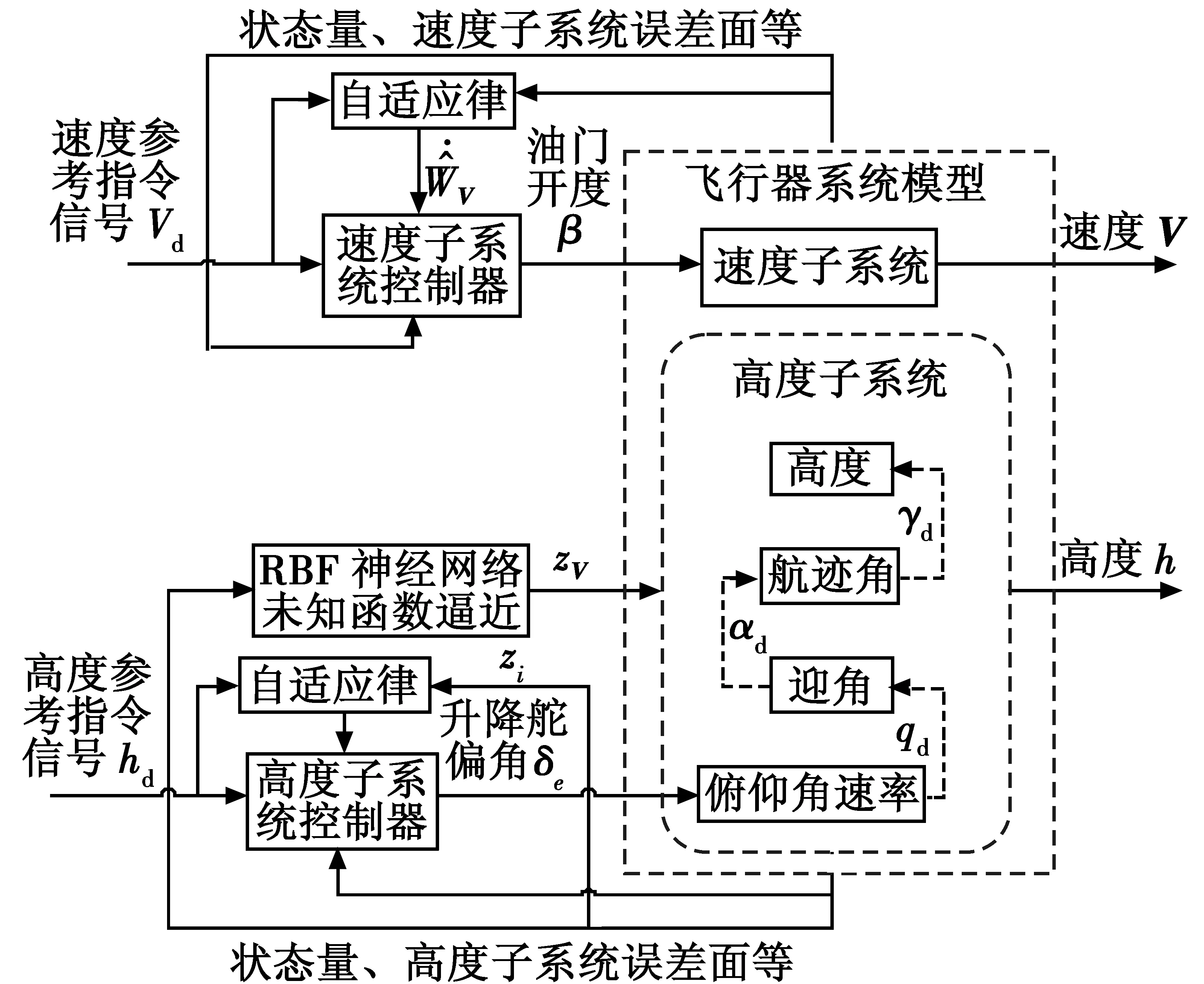
图4 高超声速飞行器Back-Stepping鲁棒自适应动态面控制器结构图Fig.4 Back-Stepping robust adaptive dynamic surface controller of hypersonic vehicle

2.1 高度控制器设计

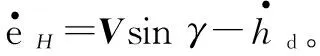
(7)

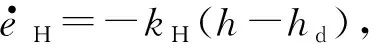
假设近空间可变翼飞行器在巡航段飞行状态下，飞行器固有参数飞机表面积s、质量m、翼弦长c、俯仰力矩惯性积Iyy、升力系数C1、阻力系数C2，俯仰力矩系数C4等都存在一定的摄动。由小翼伸缩变化、飞行测量误差、环境影响等引起的参数不确定性部分等用一个附加变化Δ来表示，即

(8)

根据上面的严反馈形式，受扰动近空间可变翼飞行器纵向动力学模型可以改写为

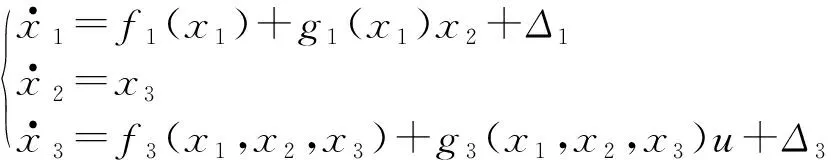
(9)

式中,Δ表示由上述飞行器固有参数、气动参数摄动和外界环境干扰等构成的不确定影响。在系统存在未知参数摄动和外界不确定性干扰的情况下，设计的控制器具有良好的跟踪性能，可以使得近空间可变翼飞行器稳定跟踪所给定高度和速度指令信号。

1) 考虑闭环系统的第1个子系统。

(10)

定义z1=x1-γd，其中，γd为航迹角参考指令，即ym=γd。对z1求导可得

(11)

引入虚拟控制量，即

(12)

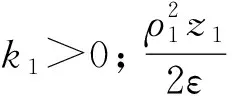
2) 考虑闭环系统的第2个子系统。

(13)

定义z2=x2-x2d，其中,x2d是虚拟控制量。对z2求导可得

(14)

引入虚拟控制量，即

(15)

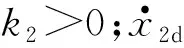
3) 考虑闭环系统的第3个子系统。

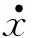
(16)

由式(16)可以看出，对于整个闭环系统的控制输入u进行设计。定义z3=x3-x3d，其中,x3d为虚拟控制信号。对z3求导可得

(17)

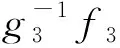
(18)

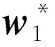
(19)

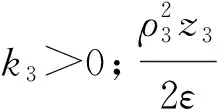
定义如下形式的矩阵W1,ψ

(20)

得到最终控制器输入为

(21)

(22)

式中：Γ1是正定阵；常数η>0。

2.2 速度控制器设计

对于速度子系统来说，油门开度主要影响速度控制。将速度改写为如下形式，即

(23)

式中，

(24)

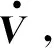
(25)

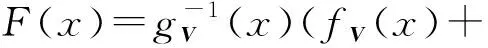
(26)

2.3 稳定性分析

定义滤波误差，滤波误差导数为

(27)

(28)

式中，B2和B3为连续函数，考虑如下Lyapunov函数

(29)

分别对V1,V2,V3求导得

(30)

(31)

3 数值仿真研究

针对上文建立的含有不确定性的近空间可变翼飞行器纵向模型，对高度为33 528 m、速度为4590 m /s的巡航段进行了数值仿真验证，平衡状态下攻角为2.745°、俯仰角速率为0(°)/s。为了说明基于Back-Stepping的鲁棒自适应动态面控制器具有较好的鲁棒性，将其与Back-Stepping设计的控制器做对比仿真验证研究。

加入内部参数摄动：升力比标称值减少30%，阻力比标称值增加30%。外部干扰： 加入10sint的速度测量误差，其高度和速度的跟踪响应曲线见图5、图6，控制器输出曲线见图7、图8。速度指令信号采用100 m/s、高度指令信号采用200 m的阶跃信号通过线性滤波给出，选取如下控制器参数：kH=0.1，k1=1，k2=4，k3=10，kV=10，ρ1=0.01，ρ3=0.04，τ1=τ2=0.01，η=0.01，δV=0.02，ε=0.01，Γ取单位矩阵，RBF网络初始权值先置为0，宽度取3。

图5 有无参数摄动时高度跟踪响应曲线Fig.5 Height tracking response curve with and without parameter perturbation

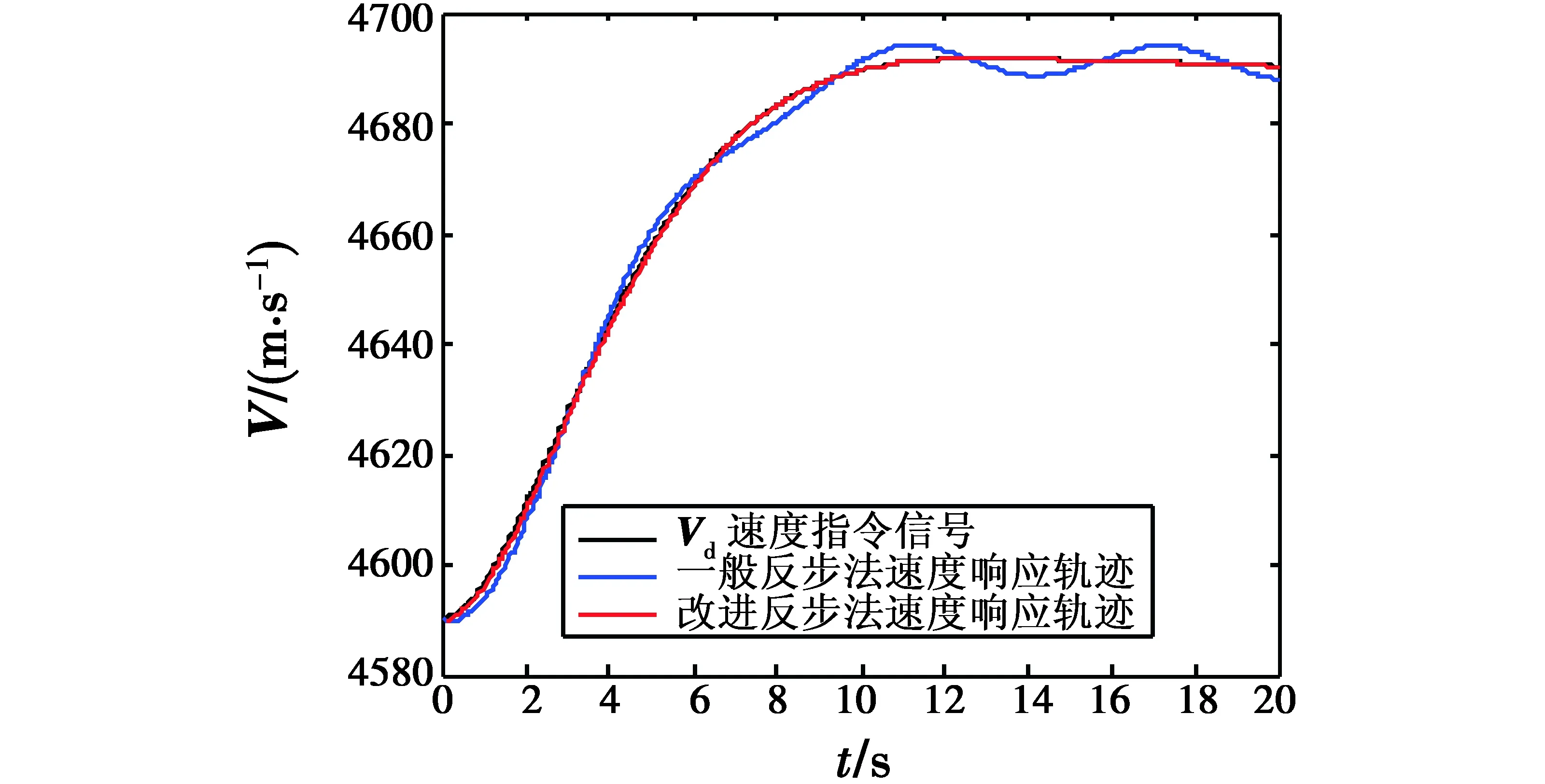
图6 有无参数摄动时速度跟踪响应曲线Fig.6 Velocity tracking response curve with and without parameter perturbation

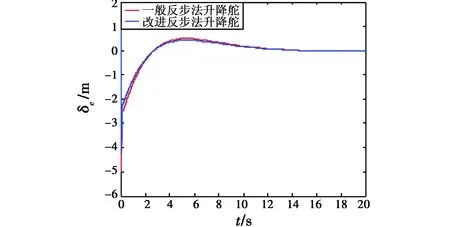
图7 有无参数摄动时的升降舵曲线Fig.7 Elevator curve with and without parameter perturbation

由仿真结果可以看出，当同时存在内部参数摄动和外部干扰的不确定性情况下，仅采用Back-Stepping设计的控制器不能达到理想的稳定跟踪控制效果，而RBF神经网络能有效逼近不确定性干扰对系统的影响，近空间可变翼飞行器能快速稳定地跟踪指令信号，说明基于Back-Stepping的鲁棒自适应动态面控制器具有较好的实时跟踪性和鲁棒性，对近空间可变翼飞行器能够达到较为满意的控制效果。

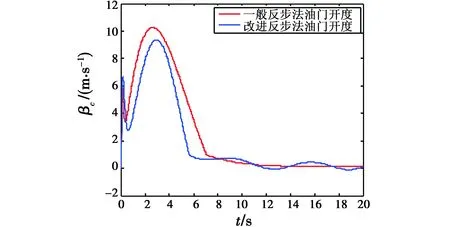
图8 有无参数摄动时的油门开度曲线Fig.8 Throttle opening curve with and without parameter perturbation

4 结论

本文针对具有高度非线性、气动参数不确定性、强耦合性的近空间可变翼飞行器等干扰问题，设计了基于Back-Stepping的鲁棒自适应动态面控制器。

控制器保留了Back-Stepping方法在处理非线性问题时的独特优越性，并采用RBF神经网络，补偿了反步法对参数不确定性、鲁棒性不足等缺点;本文加入了动态面控制思想，解决了多次微分导致的“微分膨胀”问题;通过Lyapunov函数和YOUNG氏不等式，分析证明了其稳定性;通过数值仿真验证结果表明，本文设计的鲁棒控制器对高度和速度具有良好的跟踪效果,解决了参数摄动和外部测量误差等干扰问题，说明该控制器具有较强的鲁棒性。