扭心偏移对桁梁桥颤振临界风速影响的试验研究

李永乐， 武 兵,2， 汪 斌， 唐 平

(1. 西南交通大学 桥梁工程系，成都 610031；2. 中铁第四勘察设计院集团有限公司，武汉 430063)

随着材料及技术的现代化发展，缆索承重体系桥梁跨度越来越大，同时其结构越来越轻柔，使得大跨度桥梁对风致作用越来越敏感。颤振作为风致动力稳定性能长期以来是大跨度桥梁抗风性能研究的重点，是大跨度桥梁设计的关键控制性因素[1-3]。桥梁颤振稳定性是一种复杂的空气动力学现象，其本质上受弹性力、惯性力、阻尼力和气动力的相互影响，通常由风洞试验进行研究与评价[4-6]。

因经济发展需要，山区大跨度桥梁在最近几年内得到较多的修建。在山区复杂地形环境中，因运输、施工方便，钢桁梁成为设计大跨度桥梁主梁的典型形式。借助于弹性节段模型试验，山区桁梁桥的颤振性能得到了较多的试验研究[7-11]。在弹性节段模型试验中，主梁扭转中心(扭心)通常取在节段模型的形心。实际上，大跨度缆索承重体系桥梁主梁的扭转受多种因素的影响，包括吊点位置、扭转振型、横向运动、竖向运动等因素，其扭心可能发生了偏移而不在截面形心位置。扭心的偏移使得风洞试验测试结果与实际情况可能存在一定偏差。

扭心偏移可能引起节段模型风洞试验中弹性转动中心、质量惯性矩、扭转频率的变化，从而进一步影响颤振临界风速。本文通过节段模型风洞试验模拟桁梁桥的扭心竖向偏移，测试实际大跨度斜拉桥与大跨度悬索桥的颤振临界风速，分析扭心偏移对颤振临界风速的可能影响。

1 试验方法

颤振临界风速测试采用常用的弹性节段模型系统，如图1所示。节段模型由四根刚度阻尼相同的弹簧悬挂在风洞中，弹簧及支撑系统放置在风洞壁面之外以避免对流场的干扰。弹簧提供所需要模拟的桥梁刚度，通过在弹簧上附加橡皮筋的方式可以增大系统阻尼。在水平方向上，通过细长钢丝限制模型的水平运动。在弹簧及限位钢丝作用下，节段模型具有竖向及扭转两个自由度。试验中需要在刚性水平支架左右两边对称布置铅块进行配重以满足质量相似，通过调整铅块的水平位置可以调整模型的质量惯性矩。在不同来流风速条件下，由激光位移计测试模型的竖向及扭转位移，获得颤振临界风速。

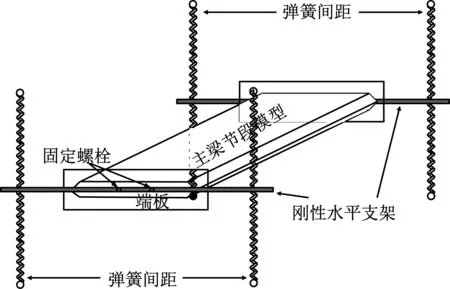
图1 弹性节段模型系统示意Fig.1 Schematic of sectional model with elastic support

模型扭心位于刚性水平支架中心，通常试验中假定扭心位于形心位置，直接将刚性水平支架固定在节段模型两端端板上，使得刚性支架转动中心与形心重合。通过调整刚性水平支架与模型的竖向相对位置，可以实现扭心的竖向偏移。如图2所示，模型端板沿着竖向不同位置开支架安装孔，通过螺栓将刚性水平支架固定在不同支架安装孔位置，从而实现支架与模型竖向相对位置的改变。

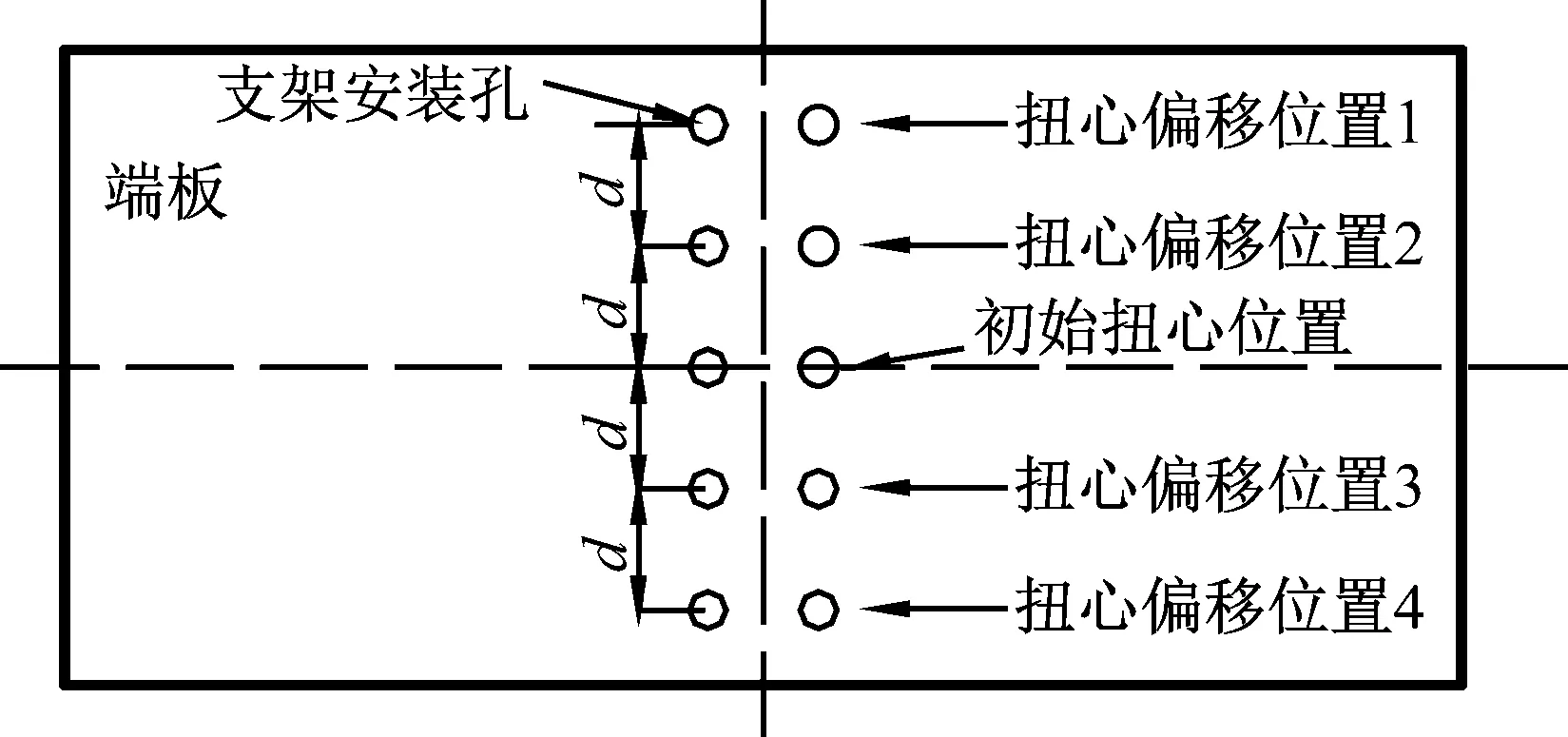
图2 模型端板安装孔示意Fig.2 Schematic of mounting holes on end plate

扭心偏移可能引起节段模型风洞试验中弹性转动中心、质量惯性矩、扭转频率的变化，为充分反映这三种因素的影响，对每一扭心偏移位置进行三组颤振临界风速测试：①试验一是在移动支架完成扭心偏移的同时调整配重的位置，使得系统扭弯频率比、质量惯性矩与要求值相等；②试验二是在移动支架完成扭心偏移的同时不调整配重的位置，通过调整同侧的弹簧间距使得系统扭弯频率比与要求值相等；③试验三则是在移动支架完成扭心偏移的同时既不调整配重的位置，也不调整弹簧间。通过试验一的不同扭心偏移位置的比较，可以反应扭心偏移引起的弹性转动中心变化对颤振临界风速的影响。试验二与试验一相比，相同扭心偏移下系统的弹性中心、扭转频率相同，但绕扭心的质量惯性矩改变。通过试验二与试验一的比较，可以反应在弹性中心、扭转频率相同情况下，扭心偏移引起的质量惯性矩变化对颤振临界风速的影响。与试验二相比，相同扭心偏移下试验三弹性转动中心、质量惯性矩相同，而扭转频率发生变化。通过试验三与试验二的比较，可以反应在弹性中心、扭转频率相同情况下，扭心偏移引起的扭转频率变化对颤振临界风速的影响。

2 大跨度斜拉桥颤振临界风速

某主跨532 m大跨度钢桁梁斜拉桥，主梁高12.5 m、宽36.2 m，竖弯基频0.169 Hz，扭转基频0.402 Hz，扭弯频率比2.377。按照《公路桥梁抗风设计规范》[12]，得到单位长度主梁等效质量与等效质量惯性矩分布为59.26 t/m，1.49×104t·m。满足几何相似性要求，按照1∶51.8缩尺比制作节段模型，如图3所示。在刚性水平支架上进行对称配重，满足质量相似性要求。试验中扭转阻尼比0.16%，竖弯阻尼比0.46%，风洞阻塞比小于5%。

图3 斜拉桥主梁节段模型Fig.3 Segmental model of girder of cable-stayed bridge

如第2节所述，在节段模型端板不同竖向位置开孔以调整不同的扭心偏移位置，端板开孔如图4所示。图5展示了刚性支架连接在扭心偏移位置时的试验情况，风致振动过程中主梁将绕着新的扭心位置(刚性水平支架中心)发生扭转运动。共测试了五种扭心位置的颤振性能。每个位置分别进行了α=0°，α=±3°三种攻角情况下的颤振临界风速测试。

图4 端板竖向开孔Fig.4 Vertical holes on end plate

图5 扭心偏移Fig.5 Offset of torsional center

2.1 弹性转动中心影响

如第2节所述，试验一扭心位置发生竖向偏移，同时调整系统配重位置，使得扭弯比与要求值近似相等，弹簧间距保持不变。不同扭心位置下节段模型系统扭弯比实现值如表1所示，模型系统扭弯比基本在要求值附近。以扭心无偏移扭弯比为基准，扭心偏移下最大扭弯比差别在0.4%以内。

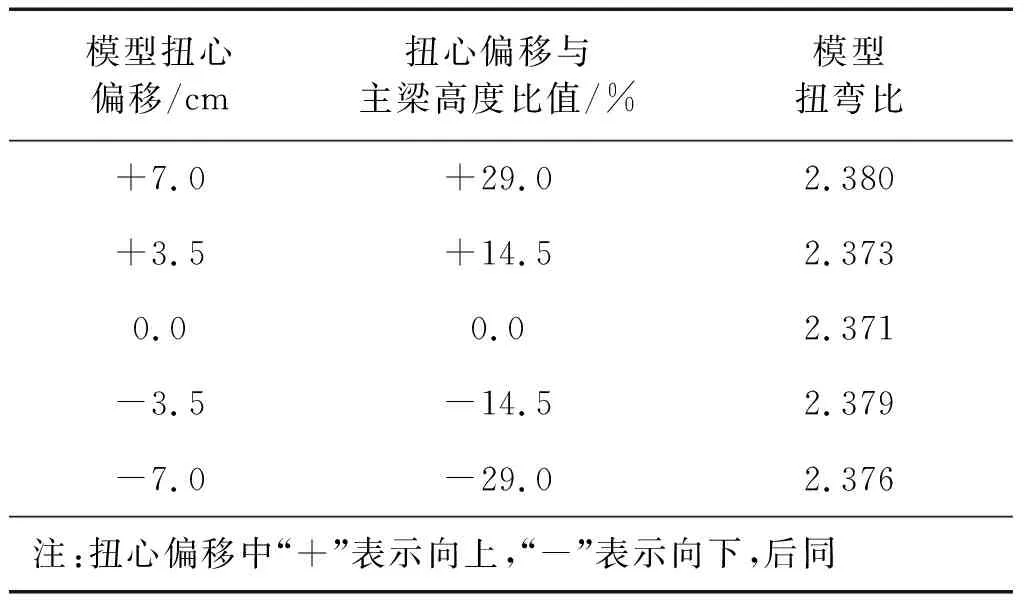
表1 试验一扭弯比(斜拉桥)Tab.1 Torsion-bending ratio in test I (cable-stayed bridge)

0°、±3°三种风攻角下测试得到的颤振临界风速如表2所示，不同风攻角下颤振临界风速均随着弹性转动中心偏离距离增大而变大。以不同风攻角下扭心无偏移颤振临界风速为标准，得到有无扭心偏移颤振临界风速比值(见表2)，可直观反映颤振临界风速改变程度。弹性转动中心向上偏移29.0%主梁高度时，颤振临界风速增大5.4%～11.4%；向下偏移29.0%主梁高度时，颤振临界风速增大5.6%～14.3%。

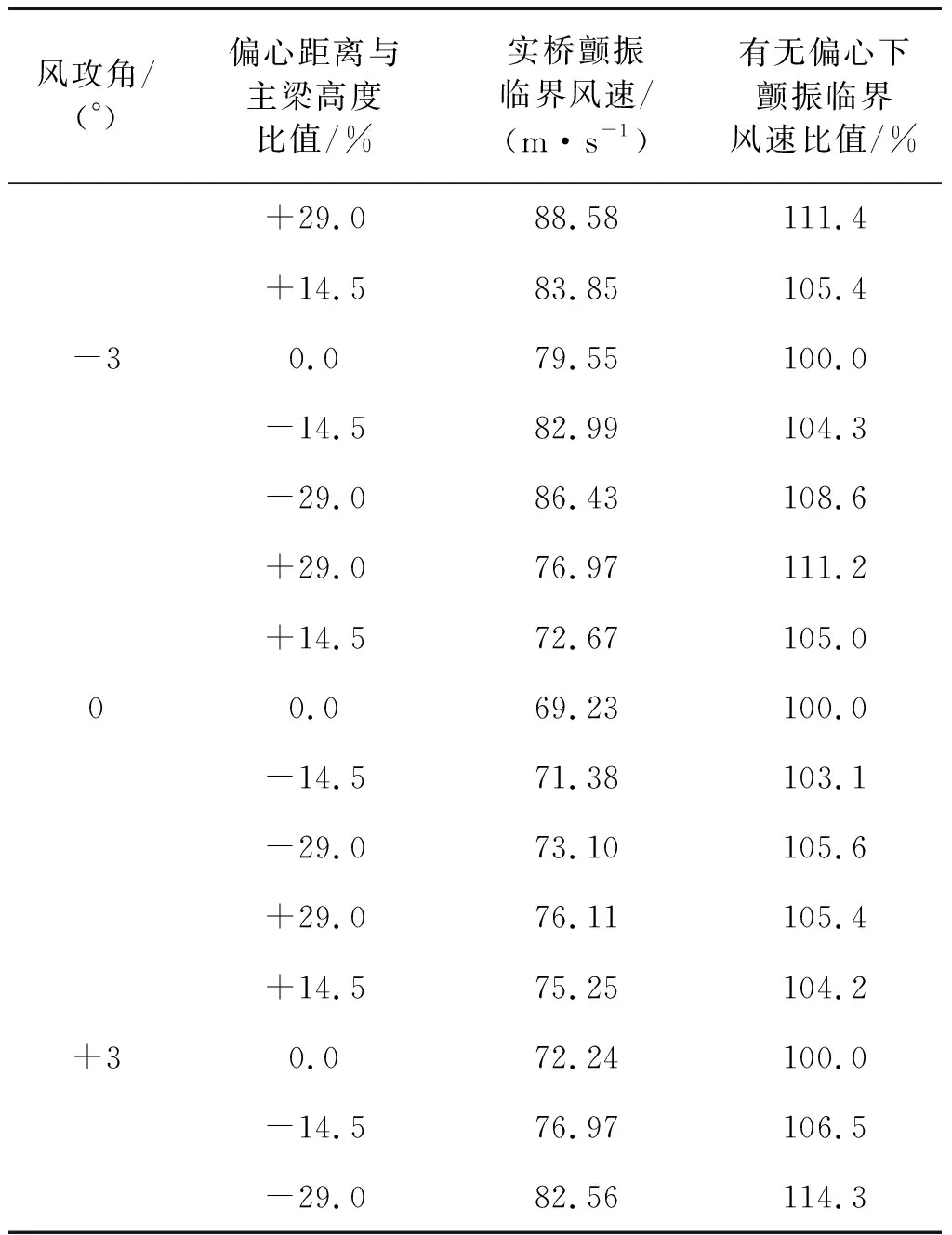
表2 试验一实桥颤振临界风速结果(斜拉桥)Tab.2 Flutter wind velocity in test I (cable-stayed bridge)

2.2 质量惯性矩影响

如第2节，试验二中扭心位置发生竖向偏移，不改变配重大小及位置，调整弹簧间距，使得扭弯比与要求值近似相等。节段模型弹性系统扭弯比实现值如表3所示，模型弹性系统扭弯比基本在要求值附近。以扭心无偏移扭弯比为基准，扭心偏移下最大扭弯比差别在0.5%以内。

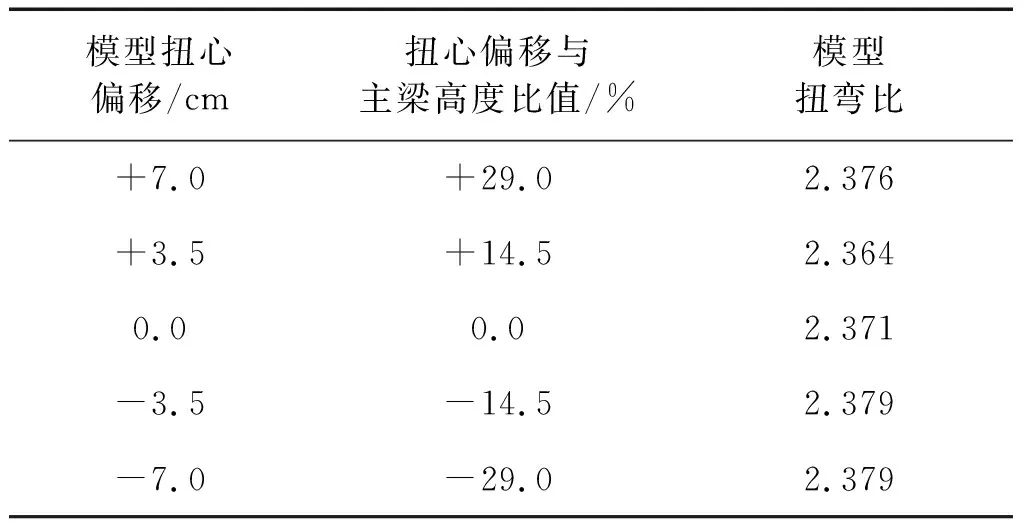
表3 试验二扭弯比(斜拉桥)Tab.3 Torsion-bending ratio in test II (cable-stayed bridge)

不同风攻角下试验一与试验二有无扭心偏移颤振临界风速比值比较如图6所示。试验二与试验一相比，质量惯性矩存在差异。扭心向下偏移情况下，质量惯性矩对颤振临界风速的影响不大。扭心向上偏移时，质量惯性矩对颤振临界风速的影响与风攻角有关。在0°风攻角下影响大，向上偏移量29%主梁高度时颤振临界风速比值相差7.5%。尽管部分工况下颤振临界风速较试验一有所降低，但是仍高于无扭心偏移条件的颤振临界风速。

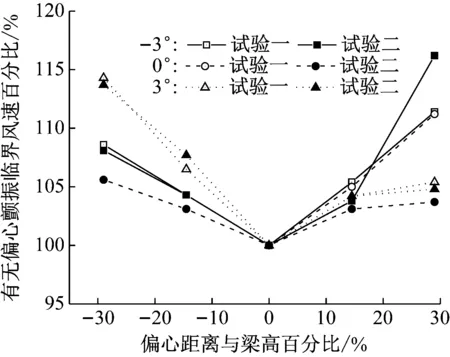
图6 试验一、二颤振临界风速比值比较(斜拉桥)Fig.6 Comparison of ratio of flutter wind velocity in tests I and II (cable-stayed bridge)

2.3 扭转频率影响

如第2节，试验三中扭心位置发生竖向偏移，不调整系统配重大小及位置，也不调整弹簧间距。节段模型弹性系统扭弯比实现值如表4所示，扭弯比随扭心偏移距离增大而变小。扭心上偏距离为主梁高度29%时，模型扭弯比最大降低了3.2%。可知，随着扭心偏移距离的增加，扭转频率降低。

不同风攻角下试验二与试验三有无扭心偏移颤振临界风速比值比较如图7所示。试验三与试验二相比，扭转频率存在差异。扭转频率对颤振临界风速比值的影响与风攻角有关，整体上-3°风攻角下影响不大。在0°，3°风攻角下比值改变较为明显：扭心向上偏移时，扭转频率降低导致颤振临界风速增大；扭心向下偏移时，扭转频率降低导致颤振临界风速减小；改变幅度随着偏移距离增大而增大，最大改变5.7%。同样，扭心偏移条件下颤振临界风速高于无扭心偏移条件的颤振临界风速。

3 大跨度悬索桥颤振临界风速

某主跨1 100 m大跨度钢桁梁悬索桥，主梁高8.2 m、宽27.0 m，竖弯基频0.149 Hz，扭转基频0.307 Hz，扭弯频率比2.060。按照《公路桥梁抗风设计规范》，得到单位长度主梁等效质量与等效质量惯性矩分布为36.43 t/m，4.25×104t·m。满足几何相似性要求，按照1∶43.63缩尺比制作节段模型，如图8所示。在模型刚性水平支架上进行对称配重，满足质量相似性要求。试验中扭转阻尼比0.23%，竖弯频率比0.48%，风洞阻塞比小于5%。端板开孔如图9所示，不同竖向位置开孔用以调整扭心偏移位置。类似于斜拉桥，五种扭转中心位置下对颤振临界风速进行了测试，分别考虑了α=0°，α=±3°三种风攻角情况。

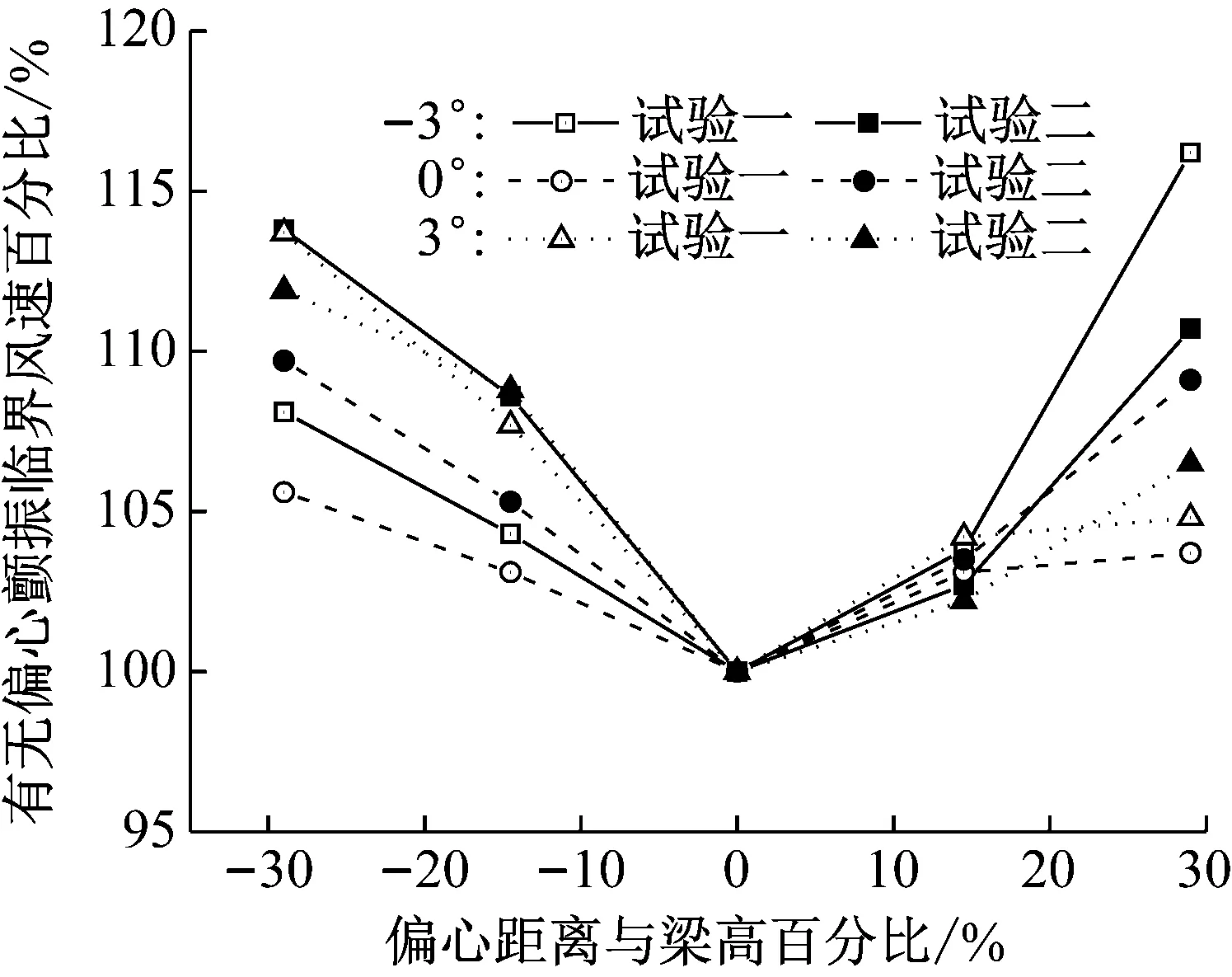
图7 试验二、三颤振临界风速比值比较(斜拉桥)Fig.7 Comparison of ratio of flutter wind velocity in tests II and III (cable-stayed bridge)

图8 悬索桥主梁节段模型Fig.8 Segmental model of girder of suspension bridge

图9 端板竖向开孔Fig.9 Vertical holes on end plate

3.1 弹性扭转中心影响

试验一中扭心位置发生竖向偏移引起弹性扭转中心发生变化。节段模型系统扭弯比实现值如表5所示，模型系统扭弯比基本在要求值附近。相比于无扭心偏移条件，扭弯比最大相对差别为0.1%。0°、±3°三种风攻下测试得到的实桥颤振临界风速如表6所示，不同风攻角下颤振临界风速随着弹性扭转中心偏离距离增大而变大。弹性扭转中心向上偏移35.1%主梁高度时，颤振临界风速增大4.0%～24.9%。向下偏移35.1%主梁高度时，颤振临界风速增大3.9%～8.4%。

表5 试验一扭弯比(悬索桥)Tab.5 Torsion-bending ratio in test I (suspension bridge)

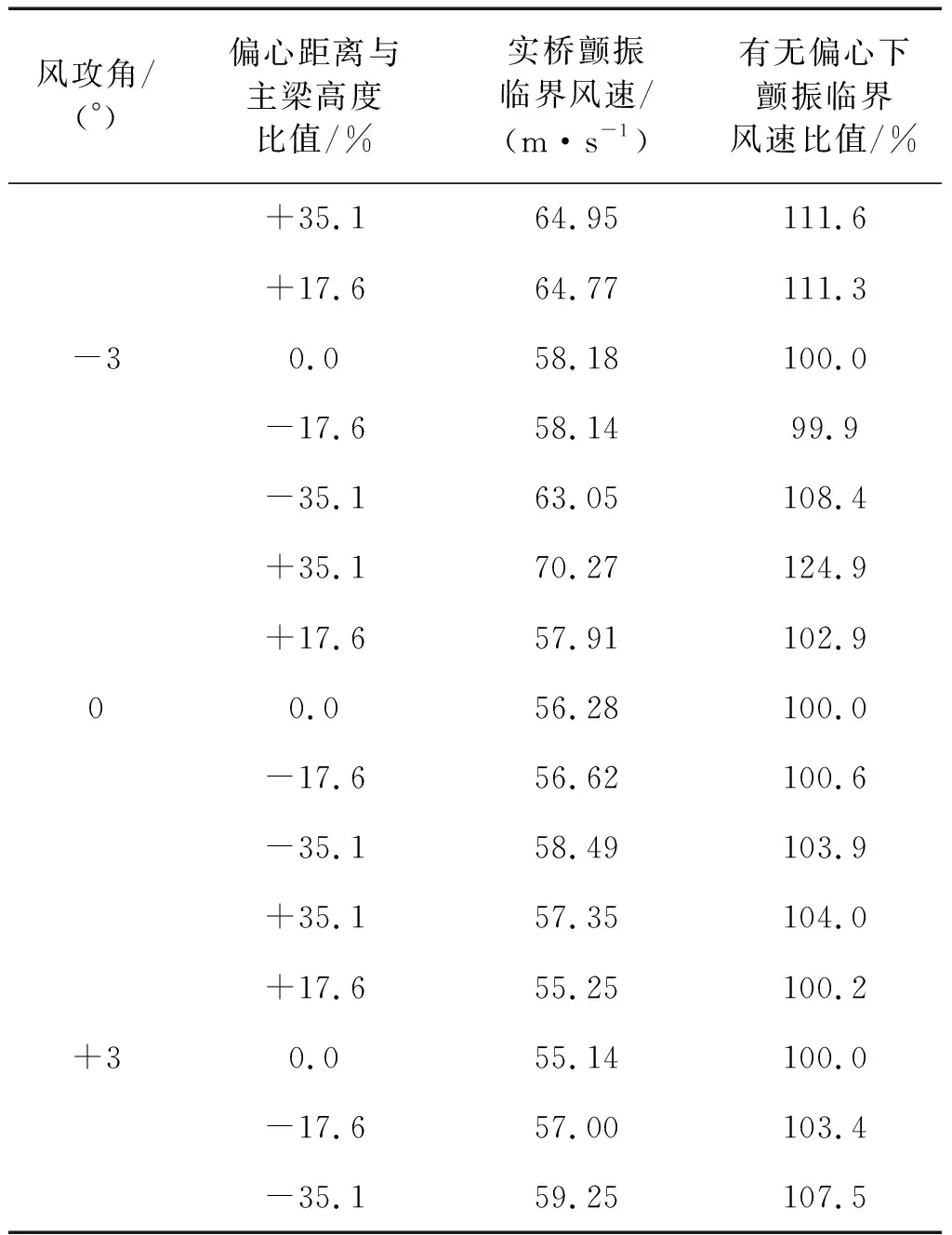
表6 试验一实桥颤振临界结果(悬索桥)Tab.6 Flutter wind velocity in test I (suspension bridge)

3.2 质量惯性矩影响

在相同扭心偏移位置下，试验二的弹性中心、扭转频率与试验一相同，质量惯性矩改变。试验二中节段模型弹性系统扭弯比实现值如表7所示，基本在要求值附近。相比于无扭心偏移情况，扭弯比最大相对差异为0.2%。试验一与试验二颤振临界风速比值比较如图10所示，质量惯性矩对颤振临界风速的影响与风攻角有关。扭心向上偏移35.1%主梁高度时，颤振临界风速比值最大相差2.7%；向下偏移量29%主梁高度时，颤振临界风速最大相差6.1%。扭心偏移条件下颤振临界风速高于无偏移条件。

表7 试验二扭弯比(悬索桥)Tab.7 Torsion-bending ratio in test II (suspension bridge)

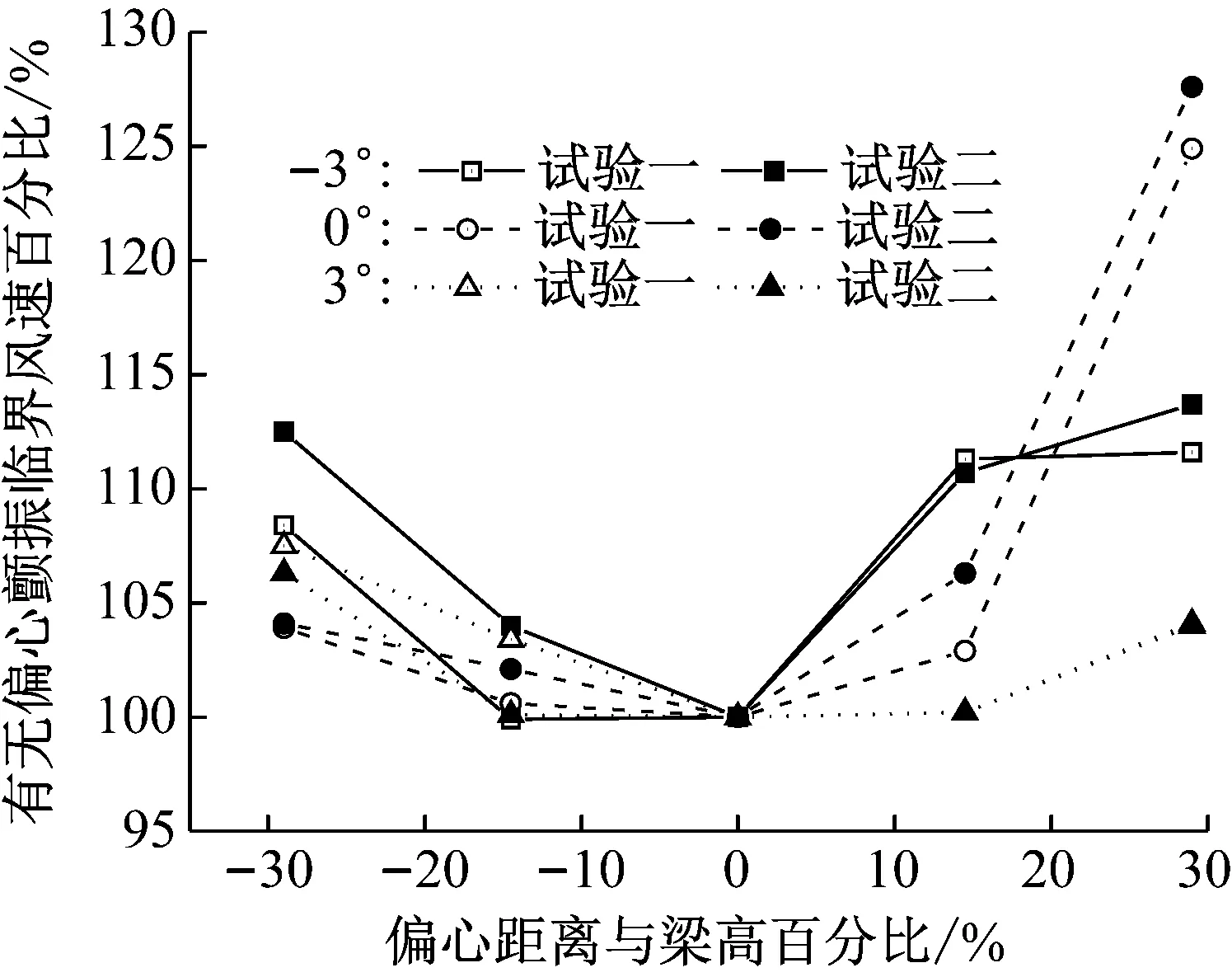
图10 试验一、二颤振临界风速比值比较(悬索桥)Fig.10 Comparison of ratio of flutter wind velocity in tests I and II (suspension bridge)

3.3 扭转频率影响

相比于实验二，试验三扭转频率发生变化。节段模型弹性系统扭弯比实现值如表8所示，模型弹性系统扭弯比随偏移距离增大而变小。扭心下偏距离为主梁高度35.1%时，模型扭弯比降低最大为2.8%。不同风攻角下试验二与试验三颤振临界风速比值比较如图11所示，扭转频率对颤振临界风速增的影响与风攻角有关，改变幅度整体上随着偏移距离增大而增大。扭心向上偏移时扭转频率降低导致颤振临界风速增大可达11.5%；向下偏移时扭转频率降低导致颤振临界风速减小可达6.2%。扭心偏移条件下颤振临界风速依然高于无偏移条件。

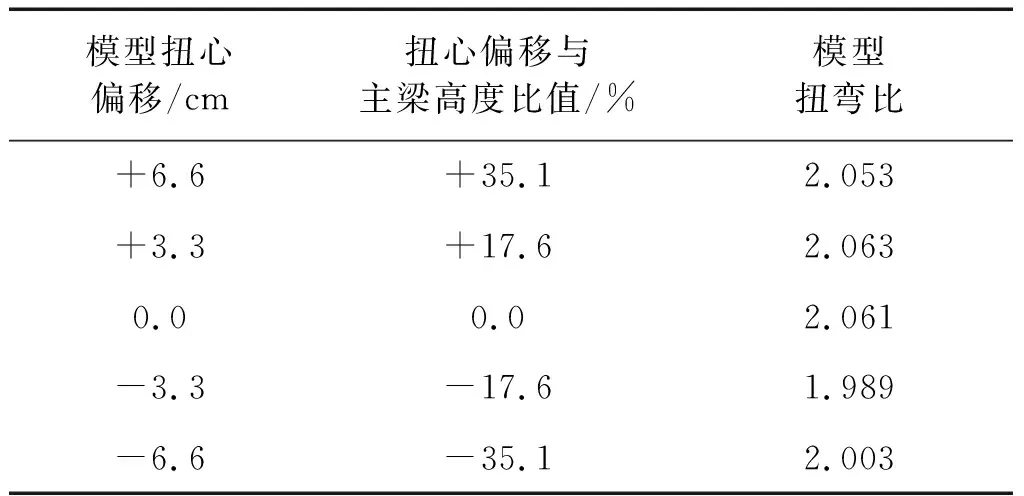
表8 试验一扭弯比(悬索桥)Tab.8 Torsion-bending ratio in test I (suspension bridge)

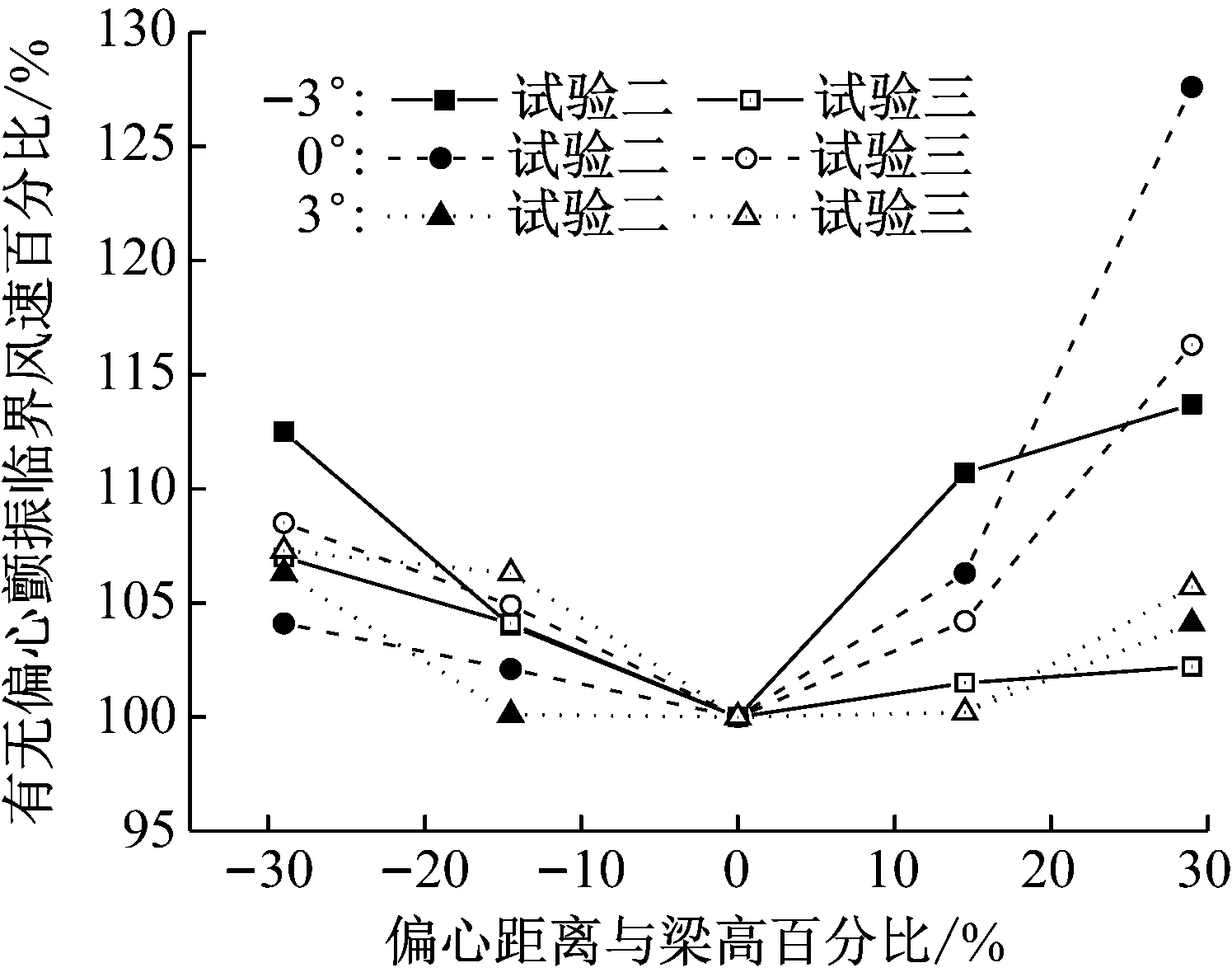
图11 试验二、三颤振临界风速比值比较(悬索桥)Fig.11 Comparison of ratio of flutter wind velocity in tests II and III(suspension bridge)

4 结 论

本文通过节段模型风洞试验模拟桁梁桥的扭心偏移，对比研究弹性转动中心、质量惯性矩、扭转频率作用，针对0°、±3°三种风攻角下大跨度斜拉桥与悬索桥分析扭心偏移对颤振临界风速的可能影响，主要结论有：

(1) 总体上，扭心偏离形心使得桁梁桥颤振临界风速提高。节段模型试验中将扭心设在桁梁桥模型端板中心可以获得较为保守的颤振临界风速。

(2) 三种风攻角下，颤振临界风速均随着扭心偏移引起的弹性转动中心偏离距离增大而变大。对于所选择斜拉桥，偏离主梁29.0%高度时，颤振临界风速增大在5.4%～14.3%。对于所选择悬索桥，偏离主梁35.1%高度时，颤振临界风速增大在3.9%～24.9%。

(3) 扭心偏移引起的质量惯性矩变化对颤振临界风速的影响与风攻角有关。对于所选择斜拉桥，偏离主梁29.0%高度时，颤振临界风速差异最大为7.5%。对于所选择悬索桥，偏离主梁35.1%高度时，颤振临界风速差异最大为6.1%。

(4) 扭心偏移引起的扭转频率变化对颤振临界风速的影响也与风攻角有关。对于所选择斜拉桥，改变幅度最大为5.7%。对于所选择悬索桥，改变幅度可达11.5%。