脉冲燃烧风洞测力系统传力特性研究
2018-11-21李世超高宏力刘勃锴付国强鲁采江
李世超, 高宏力, 刘勃锴, 付国强, 鲁采江
(西南交通大学 机械工程学院,成都 610000)
飞行器研发过程中需进行风洞测力试验,以了解其气动特性[1-5]。测试精度不但影响飞行器的研制风险与成本,而且还制约其气动特性的评估与优化。脉冲燃烧风洞是用于揭示高超声速飞行器气动特性的地面试验设备[6-8],作用于飞行器模型表面的气动力与力矩由测力系统中的天平测量。由于飞行器模型所受的气动力要经过测力系统内部结构才能传递至天平上,因此测力系统的传力特性会直接影响气动力的测试精度[9]。
目前关于风洞测力系统测试精度的研究主要集中在以下几个方面:新型测试原理的探索;惯性力补偿技术研究;振动控制技术研究;在测试原理的研究方面,Sanderson等[10]基于应力波的传递原理,设计了一种应力波天平;罗也凡等[11]提出了一种能进行惯性力补偿的加速度计应变天平;在惯性力补偿方面,Bernstein等[12]通过在飞行器模型的适当位置安装加速度传感器来获取其在试验过程中因振动引起的惯性力,在此基础上,对天平输出信号进行补偿;在振动控制方面,Capone等[13]采用被动减振技术,通过在测力系统的适当位置加装阻尼元件,以降低飞行器模型的振动幅度;陈卫东等[14]基于主动减振技术,将激振器安装在飞行器模型空腔内合适位置,并基于各种控制算法,通过控制激振器的输出来达到降低飞行器模型振动幅度的目的;以上文献均是针对改善测力系统的测试精度进行研究,然而关于测力系统传力特性的评估却鲜见报道。
本文提出了一种基于有限元仿真来评估测力系统传力特性的方法。首先,通过参数辨识得到了各零部件材料属性真实值,以此为基础,建立了测力系统有限元模型,并对整机进行模态试验,验证了该有限元模型的准确性;其次,基于飞行动力学相关理论得出了飞行器模型重心与天平之间的传力特性可以反映测力系统整机传力特性的结论;对测力系统有限元模型进行谐响应分析,并提取天平中应变计粘贴处的位移幅频曲线,结合位移幅频曲线与天平测力公式获得激励力在飞行器模型重心与天平浮动框间的传递幅频特性曲线;最后,将作用于飞行器表面的气动力等效为飞行器模型重心处的集中力(激励力),并基于傅里叶变换展开成一系列谐波力信号,通过幅频特性曲线计算出各谐波力传递至天平浮动框后的大小,以此为基础,结合天平最低测试分辨率筛选出未被天平识别的谐波力信号,并计算未被识别的谐波力信号总能量占激励力信号总能量的百分比,以此来评价测力系统传力特性的优劣。
1 概 述
本文以某脉冲燃烧风洞测力系统为研究对象,其结构如图1所示,由高超声速飞行器模型、测力天平和支架三部分组成,天平浮动框与飞行器模型间采用螺钉固连,天平固定框与支架之间同样采用螺钉紧固的方式连接。其中测力天平为盒式六分量应变天平,其结构简图如图2所示,由浮动框、固定框和弹性测量元件组成,弹性测量元件将浮动框和固定框连接成一整体。工作时风洞产生的气流作用在飞行器模型上产生气动力,使得天平浮动框与固定框发生相对位移,粘贴于测量元件上的箔式应变计产生形变,从而导致电阻发生变化,惠斯通电桥将电阻的变化转变为电压输出,此即测力系统的测试原理,图3展示了箔式应变计A1~A10在天平中的安装位置。

1-飞行器模型;2-应变天平;3-支架图1 测力系统结构简图Fig.1 Measuring system structure diagram

图2 应变天平结构简图Fig.2 Strain balance structure diagram

图3 天平箔式应变计粘贴位置Fig.3 Foil strain gauge paste position
2 测力系统有限元模型的建立
2.1 测力系统几何模型简化
进行测力系统有限元建模时,由于系统中包含诸多圆角,倒角和孔等微小结构,它们对整机动态特性影响小,然而模型在进行有限元网格划分时这些结构会明显增加网格数量,增大计算量,因此,在保证有限元模型精度的前提下对整机模型进行合理的简化能有效降低计算成本,提高计算效率,测力系统简化原则如下:
(1) 忽略结构中的小倒角和圆角;
(2) 删除结构中的小定位孔及螺纹孔等细小特征。
简化后的模型如图4所示。
2.2 测力系统有限元建模
测力系统是由各零部件通过结合部连接而成的装配体。其中结合部指的是零部件间相互接触并能传递力的部分,研究表明,装配体整体刚度与阻尼的60%和90%以上由结合部贡献[15],因此结合部动态特性对整机动态特性有重要影响,在测力系统动力学建模时须正确描述结合部动态特性。因此,测力系统整机有限元建模包括各零部件有限元建模和结合部有限元建模,有限元建模采用Ansys软件实现。

图4 测力系统简化模型Fig.4 Force measurement system simplified model
2.2.1 单一零部件建模
测力系统中的主要零部件包括飞行器模型,天平与支架,采用20节点的solid186单元和10节点的solid187单元分别对飞行器模型,天平和支架进行网格划分, 共得到88 455个单元,181 626个节点。在建模过程中需要赋予各零部件相应的材料属性,要想建立准确的各零部件有限元模型,需赋予有限元模型正确的材料属性,然而各零部件材料属性的参考值与真实值间存在一定的差异,因此,为了提高各零部件有限元模型的精度,需对零部件的材料属性进行辨识。本文基于优化思想分别对飞行器模型与天平的弹性模量,密度,泊松比真实值进行辨识。
2.2.1.1 零部件材料属性辨识
基于优化算法的材料属性辨识思想为:采用优化策略不断调整有限元模型中的材料属性值,最小化零部件有限元模型前N阶理论模态与前N阶试验模态间的综合误差,直至误差小于收敛值ε时,即可认为此时有限元模型中的材料属性值即为零部件材料属性的真实值。
基于该辨识思想,具体的参数辨识流程描述如下:

式中:N为模态阶数;ε为优化截止条件。
(2) 在MATLAB中编写能与Ansys进行相互调用的优化程序,该程序基于鲍威尔优化理论,能够实现单一目标函数、多变量的优化。首先,通过MATLAB调用Ansys进行模态分析并提取前四阶模态频率,基于Ansys的APDL语言将计算获得的前四阶模态频率反馈到MATLAB中,通过优化算法,MATLAB将优化后各零部件弹性模量、泊松比与密度值传递给Ansys,以此流程自动循环迭代直至达到优化终止条件,输出最终材料属性值。
2.2.1.2 零部件模态试验
在零部件参数辨识过程中需要各零部件的前N阶试验模态,本文采用单点激励,多点响应数据采集(Single Input Multiple Output, SIMO)方式分别对零部件进行锤击模态试验。飞行器模型与天平均采用自由悬挂的方式,近似模拟零件自由状态,各零部件上力锤激励点和加速度测点的位置如图5和图6所示,试验设备包括北京东方所的数据采集系统,力锤与三向压电式加速度传感器。

图5 飞行器模型测点与激励点的位置分布Fig.5 Distribution of locations of measurement points and excitation points in aircraft models

图6 天平测点与激励点的位置分布Fig.6 Distribution of locations of measurement points and excitation points in strain balance
2.2.1.3 零部件有限元模型验证
经过参数辨识后,辨识得到的各零部件材料属性值列于表1。对比各零部件参数辨识后的计算模态频率与试验模态频率如表2所示,从表2可以发现,参数辨识后各零部件的计算模态值与试验模态值间的最大误差分别为8.5%与9.6%,其余误差均在5%内,由此表明所建立的零部件有限元模型能准确描述其动力学特性。

表1 零部件参数辨识值Tab.1 Parameter identification value of parts

表2 参数辨识后零部件理论模态值与试验模态值对比Tab.2 Comparison of theoretical modal values and experimental modal values of component parts after parameter identification
2.2.2 结合部建模
测力系统中的主要结合部包括飞行器模型-天平螺钉固定结合部与天平-支架螺钉固定结合部,由于结合部表现出既存储能量又释放能量的特性[16],因此采用弹簧-阻尼模型来描述结合部动态特性,对系统动态特性影响较小的结合部在Ansys中采用黏接处理。在螺钉固定结合部上的每个螺钉位置处用一个法向弹簧-阻尼单元和两个切向弹簧-阻尼单元模拟,螺钉固定结合部弹簧-阻尼模型如图7所示,其中圆圈代表弹簧-阻尼单元的位置,它与螺钉的中心轴位置重合。

图7 结合部弹簧阻尼模型Fig.7 Spring damping model of joint
其中弹簧-阻尼单元的刚度系数与阻尼系数通过计算获得,具体流程如下:
步骤1运用吉村允效法[17]获得结合面上单位面积的刚度系数与阻尼系数;
步骤2对结合面上单位面积刚度系数与阻尼系数积分,求得结合面的总体刚度系数和阻尼系数;
步骤3将总体刚度系数与阻尼系数均分至每个弹簧-阻尼单元从而获得每个弹簧-阻尼单元的刚度系数和阻尼系数;
步骤2中结合面总刚度系数和总阻尼系数的计算公式为
(1)
(2)
(3)
(4)
式中:Pn为结合部面压;kn(Pn),kt(Pn),cn(Pn),ct(Pn)分别为结合面单位接触面积的法向刚度、阻尼系数和切向刚度、阻尼系数;Kn,Cn,Kt,Ct为结合面的总体法向刚度、总体法向阻尼系数、总体切向刚度、总体切向阻尼系数。结合部面压可由式(5)、式(6)计算。
(5)
(6)
式中:Pn为结合面面压;d2为螺纹中径;φ为螺纹升角;ρv为螺纹当量摩擦角;μ为螺母与被连接件支撑面间的摩擦因数;T为螺钉的预紧力矩;Dw为六角螺母直径;d0为螺钉中径。
以测力系统中的飞行器模型-天平螺钉固定结合部、天平-支架螺钉固定结合部为例,阐述其弹簧-阻尼单元的刚度系数和阻尼系数的具体计算过程:首先由式(5)式(6)计算出飞行器模型-天平螺钉固定结合部、天平-支架螺钉固定结合部的接触面压分别为8.95 MPa,2.4 MPa。基于结合部面压和结合面表面粗糙度,通过查询文献[18]得到结合面单位接触面积的刚度与阻尼系数,如表3所示,以上结合部中结合面的粗糙度均为3.2 μm。再根据式(1)~式(4)求出结合面总体刚度系数和阻尼系数。最后,将结合部整体刚度系数与阻尼系数均分至该结合部上的所有弹簧-阻尼单元,从而获得单个弹簧阻尼单元的刚度系数和阻尼系数如表4所示。
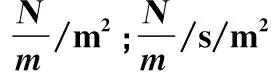
表3 结合部单位面积接触刚度与阻尼Tab.3 The contact stiffness and damping of unit area

表4 弹簧-阻尼单元刚度系数与阻尼系数Tab.4 The stiffness coefficient and damping coefficient in spring-damping element
2.2.3 整机有限元模型验证
将结合部弹簧-阻尼模型与零部件有限元模型综合成测力系统整机有限元模型,其中,支架底面采用完全固定约束,如图8所示。为验证模型的准确性,对测力系统进行整机模态试验,对比试验模态频率与计算模态频率如表5所示,其中计算模态值与试验模态值间的最大误差为10.3%,其余误差均在10%内,证明测力系统整机有限元模型能准确描述其动态特性。
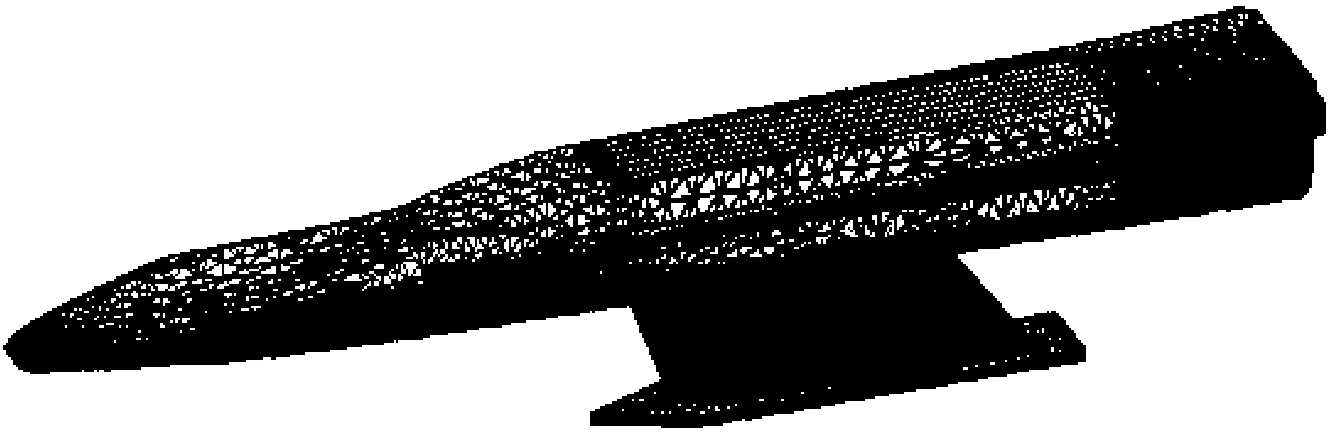
图8 测力系统整机有限元模型Fig.8 Finite element model of the force measuring system

表5 模型验证Tab.5 Model validation
3 天平标定
天平测力公式是传力特性分析的基础,在Ansys中采用虚拟静态校准方法,获得天平输入与输出之间的关系,天平测力公式为
(7)
式中:Fx,Fy,Fz,Mx,My,Mz分别为作用于天平浮动框沿x,y,z方向的轴向力与转矩;εn,x,εn,y,εn,z分别为编号为n的箔式应变计在x,y,z方向上的位移;kn,n为天平静校矩阵中的系数。
采用表6所示的校准方案,校准力的加载位置为浮动框上表面,如图9所示,静校过程中每次加载只施加一种类型的力,其余力均为零,提取每次加载后所有箔式应变计粘贴处x,y,z三个方向上的位移,将每次校准过程中的校准力向量与箔式应变计的位移向量带入到式(7)中,可得标定矩阵中的一列,重复此过程,直至获得标定矩阵中所有系数为止。
为验证天平测力公式的准确性,在天平浮动框上表面同时施加表7所列的6种力,对比真实载荷与辨识载荷如表8所示,误差几乎为零,由此表明,天平测力公式精度完全满足要求。

图9 天平校准力加载位置Fig.9 The position of balance calibration loading
表6 天平校准方案Tab.6 The calibration program of balance

表7 天平测力公式精度验证施力方案Tab.7 The force scheme of accuracy verification of balance force formula

表8 天平测力公式验证Tab.8 Accuracy verification of balance force formula
4 测力系统传力特性分析
在风洞测力试验中,飞行器模型受到的气动力需要经过测力系统内部结构才能传递至天平上,因此测力系统传力特性的优劣性将直接影响其测试精度,为了保障测力数据的可信度,需要对测力系统的传力特性进行分析与评价。
天平对力的测量有分辨率限制,当作用于天平上的力低于其分辨率时,天平将无信号输出,此力便未能测得,本文中的应变天平分辨率为2 N,以此作为测力系统传力特性的判断依据,传力特性分析流程大致如下,流程图如图10所示:
1) 选取能反映测力系统整机传力特性的传力路径;
2) 基于有限元模型进行谐响应分析,提取激振力F(ω)作用于传力路径输入点时天平中所有应变计粘贴处的位移幅频特性曲线X1(ω),X2(ω),…,Xn(ω),其中n表示应变计编号;
3) 将应变计粘贴处位移幅频特性曲线X1(ω),X2(ω),…,Xn(ω)代入天平测力式(7)中,求出激振力F(ω)传递至天平浮动框后的力幅频特性曲线F′(ω);
4) 结合激振力幅频特性曲线F(ω)及激振力传递至天平浮动框后的力幅频特性曲线F′(ω),获得力在传力路径输入点与天平浮动框间的传递特性,计算公式如(8)所示;
5) 将作用于飞行器表面的气动力等效成集中力F并施加于传力路径的输入点;
6) 基于傅里叶变换将力F展开成一系列谐波信号并代入到传递函数式(8)计算出气动力F的各谐波力信号从传力路径的输入点传递至天平浮动框后的大小,傅里叶变换的展开公式如式(9)所示;
7) 以天平分辨率为依据筛选出为被识别的谐波力信号;
8) 计算未被识别的谐波力信号的能量E′占输入力信号总能量E的百分比ε,ε的大小可以反映测力系统的传力特性,计算公式如式(10)所示,能量E与E′的计算公式如式(11)与式(12)所示
(8)
(9)
(10)

(11)
(12)
式中:E为原始信号的总能量;F(ω)为激励信号傅里叶变换展开后频率为ω的谐波力信号的幅值;Δω为各谐波力信号频率间的差值;E′为未被天平识别的谐波力信号所占的能量;ωn表示第n个未识别的谐波力信号的频率;N为未识别的谐波力信号的总个数。

图10 传力特性分析流程图Fig.10 The flow chart of force characteristics analysis
4.1 传递路径的选择
本文中的力传递路径指的是气动力在测力系统中任意两点之间传递的路径,然而气动力是以面力的形式作用在飞行器模型上的,因此气动力在测力系统中的传递路径有无数多条,需从中找出一条传递路径能够描述整机的传力特性。由于测力系统所测得力指的是飞行器模型重心处的集中力,这是因为做飞行器飞行动力学分析时需要将其看成是刚体,并将面力形式的气动力等效成作用在飞行器重心处的集中力,所以,风洞测力试验的目的是给出飞行器模型在各种飞行条件下其重心处所受的集中力,基于此在设计时给予了飞行器模型较高的刚度,尽量让其传力特性接近于刚体的传力特性,所以,飞行器模型上任意一点至天平的传力特性可以等效成飞行器模型重心处到天平的传力特性,因此选用飞行器模型重心处与天平间的传力特性来描述测力系统整机传力特性。通过计算,飞行器模型重心在笛卡尔坐标系中的位置如表9所示。

表9 飞行器模型重心位置坐标Tab.9 The center of gravity location about aircraft model
4.2 测力系统谐响应分析
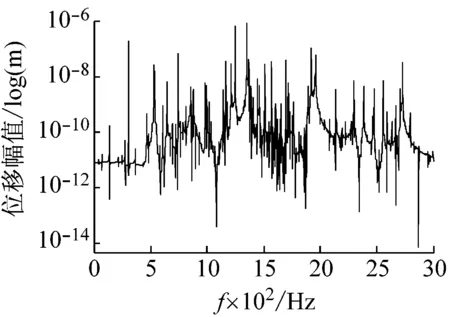
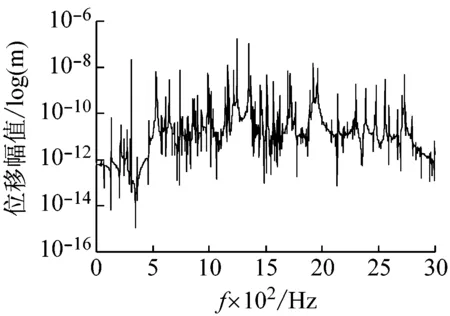
为了分析飞行器模型重心处与天平浮动框表面间的传力特性,首先需要获得激振力作用在飞行器模型重心处时,天平各应变计处的位移幅频响应曲线,因此对其进行谐响应分析。由于飞行器模型的重心并不在飞行器上,因此将重心沿x,y,z方向投影至飞行器模型上,如图11中的a,b,c三点。分别在此三点处施加幅值为1 000 N、激振频率为0~3 000 Hz的简谐力,其中a点施加x方向的激振力,b点施加y方向的激振力,c点施加z方向上的激振力,由于篇幅的限制这里只展示天平中编号为a1的箔式应变计粘贴处在x,y,z方向上的位移幅频特性曲线,如图12所示。
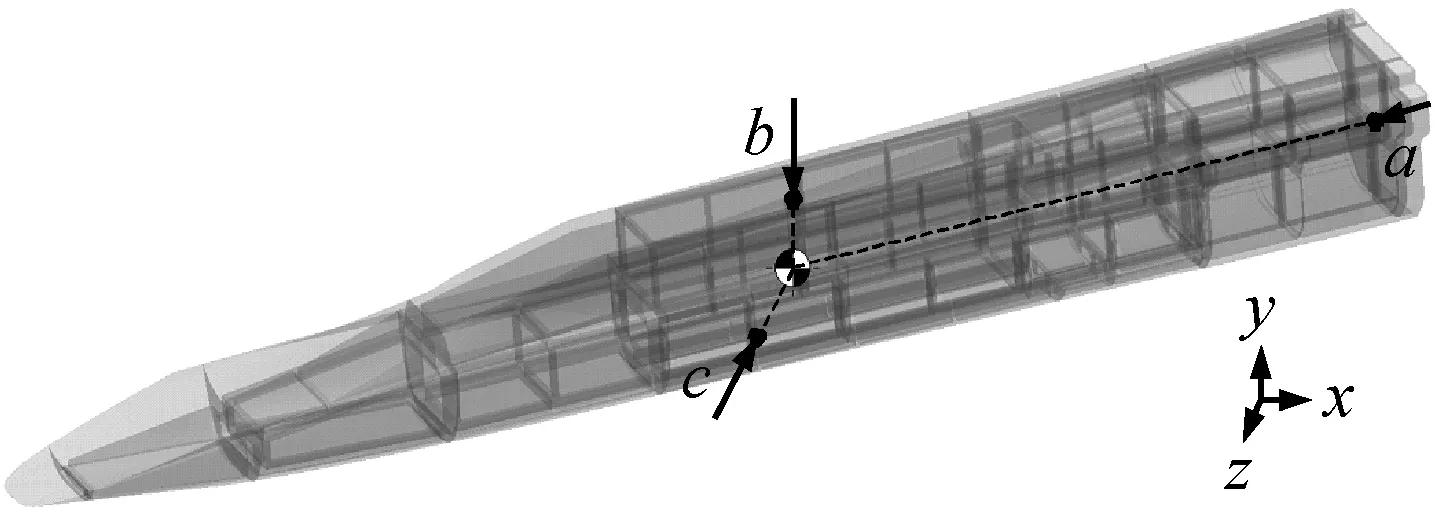
图11 激振力在飞行器模型上的投影Fig.11 Exciting force projection on aircraft model
(a) x方向的位移幅频特性曲线
(b) y方向的位移幅频特性曲线

(c) z方向的位移幅频特性曲线图12 应变片a1在x,y,z方向的位移幅频特性曲线Fig.12 The displacement amplitude-frequency characteristic curve of a1 in x, y, z direction
4.3 测力系统轴向传力特性
通过谐响应分析得到了激振力在a点沿x方向激振时各应变计粘贴处位移幅频特性曲线,分别将该曲线中各频率成分的幅值除以与之频率相对应的激振力幅值,得到单位激振力作用下的位移幅频特性曲线,并将其带入到天平测力式(7)中进行计算,得到作用在a点的单位激振力传递至天平浮动框表面后的力幅频特性曲线,并根据式(8)计算获得激励力输入a点与天平浮动框间的传力特性,如图13所示。
图14为某飞行器模型在进行脉冲风洞测力试验过程中风洞测试段总压和天平轴向输出信号图,虚线表示风洞试验段总压变化规律,实线表示天平轴向输出电压信号。从图中可以看出,总压上升阶段为风洞启动过程,总压稳定阶段为有效试验阶段,持续约500 ms。因此,在进行传力特性分析时可以将作用于飞行器模型表面的气动力等效成作用于模型a,b,c处分别沿x,y,z方向的阶跃力,如图15所示。基于傅里叶变换将阶跃力展开成谐波力信号,将模型a点-天平浮动框力传递特性曲线(如图13所示)中各频率的幅值和与之相对应的谐波力幅值相乘,就可以得到作用在a点处的各谐波力信号传递至天平后的幅值,再以天平测试分辨率为评判依据筛选出输入力中未被天平所感应到的谐波力成分,即找出幅值低于2 N的谐波力,分析结果表明,输入力中未被感受到的谐波力共有99个,其频率值离散分布在51~3 000 Hz,由式(10)计算出力在测力系统轴向方向上的传递误差ε为1.681 9×10-5,当a点激励力的幅值不断改变时,测力系统轴向方向上的传递误差ε如表10所示。由此表明,大部分的气动力在测力系统轴向上可以很好的传递。

图13 激励力输入a点与天平浮动框间的传力特性Fig.13The force characteristics between point a and balance float box

图14 脉冲风洞测力试验总压图Fig.14 The total pressure diagram of pulse wind tunnel force test
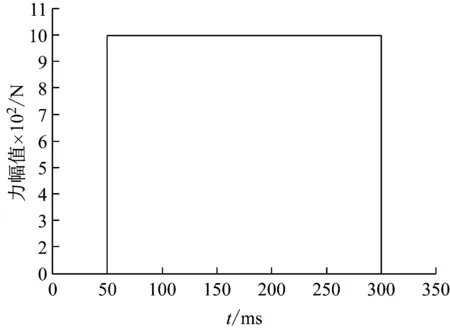
图15 作用于a,b,c三点的气动力Fig.15 Air force acting on a, b, c three points
4.4 测力系统纵向传力特性
采用如上方法,对测力系统纵向进行传力特性分析,b点处作用激振力时,得到单位激振力传递至天平浮动框表面后的力幅频特性曲线如图16所示,分析结果表明,输入力中未被感受到的谐波力共有304个,其频率值离散分布在51~3 000 Hz,由式(10)计算出力在测力系统轴向方向上的传递误差ε为5.920 1×10-5,当b点激励力的幅值不断改变时,测力系统纵向方向上的传递误差ε如表10所示。由此表明,气动力在测力系统纵向的传递损失较小,大部分的气动力在测力系统轴向上可以很好的传递。
4.5 测力系统径向传力特性
同理,对测力系统径向的传力特性进行分析,得到单位激振力作用在c点时激振与天平浮动框间的力传递幅频特性曲线如图17所示,分析结果表明,输入力中未被感受到的谐波力共有105个,其频率值离散分布在51~3 000 Hz,由式(10)计算出力在测力系统轴向方向上的传递误差ε为6.253 5×10-5,当c点激励力的幅值不断改变时,测力系统径向力的传递误差ε如表10所示。说明气动力在测力系统纵向的传递损失很小,大部分的气动力在测力系统轴向上可以很好的传递。

图16 激励力输入b点与天平浮动框间的传力特性Fig.16 The force characteristics between point b and balance float box

图17 激励力输入c点与天平浮动框间的传力特性Fig.17 The force characteristics between point c and balance float box

表10 测力系统传力特性 Tab.10 The force characteristics of force measurement system
5 结 论
本文围绕风洞测力系统传力特性评估开展研究,建立了测力系统整机有限元模型;得到了飞行器模型重心与天平间的传递特性可以描述整机传力特性的结论;获得了力在飞行器模型重心与天平浮动框间传递的幅频特性曲线;揭示了测力系统轴向、纵向与径向传力特性;通过对仿真结果分析,得出以下结论:
(1) 对测力系统进行了整机模态试验,提取了系统前4阶模态并与有限元仿真值进行了对比,其中第四阶计算模态与试验模态的误差达到10.3%,其余均在10%以内,由此验证了该模型的可靠性,从而保证了基于有限元模型的传力特性分析的可信度;
(2) 研究发现,基于傅里叶变化将作用飞行器模型重心处的阶跃力展开成一系列谐波力,并根据力在飞行器模型重心-天平浮动框间的传递特性计算各谐波力传递至天平浮动框后的大小,以天平的最小测试分辨率筛选出未被天平识别到的谐波力成分,计算未被辨识信号能量占原始信号总能量的百分比,以此来评估测力系统传力特性优劣的方法是可行的;
(3) 测力系统传力特性分析表明,1 000 N大小的气动力沿轴向、纵向与径向传递时,未被天平识别的谐波力信号能量占输入信号总能量的百分比分别为1.681 9×10-5,5.920 1×10-5,6.235 3×10-5,并且随着轴向力幅值的不断变大,传递误差均减小,气动力幅值由1 000 N逐渐增大至6 000 N时,轴向、纵向与径向的传递误差变化范围分别为:1.681 9×10-5~0,5.920 1×10-5~0,6.235 3×10-5~2.747 8×10-5,其中轴向传力误差最小,由此表明气动力在测力系统的轴向、纵向与径向能够很好的传递,测力系统具有良好的测试精度。
