不同台风下高层建筑气动阻尼比综合对比分析
2018-11-21张传雄李正农史文海潘月月王澈泉王艳茹
张传雄, 李正农, 史文海, 潘月月, 王澈泉, 王艳茹
(1. 温州大学 瓯江学院建工学院,浙江 温州 325035; 2. 湖南大学 土木工程学院,长沙 410082; 3. 温州大学 建筑工程学院,浙江 温州 325035)
由于城市化的加速,科学技术的进步,土地的高效利用,沿海城市的建筑正变得更加高柔,其结构特点为风敏感,小阻尼。而国内开始于上世纪末对于结构气动阻尼的研究业已取得相当的成绩。
Gabbai等[1]对高层建筑顺风向的气动阻尼进行了研究,得出其产生有利的影响结果,并且认为数值较小,经常可以忽略。Fu等[2]对加速度均方根与平均风速和阻尼比与加速度幅值的关系进行了研究,得出它们之间为幂级数关系的经验公式。吴海洋等[3]设计了一种质量和结构阻尼比可调的底部弹性支撑刚性体的双向摆式气弹模型,并通过气弹模型风洞试验提出了横风向气动阻尼比的经验公式。曹会兰等[4]通过37个超高层建筑气动弹性模型的风洞试验,利用随机减量法从模型的风致加速度响应中识别了气动阻尼,研究了独立矩形截面超高层建筑顺风向气动阻尼的变化规律。吴海洋等[5]将小波分析应用到结构风工程领域,介绍了一种基于小波分析的高层建筑既适用于单自由度高层建筑气弹模型又适用于多自由度高层建筑气弹模型的气动阻尼评估方法。嵇学培等[6]在边界层风洞中对432 m高的广州珠江新城西塔进行多自由度气动弹性模型试验。黄鹏等[7]通过风洞实验得出在某些特定情况下,高层建筑的气动阻尼比会出现负值,这将增加结构的动力响应。吴玖荣等[8]通过对风致加速度的分析,研究了其频谱特征、结构自振频率和振型等相关动力特征,采用随机减量法求得结构第一振型阻尼比与振幅的非线性关系。李小康等[9]针对439 m的深圳京基金融中心(KFT)工程,采用气动弹性模型技术研究其横风向气动阻尼特性。黄铭枫等[10]根据在北冕台风及汶川远震作用下某270 m高大楼顶层实测得到的加速度响应数据,对该高楼的结构动力参数和气动阻尼进行了识别。Cheng等[11]对气弹模型下气动阻尼比与折减风速的关系进行研究并得出经验公式。
上述文章对气动阻尼进行了较为深刻的分析,得到了诸多研究成果。但既有的研究大都是在风洞及气弹模型条件下,原型实测的结果较少。由于比例效应、风场模拟和模型形式的限制,风洞实验结果并非可以完全准确地模拟出结构的风致响应,因而原型实测正成为另外一个主要的获取高层建筑风效应的重要手段。
1 原型实测及理论方法
1.1 台风简介与实测过程
本文以温州市区某方形高层建筑为实验背景在不同台风下进行气动阻尼比实测研究,实验楼地上41层,高168 m,在台风期间,在实验楼顶部架设2台05103V型风速仪,并选择有代表性的41,32,25,18,10等楼层,在核心筒楼梯间处X,Y方向分别布设991型加速度传感器及扭转测试仪,均通过电缆与安装在25层设备层的优泰动态信号采集仪及专用电脑连接,以记录各台风影响前后的风场数据和结构运动数据,记录时间从七级风圈影响实验楼开始至台风登陆或过境后风速减小至5 m/s为止。实验楼及设备见图1和图2。


图1 实验楼Fig.1 The lab building


图2 风速仪、加速度传感器Fig.2 The nemometer and accelerometer
在2012~2016的五年间,选取对浙江温州市区影响较大的台风,分别为:“潭美”、“灿鸿”、“杜鹃”、“凤凰”及“尼伯特”,其线路除“凤凰”由南向北外,其它台风都是由东往西移动,见图3。
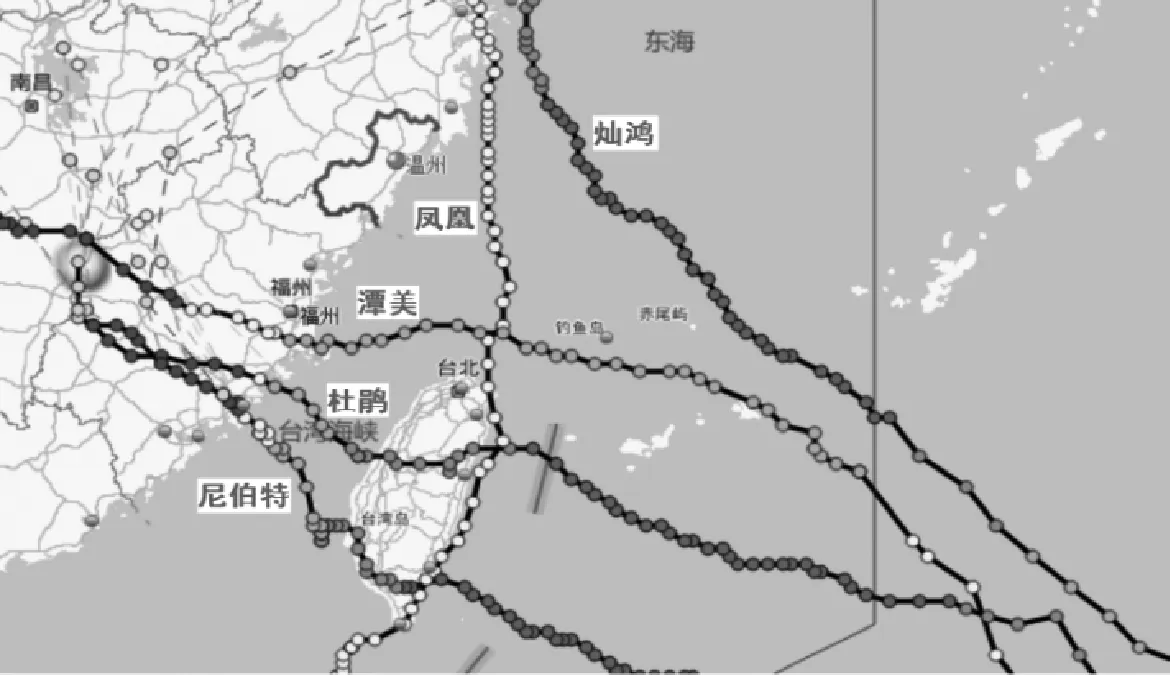
图3 台风线路图Fig.3 The typhoon route
选取各个台风有代表性的风速、风向角、结构速度、加速度时程的数据样本,时长约为260 min,进行计算分析。图4和图5为台风‘潭美’的10 min平均风速、风向角及结构响应的加速度、速度样本,由图可以看出,结构响应与风速及风向角有关,且与风速具正相关。
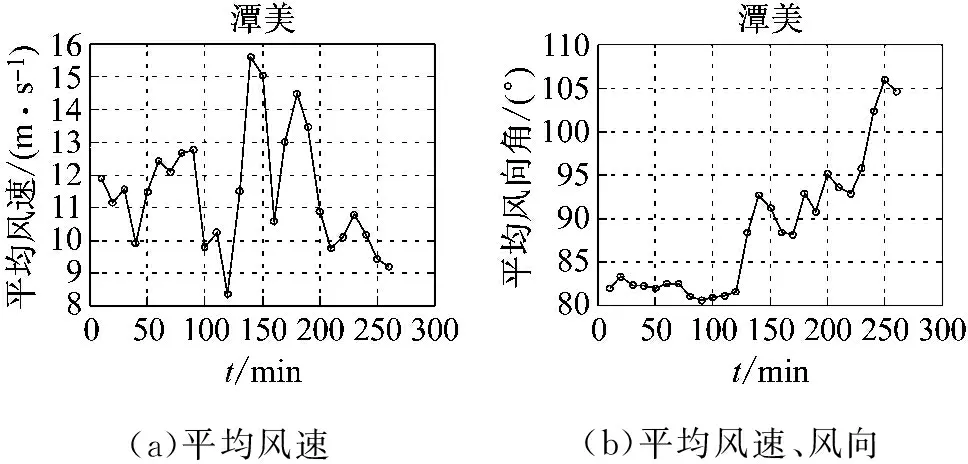
图4 台风“潭美”平均风速、风向(10 min)Fig.4 Mean wind speed,wind direction(10 min)

图5 台风“潭美”下结构加速度、速度极值Fig.5 Structural acceleration,velocity amplitude
1.2 理论方法
近年来,直接利用环境激励下的振动响应数据进行模态参数识别在各个研究领域中得到高度而且有效的应用。其方法无需费钱费力地对桥梁、海洋结构、高层建筑等大型结构进行主动激励,仅需直接测取结构在风力、交通、地脉动等环境激励下的响应数据再运用时域识别方法即可辨识出结构的模态参数。图6即为利用ERA-NExT方法得到的在台风作用下实验楼结构响应的前五阶振型。
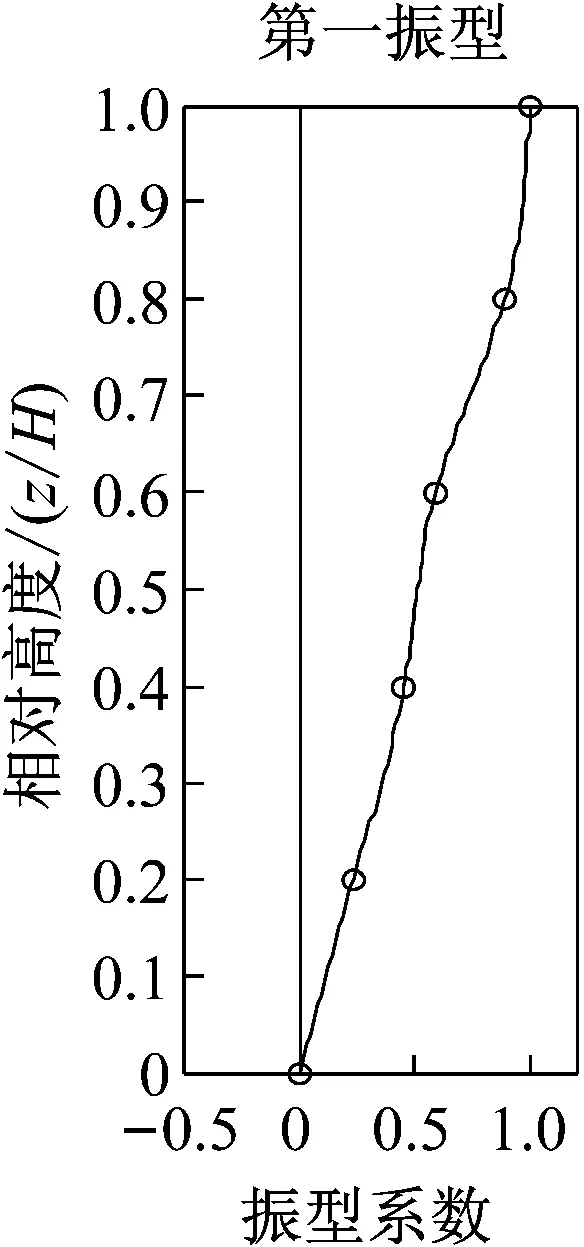
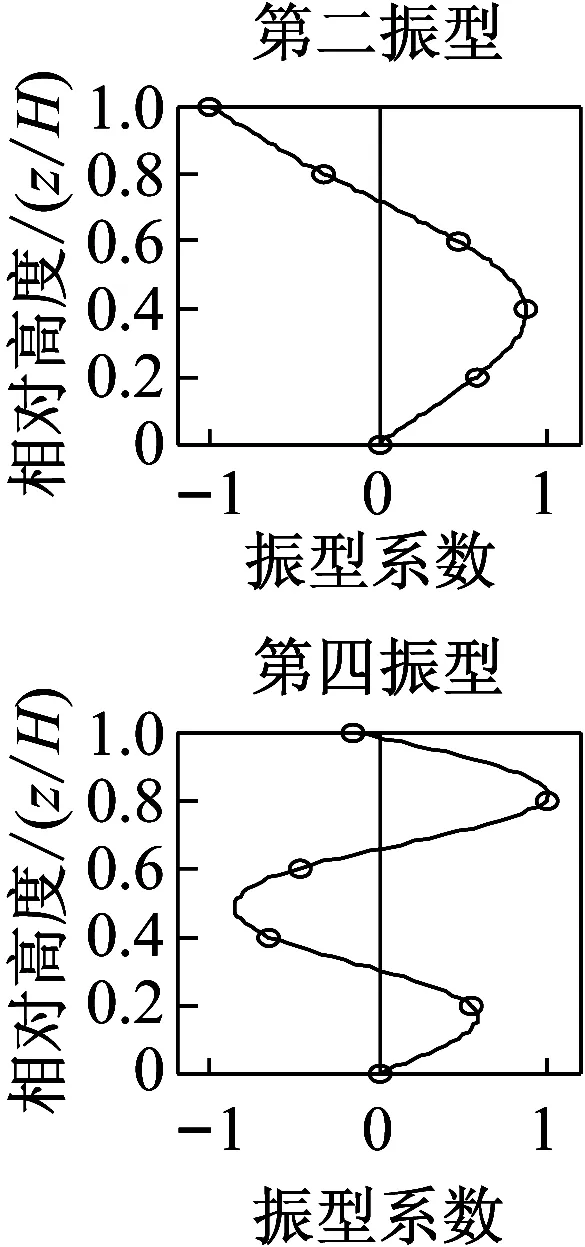
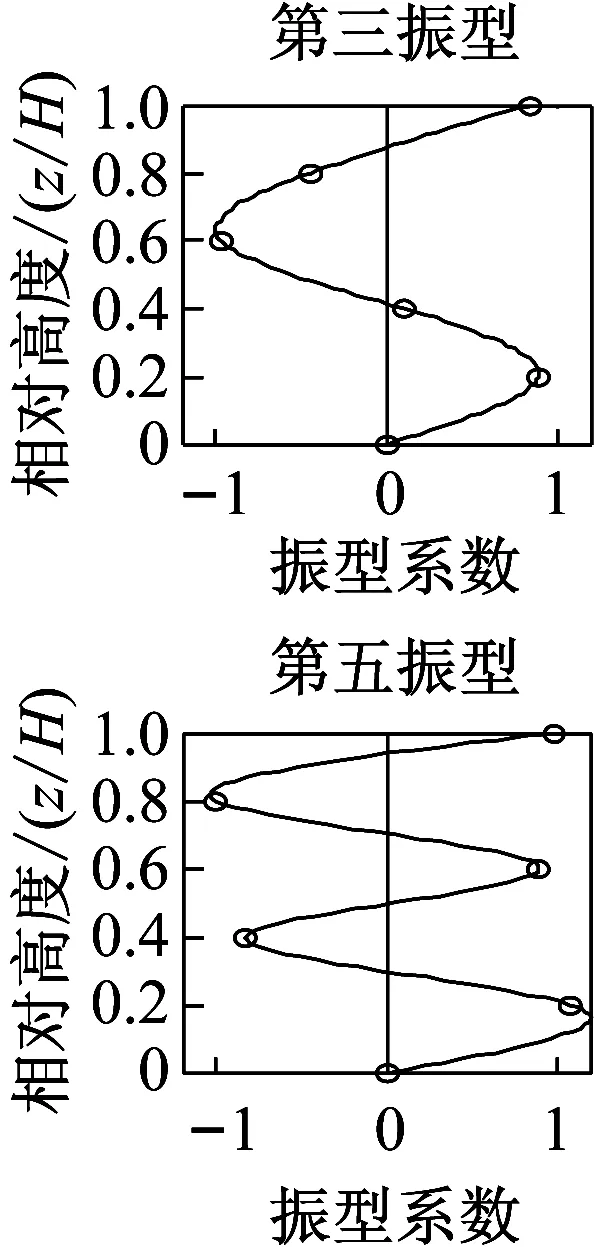
图6 台风“杜鹃”X向ERA-NExT法振型图Fig.6 Vibration mode of ERA-NExT method
应用上述方法,在数年里影响温州较为明显的几次台风环境下,在粗糙度流场、长宽比、宽高比等不变的条件下,本文以实验楼实测获得的屋顶风向、风速,及各楼层的加速度、速度数据为样本,经EMD预处理,应用NExT法将不同测点振动响应信号之间的互相关函数代替脉冲响应函数作为模态参数时域识别的输入数据。再运用基于模态参数时域识别的特征系统实现(Eigensystem Realization Algorithm, ERA)理论方法计算结构振型总阻尼比,风速趋于零时,总阻尼比值趋于稳定,此时获得的总阻尼比即为结构阻尼比。计算正常风速下结构振型总阻尼比,二者相减即得到气动阻尼比。对以上计算结果对应的风速、风向进行综合比对分析,总结得出在不同风向角下,气动阻尼比与来流风速及结构运动速度、加速度参数的关系规律,并根据黄铭枫等的结论应用三次多项式拟合了经验公式,以期能为同类建筑的结构抗风设计提供对比及参考依据。
2 风致振动分析
2.1 结构速度的均方根与平均风速
气流运动导致了结构的运动,因而结构速度的均方根与平均风速之间应具有正相关性。应用幂函数拟合其经验曲线,由图7可以得出,各台风结构速度的均方根与平均风速的关系,实测点分布在拟合曲线附近较为密集且具有明显的规律性,特别是台风“灿鸿”、“杜鹃”、“凤凰”,尤为明显。即随着平均风速的增加,结构速度的均方根也呈幂级数函数的规律增加,X,Y方向规律性基本相同。
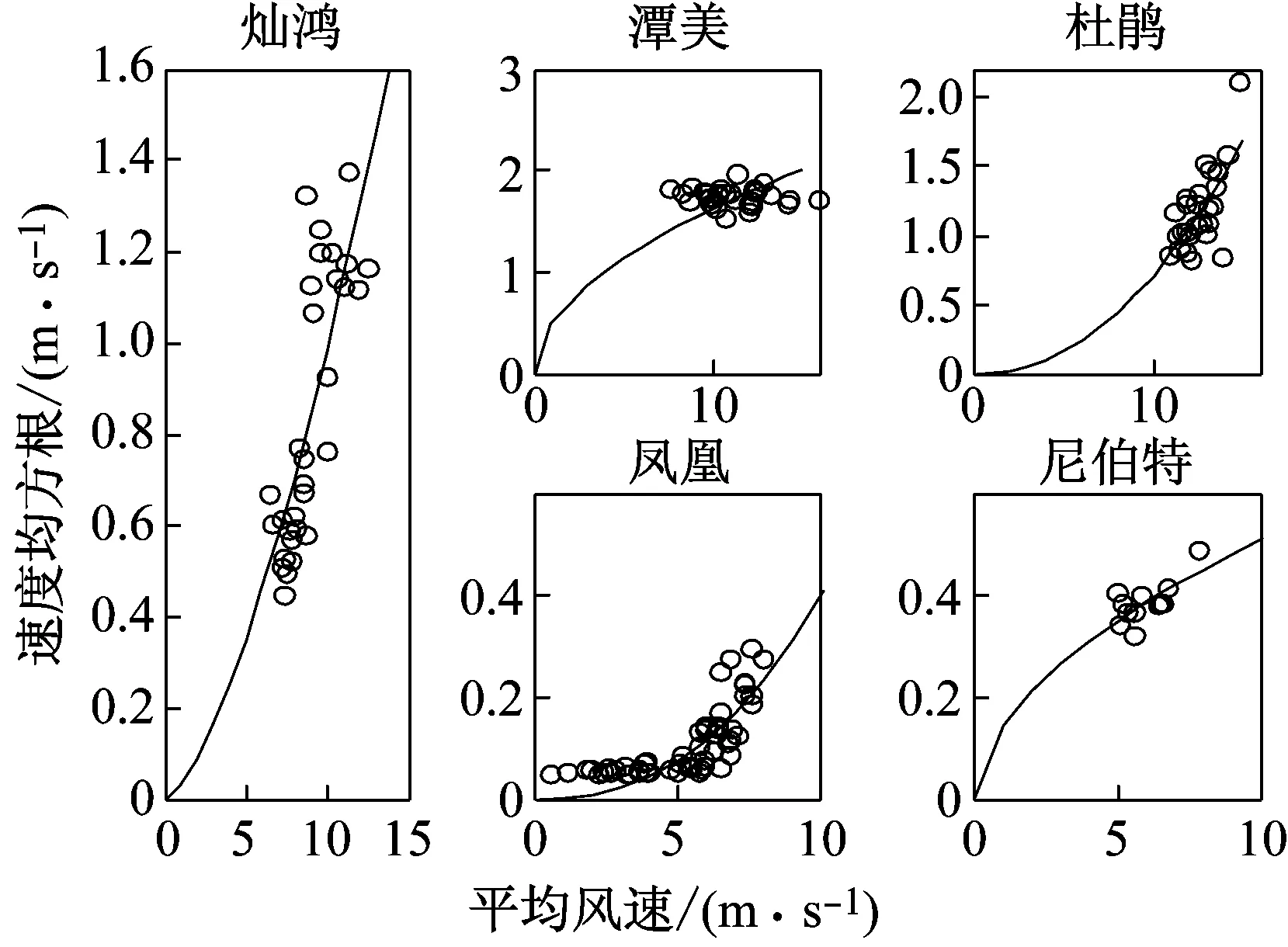
(a)X方向
(b)Y方向图7 各台风下结构速度的均方根与平均风速关系Fig.7 Relationship between the structural velocity RMS and the average wind speed for X and Y direction
由图8可以得出,X方向结构速度均方根数值大小与台风风向和X方向坐标轴的夹角的余弦具正相关性。台风风向和X方向坐标轴的夹角从小到大排列:“潭美”(10°)、“尼伯特”(25°)、“灿鸿”(40°)、“杜鹃”(38°)、“凤凰”(55°),在平均风速0~15 m/s内,各台风下结构响应速度均方根从大到小数值排列:“潭美”、“尼伯特”、“杜鹃”、“灿鸿”、“凤凰”,只是“杜鹃”、“灿鸿”顺序略有颠倒,原因可能是它们的风向角很接近,实测值有时便难以清楚区别。同样,Y方向结构速度均方根数值大小与台风风向和Y方向坐标轴的夹角的余弦具正相关性。台风风向和Y方向坐标轴的夹角从小到大排列:“凤凰”(35°)、“杜鹃”(50°)、“灿鸿”(52°)、“尼伯特”(65°)、“潭美”(80°),在平均风速0~7 m/s内,各台风下结构响应速度均方根并没有特别的规律,但在平均风速7~15 m/s内,各台风下结构响应速度均方根从大到小数值排列:“潭美”、“尼伯特”、“杜鹃”、“灿鸿”、“凤凰”,与夹角的升序排列完全相同。由此可以发现来流风速在结构运动方向的投影决定此方向的结构运动。
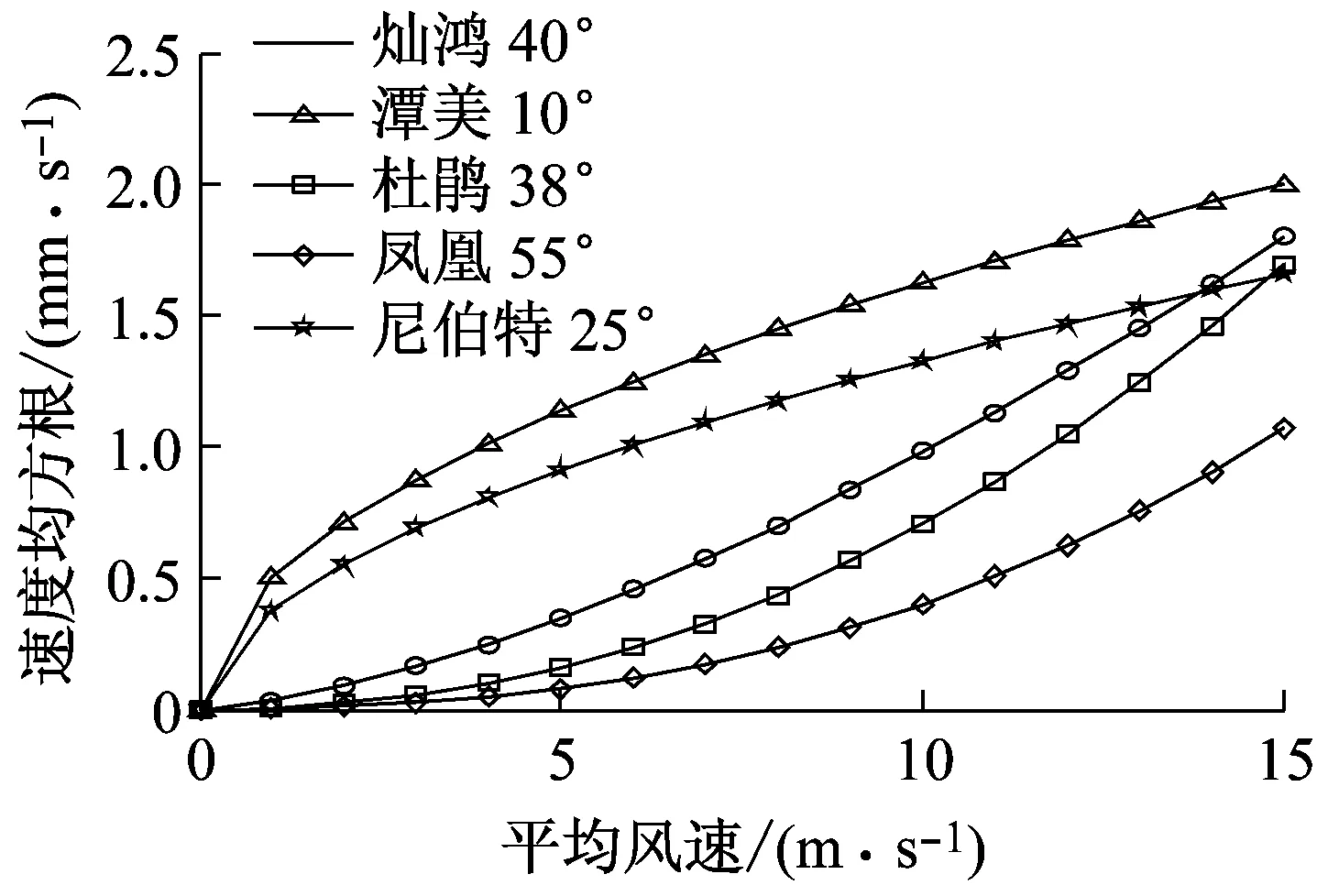
(a)X方向实测对比
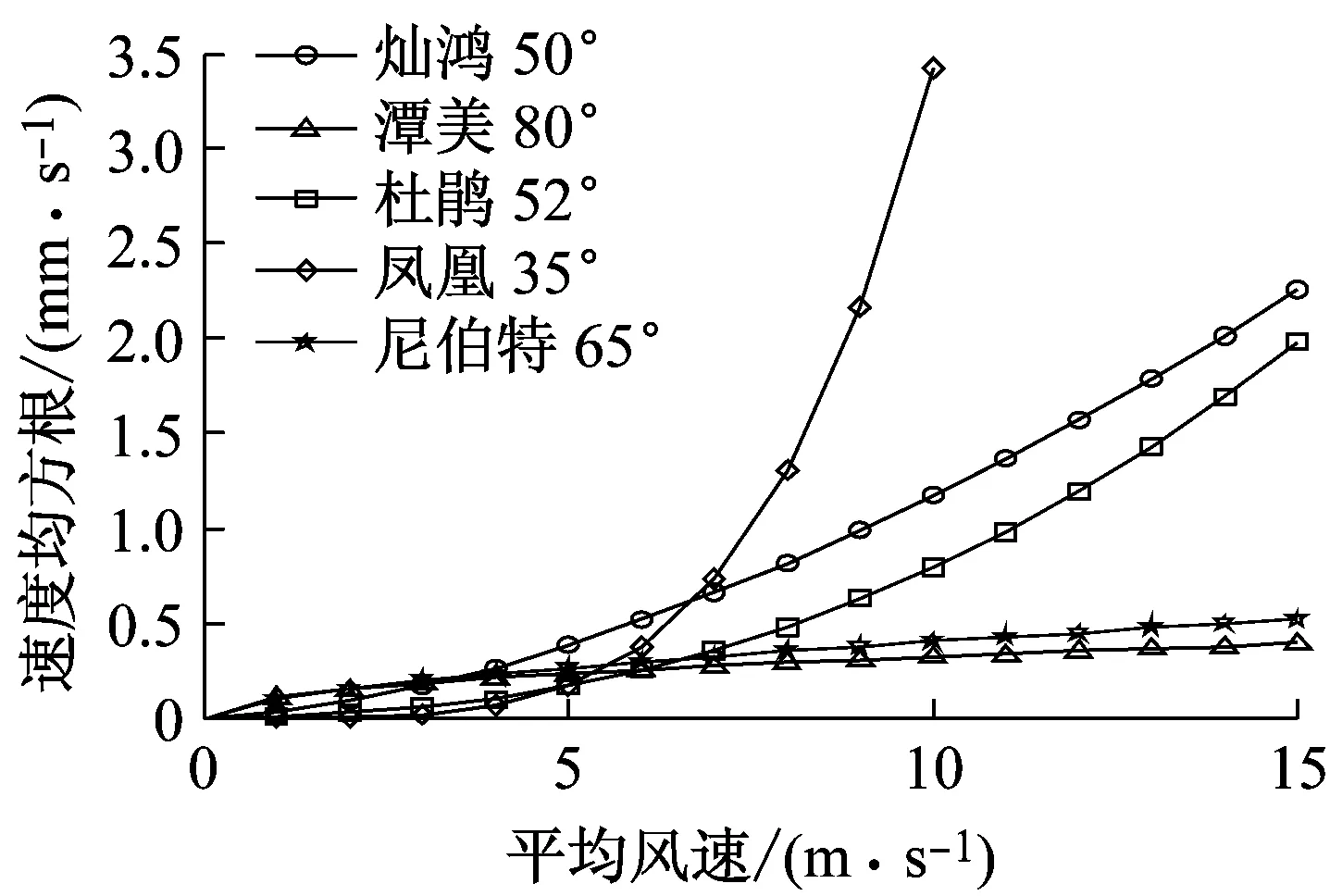
(b)Y方向实测对比图8 各台风下结构速度的均方根与平均风速的关系对比Fig.8 Contrast relationship between the structural velocity RMS and the average wind speed under different typhoons for X and Y direction
2.2 结构加速度的均方根与平均风速
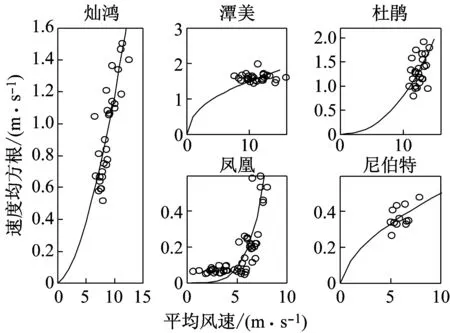
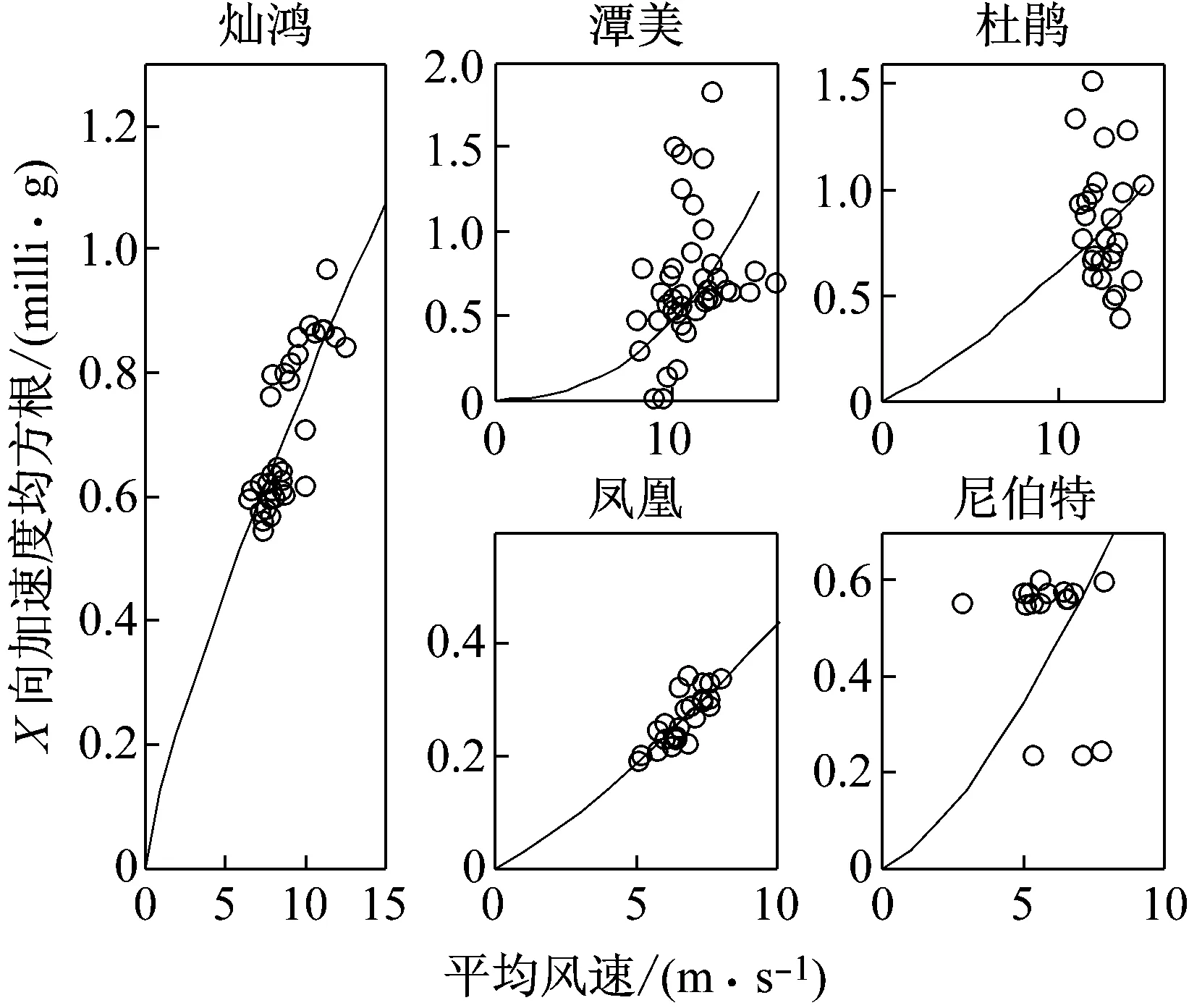
结构加速度的均方根与平均风速之间关系见图9、图10,与“3.1”节中结构速度的均方根与平均风速之间关系具有相似性,这可能与它们都是结构的运动特性有关。
3 气动阻尼比
3.1 气动阻尼比特性分析
影响建筑气动阻尼比的因素很多,如环境流场粗糙度、结构长宽比、高宽比、结构阻尼比、质量分布、折减风速和结构速度、加速度等,因为气动阻尼比是结构与来流的耦合作用,因而折减风速和结构速度、加速度是影响其变化的最重要的因素。而丹麦的克莱斯迪尔比耶和斯文奥勒汉森[12]在《结构风荷载作用》中也指出气动阻尼要注意的主要问题是强烈漩涡带来的振动危险,它取决于风速与临界风速的比值、雷诺数、周围的湍流强度和尺度等因素。特别由于风速功率谱是风场能量在频域上的度量,结构加速度功率谱是风场能量向建筑结构转移的能量在频域上的度量,其幅值也是影响气动阻尼比的关键因素之一,因而不能忽视。
本文根据数据样本,对影响气动阻尼比较大的因素如折减风速、结构加速度(速度)均方根与幅值比、加速度功率谱幅值进行了综合对比分析,以寻求其变化规律。
(a)X方向

(b)Y方向图9 各台风下结构加速度的均方根与平均风速关系Fig.9 Relationship between the structural acceleration RMS and the average wind speed for X and Y direction
3.2 研究方法的比较
(1)模态参数的识别方法
一般试验模态参数频域识别方法和时域识别方法的算法均属于单输入单输出多模态参数识别的范畴。这些算法主要是针对单个响应测点的实测数据进行模态参数识别。对于多个测点的模态参数识别,一般是通过逐点依次处理的方式来进行的,每次用一个测点的实测数据识别该测点的固有频率和阻尼比以及振型系数等模态参数。从理论上讲,从任一点实测数据所识别的固有频率和阻尼比都应相同,因为它们都属于总体模态参数,对于每个模态是唯一的。但由于测量和识别所带来的误差,从各测点识别得到的模态频率和阻尼比并不完全相同,特别是阻尼比经常差别较大。另外,当测点位置不理想时,上述算法的识别精度往往会受到较大影响。为了使固有频率和阻尼比达到一致,通常采用的方法是取识别结果的平均值来作为总模态固有频率和阻尼比。
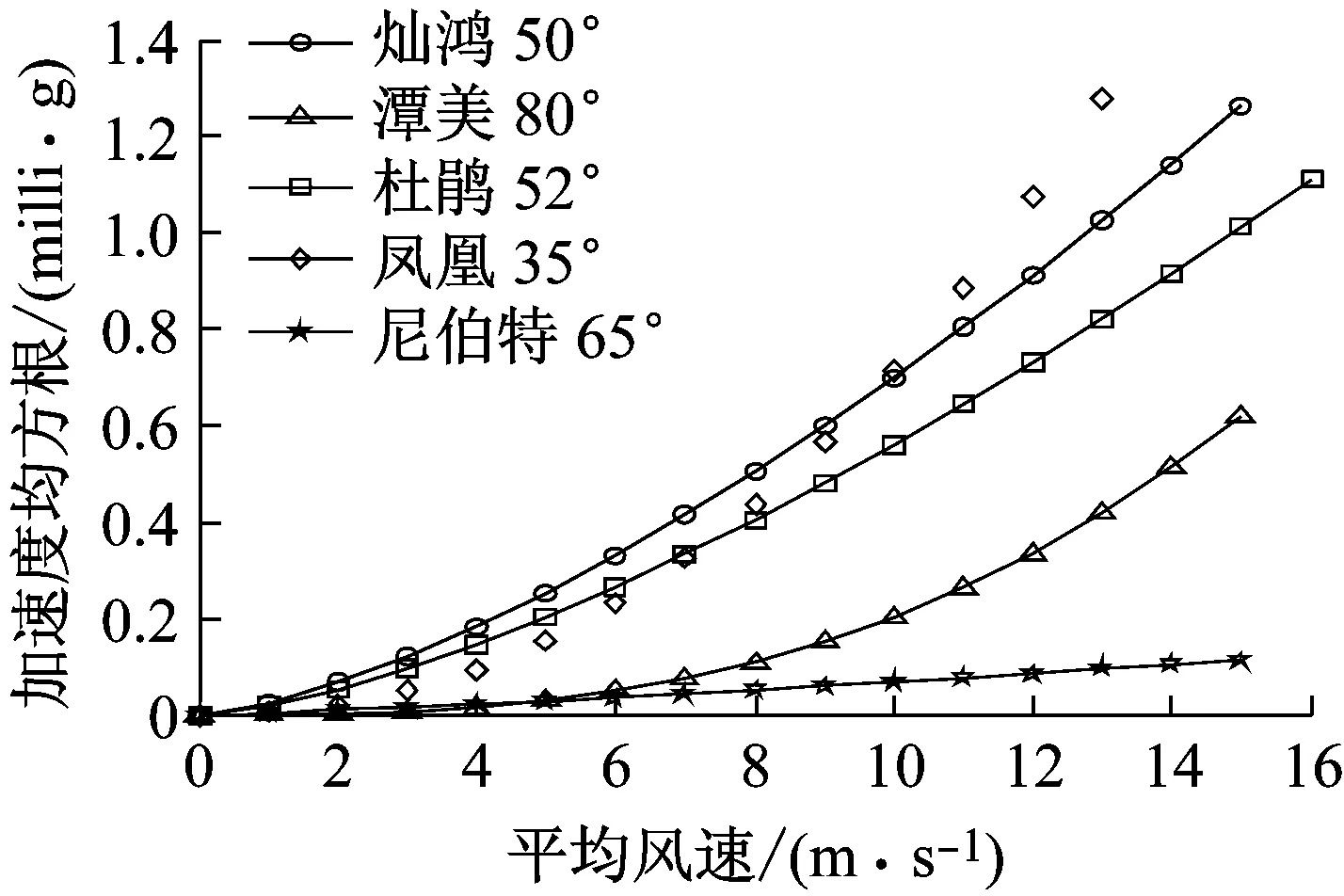
(b)Y方向实测对比图10 各台风下结构加速度的均方根与平均风速的关系对比Fig.10 Contrast relationship between the structural acceleration RMS and the average wind speed under different typhoons for X and Y direction
用单输入单输出法识别多自由度结构模态参数,至少要按测点数目重复多次,不仅计算量大,而且不同测点的识别结果一致性差,因而20世纪70年代末80年代初发展了同时采用全部测试数据的单输入多输出的整体识别法。模态参数的整体识别方法是将结构上所有测点的实测数据集中在一起进行统一的参数识别方法,所识别得到的结果为结构整体的模态参数,每阶模态的固有频率和阻尼比是唯一的。该方法的求解步骤一般是先利用所有测点的实测数据,识别出整体的固有频率和阻尼比,再根据所得到的这些整体模态参数利用各测点的实测数据分别计算其有关振型的参数。整体识别方法的优点是能充分利用所有测点的数据,减小随机误差,提高了算法的适应性和识别精度。
(2)两种计算方法的比较
利用上述的两种设计思想,选取其应用较为广泛且有代表性的两种方法:RDT-STD方法、NEXT-ERA方法作具体的比较。具体选用台风“灿鸿”顶层单层振动加速度数据,首先经EMD预处理,再应用揉合了RDT的ITD方法由振动自由衰减曲线得到建筑结构的阻尼比为单输入、单输出方法,图11为其振动自由衰减曲线。
具体选用台风“灿鸿”五个楼层振动数据,以底层为基础楼层,首先经EMD处理,再应用揉合了NExT的ERA方法得到建筑结构的振型阻尼比,为单输入、多输出方法,图12为其前五阶振型图。上述两种方法均利用环境激励得到的建筑结构响应数据作为分析的样本数据,得到总阻尼比。
本文应用数理统计中假设检验理论中的配对样本的t-检验方法判别此两种方法的优劣,其为单正态总体参数(均值)检验问题,计算值t=1.81,小于查表得到的t=2.04,表示两种方法得到的结果并无显著差异,即结论是两种方法均可以作为计算阻尼比的方法,如图13所示。但由两种方法得到的阻尼比计算值与统一拟合直线取值计算得到的标准方差,第一种方法为0.676 1,第二种方法为0.450 1,我们采用标准差来描述两种算法阻尼比识别结果与其数学期望的偏差程度,标准差越小说明算法用于阻尼比识别越稳定,由此判明后者的精确度较高,略优于方法一,而且方法二对数据的应用比较充分,结果更加合理,因此本文后面的实测值均采用方法二处理计算。
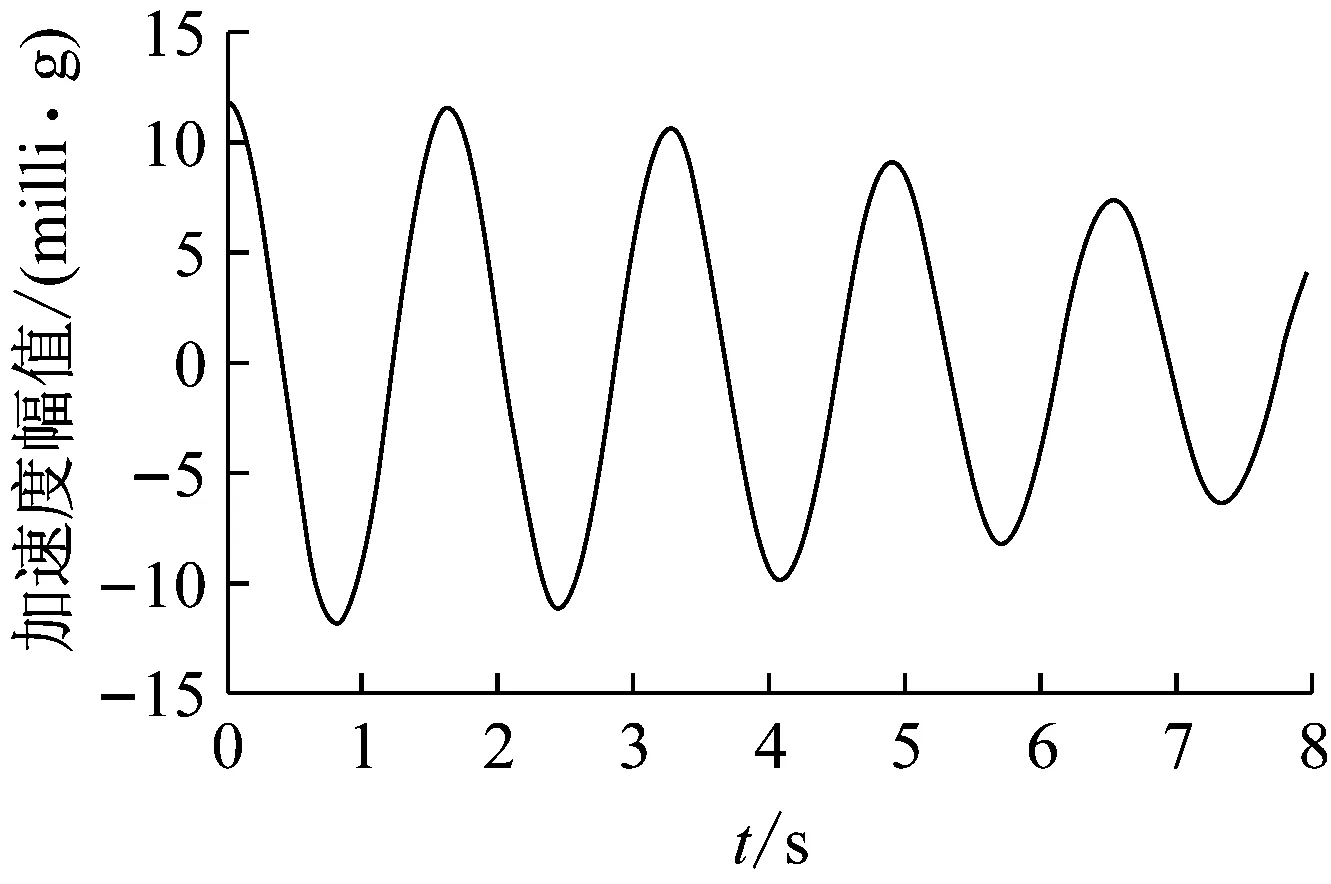
图11 自由振动衰减曲线Fig.11 Free vibration decay curve
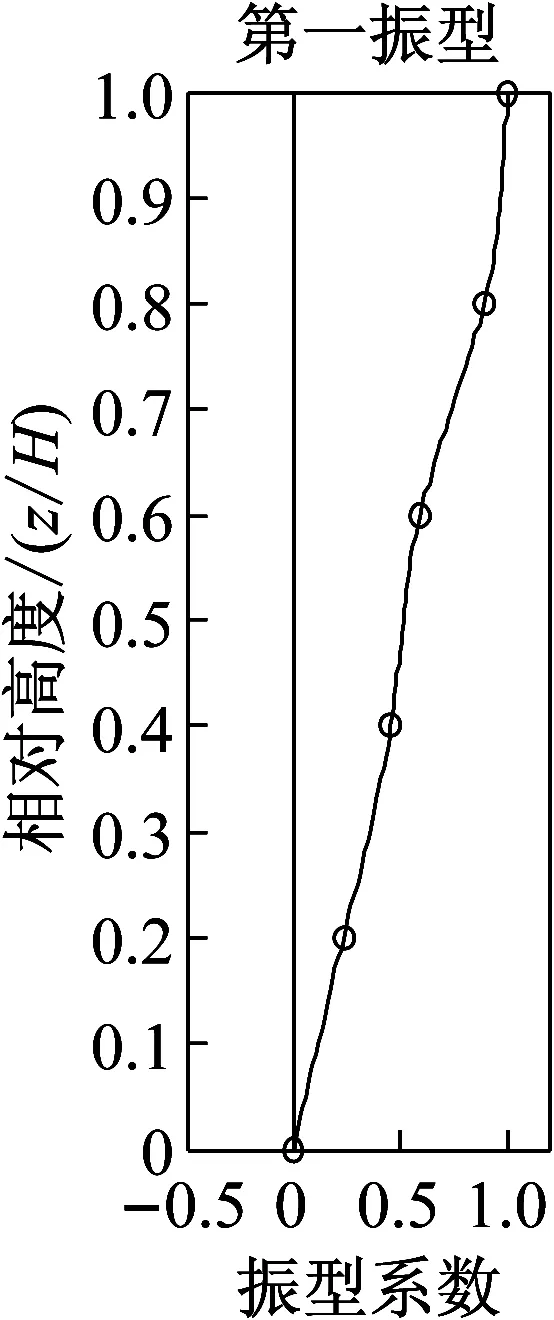
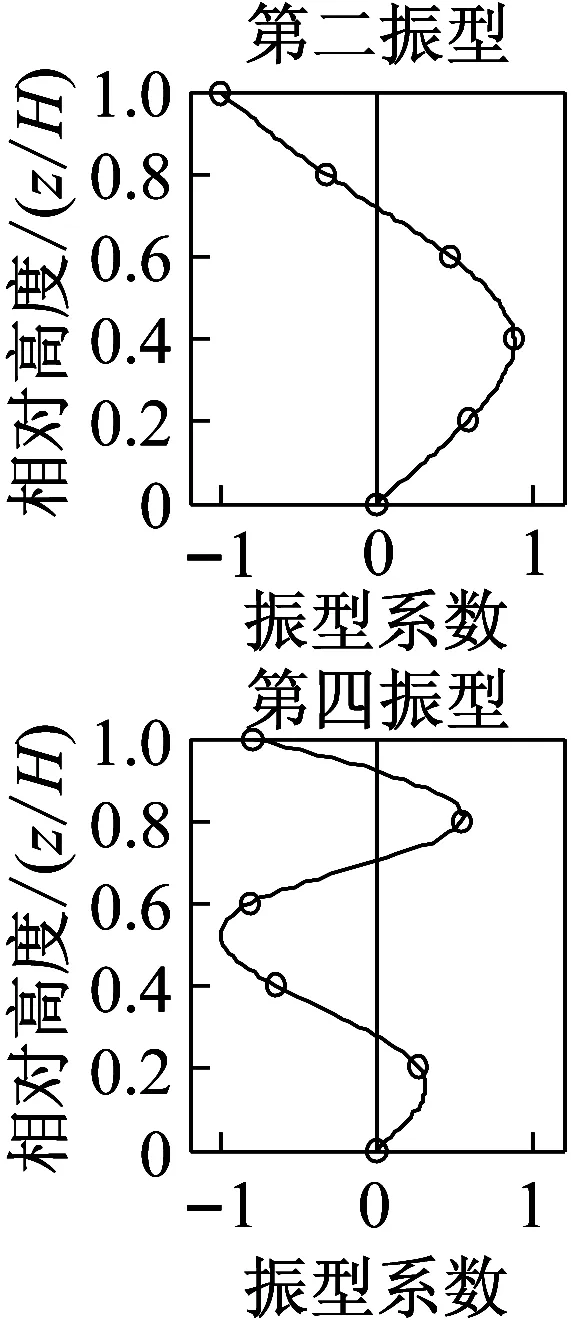
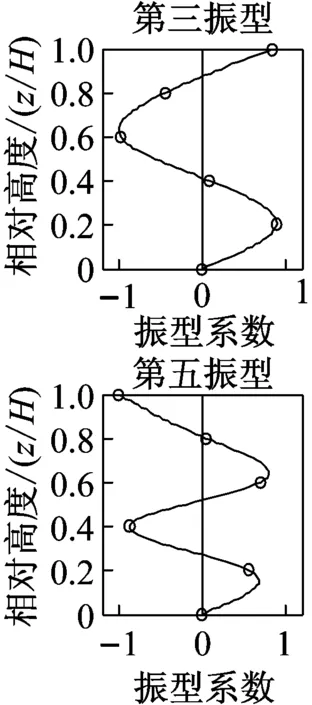
图12 前五阶振型图Fig.12 Front five modes of vibration
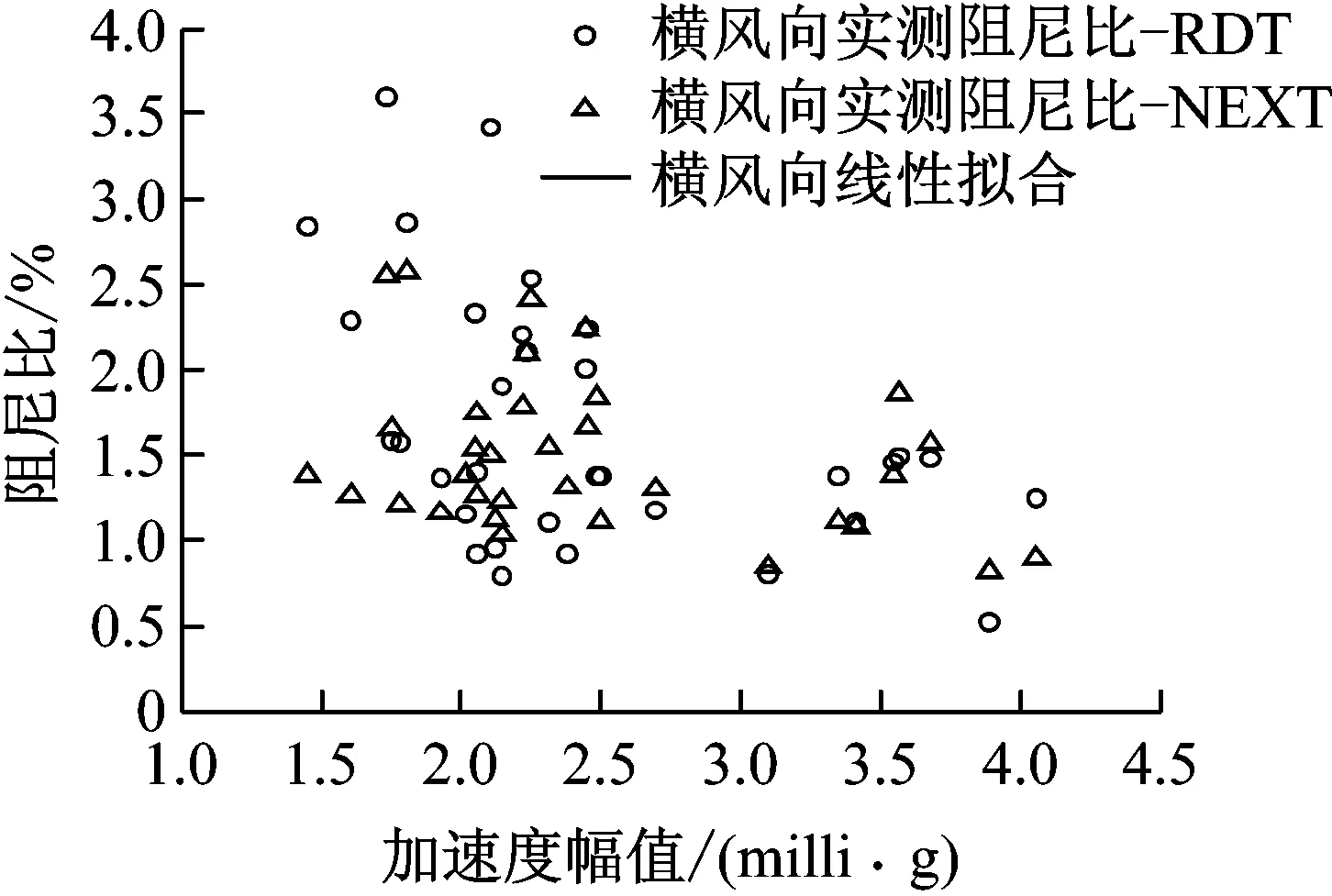
图13 两种方法的t-检验方法比较Fig.13 Comparison between the two ways of the t-check method
3.3 气动阻尼比与折减风速
折减风速是影响结构振型气动阻尼比的最重要的因素,以前的研究较为注重大折减风速(大于4)下的气动阻尼比的变化规律,对于小折减风速却较少涉及。在小折减风速范围内(小于1.0),气动阻尼比与折减风速的关系也不是纯粹单调的,而是分区间的。由图14可以得出,在较小折减风速的范围内,四个台风的变化规律均较为相似。X主轴方向的气动阻尼比,在折减风速小于0.5区段都是呈较大的递减趋势,在0.5~0.7到达谷底;然后分别在0.5~1.0呈平缓的递增趋势,至0.9~1.0到达峰顶,大于1.0段又是呈递减趋势。同样,Y主轴方向的气动阻尼比,在折减风速小于0.5段呈现增减不同,在0.5~1.0呈平缓的递减趋势,至0.9~1.0到达谷底,大于1.0段又是呈递增趋势。各台风在Y主轴方向的变化曲线的一致性远较X主轴方向复杂。
而且不同的台风在具体折减风速峰谷点位置各自稍有不同,这个不相同可能是由于他们不同的风向角导致的。
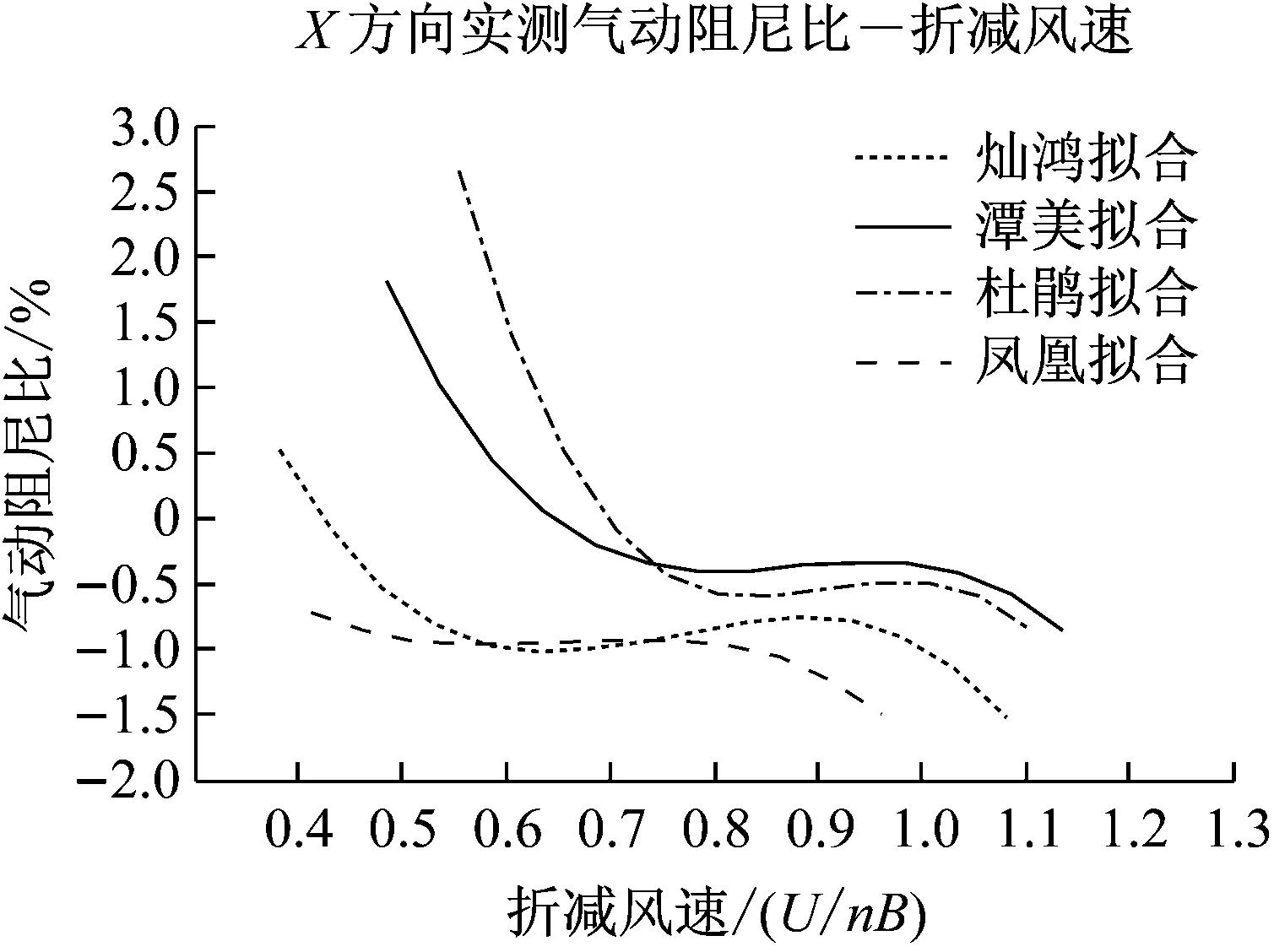
(a)X方向
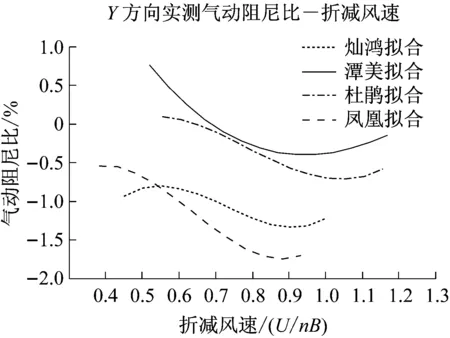
(b)Y方向图14 不同台风下X,Y方向气动阻尼比与折减风速的关系Fig.14 Relationship between the aerodynamic damping ratio and the reduced wind velocity under different typhoons for X and Y direction
3.4 气动阻尼比和结构加速度均方根与幅值比值
由图15可以得出,X向气动阻尼比随加速度均方根与幅值比值的增加而增加,而且其曲线数值大小的排列与风向角(与X轴的夹角)具相关性,拟合曲线在比值的0.15~0.20段变化陡峭,而在0.20~0.35段变化平缓,大于0.35又复归陡峭。Y向气动阻尼比随加速度均方根与幅值比值的增加而减小,而且其曲线数值大小的排列与风向角(与Y轴的夹角)具相关性,拟合曲线在比值的0.15~0.20段变化陡峭,而在0.20~0.30段变化平缓,大于0.30又复归陡峭。其中台风“凤凰”X向气动阻尼比的拟合曲线在整个区段的变化都较为平缓,而Y向气动阻尼比的拟合曲线在整个区段的变化都较为陡峭,这可能与其台风的强度、结构及路径有关,导致对实验楼的影响效应有别于其他台风。
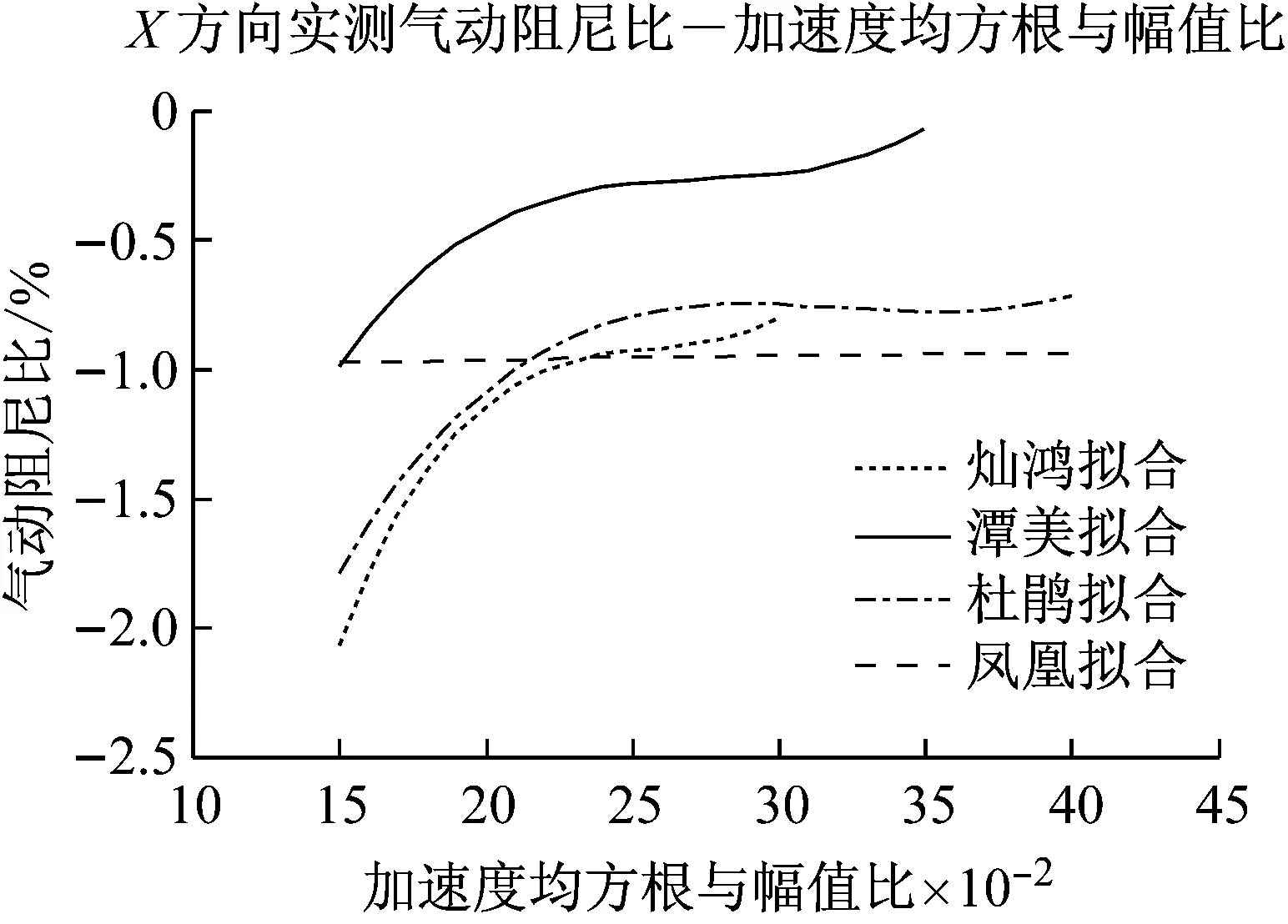
(a)X方向
(b)Y方向
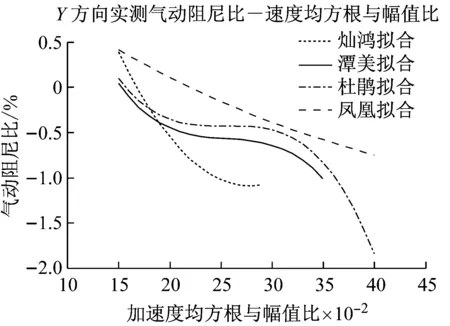
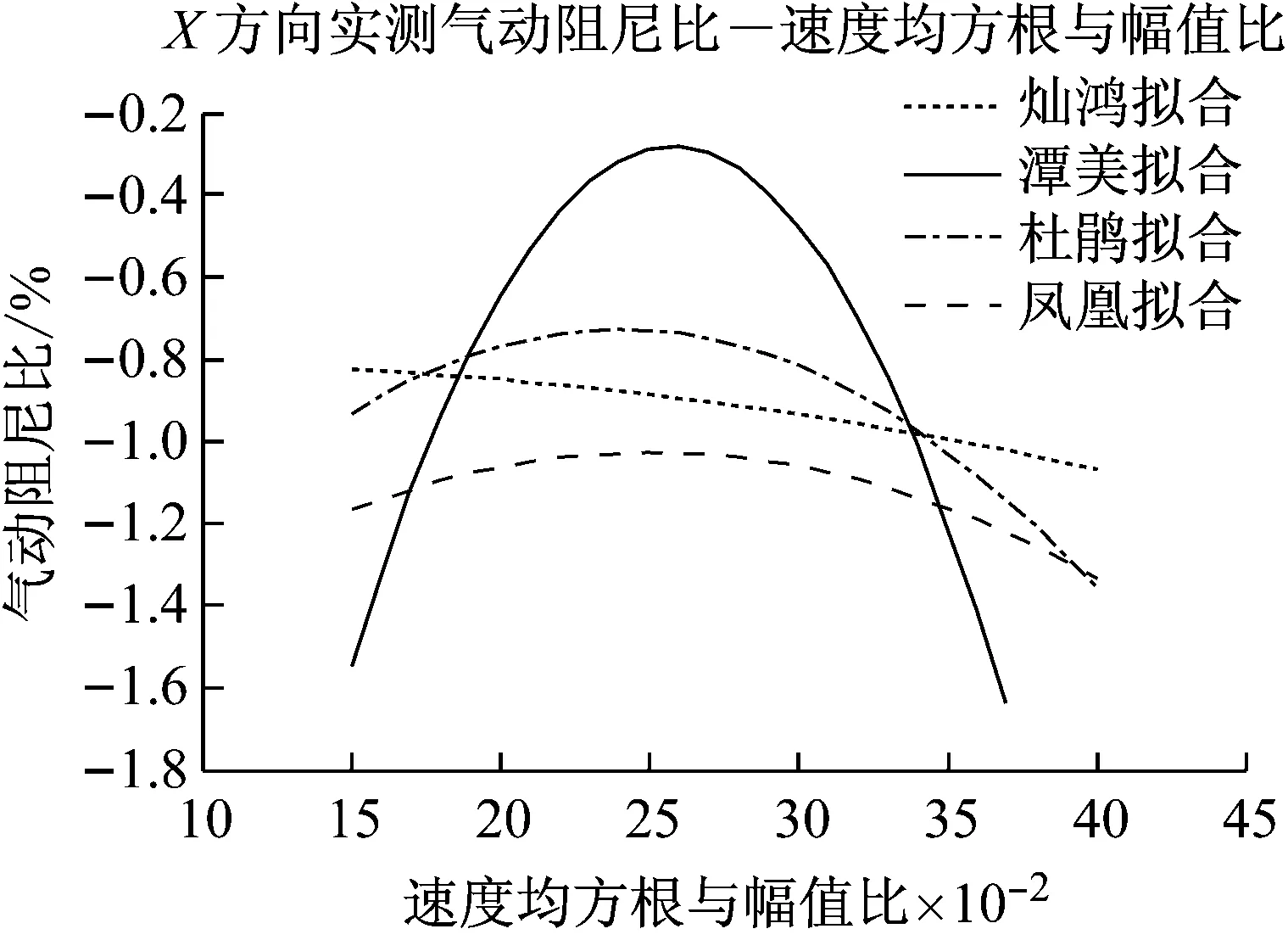
3.5 气动阻尼比和结构速度均方根与幅值比值
如果以二次多项式作为拟合的函数,在一定的区间[0.15,0.40]内,一次项是主要变化项,二次项是调整项。由图16可以得出,在区间[0.15,0.25]内,X向气动阻尼比随速度均方根与幅值比值的增加而增加,在区间[0.25,0.40]内,X向气动阻尼比随速度均方根与幅值比值的增加而减小,除‘灿鸿’外,其余均在0.25左右到达峰顶;而Y向气动阻尼比却正好相反,在区间[0.15,0.25]内,Y向气动阻尼比随速度均方根与幅值比值的增加而减小,在区间[0.25,0.40]内,X向气动阻尼比随速度均方根与幅值比值的增加而增加,除“杜鹃”在0.30外,其余亦在0.25左右到达峰顶。而且它们曲线排列顺序与其风向角具相关性。
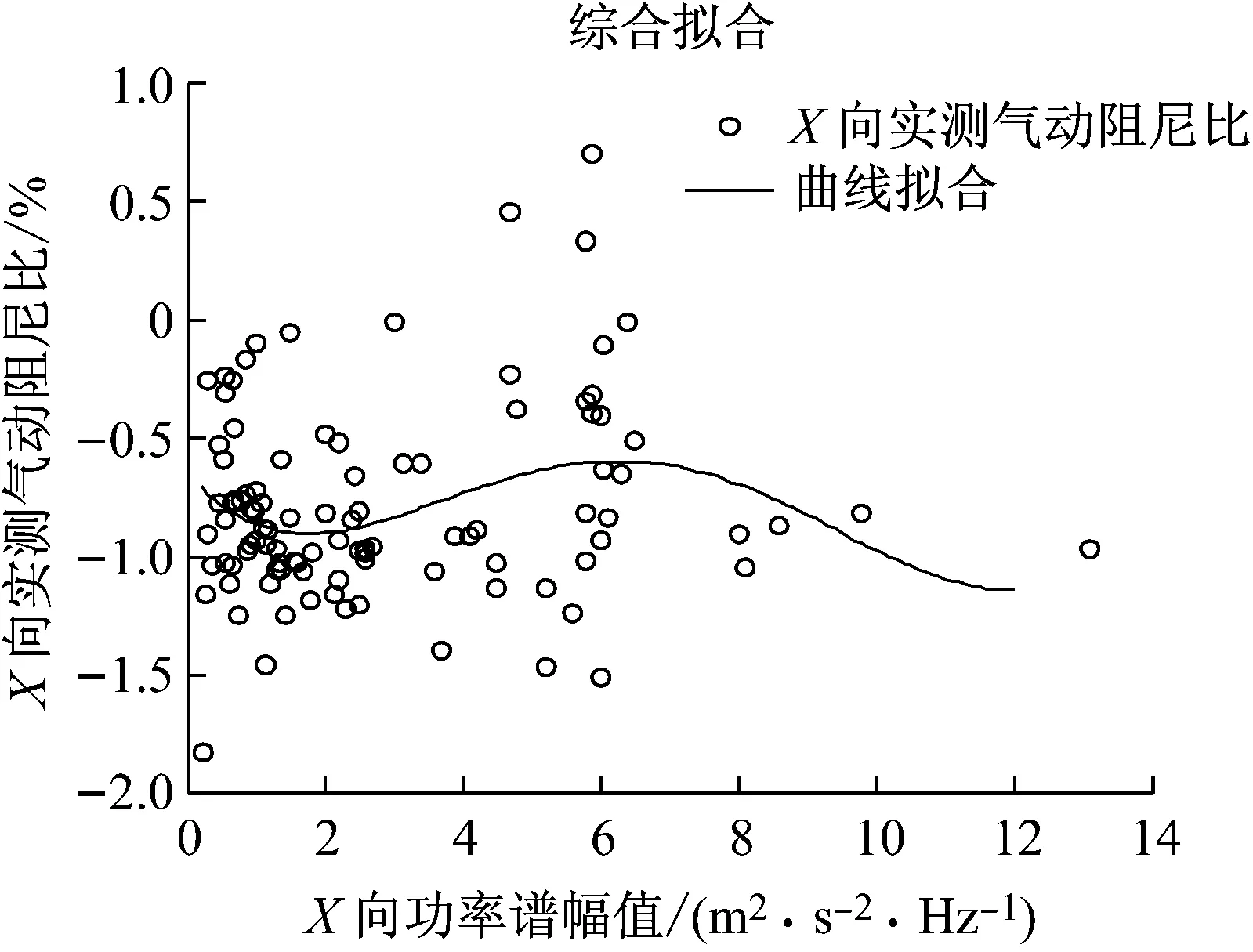
3.6 气动阻尼比与结构加速度功率谱幅值
由于结构加速度功率谱幅值是结构运动在频率分布能量大小的度量。通过对多次多项式拟合结果的比对,用四次多项式拟合各台风条件下气动阻尼比与结构加速度功率谱幅值的关系规律富有特点,结果如图17所示。由图17可以得到,结构加速度功率谱幅值在[0,2.0]区段,气动阻尼比随结构加速度功率谱幅值增加而减小,2.0左右为其谷底;在[2.0,6.0]区段,气动阻尼比随结构加速度功率谱幅值增加而增加,6.0左右为其峰顶;[6.0,12.0]区段,气动阻尼比随结构加速度功率谱幅值增加而快速减少。X,Y方向具有非常相似的特性。
(a)X方向

(b)Y方向图16 不同台风下气动阻尼比和速度均方根与幅值比值的关系Fig.16 Relationship between the aerodynamic damping ratio and the ratio of velocity RMS and amplitude under different typhoons for X and Y direction
(a)X方向

(b)Y方向图17 气动阻尼比与结构加速度功率谱幅值的关系Fig.17 Relationship between the aerodynamic damping ratio and the amplitude of acceleration power spectrum for X and Y direction
4 结 论
本文基于单输入多输出的ERA-NExT方法进行多台风下气动阻尼比实测对比研究。结果表明:
(1) 随着平均风速的增加,速度、加速度均方根沿着幂函数增加。
(2) 在小折减风速范围内(小于1.0),气动阻尼比与折减风速、加速度(速度)均方根与幅值比值的关系也不是纯粹单调的,而是分区间增减变化,虽然四个台风的区间范围稍有不同,但变化规律却比较相似,而且其曲线数值大小的排列与风向角大小具相关性。
