基于EEMD-HHT的近岸冲流带波浪非线性波动特征分析
2018-11-21蒋昌波李志威刘晓建
邓 斌, 蒋昌波, 李志威, 刘晓建
(1.长沙理工大学 水利工程学院,长沙 410114;2.水沙科学与水灾害防治湖南省重点实验室,长沙 410114;3.长沙理工大学 水科学与环境工程国际研究中心,长沙 410114)
波浪向近海岸传播过程中,由于床面地形变化和建筑物的影响,会发生折射、绕射、反射、破碎、能量耗散等现象,其波要素和波能量在近岸带呈现强非平稳和非线性特性[1-2]。冲流带(Swash zone)作为海陆相互作用最直接的区域之一,是海岸带中水动力作用最活跃和泥沙运动最激烈地带[3-4],其水动力特性和体)泥沙运动对海陆相互作用的强度、海岸演化、海岸建筑稳定性以及海岸带生物的生长繁殖等发挥极其重要作用[5]。与破碎区波浪运动特性不同的是,该区域的波浪上爬和回落时间通常较短、水流加速快,加之水深较浅,实测非常困难[6]。目前针对该区域的水动力特性、泥沙输运过程和海滩冲淤变化的研究十分欠缺。其中,冲流带涉及到诸如波浪非线性相互作用等复杂的冲流振荡运动。因此,研究冲流带波浪水流在不同时间尺度上变化的周期性,对于深入认识波浪的演化及其对岸滩的作用具有重要科学意义。
在过去的几十年里,学者们通过各种方法开展研究,对冲流带内的水动力特性和泥沙运动规律已有较丰富的认识[7],普遍认为冲流带内一次典型的冲流主要包括上爬流(Uprush)和回落流(Backwash)2个过程[8-9]。由于破碎区内破碎波是高度非线性,波面上的水流净质量通量远大于波面以下,因此回落流与之产生的碰撞效应将对近波面附近产生更重要的影响,导致能量频谱特性发生变化。Guza等[10]最早在缓坡上采用电阻丝和压力计测量波浪的上爬运动,研究了冲流带的水动力特性,并发现冲流振荡所产生的非重力波频段与入射波高的增大呈线性增加趋势。冲流带是低频能量通常被反射到海上和短波(海浪或涌波)最后耗散发生的区域。在这个区域内,入射波与前一次的冲流之间的相互作用会导致低频波浪的进一步形成和反射[11]。前人对2种不同岸滩类型上冲流带水动力过程开展了研究,对于反射性岸滩,低频波被反射回去,高频波迅速在岸滩上发生破碎(卷破或崩破),导致高频波在冲流带内占主导地位;对于耗散性岸滩,相对较缓的岸滩坡度加强了低频波的发展,导致进一步的发生浅水效应并最终发生破碎[12-13]。由于低频波的耗散和高频波在较缓的岸滩上发生的激破,低频波的运动在耗散性岸滩占主导地位[14]。可见,岸坡的坡度不同,不同频率波浪其作用机制完全不同,有必要开展不同坡度下岸滩上波浪振荡非线性特性的研究。
众所周知,水波信号是一种非稳定、非线性的信号[15]。近年来,对于非线性信号的分析,主要包括快速Fourier变换(Fast Fourier Transformation,FFT)[16]、小波分析[17]和希尔伯特黄变换(Hilbert-Huang Transform,HHT)[18]。其中,传统的信号研究主要基于Fourier变换,但Fourier变换所要处理的信号必须是线性稳定的,对非线性不稳定的信号按照线性稳定处理,不能精确反映局部信号频率的瞬时性变化,无法将时间和频率联系在一起并达到很高的精度。小波分析虽然在处理非平稳非线性信号能力以及信号在时间域和频率域之间的相互转换上有了进一步提高,但它的本质是一种加窗Fourier变换,仍然不能使信号的时间域和频率域的相互关系达到很高的精度。在此基础上,Huang等[18]利用经验模态分解方法(Empirical Modality Decomposition Method,EMD),把信号分解成若干个窄带的过程,获得有限数目的固有模态函数(Intrinsic Mode Function,IMF),然后再利用Hilbert变换,得到时频平面上能量分布的Hilbert谱、边际谱和边际能量谱等,提出了希尔伯特黄变换,从而可以实现瞬时频率—能量的分析。
波浪破碎区和冲流带内的流动具有强非线性性、强波散性和强瞬变性,是研究冲流带泥沙输运机理的关键,传统的傅立叶分析和小波分析不能有效地描述其特性,吴耀祖等[19-20]指出HHT方法可用于水波运动分析,能有效探究整体现象内在的非线性、波散性和瞬变性,显示序列随时间变化的内在性质。很多学者采用HHT进行了海洋动力特征的分析,如Senthilkumar等[21]采用HHT方法分析了混合浪的群波运动特性,并指出了HHT方法可适应于非线性和非稳态过程的分析。Hwang等[22]分别采用HHT、FFT和小波分析3种方法对比分析了对海洋实测风浪数据进行非线性和非稳态分析,定量对比分析了不同频率下能量谱结果。李志强等[23]采用EMD方法对波浪信号进行分解,发现低频区能量对滩面泥沙起动起到主要作用,还有王扬圣等利用HHT对水体波动特征进行分析,发现波动具有一定的周期性,并且周期长短受外界影响。但由于EMD存在模态混叠和端点效应等问题,当前所做研究的观测值与真实值仍然有一定的差距[24]。
本文旨在运用EEMD-HHT得到试验波高信号的归一化能量谱、边际谱和边际能量谱,从而分析冲流带内水体波动非线性特征。为了更精确描述波浪对冲流带滩面的水动力作用,本文尝试采用消除端点效应的集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)[25-26]对波浪信号进行分解,运用HHT方法对不同坡度岸滩下试验测量的波浪加以分析,探讨该方法在破碎区、冲流带研究中的有效性,并对比分析不同坡度下近岸冲流带波浪的非线性特征。
1 研究方法
1.1 试验设备与布置
本试验在总结前人对冲流带水动力特性及岸滩演变的试验研究后,考虑试验水槽的尺寸,采用溃坝产生涌浪的特性对冲流带水动力特征进行试验研究,弥补现有可控环境下试验研究条件的不足。试验在长沙理工大学水沙科学与水灾害防治湖南省重点实验室的多功能水槽中进行,水槽尺寸为20 m×0.4 m×0.5 m,总体误差小于1 mm,水槽两侧为透明玻璃。本研究在水槽内设置溃坝生成涌浪试验装置,如图1所示,在水槽左端用两块厚2 mm的铝板封闭,其中右边铝板设置为可上下移动的闸门,与水槽两侧形成一个1 m长、0.4 m宽的水库。闸门顶部采用不可拉伸的细绳连接,通过滑轮,细绳另一端配重10 kg,闸门的开启通过电磁开关控制配重的释放。闸门可在0.2 s内被完全抽起,溃坝产生的波浪在下游发生卷破,并形成高强度的涌浪和随后的冲流事件。为弥补现有室内试验研究的不足,同时为能描述实际岸滩的复合坡形态,应考虑不同岸滩坡度对冲泻区流动特性的影响,本试验考虑陡坡(1∶10)、缓坡(1∶35)及复合坡(1∶35/1∶10)3个坡度的光滑定床分别概化冲流带岸滩地形,其中斜坡起点位于x=0 m位置,试验布置如图1所示。

图1 波浪水槽试验布置图Fig.1 Scheme of wave flume arrangement
试验闸内水位(上游水位)h1为0.28 m,下游水位h2为0.10 m,初始水深比h1/h2=2.8,溃坝涌浪属性概化如图2所示。根据Yeh等[27]的结论,试验中闸门离斜坡坡脚的距离设置为2 m,近似达到30η0(η0=hm-h2),从而确保涌浪得到充分发展。涌浪的传播速度U0及波头下部的水深hm可通过Froude数建立关系式
(1)
式中:hm可通过浅水波理论进行求解。

图2 溃坝涌浪属性Fig.2 Properties of a bore generated from a dam-break conditions
(2)
根据式(1)和式(2),计算得到U0=1.55 m/s,hm=0.17 m。涌浪的初始强度可通过离岸的Froude数表示:F0=U0/(gh2)1/2=1.56。当涌浪传播到岸线附近时,由于h2沿斜坡逐渐减少,因此涌浪的传播特性也随之改变。
由于冲流带内水深非常浅,采用接触式的电容式浪高仪难以测量到中、高冲流带的波高变化。为了获得整个冲流带内水位的时空变化特征,本试验采用电容式浪高仪(加拿大RBR公司生产的WG-50型)和非接触式的超声波水位计(德国GE公司生产)分别测量岸滩前和岸滩上的波高变化,其中,浪高仪的精度可达0.15%,超声波水位计测量精度达0.2 mm。试验坐标轴以坡脚中心线为中点,水流方向为x轴方向,垂直水槽边壁的方向为y轴方向,垂直底面的方向为z轴方向。为了验证浪高仪和超声波水位计测量的统一性及精度,将WG1浪高仪和UWG1号水位计布置于同一位置,所有浪高仪和水位计均布置于y=0的平面上,即水槽中间断面,具体布置见表1。试验前,浪高仪和超声波水位计均按标准进行严格标定。实验工况如表2所示。

表1 浪高仪及超声波水位计布置位置Tab.1 Locations of wave gauge (WG) and ultrasonic water level gauge (UWG) m

表2 试验工况Tab.2 Experimental conditions
1.2 数据分析方法
1.2.1 聚合经验模态分解
前人在运用EMD时,若信号的时间尺度存在跳跃性变化,IMF分量中会有个别分量包含不同的时间尺度[28],此类情况称为模态混叠。同时EMD分解过程中,所分析数据的结果会出现发散效应,导致结果的失真,即端点效应。针对EMD方法的不足[29],Wu等提出了一种噪声辅助数据分析方法聚合经验模态分解,由于白噪声的频率具有均匀分布的特点,所以将白噪声作为背景加入到信号中,不同尺度的信号区域将自动整合到与白噪声相关的适当尺度上,使信号在不同尺度上具有连续性,经过EMD分解得到IMF,再将IMF做整体平均运算用于消除白噪声的影响,最后得到的均值IMF就是EEMD分解后的结果。在EEMD分解过程中,加入的白噪声次数越多,经过均值后得到的信号越真实,分解后的IMF分量具有更加客观的信号信息,从而有效地抑制了模态混叠现象和端点效应的问题。
EEMD分解的具体步骤如下:
步骤1首先将白噪声n(t)加入到原始信号x(t)中,得到整体序列X(t),即
X(t)=x(t)+n(t)
(3)
步骤2对x(t)进行EMD分解,得到IMF分量c1j(t)和余项rn(t)。
步骤3重复N次步骤1和步骤2。
步骤4将上述得到的IMF分量cij(t)(其中i=1,2,3,…,N)进行整体平均运算,最终得到EEMD分解后的各个IMF分量cj(t),即
(4)
式中:N为重复添加白噪声运算的次数,取N=300;cj(t)为EEMD分解后所得的第j个IMF分量,其中每次添加白噪声的振幅为整体序列标准差的20%。经过EEMD分解后,有效的解决了EMD的模态混叠现象,本文亦选用EEMD算法对采集的波浪进行相应的分析。
1.2.2 希尔伯特变换
利用EEMD将信号分解为有限个IMF,为分析各IMF 频率特性,对式(4)中每个IMF作Hilbert变换,则各IMF做希尔伯特变换后,Re取实部,可以得到信号的瞬时频率为
(5)
式(5)右边称为Hilbert时频谱,简称Hilbert谱
(6)
Hilbert谱描述了信号幅值随频率和时间的变化规律。用Hilbert谱进一步定义Hilbert边际谱为
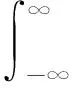
(7)
希尔伯特边际谱反映信号振动的特点,很好地表现信号的频率-幅值分布。Hilbert谱体现时间-频率-能量的三维状态信息,若不考虑频域的变化,只考虑某一个时刻的能量,则可得到原始信号的边际能量谱,更加直观地体现信号信息。
2 试验结果与分析
2.1 水体波动特性分析
波浪在近岸带形成大量紊动,存在多个上爬和回落的冲流周期,且水深较浅、流速较快,实测较难。为保证试验的准确性和稳定性,选择试验下3组工况的一个完整冲流周期,选取的波段分别为:case 1是7.6 s、case 2是8.6 s、case 3是17.5 s。进一步对比分析断面信息,对空间坐标进行无量纲化
(8)
式中:x为断面到坡脚点的水平距离;l为静水面高度;Rx为一次冲流过程的水平长度。
选出经过无量纲化后相同的断面信息(β=-0.25,β=-0.05,β=0.5,β=0.65),则每个工况下选择了4组断面,共12组数据进行EEMD分解。以case1 WG7为例,采样频率f=200 Hz,图3是试验波况分解后的IMF分量及其趋势分量,可见该波浪被分解成了不同波段波动过程,有助于分析不同波况下冲流带水体波动特征。在水位增加和降低处波浪信号波动明显,经过EEMD分解后各IMF分量在此时也受到了较大影响,但较好的表现波浪信号的幅值信息。
对各IMF分量运用FFT求得周期-功率谱曲线(见图4),周期运动在功率谱中对应尖锋,可知波况存在几个不同的周期历时,且从小到大依次排列,表明波浪信号包含了几个不同的时间尺度。对比原始信号与各个IMF分量,发现IMF6,IMF7与原始信号波形变化情况基本相同,且各个IMF分量所占比重各不相同,其中IMF6和IMF7的方差贡献率分别为20.02%和65.74%(见表3)。可见,IMF7为该工况下所波浪的主要成分,同时其平均振幅也较大,表明它的波动对时序变化的影响程度很强。因冲流过程时间较短,图4中IMF7能量主要出现在波动末期,难以判定IMF7分量的周期。但与此同时,试验条件下发现一次冲流过程不存在波浪对岸滩冲流带最大冲击历时的周期性变化,仅存在几个短期的周期性作用,对于case 1的WG7分别为0.07 s,0.18 s,0.38 s,0.84 s,1.52 s,2.53 s(见图4)。此外,趋势项res表示整个波动序列的变化趋势,在整个时间步长内先增加后减小,以5 s为分界点,波动振幅由增加变为减小,受波动序列时长的限制,其周期性并不明显。
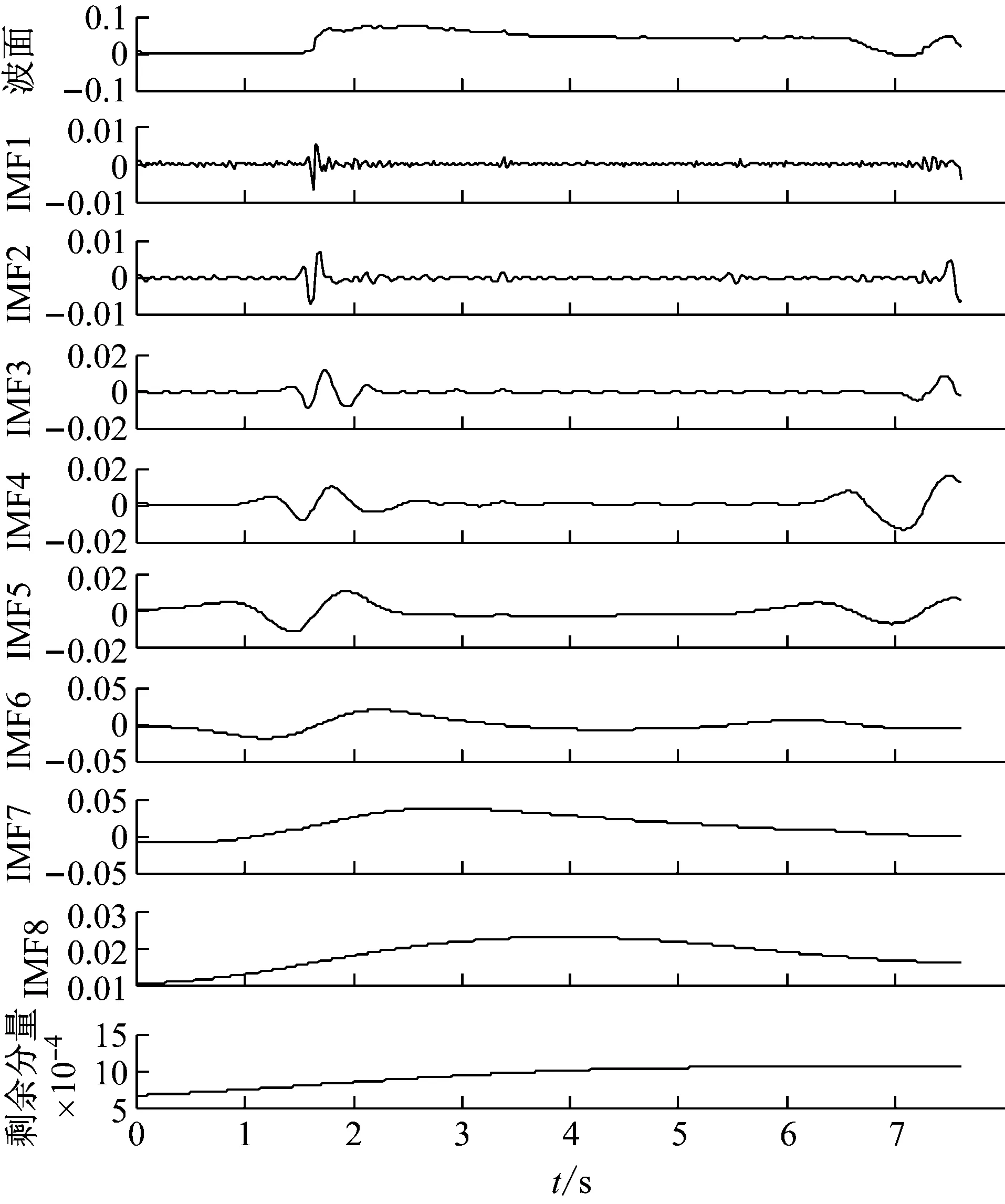
图3 波浪的IMF分量及其趋势分量(case 1 WG7)Fig.3 IMF component and its trend of wave measurements for WG7 of case 1
基于EEMD分解得到IMF序列,进行Hilbert变换,并经频率整理形成HHT的时频谱值图(见图5)。为了能清楚看到冲流带波浪传播变形随时频演化的过程,采用二维平面等值线图表示能量变换特征的时频演化过程。从图中可见能量的变化不是连续的,而是离散的,在没有能量的区域谱值一般为0,而有能量分布相对集中的区域可明显看出2个已知成分,主要表现为带状和齿状,谱值能很好地反映波能量随时间和频率的动态变化特征。带状和齿状图形集中程度和形成谱值空间图像正好反应了调频调幅成分和波浪信号成分的实际变化特征。从波浪的时频谱演化特征可以看出,冲流带波形信号的非线性动态变化特征可被HHT方法较好地描述出来。从演从化过程可知,记录到的波浪波动过程是非线性的、动态的;同时,EEMD-HHT方法可清楚的描述波浪形态动态细微变化过程,反应了冲流带波浪运动的阶段性,每个阶段都对应各自的频率特性、能量差异;此外,时频图上的能量主要集中在波高达到最大值之后才释放,与IMF序列曲线相对应。图6为计算得到的Hilbert边际谱和Hilbert谱,可知能量主要在低频段出现,约小于1 Hz,且能量变化受噪声的影响较小,所以在分析低频段能量变化时可不考虑噪声影响。在整个时域内,能量随着频率的增大出现的概率逐渐降低。
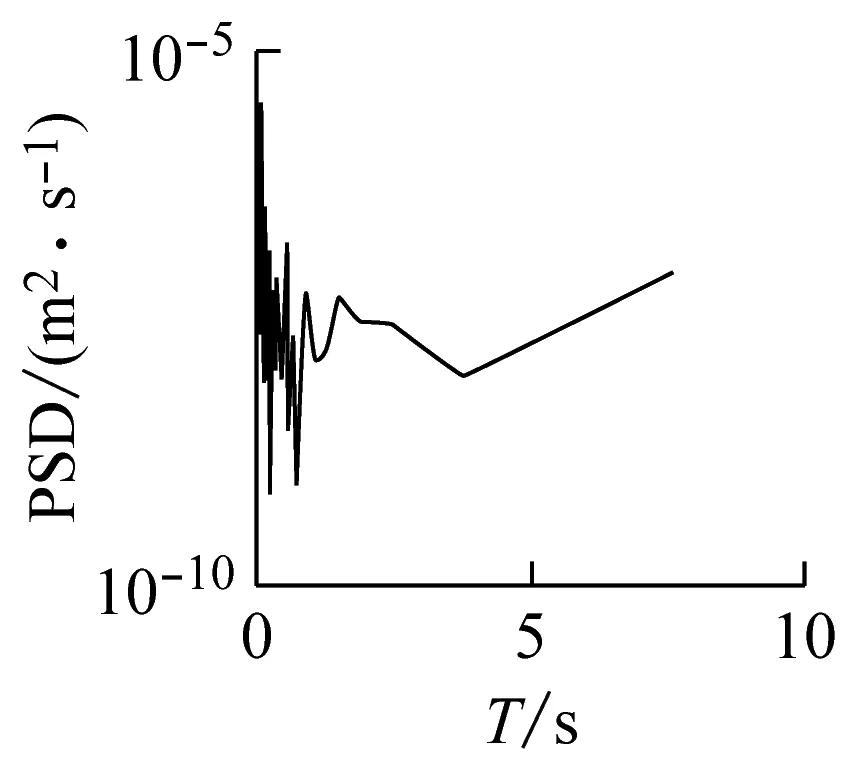
(a)IMF1
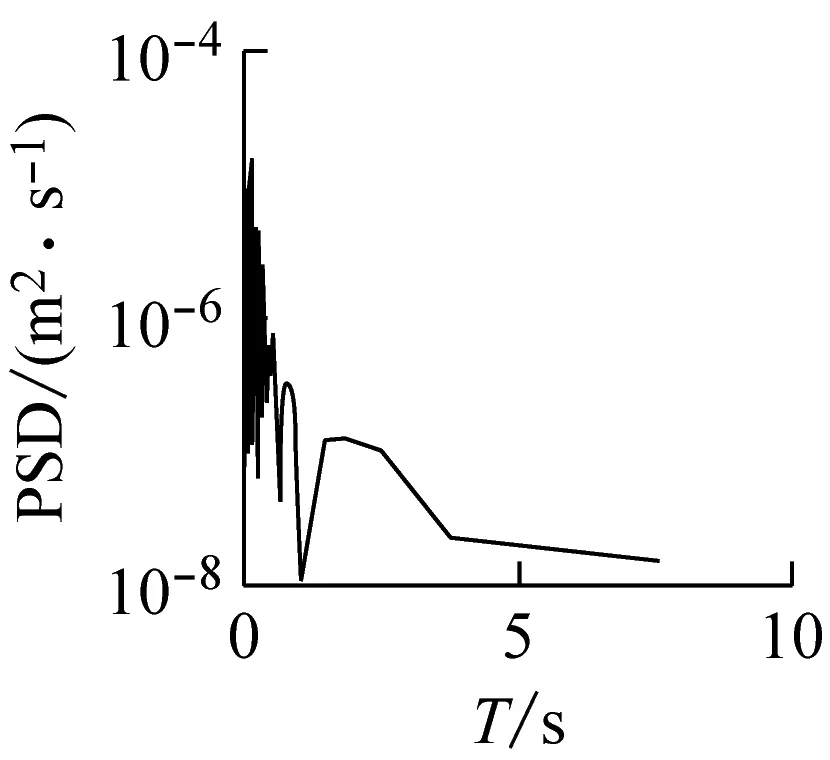
(b)IMF2

(c)IMF3

(d)IMF4

(f)IMF6

(g)IMF7
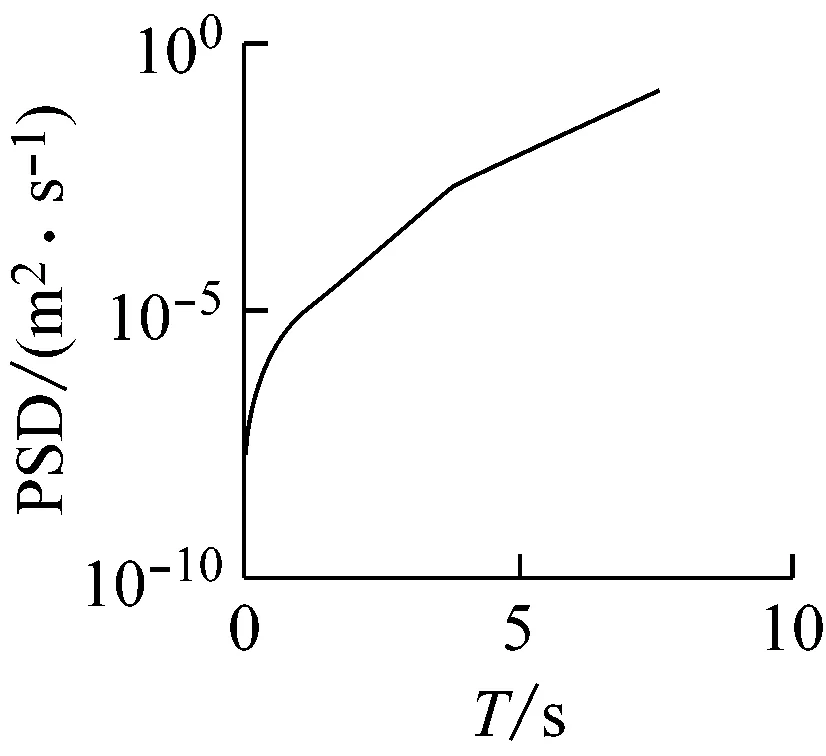
(h)IMF8图4 各IMF对应的周期-功率谱图(case 1 WG7)Fig.4 The Fourier power spectrum of IMF in case 1 WG7

表3 波浪的IMF分量的方差贡献率Tab.3 Variance contribution of wave IMF component

图5 HHT时频图(case 1 WG7)Fig.5 Spectrogram of HHT in case 1 WG7
2.2 波浪对岸滩作用的能量分析
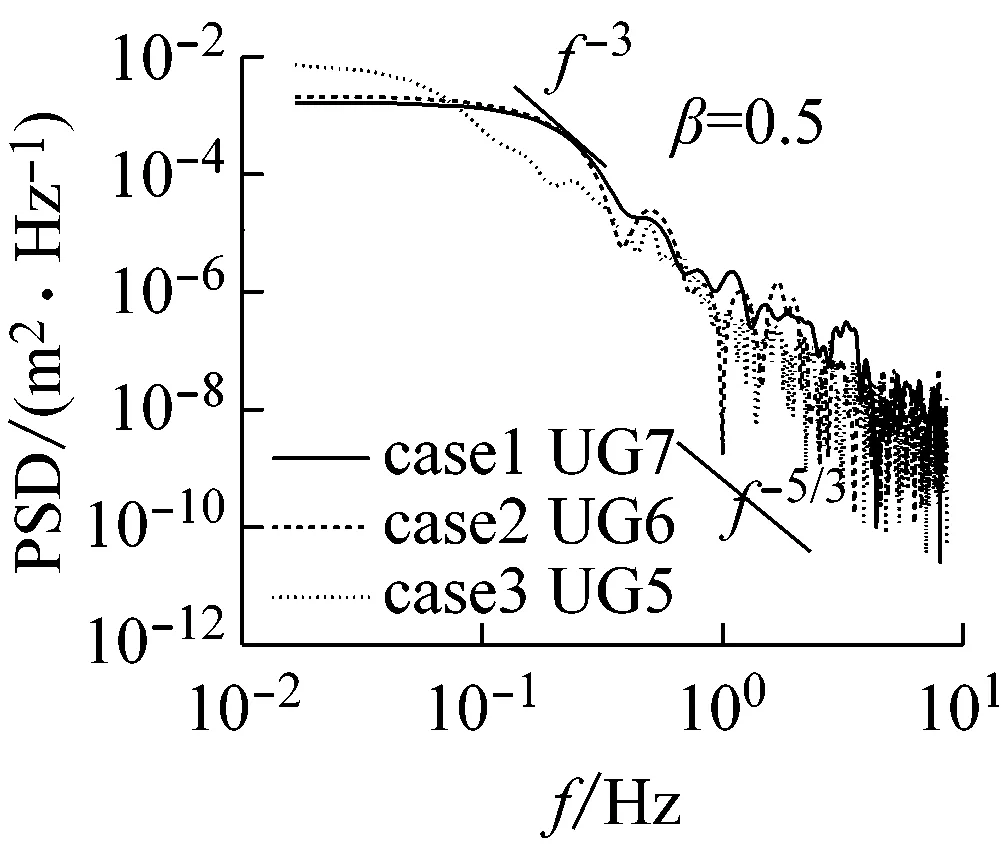
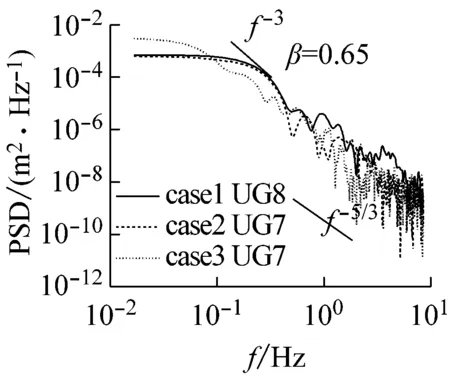
选择破碎区至冲流带岸滩不同断面的波浪进行时间序列分析,以期进一步揭示波浪对岸滩作用能量的分析。图7(a)为3个工况下相同无量纲化断面的功率谱密度图。当β相同时,各工况波浪特性呈现一定的规律性,三者的能量随频率变化的趋势基本保持一致,但在低频段,坡度越缓,离岸处的亚重力波的能量越少,在冲流带内却相反,表明坡度越缓,在冲流带内亚重力波占主导。图7(b)为相同工况、不同断面的功率谱密度对比图,可见沿岸滩向岸方向,功率谱密度整体有下移趋势,且区分显著,表明由于动能的减少以及床面阻力的作用,能量逐渐减小。
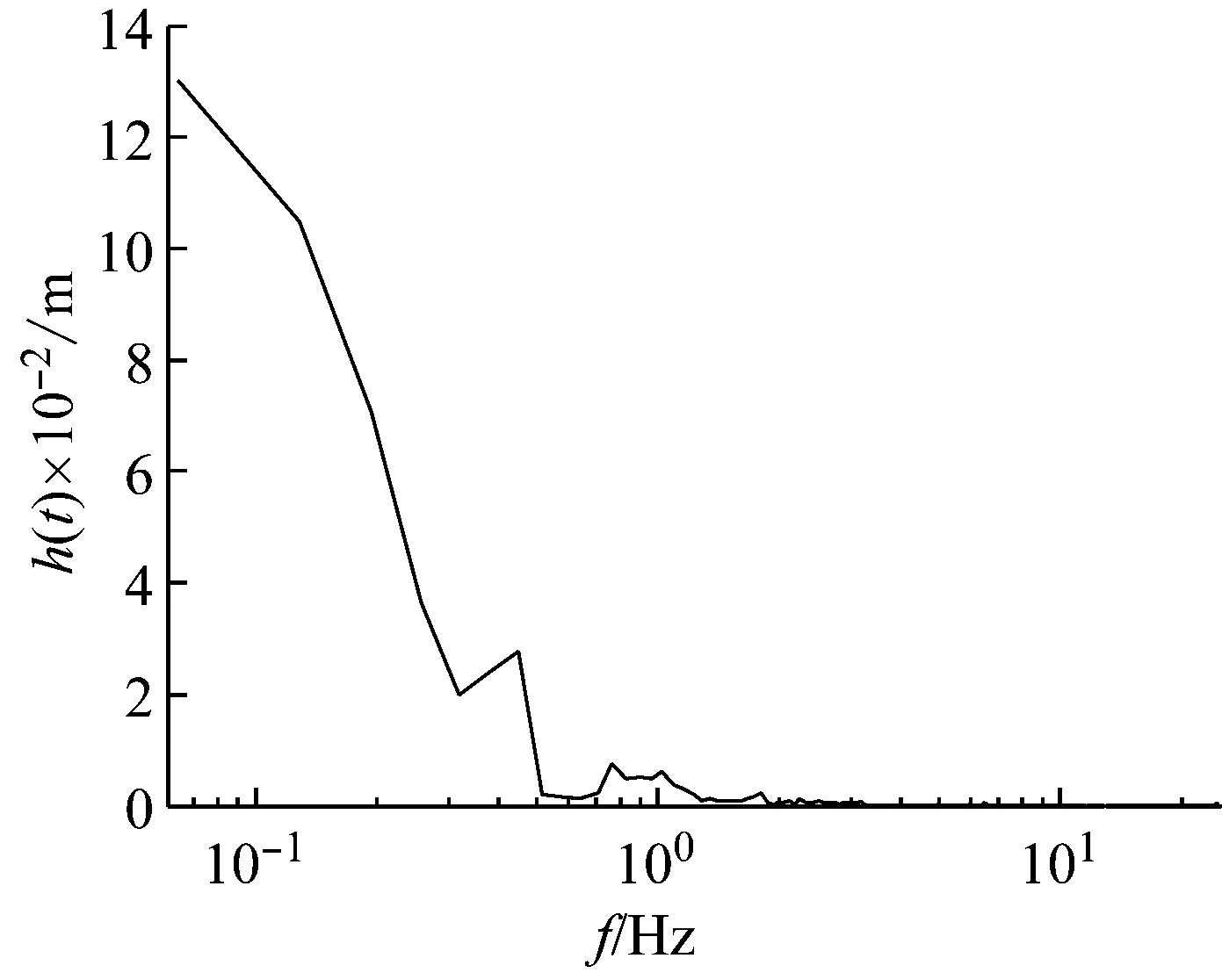
(a)Hilbert边际谱
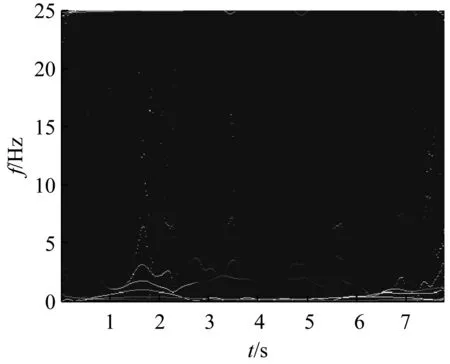
(b)Hilbert谱图6 Hilbert边际谱和Hilbert谱Fig.6 Hilbert marginal spectrum and Hilbert spectrum
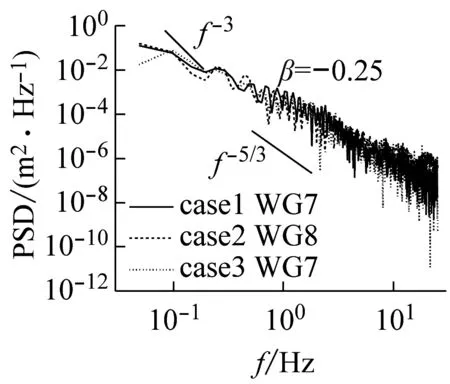

(a)


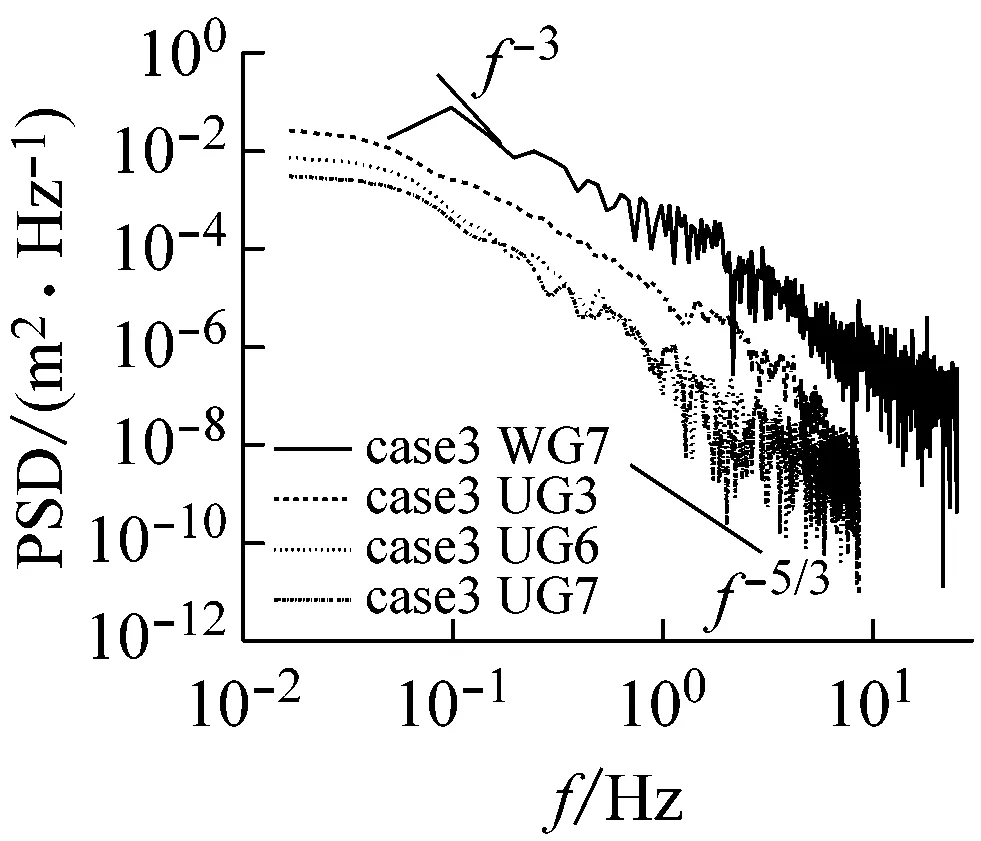
(b)图7 不同断面或者不同工况下的功率谱密度图Fig.7 Power spectral density diagram in different cross sections or under different conditions
与此同时,在低频处2个峰值能量之间出现了一个较小能量,此能量对应的频率为亚重力频率的截断频率,因为测量位置的不同,亚重力波的截断频率会有差异。采用类似Nakamura等[30]区分重力波和亚重力波的方法,一般取亚重力波频域介于0.03~0.3 Hz。当波浪频率极低时,即f<0.03 Hz,能量随频率的增大基本保持不变。当0.03 Hz
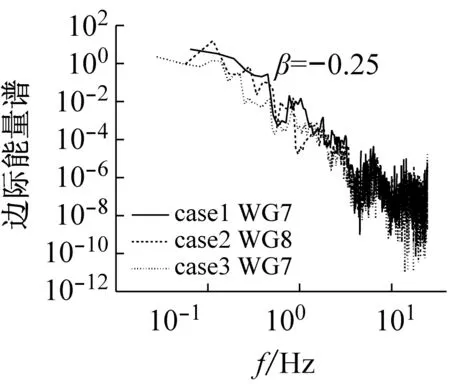
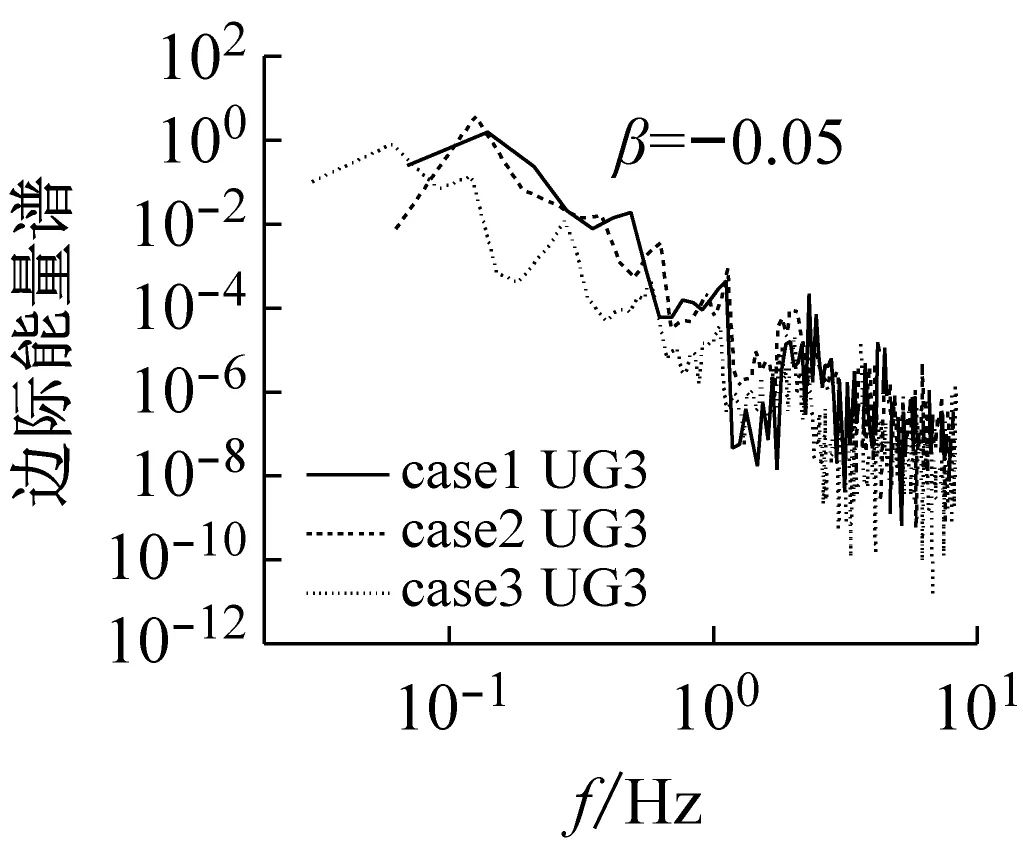
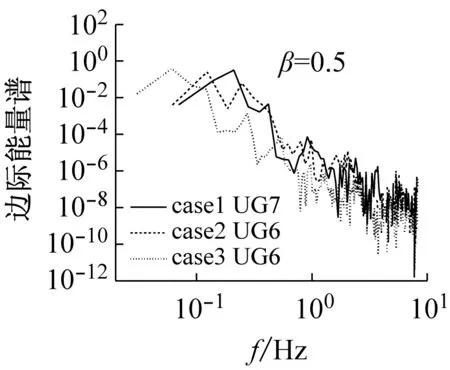
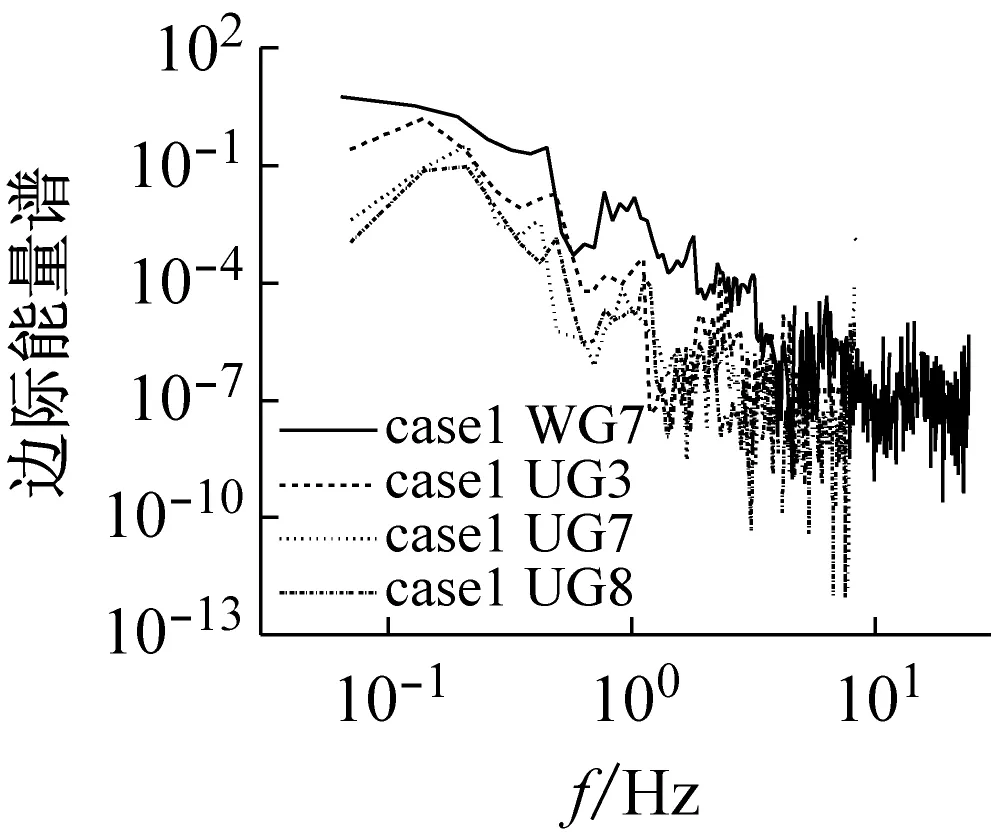
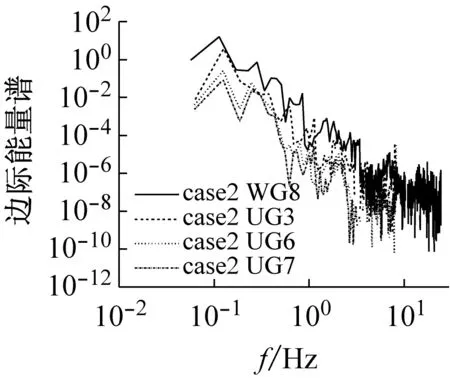
某一频率处的幅值代表整个时间轴上可能有这样一个频率的振动波在局部出现过,幅值越大表明该频率振动波出现的可能性越大(见图6)。除去端点效应的影响,在低频段内能量出现的频率很大,可认为该波浪信号是窄频带信号。图8是边际谱幅值的平方对时间的积分所得,表示某一瞬时频率信号的能量大小,并且边际能量谱和边际谱最大值所对应的频率是一致的,直观地反映频率和能量之间的关系。结合图6(a)与图8可知,低频带边际能量值较大,随着频率的增大,能量值逐渐减小,再次表明能量主要在低频段内聚集。这与前人野外观测结果符合,同时前人指出泥沙颗粒在此情况下极易发生运动,从而造成对岸滩的冲刷,同时高频带重力波会引起岸滩悬沙的输运[33-34]。
(a)
(b)
(c)

(d)
(e)
(f)

(g)图8 不同断面或者不同工况下的边际能量谱Fig.8 Marginal energy spectrum in different cross sections or under different conditions
波浪与岸滩相互作用的振动模式上能量随时间尺度存在一定的变化,一般把|X(t)|2看成是信号的能量密度,经过HHT变换后的H2(ω,t)也相应地具有能量密度谱的意义。忽略残差res,根据HHT变换前后能量守恒,则有
(9)
根据式(9),进一步得出波浪幅值所有频带内能量随时间的变化
(10)
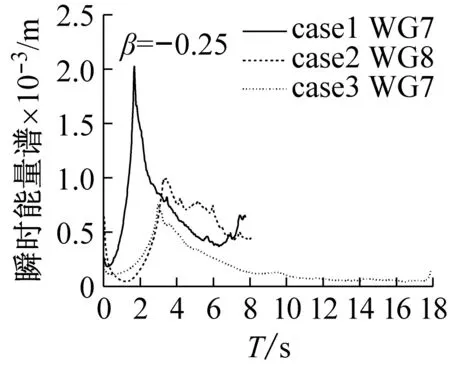
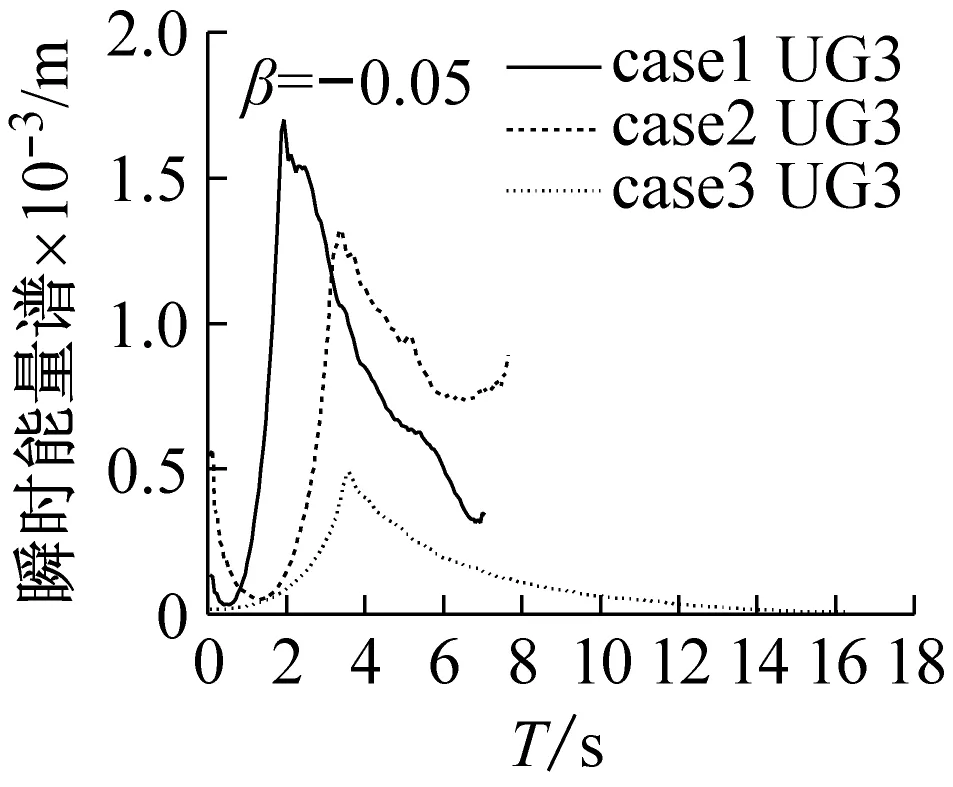
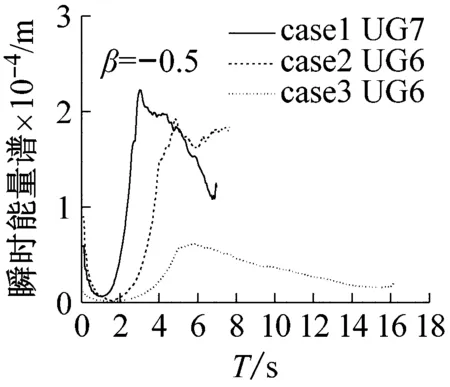
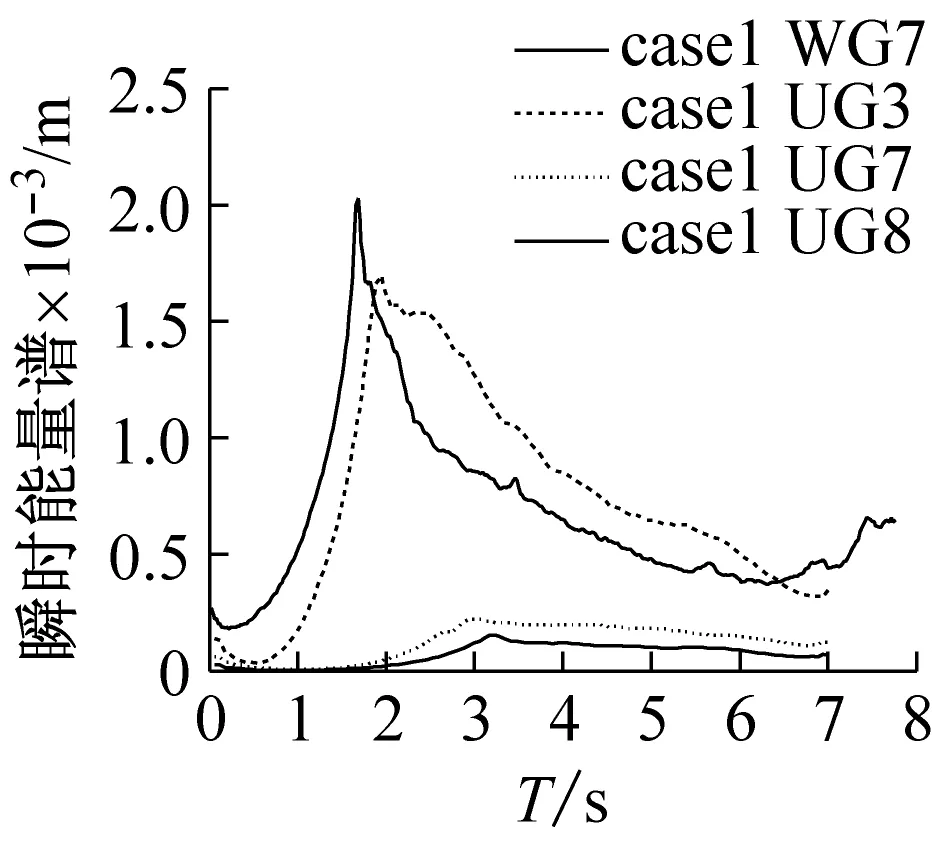
图9为不同断面在整个频域内能量随时间的变化,波浪抵达岸滩时,作用于断面的能量在很短时间内达到最大值,然后又迅速下降。能量达到最大值所用的时间比下降时间短,整体上瞬时能量均呈现先增加后减小的趋势,而瞬时能量的最大值与首次泥沙的起动有关。从本试验单一坡中可知,越靠近岸线位置,瞬时能量的最大值出现的时间越晚。而在组合坡中(case 2),由于坡度突然变陡,波浪与岸滩的作用增加,UG3断面的瞬时最大值能量变大,且大于前一个断面WG8。整体而言,3个工况的最大瞬时能量呈现随坡度的增加而增加,不同工况下最大瞬时能量出现的时间如表4所示,与原始波形记录(见图3)能较好对应,说明坡度越大,最大瞬时能量值出现的时间越早,对床面的作用也就越大。
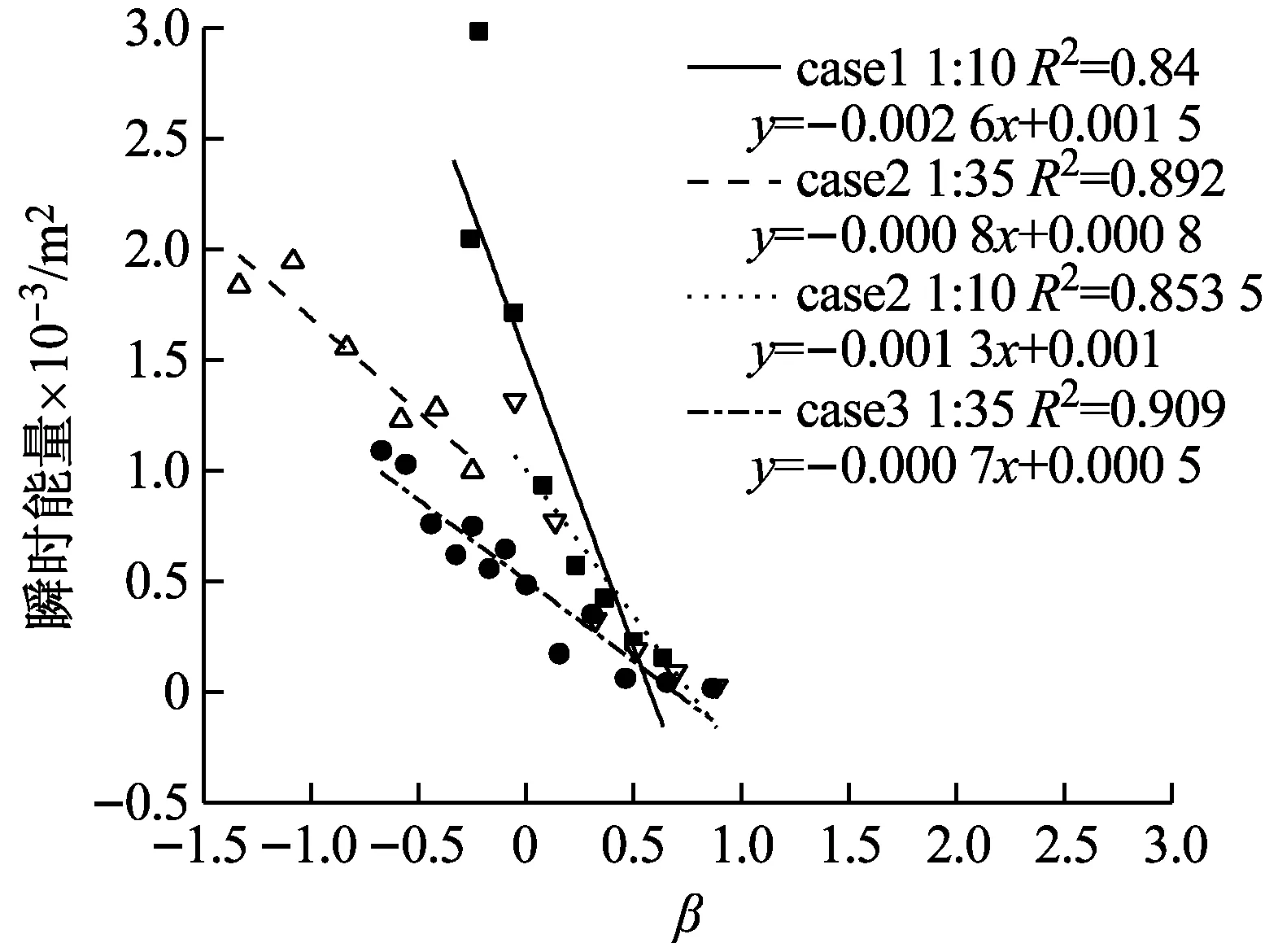
图10为各工况下岸滩断面与所对应的波浪最大瞬时能量的关系,计算R2(决定系数)与趋势线,case 1和case 3为单一坡,每个工况下各瞬时最大能量点拟合成一条趋势直线,case 2为组合坡,以2个斜坡的交点为分界点,拟合成2条不同的趋势直线。3个工况下瞬时能量最大值与断面位置均呈线性递减关系,且相关系数R2均较好。不同工况下的趋势线反映了不同断面瞬时能量的最大值沿着岸滩向岸方向逐渐减小,由此可推断床面受到的作用在破碎区与冲流带的交汇处(Rx=0)最大,可用于将来进一步分析动床下床面泥沙的运动。
(a)
(b)
(c)

(d)
(e)

(f)

(g)图9 不同断面或者不同工况下的瞬时能量谱Fig.9 Instantaneous energy spectrum in different cross sections or under different conditions表4 不同工况下瞬时能量最大值历时Tab.4 Maximum value duration of instantaneous energyunder three conditions

工况冲流时间/s坡度瞬时能量最大值历时/scase 17.61∶102~3case 28.61∶35/1∶103~5case 317.51∶353~6
对测量断面的瞬时能量进行求和,可得到该断面的总能量(见图10(b))。首先在整个冲流过程,case 1、case 2和case 3的能量变化基本保持一致,受岸滩床面的作用,沿岸滩向岸方向对断面作用的总能量逐渐减小,最后基本维持在0附近。其次,坡度越陡,总能量减少的越快,历经冲流过程所用的时间越短。冲流过程中总能量的变化表明岸滩一直受波浪影响,在初始岸线附近,波浪紊动剧烈、总能量较大,会产生较大的作用力,易导致床面受力平衡被打破,这在一定程度上解释了蒋昌波等[35]试验测量发现初始岸线处泥沙易起动。在β=0.65,即越趋近于高冲流带位置,总能量越接近为0,表明此处波浪作用力相对较小,可推断在动床下上易导致泥沙颗粒沉积在此处,符合前人观测到的试验结论[36]。此外,不同坡度下,组合坡前坡(1∶10)虽与case 1有部分岸滩重叠,但瞬时能量大于case 1(见图10(a)),而总能量却与case 1(1∶10)基本一致。这表明在组合岸滩中,瞬时能量与岸滩前坡关系密切,呈现波浪作用在与前坡坡度相同的单一坡度岸滩上基本一致的趋势,且能量主要集中在低冲流带区域(β<0)。综上可见,涌浪传播到近岸冲流带破碎后其水动力特征呈现高度的非线性,岸滩上波浪的能量耗散与岸滩坡度关系密切,在现实复合岸滩上(即组合坡度)波浪的非线性波动特性更为复杂。
(a)

(b)图10 不同工况下瞬时能量趋势和不同工况下总能量变化Fig.10 Instantaneous energy trend under three conditions and total energy change under three conditions
3 结 论
(1)通过EEMD分解冲流带试验波浪信号,得到多个IMF分量及其趋势分量,其中IMF7的方差贡献率为65.74%,为试验工况下波浪的主要成分,其对时序变化的影响程度很强。不同工况下波浪在一次冲流过程存在几个短期的周期性作用。
(2)冲流带波动能量主要由低频波段支配,约小于1 Hz。在低频段,坡度越缓,离岸处的亚重力波的能量会越少,而在冲流带内亚重力波占主导。当0.03 Hz
(3)岸滩坡度越缓,最大瞬时能量出现的时间越晚,最大瞬时能量值越小,对床面的作用越小,相应地向亚重力波转移的能量也随之减少。在本实验3个工况下,不同断面瞬时能量的最大值沿着岸滩向岸方向逐渐减小,波浪对岸滩作用2~3 s,3~5 s,3~6 s时接近波浪最大能量,且能量主要集中在低冲流带区域(β<0),可用于进一步分析岸滩的泥沙运动。
(4)各工况下沿岸滩向岸方向对断面作用的总能量逐渐减小。坡度越陡,总能量减少的越快,历经冲流过程所用的时间越短。初步发现在组合岸滩中,瞬时能量与岸滩前坡关系密切。
本研究应用EEMD和HHT方法对涌浪作用下冲流带波动特性开展试验研究,揭示了不同岸滩岸滩坡度下波动特性呈现不同周期性变化及其与能量的内在关系,但仅考虑了特定坡度范围内及定床条件,更多样的岸滩坡度及动床条件的研究有待进一步开展,以便冲流带泥沙输运的研究提供理论基础。
