商用车免维护轮毂轴承单元中间密封结构分析

2018-11-21鲁俊安徽华菱汽车有限公司

安徽科技 2018年7期

◎文/鲁俊（安徽华菱汽车有限公司）

商用车驱动桥免维护轮毂轴承单元在使用中，有相当比例的产品，会因为中间桥包的齿轮油通过轴承单元两个内圈之间的接缝处流入轴承内部，导致轴承单元早期失效。因此有必要为其设计开发可靠的中间密封，以有效阻挡齿轮油的进入。

一、商用车驱动桥轮端结构

商用车驱动桥中间带有一个装有减速机构的桥包，包内盛有齿轮油。车辆行驶时，桥包中减速机快速运转的同时，也将齿轮油飞溅到轴管中。由于商用车轮毂轴承单元是外圈旋转，且与车轴间隙配合，因此在轴的下表面与轴承内径间会出现间隙，而顺着轴管流淌的齿轮油在轴端流出后，可能会流入这个间隙，进而通过轴承单元两个内圈间的接缝流入轴承内部，见图1。

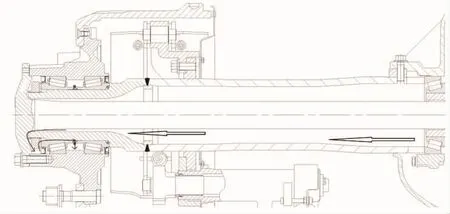
图1 齿轮油进入轮毂轴承单元的路径

二、免维护轮毂轴承单元及其中间密封的结构分析和研究

1.中间密封结构设计

首先设计了方形密封橡胶环结构，见图2（1）；为了减小橡胶环在密封安装被夹持时，大塑性变形引起的材料堆积的影响，在其加持带的上方设计有一圈凹槽，即结构1，见图2（2）；考虑到橡胶环的径向滑移，又设计了燕尾型底面的橡胶圈即结构2，见图2（3）。需要对图2（2）、

（3）两种结构设计进行对比。

图2 中间密封结构设计

2.中间密封材料选择

由于商用车轮毂轴承单元工作载荷大，并且经常是长时间连续运行，工作温度较高，因此需要采用氟橡胶材料制造。橡胶的硬度不宜太高，否则易老化；但是太低，密封接触力可能不足。选择邵氏硬度在70HA、75HA和80HA的三种材料进行接触应力分析。

3.中间密封接触力分析

由于中间密封圈材料为橡胶材料，可近似认为不可压缩超弹性材料。在实际应用中，橡胶材料存在着复杂的边界条件和接触非线性等各种问题。橡胶材料的非线性主要体现在以下几个方面:材料应力应变非线性、几何应变位移关系非线性及接触非线性，其中，橡胶材料的材料应力应变非线性可用应变能函数来表示[1]。还应当指出的是，橡胶材料在变形保持不变条件下，由于材料的粘性而使应力衰减（称为松弛）或者在载荷保持不变条件下，由于材料粘性而使变形继续增加（称为蠕变）又使得密封圈力学模型可能成为依赖于时间的粘弹性问题。为简单起见，本次仿真分析中并未考虑松弛及蠕变的影响。

近似不可压缩的橡胶材料的力学模型表现为复杂的材料与几何非线性。大部分学者都曾经提出过一些专门描述橡胶材料应力应变关系的函数，如Mooney-Rivlin模型、Ishihara-Zahorski模型、Klosner-Segal模型、Biderman模型等。为了能够配合使用ANSYS有限元分析软件中的有限元程序对所要求的问题进行求解，本次仿真分析中将会使用Mooney-Revlin模型[2]。在有限元分析中，采用完全Lagrange格式的增量分析方法来解决密封圈的几何非线性问题，即在分析过程中，所有静力学和运动学变量总是参考（始终保持不变的）初始位形，具体分析方法可参考文献[3]。分析中采用的橡胶材料模型为近似不可压缩弹性材料的Mooney-Rivlin模型[4]，和材料的应变能偏量部分有关的两个材料常数C10和C01（常称之为穆尼材料常数）可由从实验获得的经验公式[5]中根据橡胶材料的硬度（或弹性模量）计算得出，两个参数的Mooney-Rivlin方程为

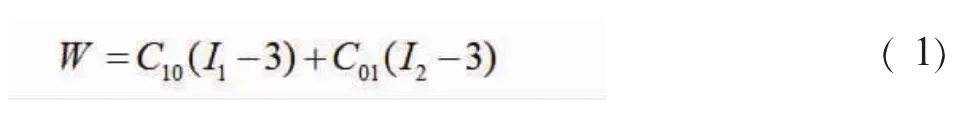
式（ 1）中，C10和 C01是 Mooney 常数，I1、I2为第一、第二Green应变不变量。

在小应变时，橡胶材料的弹性模量E0与剪切模量G的关系如下：

由橡胶材料的不可压缩性得泊松比μ=0.5，于是E0=3G，得到

根据橡胶材料IRHD硬度Hr与E0的实验数据，经拟合得式：

再结合C10、C01的经验比值，就可确定材料系数C10、C01的值。本项目中所用不同硬度的橡胶对应的C10、C01的计算数值如表1、表2所示。

表1 不同硬度的橡胶对应的C10、C01的计算数值

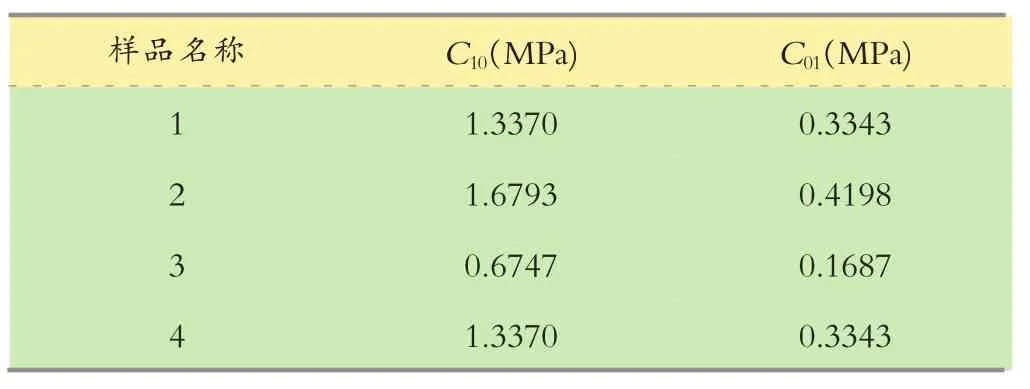
表2 不同样品对应的C10、C01的计算数值

4.建立边界条件

模型的基本假设。为了有限元分析能够顺利进行并取得近似准确的结果，本次仿真分析对材料的性质以及边界约束等情况进行如下假设：制成密封圈的橡胶超弹性材料的弹性模量E和泊松比μ的值一定；密封圈及接触边界可以认为是轴对称；密封圈的橡胶材料具有不可压缩性；由于套圈的刚度是橡胶刚度的几万倍，所以套圈可以被认为是刚体边界[6]。

建立有限元模型。在密封结构中已经不能通过线性理论描述橡胶材料在受力情况下的位移和变形关系，就需要通过几何非线性理论来解释。利用ANSYS有限元分析软件的扩展命令功能，再加上密封圈的边界受到的力具有圆周对称性，以及考虑到密封圈的特殊结构，可以将密封圈模型简化为轴对称的平面模型。通过ANSYS有限元分析软件中的扩展命令对得到的分析成果进行扩展，就可以达到和三维模型进行分析的相同效果。另外，本次仿真分析主要是在静态分析的条件下对密封圈模型进行分析的。本次仿真分析所用的模型根据图2（2）、（3）两种结构进行创建。选用两种样品，其中样品1和2采用分析模型（1），样品3和4采用分析模型（2）。

边界条件和载荷。由于密封圈与套圈之间是过盈配合，因此在建模时要使二者平移至恰好接触，在对安装过程进行模拟时，只需给套圈一个轴向方向和径向方向的位移，其大小恰好是过盈量Sx和SY，不同样品接触条件下的过盈量以及对应的分析模型见表3。

表3 不同样品接触条件下的过盈量

5.中间密封的理论验证评价

通过建模，得到了轴向密封接触力分布、径向密封接触力分布和整体FEA应力分布云图（图略）。从图中可见，四种样品的轴向最大值分别为31.31N、20.72N、7.8N、15.35N。四种样品的径向最大值分别为4.85N、3.12N、1.98N、3.93N，接缝处径向分别为 3.77N、1.73N、1.98N、3.93N。

分析结果表明，样品1型密封的径向接触力分布不是均态，在接缝处的接触力为3.2N，没有漏油发生；样品2型密封的径向接触力分布也不均匀，在接缝处的接触力为1.3～1.7N，发生漏油；样品3型密封的径向接触力分布均匀，在接缝处的接触力为1.98N，可能发生漏油；样品4型密封的径向接触力分布均匀，在接缝处的接触力为3.93N，不可能发生漏油。