高等数学中的类比思维
2018-11-19牛应轩王东明傅传秀
牛应轩,王东明,傅传秀
(皖西学院 金融与数学学院,安徽 六安 237012)
创新能力是国家竞争力的核心,党的十九大对创新创业人才培养做出了重要部署,国务院对加强创新创业教育提出了明确的要求。创新是当今的时代精神,高等学校担负培养创造性人才,培养出更多创新型人才的重任。高等数学是各理工科专业重要的基础理论课,其目的在于培养工程技术人才所必备的数学素质,为培养我国现代化建设需要的高素质人才服务。一方面,高等数学是学生专业知识学习的基础和重要工具。另一方面,高等数学的理论和方法对学生创新能力的培养及综合素质的提高有重要意义。它是培养学生的创新思维和创新能力的有效工具和重要途径。创新能力的形成很大程度上取决于人们的创造性思维方式,创造性思维是一切创造性活动的核心和灵魂。
高等数学涉及许多的思维形式,如抽象思维、逻辑思维、形象思维和猜想思维等等[1](P14),它也包含了多种思维方式,例如变量函数思维方式、无穷分析思维方式、相似类比思维方式、反例反驳思维方式和空间想象思维方式等等[1](P68)。本文我们讨论高等数学中的类比思维。所谓类比,就是借助于两类不同本质事物之间的相似性,通过比较将一种已经熟悉或掌握的特殊对象的知识推移到另一种新的特殊对象上去的推理手段。一方面,类比思维和类比推理是高等数学中常用的数学思维和数学推理,它提供了高等数学的学习方法,也为理解和掌握高等数学中的概念、定理及公式提供帮助。它能够将不同层次的类似内容串联一起,帮助记忆。另一方面,类比思维还大量应用到科学技术的发明创造上,例如潜水艇的设计思想来自鱼类在水中浮沉的生物机制的类比;蜜蜂的太阳偏光定向的功能,启发人们制造了航海偏光天文罗盘等等。我们通过例子说明类比思维的几种表现形式,显示它在培养创新意识、创新思维和创新能力中的作用。
类比的认识论根源就是思维相似律,也就是客观事物发展过程中的相似现象在思维过程中具有相似的反映,它是人的思维的一个基本规律。著名日本物理学家、诺贝尔奖获得者汤川秀澍(Yukawa,1907—1981)说:“类比是一种创造性思维的形式”[2]。类比为人们的思维过程提供了更广阔的“自由创造”的天地,使它成为科学研究中非常有创造性的思维形式。
1 平面与空间的类比
著名数学家、教育家波利亚(George Polya,1887—1985)说:“类比是一个伟大的引路人,求解立体几何问题往往有赖于平面几何中的问题。”[2]由条件的相似性可以推得相似的结论。这在平面与空间的类比中尤其明显。

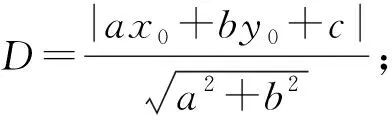

类比是提出新问题和作出新发现的一个重要源泉,通过平面解析几何与空间解析几何的类比,在学习高等数学中的空间解析几何时,可以由熟悉的平面解析几何的知识比较容易、自然地掌握空间解析几何中的新结论。
2 抽象与具体的类比
抽象性是数学的特征之一,抽象的问题是学生在学习高等数学中遭遇到的最大的困难。如果我们能够将抽象的问题与具体的问题进行类比,发现抽象问题与具体问题的相似性质,从而利用具体问题的性质得到抽象问题的解决。这样就为学生排除学习中的困难,能够极大地激发学生的学习兴趣和积极性。
下面我们展示如何利用类比方法解决在极限理论中无穷大的问题。无穷大是一个抽象的概念,它是什么?它与通常的数有怎样的联系与区别?是学习高等数学中一个必须要解决的问题。首先我们知道数与实数轴上的点有着一一对应关系。我们想象有这么一个点称为无穷远点或称为“理想的点”,它是实数轴的两端的“交点”,记为∞,如图1。

图1 无穷远点的定义
对于数轴上的点x0的δ-邻域的几何表示如图2。
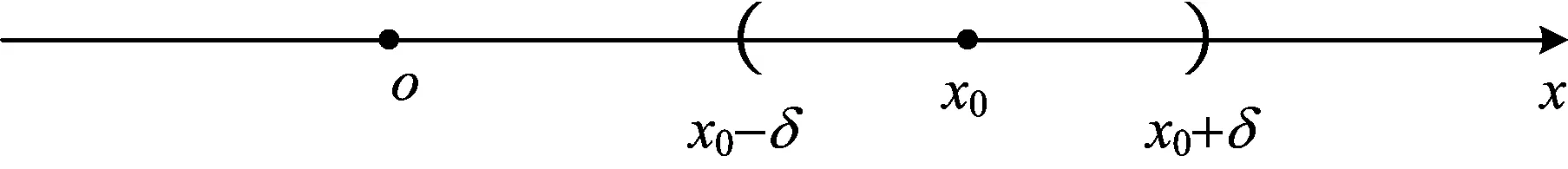
图2 x0的δ-邻域
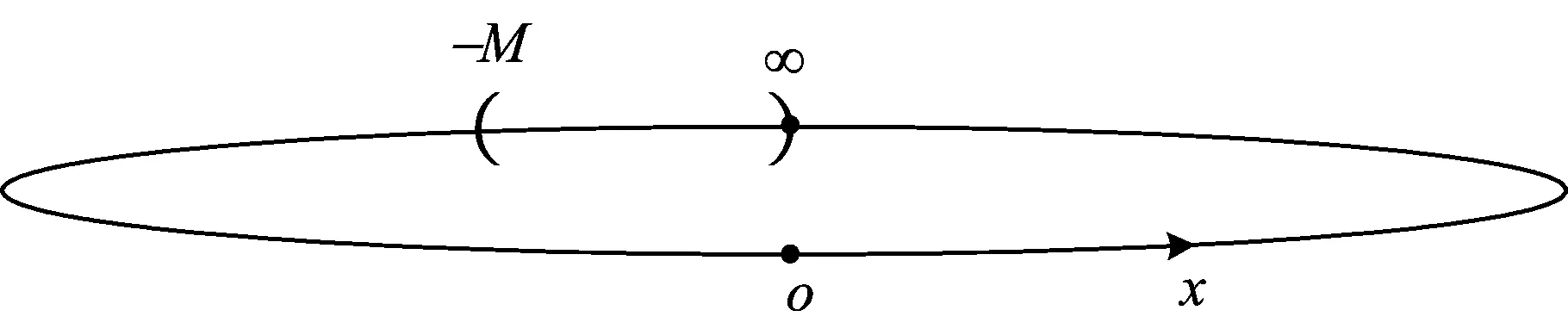
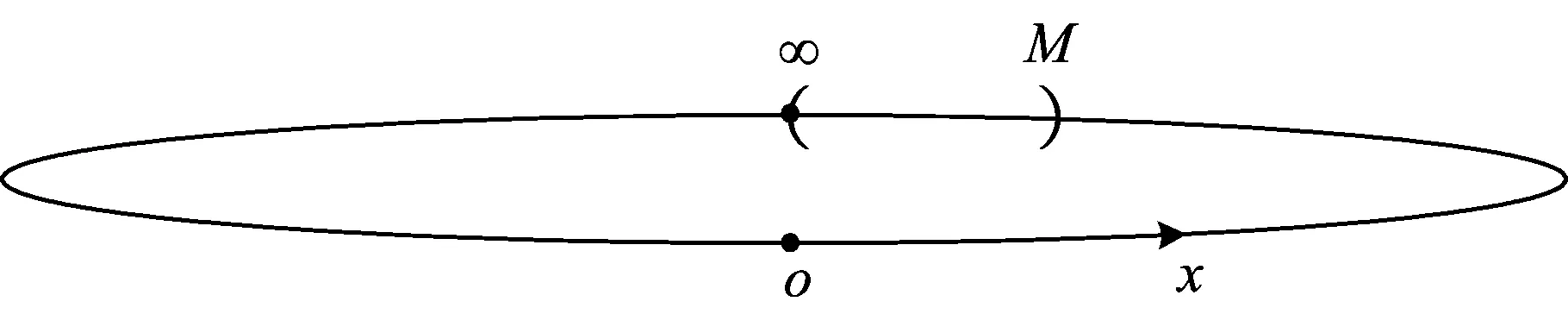
它的代数表示是U(x0,δ)={x|x0-δ 图3 无穷远点的M-邻域 从而它的代数表示是U(∞,M)={x||x|>M}。数轴上的点x0有邻域与去心邻域之分,而无穷点∞的邻域与去心邻域是一样的。数轴上的点x0有左、右δ-邻域,其相应的几何表示如图4、图5。 图4 x0的左δ-邻域 图5 x0的右δ-邻域 类比数轴上的点x0有左、右δ-邻域,我们可以得到∞的左、右M-邻域,其相应的几何表示如图6、图7。 图6 无穷远点的左M-邻域 图7 无穷远点的右M-邻域 它们分别称为-∞(+∞)的M-邻域,其代数表示是U(-∞,M)={x|x<-M}和U(+∞,M)={x|x>M}。 我们记Θ为x0或x-或x+或∞或-∞或+∞,Ξ表示常数A或∞或-∞或+∞。因此,利用类比思想和方法,由上述的极限的定义,我们可以在统一的观点下,给出各种极限的统一定义: 有很多实际问题的精确解,仅仅通过有限次的运算是求不出来的,而必须通过分析一个无限变化过程的变化趋势才能求得,微积分的建立就是这种思想。我们已经掌握了初等数学的方法和一些结果,它们能够解决有限的问题,那么在解决和分析无限的问题时,可以通过类比思维方式给予解决。辩证法告诉我们量变到质变规律,因此由有限到无限时仅仅通过简单和形式上的类比得到的结果未必正确,这是需注意的问题,可以通过对结果进行修正而得到正确的结果。 高等数学的主要研究的内容是一元函数的微积分和多元函数的微积分。在掌握了一元函数的微积分知识基础上学习多元函数微积分时,类比思想和方法起到非常重要的作用和效果。通过已学知识和新知识进行类比,更容易接受、掌握和理解新知识。 一元函数有极限、连续、导数和积分的概念,而对于多元函数相应地有极限、连续、偏导数和重积分的概念。 一元函数的定积分是通过要计算曲边梯形的面积而引入的,利用微元法的思想,通过“分割”“近似”“求和”和“取极限”四个步骤给出定积分的定义。类比一元函数的定积分,要计算曲顶柱体的体积,同样通过“分割”“近似”“求和”和“取极限”四个步骤给出二重积分的定义。 对于一元函数的极限、连续、导数和定积分都具有线性性质,类似地,对于多元函数,极限、连续、偏导数和重积分也都具有线性性质。 类比闭区间上的一元连续函数具有有界性、最值性和介值性等性质,有界闭区域上的二元连续函数也有有界性、最值性和介值性等性质。 类比思维的认识依据是客观事物和对象之间存在的普遍联系-相似性,因此,“类比就是一种相似”[3](P38)。相似律的主要内容之一是相似的基因、相似的条件和相似的环境产生相似的结果。由于一元函数与多元函数在相应的概念上具有较强的相似性,因此在性质和结论上具有许多的相似性就不足为奇了。 类比推理是一种“合情”的“似然”推理,它的正确性不能肯定,原因在于:在推理过程中使用的“相似”这个概念,本身不是确定的,有很大的变化范围,人们可以给出各种各样的“相似”,况且“相似”毕竟有差异,因此,类比推理中的前提与结论的从属关系不是必然的,而是或然的,其正确性必须加以证明或举反例来判定。 例如在一元函数微分学中有“如果函数f(x)在x0处可导,那么f(x)必在x0处连续”的结论[4](P85),通过类比,我们可以得到在二元函数微分学中有结论“如果函数f(x,y)在(x0,y0)处有偏导数,那么f(x,y)必在(x0,y0)处连续”,但是我们可以给出反例说明该结论是不正确的[5](P67)。虽然上述的类比结果是不正确的,但是它仍然是符合类比推理规律的一个结果。我们从中可以看出其思维的意义,即引导我们修改类比的设想和结果,直至得到正确的结果。在高等数学的多元函数的微积分中,有许多这种情况。 德国哲学家康德(Kant,1724—1804)说:“每当理智缺乏可靠论证的思想时,类比这个方法往往指引我们前进”[6](P204)。类比思维在数学知识延伸拓广过程中常借助于比较、联想用作启发诱导以寻求思维的变异和发散。在归纳知识系统时又可用来串联不同层次的类似内容,以帮助理解和记忆。在解决问题时,是产生新成果的原动力。本文讨论的类比思维的几种形式和例子富于启迪性,它们说明类比思维和推理可以启发思维,提供线索,举一反三,触类旁通。因此,类比方法既是数学学习的重要方法,也是数学发现的有效途径,因此予以充分地重视是十分必要的。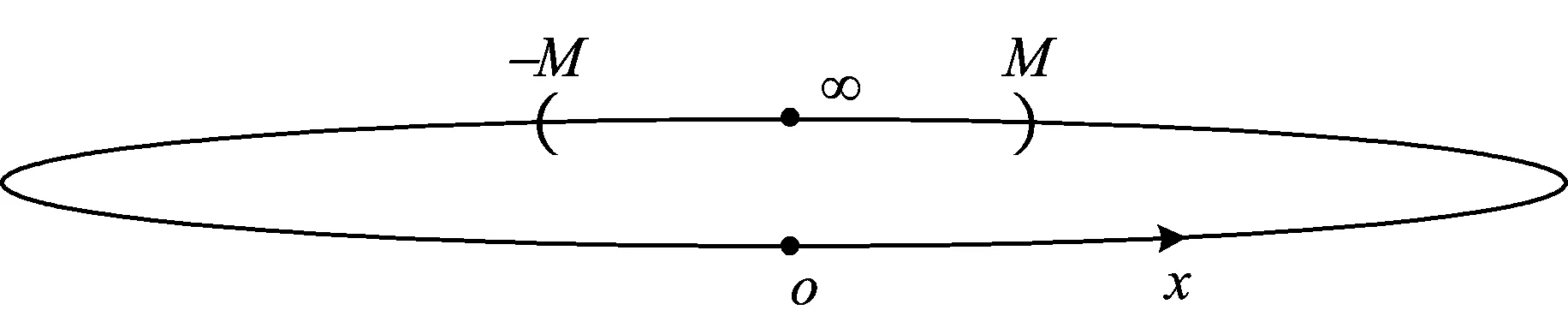

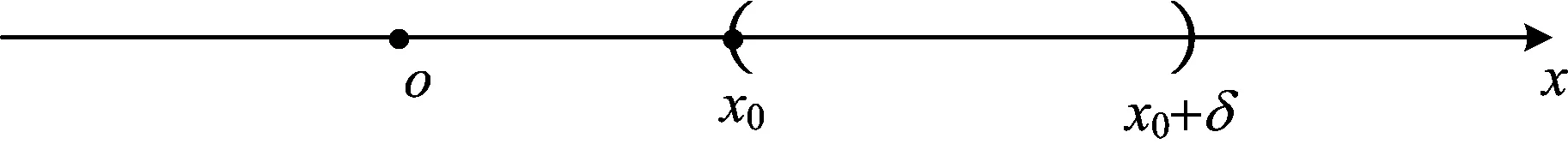
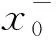

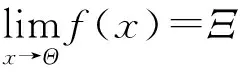
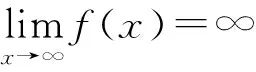

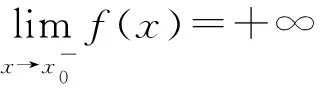
3 有限与无限的类比
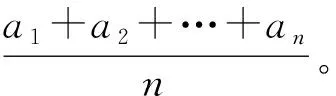
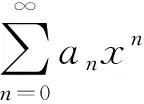
4 低维与高维的类比
4.1 概念的类比

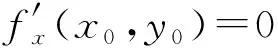
4.2 性质和结论的类比

