基于RNN的心电信号异常检测研究

李锋，王泽南

（东华大学计算机科学与技术学院，上海 201620）

0 引言

心电图（electrocardiogram，ECG）是记录心脏电信号的常用方式[1]，医护人员通过分析心电图数据，可以较为准确地判断心脏的健康状况。目前，大量的科研学者已经开始尝试采取计算机技术来分析心电图数据，从而实现在无医学监督下对个体心脏状况的实时监测。

1998年，Silipo R等人提出了用人工神经网络（Artificial Neural Network，ANN）的方法对三种异常的 ECG 信号进行分类[2]，他们采用了多种ANN 结构，配合不同的预处理方法，验证了ANN在面对ECG波形时具有良好的适用性。Lagerholm M[3]等人构建了自组织的神经网络实现ECG信号的无监督聚类，通过麻省理工心率失常数据库中16类心电数据进行实验，得到了较准确的分类结果。之后，Benali R[4]等人结合小波变换与神经网络对正常心电信号和4类异常心电信号进行了分类，也获得了较高的分类准确率。Acır N[5]等人提出了通过最小二乘支持向量机（Least Squares Support Veotor Maohine，LSSVM）的方法对ECG信号进行分类，该方法在对特征向量空间降维处理的基础上，用快速LSSVM算法对心电数据进行分类。在文献[6]中，Shen CP采用了一种自适应算法来提取数据特征，然后结合支持向量机（Support Vector Machine，SVM）和K均值聚类对样本数据集进行分类。

本课题组长期研究躯感网和机器学习，并设计出一种便携式心电采集设备,实现对心电数据的采集。本文主要在国际公开数据库和实验室采集的移动心电数据基础上,使用心电数据相邻点斜率和RNN相结合的方法，实现心电信号的异常诊断。

1 基于心电数据斜率的心电信号异常检测

为了便于通过神经网络实现对心电信号异常的自动诊断，系统首先需要分析心电数据的内在特性，提取特征序列作为神经网络的输入。心电信号特征提取目前已有众多成熟的算法，例如Palacios-Enriquez A提出基于小波变换的方法[7]；Soorma N提出了一种基于HHT变换的特征提取方法[8]。

由于这些变换算法会丢失心电数据本身的物理含义，本文选用相邻数据点斜率组成的数据串作为心电数据的特征，并将该数据串作为循环神经网络的输入。

1.1 循环神经网络

循环神经网络（Recurrent Neuron Network，RNN）可以很好地处理序列类数据。与一般的神经网络不同，循环神经网络除了层与层之间的全连接，还包含了前一个节点的输出对当前节点的影响，即隐藏层的节点不再是独立的，隐藏层输入包含输入层的数据和前一节点的输出[9]。隐藏层各节点都会受到之前节点的影响，为避免之前节点数据过度参与当前节点的计算，一般会引入遗忘率α作为前一输出的权重[10]。

本文后续实验的数据是基于矩阵转换而成的序列数据，该序列数据前后数据点存在关联性，因此利用RNN来处理该数据具有较好的适用性。

2 异常检测

2.1 算法流程

本文首先通过滤波等方式对心电数据进行预处理，然后计算相邻点的斜率并进行组合，形成特征序列输入到神经网络，完成异常检测。

本文神经网络的训练数据集来自Physio Bank数据库，共计1600条数据。根据该数据库中已标记的病理标签，本文将训练集数据标记为四类：正常、心肌梗塞、房室阻滞和房性早搏，四类数据各有400条记录。测试数据集使用实验室采集的共1491条用户数据，测试数据集包含正常242条，心肌梗塞398条，房室阻滞415条，房性早搏436条。部分实验数据如表1所示。

2.2 心电数据特征提取

在信号处理过程中，由于心电信号在采集过程中会受到工频干扰、基线漂移、肌电干扰、电极移动等因素的影响[11]，本文在进行心电特征提取前对数据进行了高斯滤波，避免噪声对心电数据特征提取的影响。

心电信号是一个多分量信号，为保证心电信号原本物理意义的完整性，本文选择提取相邻点斜率作为特征。每一时刻的斜率计算公式如公式（1）所示。

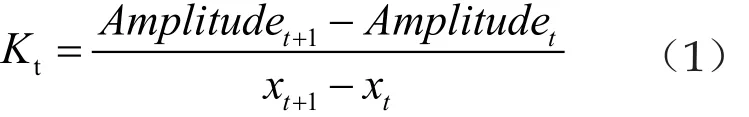
表1 原始心电数据表

表2 相邻点斜率结果表

2.3 数据组合

神经网络进行异常检测时，单一的斜率值无法作为神经网络的输入，因此需要将每一串斜率值进行拼接，即将每个斜率值按时序组合成一个一维数据串。以patient005为例，其组合结果如图1所示。此时的数据串包含斜率特征和时序特征，这样可以实现多维特征的异常诊断从而提升神经网络的诊断准确率。

图1 patient005一维数据串结构图

2.4 RNN网络

2.4.1 LSTM构建

本文选用长短期记忆神经网络（Long Short-Term Memory，LSTM）进行异常心电检测。LSTM在RNN基础上进行了改进，能更好的处理序列数据[12]。本文LSTM网络结构共分为三层：输入层、隐藏层和输出层，结构如图2所示。

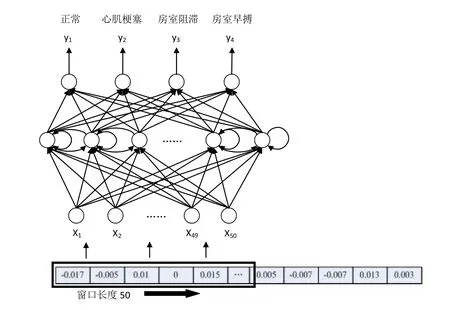
图2 神经网络结构图

网络的输出层4个节点分别对应类型心电图概率值。

针对输入层，通过实验得到节点数为50个时时间复杂度和空间复杂度在可接受范围，神经网络通过窗口滑动将数据串依次输入到节点进行计算。

隐藏层节点个数没有实际的参照标准，本文通过实验，将节点个数设置为60。隐藏层节点个数与准确率的对应关系如表3所示。

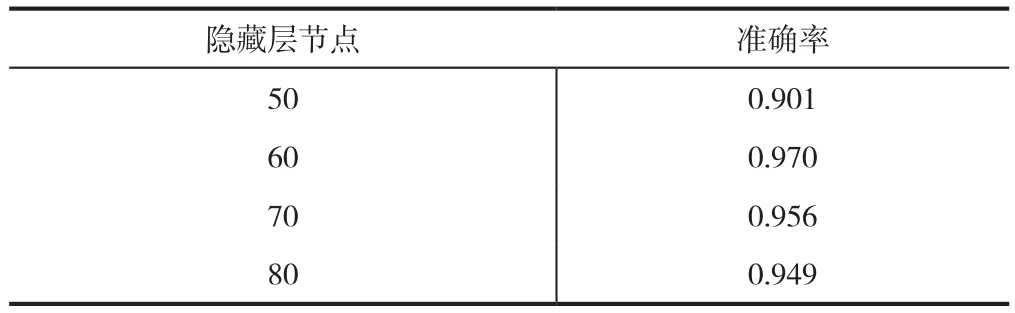
表3 隐藏层节点与准确率关系表

由于隐藏层前后节点互相连接，因此前一节点作为当前节点输入时的遗忘率亦会影响神经网络的学习效率以及分类结果。本文经实验分析后将遗忘率α设为0.75。遗忘率对实验结果的影响如表4所示。

表4 遗忘率与准确率关系表

在隐藏层通过公式2计算t时刻各个节点的状态。

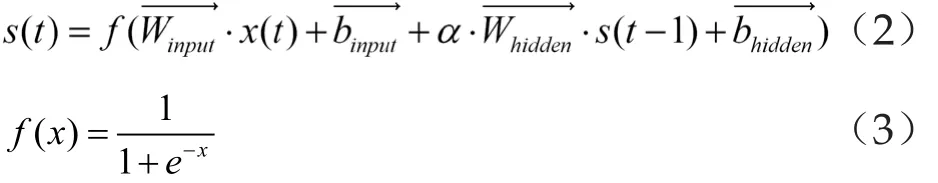
其中f(x)为激励函数，分别为输入层和隐藏层偏置，分别为输入层和隐藏层权重。

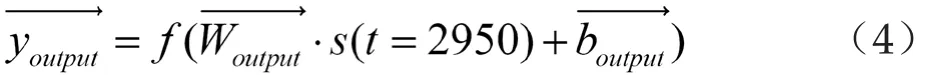
其中，s(t=2950)为隐藏层最终的节点状态，由于滑动窗口每次移动1个单位，故节点状态数=数据串长度-窗口长度+1=2999-50+1=2950，因此隐藏层节点最终状态为s(t=2950)。分别为输出层的权重和偏置。通过公式5将该结果转换为最终的输出结果

p1：待测心电属于正常的概率；

p2：待测心电属于心肌梗塞的概率；

p3：待测心电属于房室阻滞的概率；

p4：待测心电属于房性早搏的概率。

2.4.2 神经网络训练过程

在构建完成网络结构后，需要对网络进行训练，训练步骤如下：

Step1：初始化网络结构，将所有权重和偏置赋值为一个随机值；

Step2：读取一条心电数据输入到神经网络；

Step3：分别计算输入层，隐藏层和输出层的输出；

Step5：获得判别结果并计算损失函数。损失函数计算方法将在2.4.3节进行阐述；

Step6：根据梯度下降算法调整各个权重和偏置。

在神经网络训练过程中，重复Step2至Step6，当损失函数误差e≤0.001或训练集数据被遍历时，神经网络训练结束，将待测心电数据输入到网络中即可得到异常检测结果。

2.4.3 损失函数计算

本文使用真实病理标签对应节点的概率值计算损失函数，计算方法如公式6所示。

其中R为其病理标签对应节点的概率。例如，将某房室阻滞病人的心电数据传入神经网络，通过公式6和公式8计算得到再将得到的利用公式4进行计算：

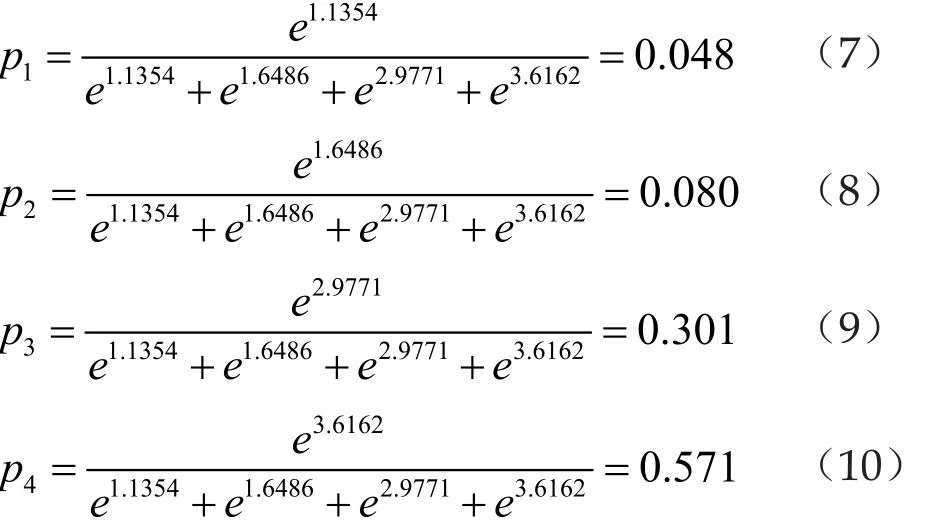
3 实验分析

本文根据准确率（CA）（公式11）评判实验的整体性能。

其中，Y表示检测结果正确的数据记录数量，T表示测试数据总数量。

本文对测试数据集的1491条记录进行分析，实验结果如表5所示。

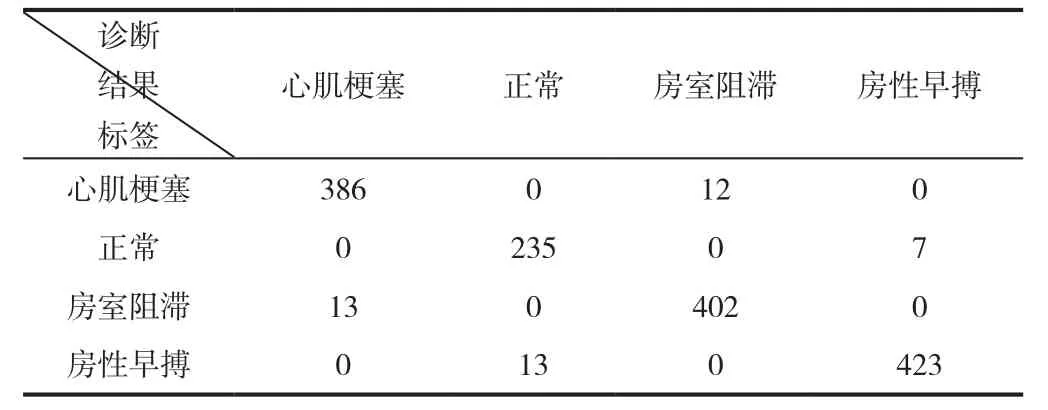
表5 病理判别结果表

由表5可知，心肌梗塞与房室阻滞容易产生误判，正常与房性早搏容易产生误判。主要原因为被误判的两类病理在早期心电数据上区别较小，虽经过PWD处理，但依然存在误判的可能性。经过计算，本文算法准确度可达97.0%，因此该算法具有一定有效性和实用性。

4 结束语

本文利用相邻数据点间的斜率进行拼接得到一维数据串，然后将数据串通过循环神经网络进行异常诊断，实验数据证明其分类效果良好，但对早期病理的数据仍存在误判可能，还需一些改进。本文实验只是针对四类心电异常进行诊断，课题组在此基础上还将针对各类病例的诊断进行进一步研究。