霍尔推力器羽流对太阳翼的溅射影响规律

2018-11-19，，，，*

中国空间科学技术 2018年5期

，，，，*

1. 上海空间推进研究所，上海 201112 2. 电子科技大学电子学院，成都 611731 3. 上海空间发动机工程技术研究中心，上海 201112

霍尔推力器羽流是一种由高速离子和电子组成的等离子体射流，是形成推力、电荷中和的主要区域，然而若羽流中介入任何悬浮物体时，必然会发生相应的质量、动量以及能量的交换，特别地，有些交换过程具有一定的破坏性。尤其在空间应用工况中，羽流对航天器的影响是不可忽略的。根据国外已有报道，羽流对航天器的影响主要表现在高速离子对各元器件表面的溅射作用[1-3]，尤其是光学敏感元器件太阳电池翼的表面，由于溅射对太阳翼表面材料二氧化硅具有一定的削蚀改性作用，可能导致透光率的降低，从而影响太阳翼对光能的吸收，降低卫星系统的能量供给量。

关于羽流对太阳翼的溅射影响，国内外已有一些报道：Randolph等[4]对SPT-100霍尔推力器羽流半径为1m的位置进行探针诊断，认为在该位置以外的区域，羽流对太阳翼的功率影响不会超过1%，而对翼板的溅射影响可以忽略；Fife等[5]研发了一个对羽流预估、优化设计的仿真平台COLISEUM，通过试验验证其计算精度后，对200W的霍尔推力器羽流进行了模拟，结果显示溅射对厚度的削蚀速率不超过6×10-12m/s；田立成等[6]对SPT-100霍尔推力器建立了束流计算模型以及卫星敏感区的理论模型，并利用该模型对SPT-100进行翼板布置角在30°～50°工况的数值计算，认为在45°布置后的溅射与沉积作用可以忽略。实际上，上述学者或是通过试验，或是通过仿真，均以少量工况的预估为主，给出了一些布置工况下的预估，虽然为溅射影响的分析提供了一定参考，但是上述工况覆盖并不全面，没有形成明显的变化规律，缺乏通用性，这对卫星快速调整推力器布置带来一定难度。为此，开展霍尔推力器羽流对太阳翼多种布置工况的溅射作用规律研究，以补充这部分研究的空白。

由于涉及大量在轨工况的预估，本文采用数值模拟的方法。以较为成熟的单元粒子/蒙特卡洛混合算法(PIC/DSMC)[7-9]对霍尔推力器羽流进行参数分布计算，需要说明的是，在该模型中引入离子扩散机制来进一步提升羽流输运过程的仿真精度，接着，结合鞘层电势模型和Yamamura模型[10-12]来对太阳翼表面的溅射作用进行模拟。

1 模型

首先针对本文所采用的主要物理模型和计算流程进行介绍，共涉及两个物理过程：等离子体输运过程和羽流-翼板相互作用过程。在等离子体输运过程中：

1)以PIC算法求解计算粒子在每个时间步长内的运动状态(力、速度、位移等物理参数)；

2)完成各个计算粒子的物理参数对周围节点的权重分配；

3)在完成运动状态的更新后，以DSMC碰撞模型对粒子间的碰撞过程发生概率及碰撞类型进行判断；

4)更新本时间步长内，部分发生碰撞的粒子的速度和加速度，以此来实现羽流中等离子体粒子的运动及碰撞过程的模拟。

在羽流-翼板相互作用过程中，以溅射模型来判断粒子在碰撞太阳翼后的运动状态以及计算溅射产额，以此统计羽流粒子对太阳翼表面作用的分布数据。具体模型细节将在第1.1和1.2节中介绍。

1.1 等离子体输运过程

等离子体羽流的输运过程，又称为广义双极扩散运动，主要包括带电粒子在电磁场中的受力运动和粒子间的扩散运动。对于霍尔推力器羽流而言，可以忽略自感磁场和外加磁场，只考虑空间电荷的电场作用。每一个网格内，每一个带电粒子在运动中所受总合外力都将遵循如下描述：

FTotal=FE+FE,AF+Fd

(1)

式中：FE为外加电场力；FE,AF为空间电荷所形成的电场力；Fd为浓度梯度力。对于空间电势，采用求解泊松公式的方法。

除带电粒子在电磁场中的迁移运动外，扩散运动也属于等离子体的双极扩散。扩散过程是一种对浓度梯度的响应过程，尤其在真空环境下，这种机制就必须要考虑。尽管PIC/DSMC在计算过程中，通过对粒子温度的热速度计算可以描述粒子，但根据已报道的计算结果来看[13]，这种描述存在一定的误差，考虑可能是适用于中性原子的热速度模型对于带电的离子来说，在求解输运过程时会产生兼容性的问题(带电粒子主要基于对力的求解，这与热速度的耦合在算法上会有兼容性问题)，为提高计算精度，这里采取一种经验性的修正。

需要说明的是，在后文的计算中，中性气体的速度求解依然应用热速度模型，而正离子的扩散运动采用基于浓度梯度力的计算思想(菲克定律)[14]：Xe+离子在等离子体环境中的扩散过程，微元空间某点A对另一点B的浓度扩散力Fd为：

(2)

式中：kd为扩散系数，根据本文计算结果，在10-36N·m4的量级与试验可以有较好的吻合趋势；Ni为离子浓度(即数密度)；l为两点间的距离。

综上，需要对2个参量进行节点分配计算：电荷和数密度。为此，引入单元粒子法。

1.1.1 单元粒子法(PIC)

在PIC模拟中，通常要用节点的统计参数来代表网格内的粒子状态，因此需要以某种原则，将网格内所有粒子的关注参数分配到节点上。一般采用权重分配，常用的处理方法是：对于二维问题，采用面积权重法；对于三维问题，采用体积权重法。以二维问题为例，电量为q的离子分配给网格节点i的电量为：

(3)

式中：Ai为各个部分面积，如图1所示。

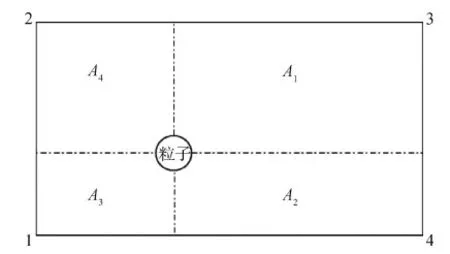
图1 物理参数在节点分配的方法Fig.1 Assignment strategy of the physical parameters to mesh node

可以利用节点上各项物理参数(如电荷、数密度)等求解相应的运动状态参数(电场力、浓度梯度力)。

1.1.2 直接蒙特卡洛法(DSMC)

本文只介绍所考虑到的碰撞类型：

1) Xe-Xe弹性碰撞，是一种自由程0.005～0.1 m内的碰撞，发生频率较高，不可忽略；

2) Xe-Xe+弹性碰撞，该碰撞的自由程在0.001 m左右，不可忽略；

3) Xe-Xe+CEX碰撞，该类型碰撞是影响羽流发散最为重要的碰撞，自由程在0.005 m左右，是羽流中最为重要碰撞类型。

3种类型碰撞的碰撞截面公式见表1。

表1 3种碰撞类型的碰撞截面

Table 1 Collision section equations of three types

碰撞类型碰撞截面Xe-Xe+弹性碰撞σelasticXe,Xe+ =6.42×10-16crXe-Xe+CEX碰撞σcexXe,Xe+ =(-23.10lncr+138.5)×0.8423×10-20Xe-Xe弹性碰撞σelasticXe,Xe =2.12×10-18c0.24r

需要说明的是，CEX碰撞截面公式中含有经验参数，本文根据已有推力器试验件进行了修正，所以该公式与先前文献不完全一致。

1.2 粒子与壁面的相互作用过程

等离子体羽流与太阳翼的相互作用包括电荷与溅射两方面，电荷方面主要是指翼板壁面所形成的鞘层电势；而溅射方面主要是指高能离子对太阳翼壁面所产生的溅射产额。前者影响入射离子的能量，后者影响透光率。

1.2.1 悬浮电极的鞘层电势模型

太阳翼壁面相对于霍尔推力器属于悬浮电极，因此，该鞘层模型属于悬浮电极下的电子鞘层模型，根据Langmuir-Child鞘层理论[15]，鞘层电势的计算过程如下。这里存在一个假设，电极所在位置的等离子体处于均匀分布假设：np=ni=ne(电子数密度接近离子数密度)。

离子通量密度为：

Γi=npci

(4)

式中：ci为离子入射速度；np为等离子体数密度。而电子通量密度为：

(5)

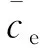
对于悬浮电极来说，电子通量与离子通量相等，有：

Γi=Γe

(6)

于是有：

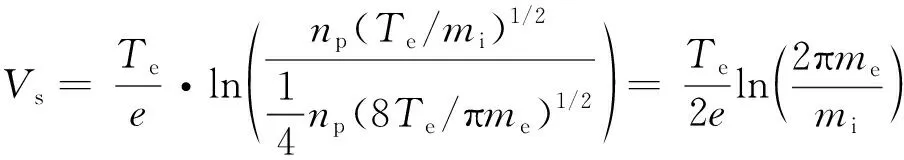
(7)

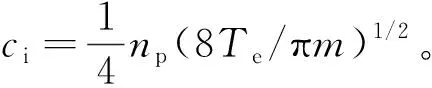
因此，Xe+离子入射能量为进入鞘层时的动能加上鞘层电势能，即

(8)

式中：vi为离子入射速度；Ei为离子撞击壁面的动能(该物理量可转为eV单位制)。

1.2.2 溅射产额计算

根据相关的溅射理论，只有当撞击壁面的粒子动能超过壁面材料的溅射阈值时，才会发生溅射。对于本文而言，太阳翼的壁面材料为二氧化硅，其溅射阈值与硅相近，取91eV。因此，对于入射动能超过91eV的Xe+离子：

1) 若入射角度为垂直于壁面时，溅射产额Y(0)为:

(9)

式中：P为与入射粒子种类相关的因子；sn(ε)为核阻止截面；se(ε)为电子阻止截面；ε为入射粒子当前的简并能量(无量纲)；Us为壁面材料的升华能；Eth为二氧化硅的溅射阈值,取91eV。该公式各项参数的具体取值可以参考文献[10]和文献[11]。

2)对于大多数的Xe+离子，入射角度都不是0°，但此时的溅射产额与Y(0)有关，那么对于入射角度为θ的Xe+离子而言，溅射产额Y(θ)为：

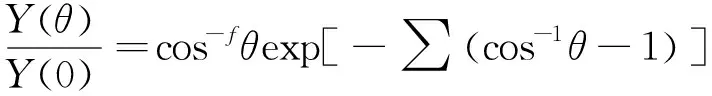
(10)

该公式中的各项参数取值依然可以参考文献[10-11]。

2 验证试验

本文所使用的计算模型分为两部分：1)等离子体流场输运模型(包含离子扩散机制)；2)等离子体对太阳翼的溅射模型。其中，模型1是加入了新物理机制，而模型2已在以往的研究中得到验证。因此，本文仅针对模型1进行试验验证以及相关参数修正。

在真空舱内开展羽流诊断试验，如图2所示。采用1.35 kW霍尔推力器作为试验和仿真中产生羽流的推力器，为对模型中经验参数kd的修正具有一定覆盖性，试验共选取了3组有代表性的工况：

1)工况1(标准工况)，放电电压300 V，放电电流4.5 A，总气体流率5.488 mg/s；

2)工况2(大推力工况)，放电电压280 V，放电电流4.82 A，总气体流率6.174 mg/s；

3)工况3(高比冲工况)，放电电压380 V，放电电流3.56 A，总气体流率3.724 mg/s。

以法拉第探针对距离推力器1 m半径内的10个角度位置进行电流密度的测量，具体见图2(b)。

各算法下的计算结果与试验结果的对比见图3。在没有修正离子扩散模型前，离子在轴向输运过程中只有受到碰撞才会向两侧运动，但在羽流远场中，浓度扩散作用与电场迁移作用相当，如果采用原有扩散模型会有很大的误差，所以图3的黑色曲线数据会偏离试验结果较多。

在引入离子扩散系数kd后，根据工况不同，该系数取值又会出现不同。这里给出了3种工况下最为吻合的3个kd取值，可以看出，从大推力到高比冲2种极限工况范围内，kd的浮动范围在1.24～1.29×10-36N·m4。由此，在下文的数值计算中，取kd=1.26×10-36N·m4。需要说明的是，由于菲克定律是基于流体模型，而粒子模型采用这种思想会有一定误差，所以扩散系数kd是一种经验参数，并不具备对所有工况的通用性。本文认为在10-36N·m4量级时会有较好的吻合结果，但其他学者在使用该模型前，依然要根据实际推力器及环境条件来修正该参数。在该修正下，3种工况所对应的平均误差可以在8.7%左右，可满足下文数值计算需要。

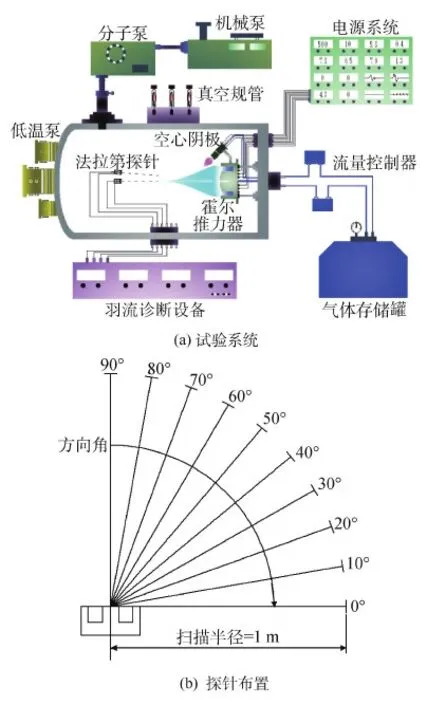
图2 验证试验的系统布置Fig.2 Systematic diagram of the rectification test

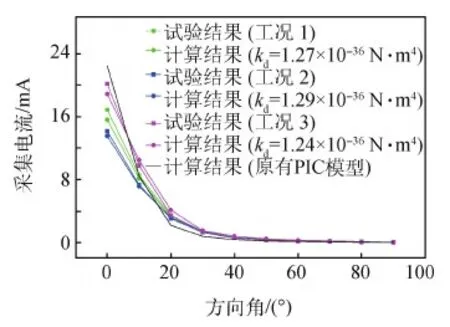
图3 各工况下试验与计算结果对比Fig.3 Comparisons of test and calculation results in each case

3 计算结果与讨论

针对卫星在轨工作情况，进行在多种推力器布置下的太阳翼溅射产额分布的数值计算，具体推力器的工作参数和布置方位见图4。

针对上述20组工况，进行霍尔推力器羽流的相关参数计算，羽流在稳态下的各物理参数分布结果见图5，该结果作为溅射计算的输入条件。溅射质量密度的分布计算结果见图6。

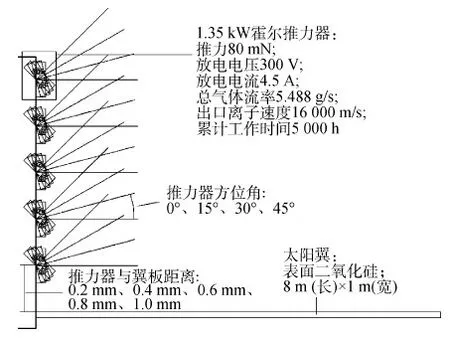
图4 推力器各布置工况和计算输入Fig.4 Layout cases and input conditions of the thruster

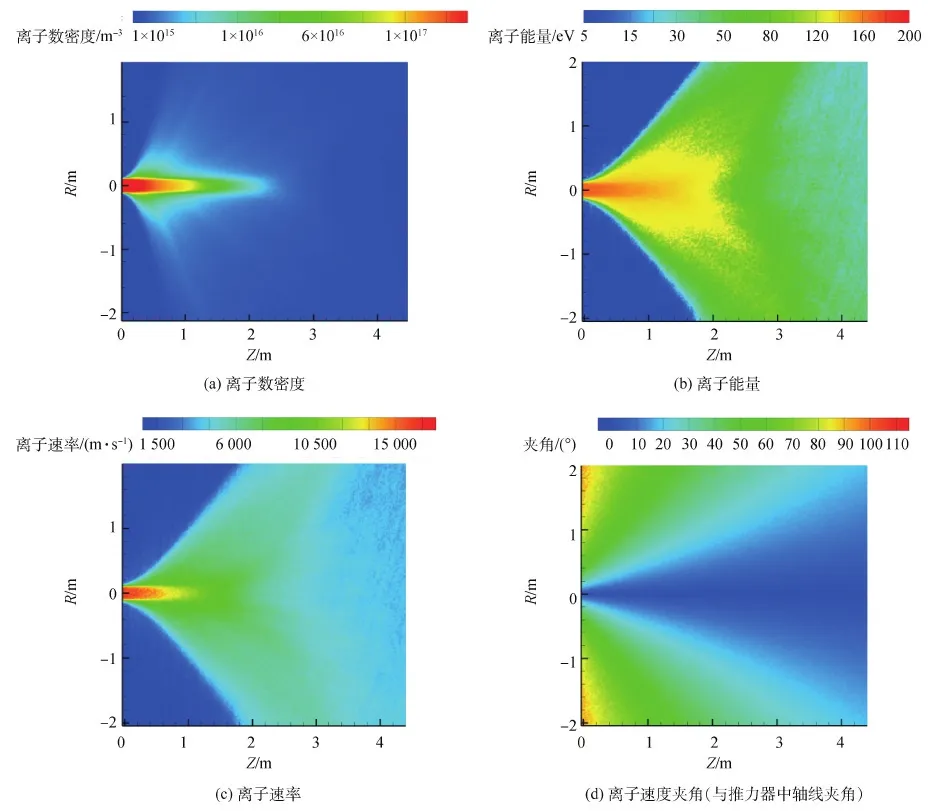
图5 羽流各物理参数分布云图Fig.5 Distribution contours of plume physical parameters

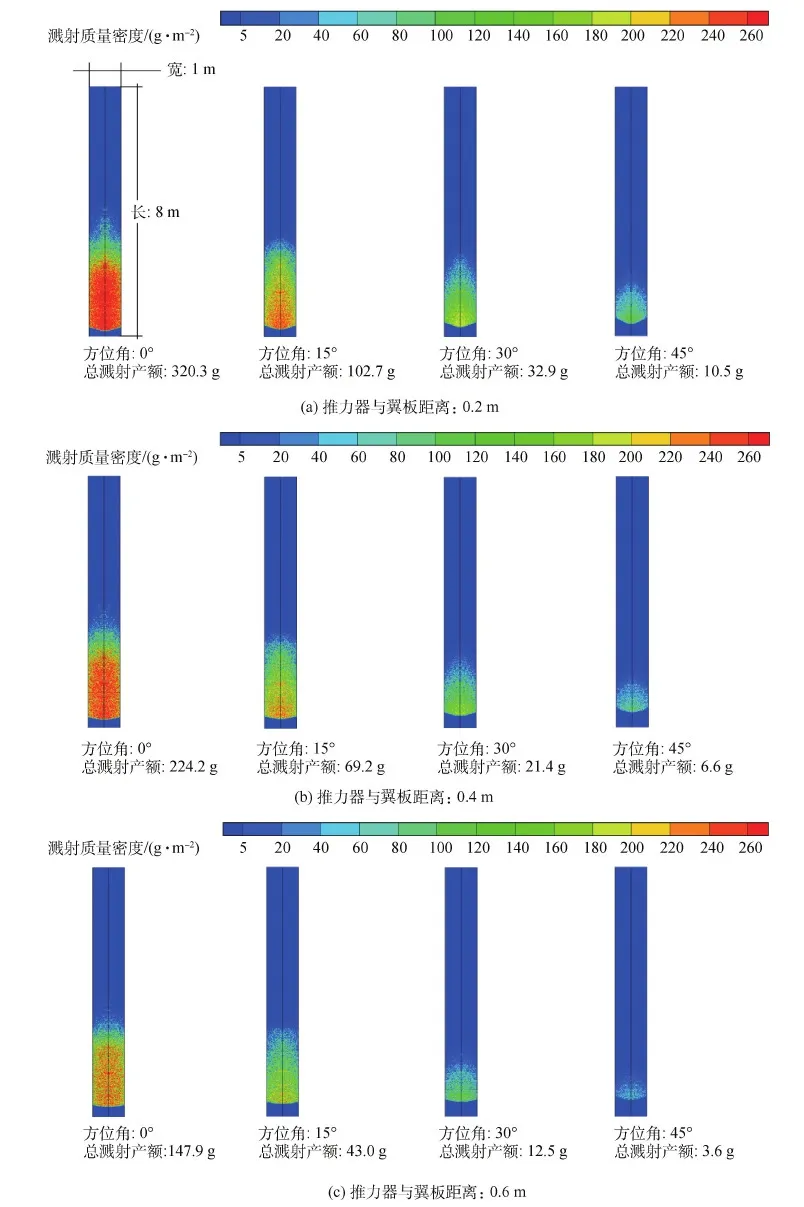
图6 各工况下的羽流对太阳翼的溅射产额密度分布(累计5 000 h)Fig.6 Sputtering yield density of the plume onto solar plane in each case (sum up to 5 000 h)

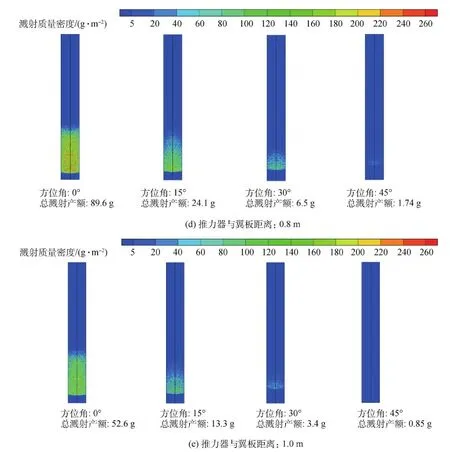
续图6Fig.6 Continued

根据图6，可以获得霍尔推力器羽流对太阳翼的3个主要规律：

1) 随着推力器与翼板距离的增加，溅射在整体分布和总量两方面都有降低的趋势，根据总溅射量进行曲线耦合，服从二次函数规律，见图7(a)；

2) 随着推力器方位角的增加，溅射在整体分布和总量两方面都有降低的趋势，根据总溅射量进行曲线耦合，服从指数函数规律，见图7(b)；

3) 太阳翼受到各工况下的溅射影响都具有一个溅射集中区域，并且这个集中区域会随着方位角和距离的增大而向外移动。

上述3种规律的产生主要与翼板壁面处的离子能量、数密度以及入射角度有关，随着距离和方位角的增加，由离子能量和数密度所带来的影响程度均有下降趋势，该机制主要导致规律1)和规律2)的产生。入射角度的影响机制比较复杂，在Xe+对SiO2的溅射产额随角度的变化曲线中，峰值点出现在65°～80°之间，角度太小或太大都会降低溅射量，于是该机制会导致距离、方位角发生变化时，溅射峰值区域发生漂移，主要对规律3)有较大影响。另外，由规律1)和规律2)揭示出：推力器方位角对溅射的影响程度要高于推力器与翼板的距离。

在获得羽流对翼板溅射分布规律的基础上，将进一步讨论该影响规律对透光率的影响情况。首先，将羽流对二氧化硅的溅射作用假设为一种玻璃磨砂处理。一般地，当玻璃的磨砂厚度在1～10 μm时，每提高磨砂深度1 μm，透光率降低约6%。假设没有经过溅射的玻璃透光率为92%，将玻璃表面的溅射质量分布推导出翼板入纸面方向微小矩形区域的溅射深度平均值，以溅射深度表示磨砂深度。通过对溅射深度的计算，可以计算所有工况下太阳翼玻璃表面的透光率变化的分布，见图8。图中20种工况的布置情况与图4一致，以太阳翼表面某位置的溅射深度计算出该位置的透光率，并且以白、黄、棕、黑4种颜色的线来表示透光率降低到初始值的百分比。

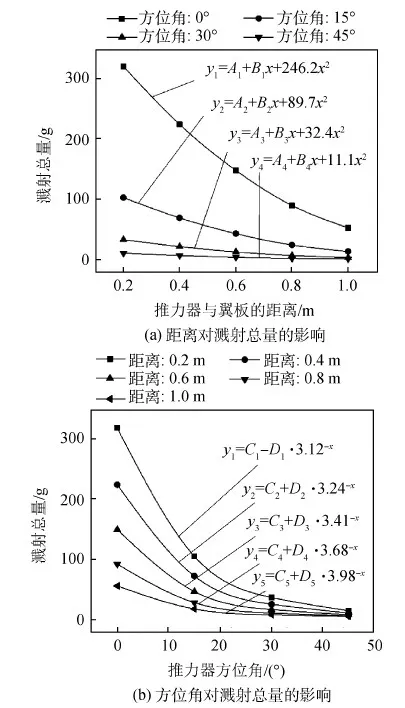
图7 溅射总量与距离、方位角的耦合曲线Fig.7 Fitting curves of total sputtering yield vs. installation angle and distance between thruster and panel

根据图8，对各工况下翼板透光率影响恶劣的区域只占太阳翼的一部分，那么对于整个太阳翼来说，平均透光率实际上并不会降低太多。本文对各个工况下的翼板平均透光率进行计算后，为了将影响程度高于5%的工况和其它工况区分开来，人为地在图8中给出一条参考曲线(红色虚线)。该曲线的意义为：只要太阳翼不穿过该曲线(方位角不小于0°)，则可认为平均透光率下降不会超过5%。需要说明的是，该曲线是一条由苛刻的仿真条件给出的上限预估边界，是一条保守边界，即可能存在穿过该曲线的翼板，其透光率不会下降5%，但是，不穿过该曲线的翼板透光率一定不会降低5%。接着，给出仿真所涉及到的所有苛刻条件设定：

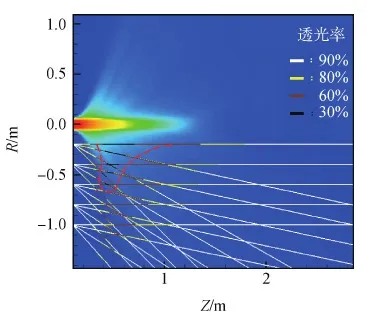
图8 太阳翼各处透光率分布(累计5 000 h)Fig.8 Distribution of the light transmittance on the solar panel (sum up to 5 000 h)

1) 翼板壁面等离子体参数预估苛刻：由验证试验与计算对比可见(图3)，只有在80°～90°时，试验值才高于计算值，其它0°～70°时均是计算值高于试验值，而太阳翼位于推力器0.2 m以外、0°角以上，其工况大部分位于探针所测的0°～70°的区域，所计算得到的翼板壁面等离子体数量和能量都会高于实际情况。

2) 鞘层无碰撞假设预估苛刻：鞘层模型采用的是离子无碰撞假设，意味着只要能够进入鞘层，离子均会以无能量损失的状态撞击翼板壁面。

3) 溅射作用的等效预估苛刻：玻璃磨砂作用要比溅射作用更为严重，因为磨砂是利用硬度较高的金刚砂等物质进行表面打磨以及用相关化学物质进行表面残渣清理，以造成玻璃的不透明，这种处理方式明显针对性较强，阻光机制更为有效，所以以溅射机制等效为磨砂机制是一种苛刻条件假设。