磁拓扑结构对环型离子推力器放电性能的影响

2018-11-19，，，，，，

中国空间科学技术 2018年5期

，，，，，，

兰州空间技术物理研究所真空低温技术与物理重点实验室，兰州 730000

离子推力器作为一种先进空间技术，其先进性突出体现在高比冲、高效率、长寿命、推力和比冲调节容易实现等方面。航天器采用离子推力器可显著增加卫星有效载荷质量、延长卫星工作寿命、降低卫星发射成本等[1]。但受限于栅极组件引出能力，目前工程上实现的离子推力器最高功率仅为50 kW，极大限制了其空间应用范围。

2012年美国NASA格林研究中心首次提出环型离子推力器[2-3]概念，不同于传统离子推力器，该推力器放电通道和栅极组件呈环状结构，通道面积的增加可有效增大推力器放电电流、提高等离子体分布均匀性，而环状栅极可极大减小传统栅极几何尺寸，解决大尺寸栅极热稳定性问题，同时该栅极还能减小束流发散角。国外已研制了环型离子推力器原理样机，并完成了推力器点火试验测试和等离子体特征参数测量。国内兰州空间技术物理研究所于2015年首次开展5 kW级环型离子推力器原理样机研制，其推力器性能参数为：推力150 mN；比冲5 000 s。作为一种全新结构离子推力器产品，到目前为止还未形成一套其完整的推力器设计准则。为了节约产品研制成本，加快研制进度，兰州空间技术物理研究所在环型离子推力器物理方案设计中首次采用数值计算方法。

对离子推力器而言，通常提高放电效率的方法有两种[4]：1)优化磁场分布以尽可能地约束电子运动，延长电子在放电室内停留时间，提高电子和中性原子之间碰撞概率，最大化电离率；2)缩小阳极对电子吸收面积来减小放电损耗以提高放电效率。后者虽然阳极面积减小能更加有效约束电子运动行为，但它却仅仅改变了相对阳极势的等离子体势而并没有改变由于离化或激发所产生的能量损耗率。值得注意的是，阳极面积不能过小，因为当阳极面积非常小时，等离子体势相对阳极势为负值，此时磁尖端处的阳极面积不足以收集所有放电电流，致使放电被打断或变得不稳定。因此，为了保证放电稳定必须要保证阳极面积和等离子体势不能超过其最小值。对一种特定结构下的离子推力器，通常通过优化放电通道内的磁场分布来提高放电效率。为得到5 kW级环型离子推力器最佳磁拓扑结构，选取传统型离子推力器环尖场[4]和已成功应用于高效率多阶段等离子体推力器(High-efficiency multistage plasma thruster)的多极场[5-6]作为环型离子推力器磁场的设计输入条件，利用仿真计算手段分析两种不同磁结构下的等离子体运动特性和放电特性。

国外已针对离子推力器开展过磁位型及磁场强度优化研究。Matossian等人建立了离子推力器放电室理论分析模型，研究磁感应强度对放电损耗的影响[7]。Sandonato等人利用该模型研究了磁感应强度对原初电子运动特性的影响[8-9]。Ogunjobi等人采用MAXWELL 2D和PRIMA数值计算方法分析了不同磁位型及磁感应强度下的原初电子受约束程度和运动特性[10-13]。Wirz等人建立了二维数值仿真模型，采用混合模拟方法研究了环尖场结构下不同磁位型对等离子体分布特性、放电室性能和束流分布的影响[12-14]。Menart等人试验测量了3环、4环磁结构下的离子饱和电流，分析了两种磁结构对推力器性能的影响[15]。

以上研究均只考虑了环尖场结构的下离子推力器放电性能，并未考虑磁位型及磁感应强度对放电稳定性的影响。本文针对5kW级环型离子推力器，创新性地提出多极场磁构型，通过建立环型放电通道数值计算模型，采用Particle-in-Cell(PIC)-Monte Carlo Collision(MCC)数值计算方法模拟环尖场和多极场两种磁构型下的气体放电过程，分析其放电特性和放电稳定性，确定最佳磁结构，完成推力器磁体组件设计，并开展试验验证。

1 数值模型

1.1 仿真区域

仿真区域示意如图1所示。

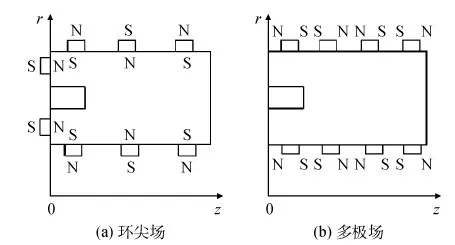
图1 磁场构型Fig.1 The structure of the magnetic field

计算区域具参数如图2所示。

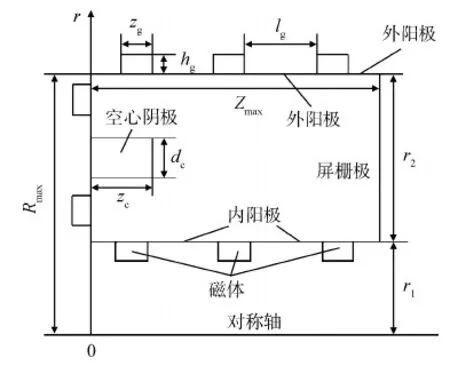
图2 计算区域示意Fig.2 Schematic diagram of the calculation area

考虑到环型离子推力器环型放电通道的轴对称性，选取其一半作为仿真区域，其中：z为轴向位置，r为径向位置，Zmax和Rmax分别为计算区域轴向、径向最大值，r1和r2分别为推力器内、外环半径，zc、dc分别为空心阴极长度和直径，zg、hg分别为磁体宽度和高度，lg为两磁体之间间距。计算区域左下角定义为坐标原点；左边界、上边界和下边界均为阳极边界，其电势为阳极电压Va；右边界为屏栅极表面，其电势为屏栅电压Vs；与等离子体接触的空心阴极表面假设为一等势体，其电势为触持极电压Vc。

将计算区域划分成N×N个正交网格，为保证计算结果的有效性和准确性，每个网格尺寸必须小于德拜长度：

(1)

计算时间步长小于等离子体振荡频率的倒数。等离子体振荡频率表达式为：

(2)

式中：ε0为真空介电常数；kB为玻尔兹曼常数；Te为电子温度；ne为电子密度；me为电子质量。放电通道内质量较小的电子在电场加速作用下速度快速增加，而质量大的离子几乎不受磁场的约束，在电场作用下沿磁力线做慢加速运动。要在同一个计算区域同时模拟电子和离子，这在技术上是非常大的挑战。在此，本文采用增大真空介电常数[13]和减小离子质量[13]相结合的方法，通过改变离子德拜长度和等离子体振荡频率，人为的增大网格大小、减小离子时间步长，从而实现在同一时空下对电子和离子运动行为的同时跟踪，并实现计算的可收敛性。本文所取的空间步长为1.0×10-3m和9.0×10-9s。

1.2 PIC-MCC模型

针对低温气体放电过程，本文采用常用于低温等离子体数值模拟的一种方法PIC来求解电磁场分布和描述带电粒子运动，粒子间碰撞则采用MCC数值计算方法，本模型中的碰撞主要考虑电子和中性原子之间的弹性、激发和电离碰撞，电子和一价氙离子之间的电离和再结合反应。

PIC模型中，二维轴对称坐标系下的麦克斯韦方程可简化为：

(3)

式中：Aθ为磁势；μ为磁导率；Hcz、Hcr分别为轴向、径向矫顽力。由于磁场分布的特殊性，使其在计算时求解区域将远远大于图2所示计算区域。

电势分布由泊松方程求解得到：

(4)

式中：e为电子电量；ε0为真空介电常数；ni和ne分别所示为离子、电子密度。

式(4)右端为0时，泊松方程退化为拉普拉斯方程，此时求解得到的电势为静电势φstatic。当放电室内存在等离子体时，式(2)计算得到的电势为运动等离子体产生的自洽电势φdynamic，其值相比几千伏的静电势来说很小，因此，可将放电室内静电势和自洽电势分别进行求解。放电室内总电势表达式为：

φ=φstatic+φdynamic

(5)

进一步计算出电场：

E=-φ

(6)

带电粒子运动方程满足牛顿第二定律：

(7)

式中：m为带电粒子质量；x、v分别为粒子所在位置和速度；E和B分别为粒子所在位置处的电场强度和磁感应强度。

1.3 初始条件

每个时间步长空心阴极向计算区域内发射一定量原初电子，同时在计算区域右边界有一定数量离子和中性原子离开，具体离开的个数与屏栅极离子、原子透明度有关。每个时间步长，当右边界离开的离子数与阴极发射原初电子个数和返回阴极被其所吸收的离子数之和等于阳极吸收电子数时，认为系统气体放电达到平衡。

每个时间步长阴极发射的原初电子个数与空心阴极发射电流Ie有关：

(8)

式中：V为空心阴极体积。

本模型中初始时刻进入计算区域的原初电子位置采用直接抽样方法[16]得到。

原初电子轴向、径向位置分别表示为：

本以为我丢给沙莉的这块难啃的“硬骨头”会成为她手上的烫手山芋，谁知道，沙莉竟轻松地将此事处理得滴水不漏。最令我悔之晚矣的是，半月之后，那位投诉的李先生，被沙莉的真诚打动，竟向沙莉介绍了一位大客户，在李先生的帮助下，沙莉顺利地签订了最难销售的一批货。

(9)

式中：R1为0～1之间的随机数。

原初电子初始速度服从麦克斯韦正态分布，其表达式为：

(10)

式中：kb为玻尔兹曼常数，T、m分别为原初电子温度和质量，vi为原初电子速度。

原初电子在轴向、径向和方位角方向的速度大小分别为：

(11)

式中：vth为原初电子总速度大小;ψ=2πR1为z、r平面内速度矢量与z轴方向的夹角;cosφ=1-R2为速度矢量与方位角方向的夹角;R1、R2均为随机数。

1.4 边界条件

本模型中利用PIC方法跟踪的带电粒子包括原初电子、二次电子、一价氙离子和二价氙离子。对电子而言，计算区域阳极边界为吸收边界，屏栅极边界为反射边界。一价离子和二价离子在阳极处的边界条件不同，二价离子阳极边界为吸收边界，一价离子则和阳极附近电子发生再结合反应变为中性原子或发生二次电离反应。是否发生二次电离反应可根据阳极壁面的二次电子发射系数来确定。屏栅极边界处大部分离子将通过屏栅极孔从计算区域中泄漏出去，少量离子直接轰击到屏栅极表面被其吸收，仿真过程中，计算机随机产生一个随机数，当该随机数小于屏栅极离子透明度时，表示离子通过屏栅极孔进入栅极组件，反之则认为被吸收。泄露出去或被吸收的离子计算机均做删除处理。

2 计算结果分析

假定推力器几何结构尺寸、工作电气参数、磁体个数及磁体几何尺寸完全相同，具体参数值见表1、表2所示。仿真计算收敛条件为电场变化小于0.10%。

表1 几何结构尺寸

表2 工作电气参数

表2中Ib为推力器能够引出的最大束流。

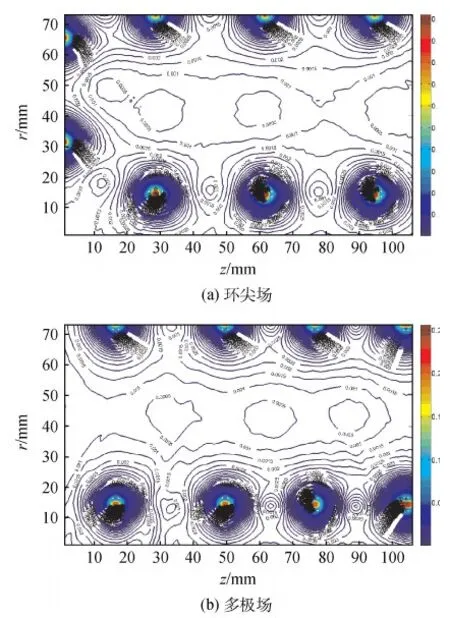
图3 磁场分布Fig.3 Magnetic field

计算结果显示，两种磁构型下，放电通道内绝大部分区域磁场分布趋势基本一致，尤其在上下阳极边界处除了由于磁体位置不同引起的磁力线分布有差异外，其分布趋势几乎完全相同。放电通道中心区域无磁场区大小相当。最靠近通道中心的闭合磁等势线值均为10-3T。磁场分布区别较大的区域位于计算区域左边界、空心阴极附近和屏栅极边界。左边界处，环尖场情况相比多极场其磁力线分布更密集，除空心阴极位置处外，磁力线几乎布满整个左边界，磁感应强度变化范围约为6×10-4～2×10-2T。而多极场情况下左边界仅有一小部分区域存在磁力线，且磁感应强度变化范围仅为0～6×10-4T。空心阴极附近，环尖场情况下磁力线相较多极场情况分布更密集，相应磁感应强度较大。屏栅极边界处，环尖场情况下无磁场区或磁感应强度较小的分布区域较多极场情况稍大。

图4所示为放电通道轴对称处磁感应强度随轴向坐标的变化曲线及屏栅极附近磁感应强度随径向坐标的变化曲线。

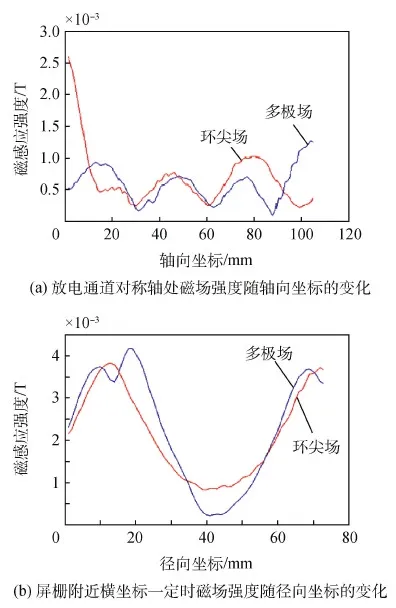
图4 磁场强度随坐标的变化关系Fig.4 Magnetic field strength

图4仿真计算结果进一步印证了图3所示仿真结果。图4(a)计算结果显示，在放电通道中心轴向方向，多极场情况下磁感应强度变化幅度很小，变化趋势基本一致，仅在屏栅极附近磁感应强度突然增大，但增大幅度仅为6.2×10-4T。根据磁感应强度与电子原子之间碰撞概率之间的关系[4]可知，此时对应碰撞概率仅为0.047，该碰撞概率几乎不会影响放电效率。环尖场情况下，从计算区域左边界到空心阴极出口距离3 mm范围内，磁感应强度发生突降，由原来的2.58×10-4T降至8.9×10-4T。在其他位置除屏栅极边界处和多极场情况变化趋势相同。图4(b)计算结果显示，在屏栅极附近两种磁构型下磁感应强度随径向位置的变化趋势基本一致。

图5所示为两种磁构型下气体放电过程中被阳极表面吸收的原初电子个数随时间步长的变化曲线。

图5计算结果显示，随气体放电的进行被阳极吸收的原初电子个数逐渐增大。放电初期，环尖场情况下被吸收的原初电子个数远小于多极场情况，之后这种差异逐渐减小，在气体放电达到稳态时该差异达到最小。对比每个步长进入的原初电子个数和图5统计结果可知，多极场情况下放电初期原初电子损耗率高达86.96%，环尖场情况下的损耗率为43.12%。分析认为这是因为放电初期空心阴极发射的能量较低原初电子进入计算区域后沿着磁力线向阳极壁面做加速螺旋运动过程中，在环尖场阴极附近和阳极表面磁场的作用下受到磁镜效应影响做往复运动，而多极场情况由于左边界磁场分布稀疏、磁场强度较小，导致原初电子直接吸收。

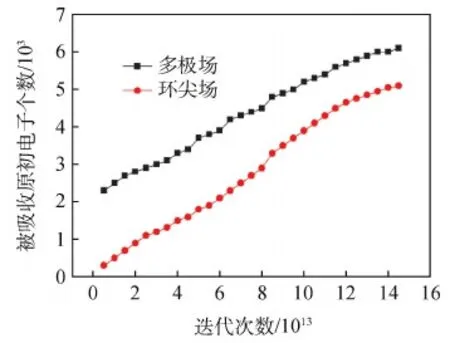
图5 被阳极表面吸收的原初电子个数Fig.5 Numbers of primary electrons absorbed by the anode surface

图6所示分别为环尖场和多极场结构下，气体放电达到稳定时上阳极边界处鞘层电势降随轴向坐标的变化曲线。

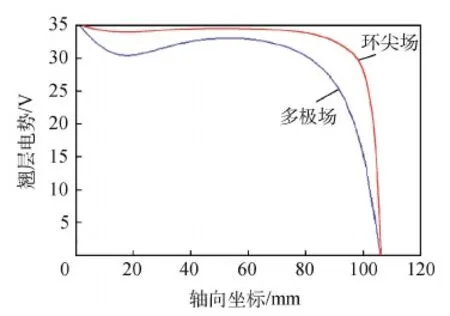
图6 鞘层电势随轴向坐标的变化Fig.6 The variation of the sheath potential

结果显示，两种磁构型下鞘层电势降随轴向坐标的变化趋势相同，且其值相差不大。在整个计算区域内两种情况下的鞘层电势降均为正值，这就意味着阳极壁面双极性扩散运动形成的鞘层可以加速离子、而减小电子速度，以保证鞘层内的等离子体准中性特性，阳极壁面能够正常吸收电子以维持稳定放电[13]。相比多极场情况，环尖场情况下运动等离子体产生的鞘层电势降稍大，分析认为放电通道内的等离子体鞘层电势降与推力器几何结构参数、工作电气参数等有关[4]，当其他参数一定时阳极壁吸收电子个数越少即阳极电流越小，鞘层电势降越大。计算区域最右侧鞘层电势降从几十伏下降至零伏，这是在靠近屏栅区域的鞘层电势变化趋势，进一步印证了离子推力器放电通道内鞘层电势大于壁面电势。

图7所示为推力器气体放电达到稳定时放电通道内部氙离子数密度分布。离子数密度单位为m-3。

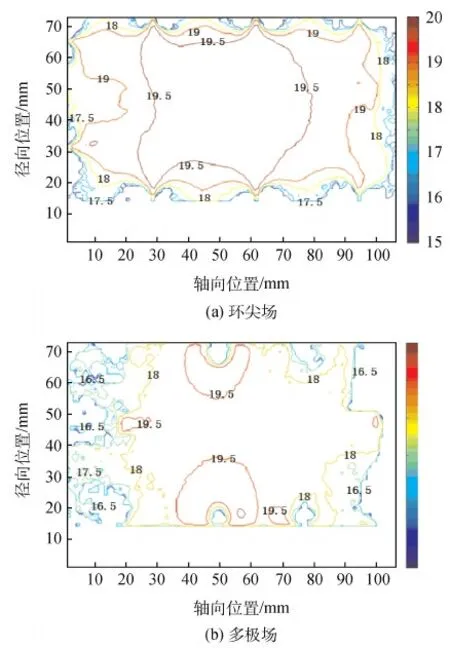
图7 氙离子数密度分布Fig.7 Number density distribution of the Xenon ions

根据式(8)，每个时间步长进入放电通道内的原初电子个数2 875及图5统计得到的结果，可知放电初期多极场和环尖场工况下的电子损耗率分别为2 500和1 240。因此，多极场情况下放电初期原初电子损耗率高达86.96%，环尖场情况下的损耗率为43.12%。

结果显示，在相同几何结构尺寸、工作电气参数、磁体几何尺寸及中性原子分布情况下，环尖场结构放电通道内部氙离子布满整个空间且分布很均匀，尤其在屏栅极附近氙离子分布非常均匀，极大提高了推力器放电效率和工作寿命[4]。

以上仿真分析认为环尖场是最适用于5 kW环型离子推力器的磁场构型。

3 试验验证

为了验证计算结果的正确性，对5 kW级环型离子推力器原理样机开展了点火试验测试和性能试验测试。该试验在兰州空间技术物理研究所TS-6平台上进行，根据推力器的机械接口及气电接口对推力器和试验测试设备进行了对接。试验连接以及测试细则见参考文献[20]。试验中分别测试触持极电压及电流、阳极电压及电流、屏栅极电流、阳极工质流率等。

图8所示为5 kW级环型离子推力器原理样机示意图、点火照片。

图8 试验测试结果Fig.8 Experimental results

结果显示推力器能正常工作，验证了磁场选择的正确性。为了更进一步验证仿真计算结果的正确性，试验测量了推力器工作参数，计算得到了放电性能曲线，如图9所示。

该结果为在原推力器几何结构及磁体结构基础上，不断改变磁铁电流后试验测量到的结果。试验结果显示，随着通道内工质利用率的增大，放电损耗逐渐增大，当工质利用率增大到某一点时，放电损耗突然急剧增大，这与传统型离子推力器性能变化曲线完全相同[4]。曲线最佳拐点为，工质利用率为89%，对应放电损耗为275 W/A。该值高于传统离子推力器放电损耗，这是环型离子推力器阳极面积增大提高了电子损耗率所致。

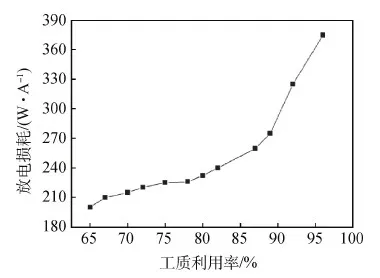
图9 性能曲线Fig.9 Performance curve

图10所示为试验测量到的放电损耗与仿真计算得到的结果对比示意图。

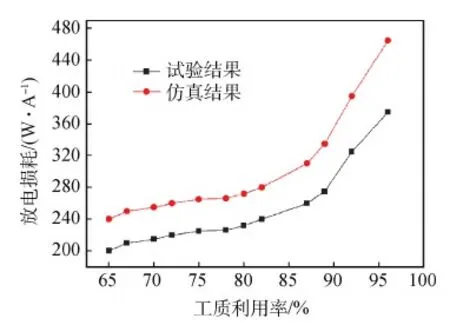
图10 仿真结果与试验结果对比Fig.10 Comparison of the simulation and experimental results

从图中可以看出，两者具有相同的变化趋势。进一步对比显示，数值计算结果均大于试验测试值。针对该差异，分析认为，本文建立的仿真计算模型在处理阳极表面二次电子运动时假设电子能量较低，不会与附近氙离子发生再结合反应或二次离化反应，二次电子在碰到阳极边界后会直接被阳极吸收，导致仿真计算结果中通道得到的放电电流较实际增大，在放电电压和引出束流不变的情况下，放电电流越大，放电损耗越高，因此计算结果整体偏高。同时忽略了放电通道内原子与原子之间的碰撞及原子分布特性对气体放电过程的影响。针对以上因素，后续将根据试验测试结果进一步完善仿真计算模型。