偏心受压构件大小偏心不确定性的研究
2018-11-15肖光宏汤名豪
肖光宏,汤名豪,谢 鑫
(重庆交通大学 土木工程学院,重庆 400074)
0 引 言
钢筋混凝土矩形偏心受压构件是工程中常用的构件之一,对偏心受压构件的计算是设计时的重要环节。由于小偏心受压构件的计算需要求解一元三次方程,可能会导致在偏心受压构件判别时产生分歧,因此目前对偏心受压构件的研究主要集中在小偏心受压上。祝磊等[1]理论分析得出,在配筋率以及混凝和钢筋材料一定的情况下,钢筋混凝土柱将不会出现全截面受压的情况,小偏心受压时的相对受压区高度ξ总是满足ξb<ξ 笔者对现行规范JTG D 62—2012《公路钢筋混凝土及预应力混凝土桥涵设计规范》(以下简称《规范》)中偏心受压构件判别的方法进行了研究,首先,理论分析了大小偏心受压公式中解(即受压区高度)的分布情况,研究大小偏心判别的不确定性现象;然后,用算例验证了受拉钢筋应力的不连续对承载力的影响,研究得到了偏心受压公式中解的分布情况。研究结果表明:一元三次方程在(0,+∞)上只存在唯一解,不会发生不确定性现象;在不同的偏心假设下,承载力在临界偏心距处均存在误差,且误差与偏心假设和材料强度有关。 《规范》对不使用预应力钢筋的矩形截面偏心受压构件抗压承载力的规定如图1及式(1)~式(8): (1) (2) (3) (4) 图1 矩形截面偏心受压构件正截面抗压承载力计算Fig. 1 Calculating the bearing capacity of eccentric compression member with rectangle section 求得ξ=x/h0,当ξ>ξb时,为小偏心构件;当ξ≤ξb时,为大偏心构件[6-7]。 式(1)中,受拉钢筋的应力σs按式(5)取值: (5) 先假设大偏心[8-10],再按式(6)进行试算得到x,然后求ξ: (6) 1)当ξ≤ξb时,即为大偏心构件; 2)当ξ>ξb时,应按照小偏心构件重新计算,联立式(5)、式(6),得到一个关于x的一元三次方程 Ax3+Bx2+Cx+D=0 (7) 求解方程(7),即可得到x及相应的ξ。承载力按式(8)计算: (8) 当钢筋混凝土强度不同时,发现临界状态下(即ξ=ξb),式(5)中σs值和fsd值不同。临界状态下σs值的分布如表1。 表1 临界状态下 s值Table 1 Value of s under critical condition MPa 表1 临界状态下 s值Table 1 Value of s under critical condition MPa 钢筋种类fsd/MPa混凝土强度等级≤C50C55C60C65HPB235195201.194216.125201.600216.698HRB335280282.857300.926288.444302.885HRB400330336.226356.863338.824360.000 表1显示,在临界状态ξ=ξb下,σs值始终大于fsd值,说明σs是一个关于x的不连续函数。因此,在临界状态附近,x的求解将会受到影响。 在临界状态附近,先通过大偏心公式求解到x>ξbh0,判断构件为小偏心,再代入小偏心公式进行重算,可能会出现x≤ξbh0的情况,使其再判断构件为大偏心,导致判断结果不确定性(图2),从而算法陷入死循环。 图2 不确定性现象Fig. 2 The phenomenon of nondeterminacy 笔者分别对①先假设为大偏心,②先假设为小偏心这2种情况,由式(6)、式(7)解得x的分布进行分析,来研究不确定性现象。同时对小偏心公式(7)进行论证,确定解x在(0,+∞)上的分布情况。 2.1.1 大偏心公式的试算 假设构件大偏心受压,首先根据式(6)计算出x,若x值在(0,ξbh0]之间(图3中的区间1),则假设成立,此时x值的分布情况如图3;若x值在区间(ξbh0,+∞)上,则需要按照式(7)重新计算。 图3 大偏心公式的解x的分布情况Fig. 3 Distribution of x solved by formula of large eccentricity 2.1.2 小偏心公式解的唯一性研究 由于式(7)为一元三次方程,在(0,+∞)上可能存在多解,因此在重算之前,需研究式(7)的解x在(0,+∞)上的唯一性。 对式(7)作相应的变换,得出函数式(9)~式(11): (9) (10) f(x)=f1(x)-f2(x) (11) 1)f1(x)的对称轴在y轴右侧时,即h/2-e0>0,对函数f(x)求导,得: (12) 式中:x+es-h0=x-(h/2 -e0)。 当x≥h/2-e0时,f′(x)>0成立;当x 2)f1(x)的对称轴在y轴左侧时,即h/2-e0<0,有f1(x)在(0,+∞)上单调递增,f2(x)在(0,+∞)上单调递减,则f(x)在(0,+∞)上单调递增。 综上,函数f(x)在(0,+∞)上单调递增,因此式(7)的解x在(0,+∞)上具有唯一性。 2.1.3 小偏心公式的重算 临界状态下,ξ=ξb,按照式(7)重算,解得的x有最小值,记为xmin。式(7)的解x位于图4的区间2内。 图4 小偏心公式的解x的分布情况 临界状态下,ξ=ξb,若式(11)中σs=fsd,则xmin=ξbh0,f(ξbh0)=0。而实际上,σs>fsd,所以xmin≠ξbh0,且f(xmin)=0,因式(11)中σs的系数为负数,故f(ξbh0) < 0。 由于函数f(x)在(0,+∞)上单调递增,则xmin>ξbh0,因此,在ξbh0和xmin之间存在一段如图5的空白区间。 图5 空白区间的分布情况 图5是先假设为大偏心的情况下,x的总体分布情况。图中空白区间说明式(7)解得的x值偏大,其原因在于σs的不连续性。所以,先假设为大偏心时,不会发生不确定性现象。 先假设为小偏心的情况下,由2.1.3可知,临界状态下,ξ=ξb,式(7)求解出的x值偏大。 当式(7)解得的x=ξbh0时,设x真实值为(ξbh0-Δ)。若x真实值位于(ξbh0-Δ,ξbh0)上,式(7)解得的x位于 (ξbh0,xmin)上,这时不会使用式(6)进行重算。将区间(ξbh0-Δ,ξbh0)定义为误判区间,若x真实值位于此区间内,构件将会被误判为小偏心受压构件,如图6。 图6 x真实值与公式解得的x值Fig. 6 Real x and the x solved by formula 由图6可知,先假设为小偏心时,将会发生以下3种情况: 1)若x真实值位于区间3中,则会被式(7)解到区间4′中,此时构件为小偏心受压构件。 2)若x真实值位于误判区间2中,则会被式(7)解到区间3′中,解得x>ξbh0,此时大偏心受压构件被误判为小偏心受压构件,发生误判现象。 3)若x真实值位于区间1中,则式(7)解得x<ξbh0-Δ,此时需要根据式(6)进行重算,最终将会被解到区间1′中,该构件仍为大偏心受压构件。 由于《规范》规定受拉钢筋应力σs是不连续的,因此区间2′是解不到的一段空白区间,所以,先假设为小偏心的情况下,x的总体分布情况如图7,此时不会发生不确定性现象。 图7 x的总体分布情况 受压区高度x和承载力Nu均为关于偏心距e0的函数。先假设为大偏心时,通过改变e0,利用式(6)求出x,再用式(8)求得承载力Nu。 图8 先假设为大偏心时计算承载力流程Fig. 8 Flow chart for bearing capacity under the large eccentricity hypothesis 图9 2种偏心假设下承载力Nu随偏心距e0的变化Fig. 9 Nu changing with e0 under two types of eccentricity hypotheses 1)在C30+HRB335组合下,临界偏心距处为一个跳跃间断点,这是受拉钢筋应力σs不连续造成的。 2)先假设为大偏心和先假设为小偏心2种情况下,在临界偏心距处承载力Nu的误差,C30+HRB335、C50+HRB335、C30+HRB400这3种组合分别为665N和2 066N、1 192N和2 796N、1 172N和3 780N。 3)对同一构件而言,在同一材料强度下,若先假设为大偏心,承载力Nu的误差值要小于先假设为小偏心的情况。相同的偏心假设下,随着材料强度的增强,误差值也随之增大。 1)通过分析论证,大小偏心公式求解出的受压区高度x具有唯一性,不会发生不确定性现象。 2)小偏心公式的一元三次方程的解x,在(0,+∞)中只存在唯一解。 3)由于受拉钢筋的应力σs是不连续的函数,先假设为大偏心时,会存在一个空白区间,先假设为小偏心时,会存在一个误判区间和一个空白区间,但是由于误差范围较小,因此小偏心受压公式在实际工程应用中是可行的。 4)针对同一偏心受压构件,在不同的偏心假设下,承载力Nu在临界偏心距处均存在误差,且先假设为大偏心时的误差小于先假设为小偏心时的误差,误差与材料强度呈正相关。1 问题的提出——不确定性现象
1.1 偏心受压构件的求解
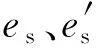
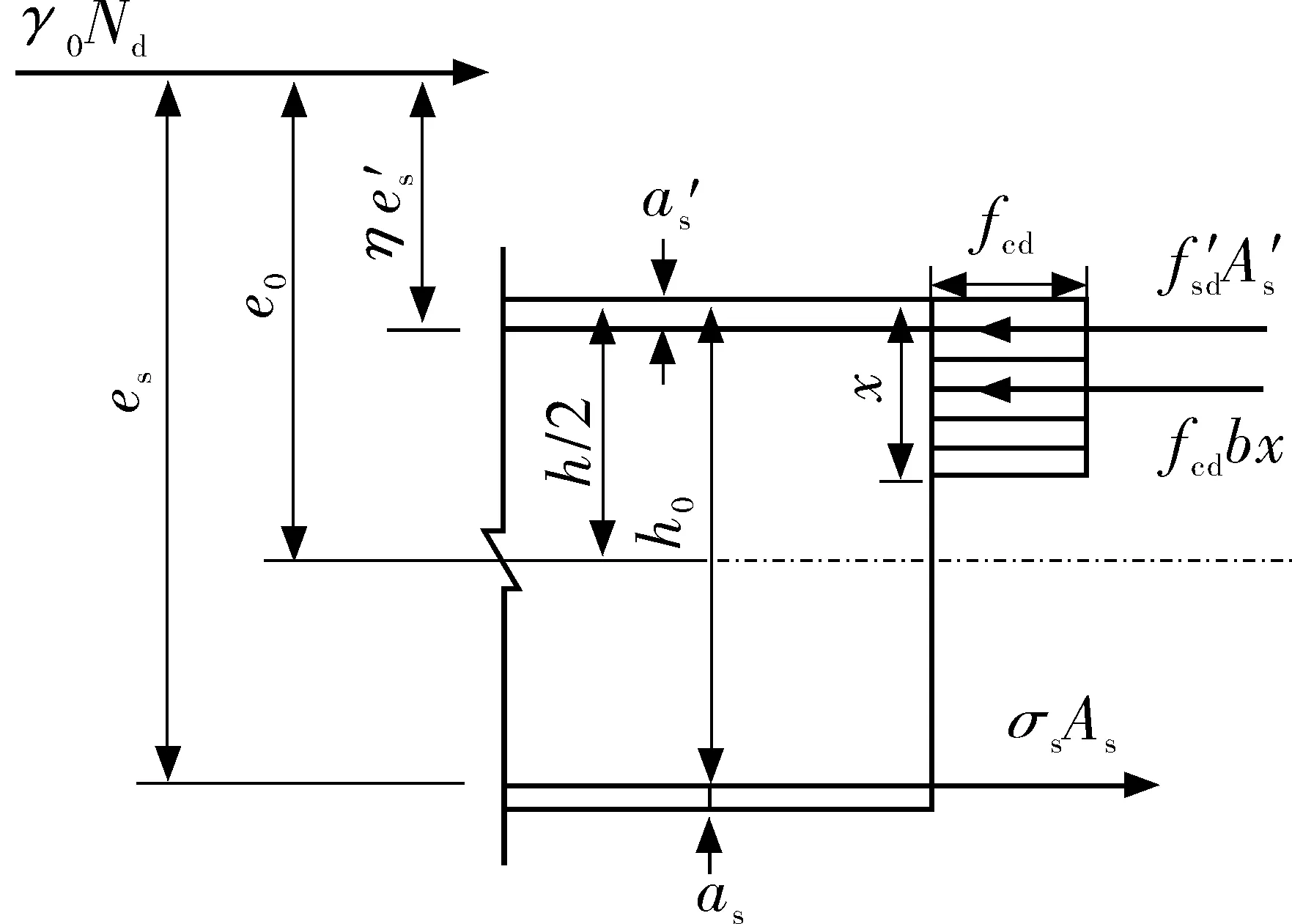
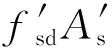
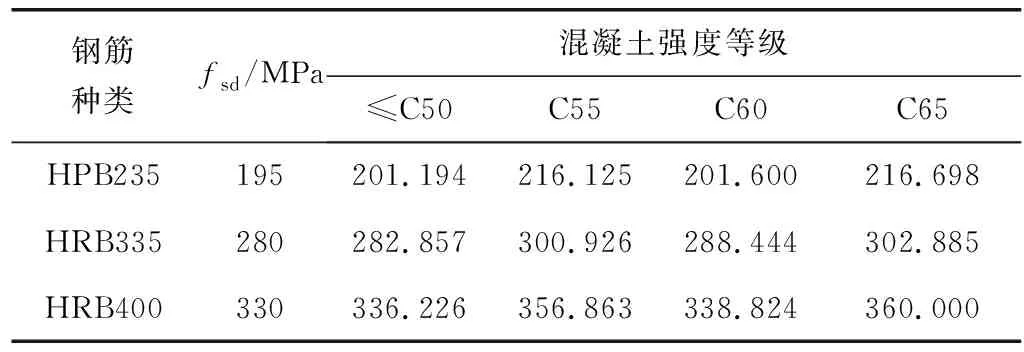
1.2 不确定性现象
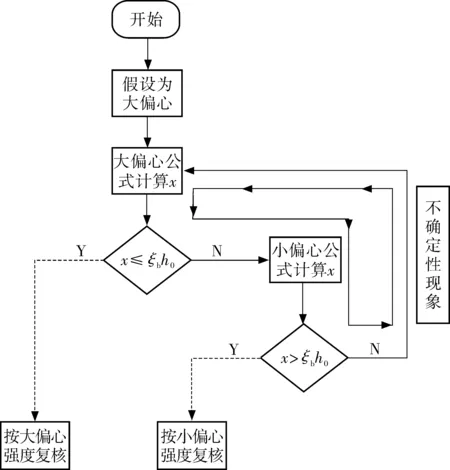
2 理论分析——受压区高度
2.1 先假设为大偏心

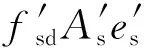
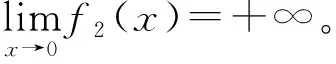
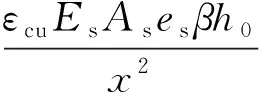

Fig. 4 Distribution of x solved by formula of small eccentricity
Fig. 5 Distribution of blank interval2.2 先假设为小偏心
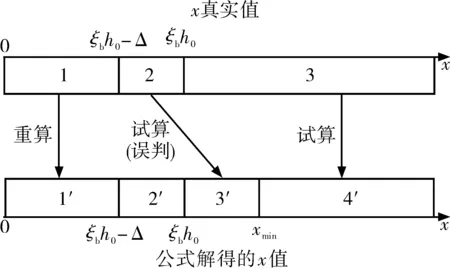
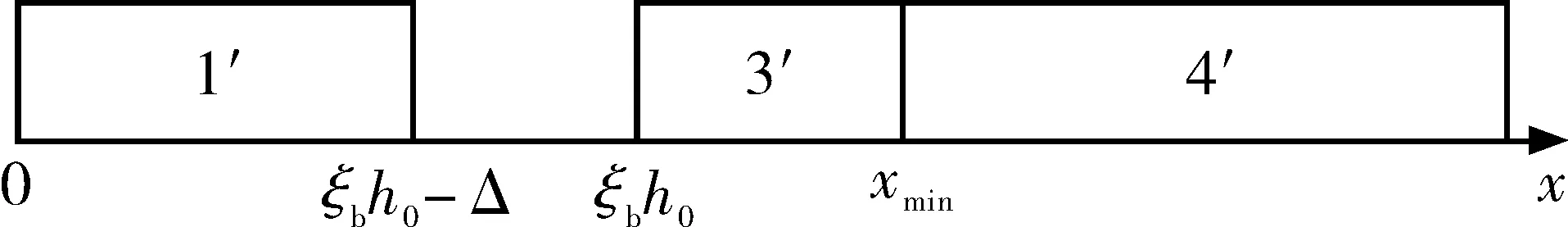
Fig. 7 Overall distribution of x3 算例分析——偏压构件承载力

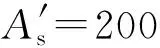
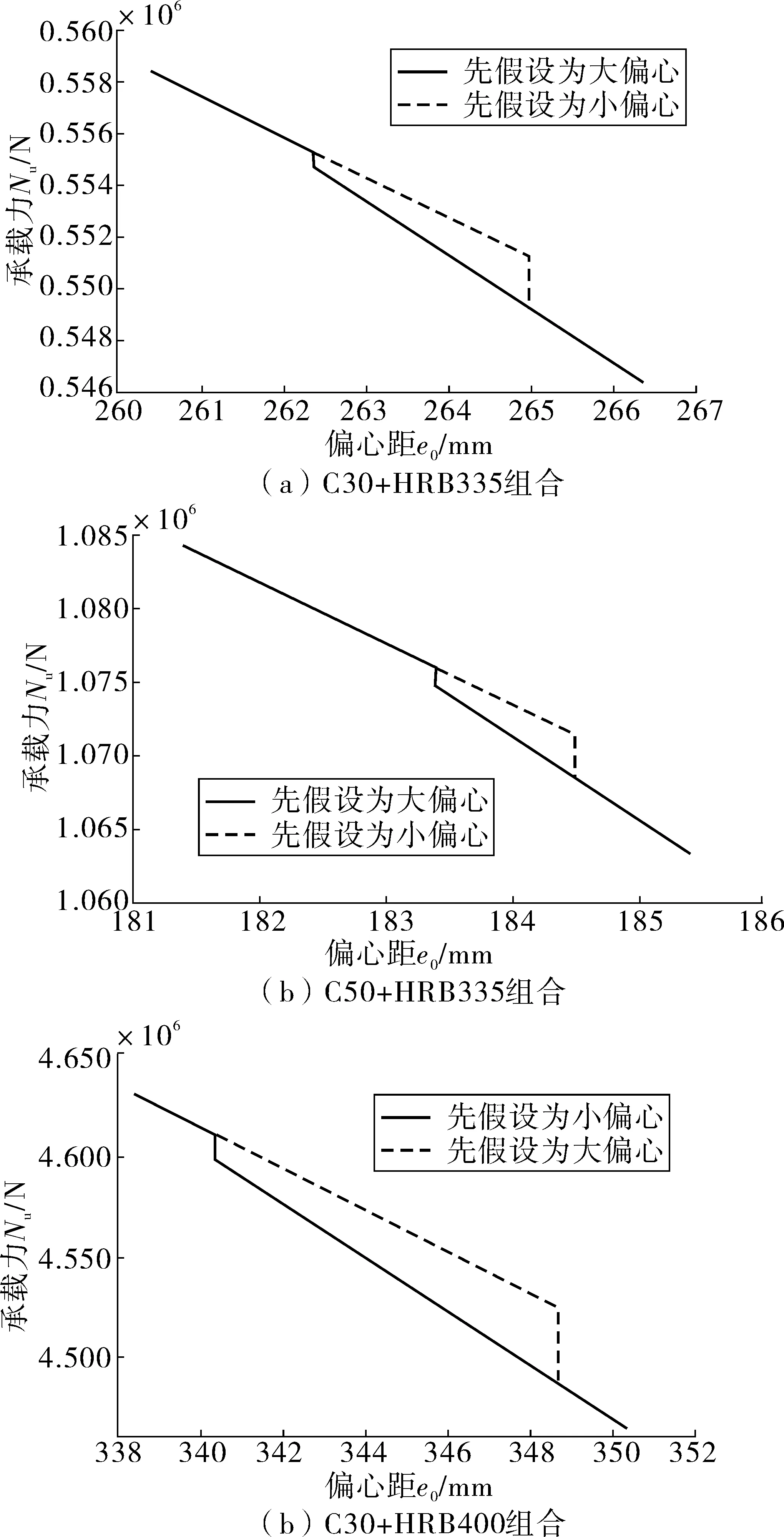
5 结 论
