设计效应分解在复杂样本设计中的应用研究

罗 薇

(广东工业大学 a.管理学院；b.大数据战略研究院，广东 广州 510006)

一、引言

自1965年Kish最早提出设计效应的概念以来，设计效应在复杂样本设计阶段起着非常重要的作用，通常利用设计效应和简单随机抽样下的方差来估计给定精度要求下的样本量[1]257-263。设计效应越大，意味所需的样本量越大才能达到简单随机抽样的效果，所以控制样本的设计效应，使得预计的样本量满足成本和精度的要求，是抽样设计领域的研究热点。实证研究发现，不同国家进行的相似调查中类似调查变量的设计效应值相近[2]；同一调查中样本均值和复杂分析统计量的设计效应值有一定关联[3]，这意味着可以将以往调查中某些调查变量的设计效应移植到新调查的类似调查变量中，将一些调查统计量的设计效应推广到同一调查的其它调查统计量上，在连续性调查中使用前期调查的设计效应信息来辅助现行调查设计。然而，另一些实证研究却发现，同一调查中的不同调查变量，以及连续性调查中同一调查变量的设计效应值可能存在较大的差异[2]，表明设计效应的直接扩展受到一定的局限。显然，如何将前期调查的设计效应信息用于现行调查设计，进而在抽样设计阶段根据设计效应来选择抽样方法，是设计效应应用于复杂样本设计的核心问题，而目前对此并没有进行系统的研究。为了弥补这一不足，本文对构成复杂样本的抽样方法进行分解，从单项抽样方法要素的视角来建立各种设计效应模型，分析单项要素对复杂样本设计效率的影响及应用局限性，推导要素组合的综合设计效应模型，基于设计效应模型的框架建立一套简单实用的复杂样本设计方法，进而研究设计效应在子群、不同调查变量、不同统计量间的扩展。在应用上，将上述设计效应模型应用于住户调查的样本设计，在样本设计阶段选择合理的抽样方法，使得估计的样本量能满足总体、域、子群的调查精度要求。

二、设计效应的分解与组合

(一)设计效应模型

根据Kish提出的设计效应概念，对于调查变量θ，Vc(θ)表示采用复杂抽样设计的估计量方差，Vsrs(θ)表示相同样本量下简单随机抽样的估计量方差，θ的设计效应为[1]257-263：

D2(θ)=Vc(θ)/Vsrs(θ)

(1)

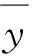
(2)

(二)设计效应的分解

为了明确复杂样本设计下哪些要素会导致设计效应，梳理复杂样本的基本特征如下：一是不同的抽样方式；二是被调查单位有不同的权数；三是不同子群的抽样比有差异[4]。同时依据联合国统计司的建议，将影响复杂样本设计的单项要素分为分层、类集(包括整群、二阶及多阶抽样)、加权调整三类[5]95-122。

1.分层的设计效应

对一阶分层抽样，忽略有限总体校正因子时，调查变量y的分层设计效应可以表示为[5]95-122：

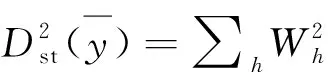
(3)

其中，从总体单位数N中抽取样本量n=∑nh，从单位数为Nh的第h层中抽取样本量为nh的总体单位，Wh=Nh/N为第h层的层权。

(4)

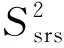
(5)

其中，wh=Nh/nh为初始权数。

一般来说，由于分层样本分布更为均匀，分层能减少样本中总体单位的相关性，从而减小方差，进而减小设计效应。但是，若各层均值大致相等，分层带来的精度改进较少，此时分层设计效应虽然小于1，但接近1。

2.类集的设计效应

(6)

其中，δ称为组内同质系数，描述初级抽样单元内变量y的同质性。实际中，初级抽样单元中总体单位的各个调查变量都有一定的相似性，但这种相似性往往较低，所以δ几乎总是数值较小的正数[5]。

(7)

通过对同质系数δ的演绎，可以将式(7)应用于PPS抽样和各种子样本设计方法组合的均等选择概率设计下类集设计效应的计算。

现实中由于初级抽样单元的规模不等以及规模信息不准确，往往采用与估计规模成比例的概率抽样方法(Probability to Proportional to Estimated Size，简称PPES)抽取初级抽样单元，此时要满足均等选择概率样本的要求，则从各样本初级抽样单元中抽取的总体单位数b不等。当各个子样本规模差异不大时，式(7)仍可以计算类集的设计效应，但是b表示平均子样本规模，即：

(8)

(9)

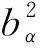
由于同质系数δ是正数，所以类集的设计效应总是大于1。在实际工作中，出于成本的考虑，类集规模b不适宜设计较小，导致类集的设计效应一般较大。上述分析还展示出各阶段抽样方法的选择如何影响到δ和b的确定，进而引起类集设计效应的变化。其中，δ是内生的。经验研究表明，调查变量和初级抽样单元相同或相似时，δ值具有较好的移植性[2]，可以通过以往调查中相同或类似变量以及初级抽样单元的信息来估计δ。但直接将历史调查的类集设计效应用于新的调查设计并不合理，因为每个调查变量的δ值都不一样，b较大时，各个调查变量的δ值即使只有细微的差别，也会引起类集设计效应的较大差异。例如，δ=0.05，b=30时，类集的设计效应值为2.45；δ=0.08，b=30时，类集的设计效应值高达3.32。

3.加权调整的设计效应

上文的设计效应分析基本上限于均等选择概率抽样设计，最终抽样单元的权数相等，然而不均等选择概率的情形也存在，当抽样设计偏离均等选择概率，需要对初始权数(抽样概率的倒数)进行规模调整或是结构调整，此时最终权数在某种程度上总是有差异的[9]。

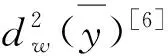
(10)

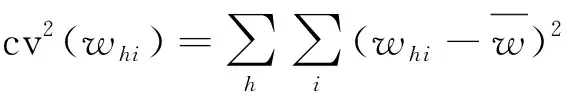
由于特殊因素、无回答、抽样框缺陷等情形对权数变动的影响是偶然的、随机的，总体单位权数wj(j=1，2，…，n)将会带来精度的损失，这个损失可以用权数wj的相对方差来表示，得出比式(10)更一般的形式：

=1+cv2(wj)

(11)

如果权数和调查变量无关，则式(11)表示的不均等加权的设计效应，可以从一个调查变量扩展到其它调查变量。但是，如果权数通过事后分层或是根据某些外部来源的已知控制总量的校准获得时，当目标变量与这些控制总量高度相关，则权数的调整显然可以改进精度，而式(11)却表现出精度的损失，将高估权数调整的设计效应，这时式(11)不再适用。

(三)要素组合的设计效应

1.分层和类集的组合

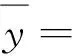
(12)

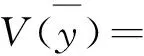
(13)

(14)

(15)

2.类集和加权调整的组合

在类集和不等概率抽样方法组合的复杂样本中，Kish提出在权数随机或近似随机的情况下设计效应模型近似为[10]：

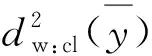
(16)

3.分层、类集和加权调整的组合

在分层、类集和不等概率抽样方法组合的复杂样本中，总体均值的加权估计量可以表示为：

(17)

其中，从第h层抽取a个类集，bhβ是第ahα个类集的总体单位数。Gabler等在各小域方差相等，但各小域同质系数不等的假设下推导出不重叠的完备域的设计效应[11]，本文用层替代小域，则可以得到式(17)的设计效应：

(18)

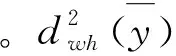
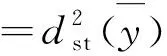
(19)

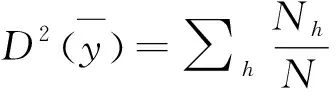
(20)

将以上种种综合起来，可用图1示之。

图1 设计效应的分解与组合图

三、子群和分析统计量的设计效应

许多调查会深入到子群，因而需要计算子群描述性统计量以及复杂分析性统计量的设计效应，这些设计效应都可以由样本均值(比例)的设计效应来进行扩展。

(一)子群的设计效应

根据子群在初级抽样单元中的分布情况，可以将子群分为两类：第一，子群在初级抽样单元中均匀分布，称为交叉类(Cross Classes)，人口、社会、经济的众多分类都属于交叉类，如年龄、性别、教育程度、职业子群。第二，子群集中在由若干个初级抽样单元构成的集合中，称为分割类，如行政区子群、农村和城市子群。

如果子群中权数的分布近似总样本，则可以直接从总样本来推导子群估计量的加权调整设计效应，即交叉类和总样本的加权调整设计效应几乎一样，所以下面只考虑子群的类集设计效应。

1.交叉类的设计效应

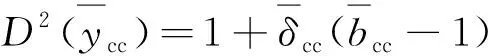
(21)

(22)

其中kd>1，且随着交叉类规模变化。由于社会经济子群比人口子群的变化大些，更容易聚集，同质性系数也大些，Kish通过总结大量的调查实践，建议kd值取1.2(人口子群)或1.3(社会经济子群)[3]。

2.分割类的设计效应

(二)分析统计量的设计效应

1.子群均值之差的设计效应

随着调查数据质量的提高，对分析统计量的关注越来越多，最常见的分析统计量即两个子群的均值(比例)差或比值。下文先分析两个独立样本均值之差的设计效应：

(23)

如果两个样本均值的设计效应、样本量类似，则它们差的设计效应等于它们各自设计效应的加权平均，ni(i=1，2)表示样本量，对应的权数为1/ni，当两个样本来自同一调查的不同时期，两个样本间的协方差将降低其差的设计效应：

(24)

当两个样本来自相同类集(如初级抽样单元、次级抽样单元、最终抽样单元)，则式(24)中协方差为正，使得均值之差的设计效应变小。Kish研究发现，两个子群均值之差的设计效应大于1，但是小于假设两个子群均值独立时的设计效应[3]。将上述结论表示成方差形式有：

(25)

当子群是交叉类时，式(25)正协方差效应使得均值之差的设计效应变小，实证研究表明，协方差的影响作用相当大，使得交叉类子群均值之差的设计效应只比1大些许[3]。当子群是分割类时，协方差的效应不明显，假设两个子群总体单位方差相等，则式(25)简化为：

(26)

2.其它复杂分析统计量的设计效应

其它分析统计量，如均值比、中位数、分位数、线性回归系数等，直接计算其设计效应相当困难，但是根据一系列分析统计量设计效应的实证研究(见表1)可以归纳出一些规律[12]。

表1 三个复杂样本中5种估计量的设计效应值

注：数据来源于Kish和Frankel[12]。

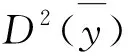
(27)

四、案例分析

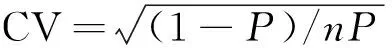
第一步，明确各省的样本量分配。表2给出了3种样本分配方案：比例分配、常数分配、折中分配。由于各省规模差异较大，3种样本分配方案截然不同。比例分配下，小省的样本量太少，难以产生可靠的估计值；而常数分配则降低了全国估计的精度；折中分配与比例分配相比，小省的样本量增加了，但是没有按常数分配增加得多。采用比例分配时，分层的设计效应为0.99；由于全国大型住户调查中，层方差、层均值大致相等的假设是合理的[5]，由式(3)得到常数分配的分层设计效应为1.93；由式(5)，折中分配产生的不等概率加权设计效应为1.21。

表2 三种样本分配下各省样本量分配情况

第三步，综合考虑类集设计效应和各省样本量非比例分配的设计效应。根据式(16)，采用折中分配时，全国样本的设计效应即1.21×1.95=2.36，则全国有效样本量为10 000/2.36=4 237，全国社保未覆盖率估计量的变异系数为0.027，显然，全国估计量的样本量超过给定的精度要求；采用常数分配时，设计效应为1.93×1.95=3.76，有效样本量为2 660，全国社保未覆盖率估计量的变异系数为0.034，不能满足样本设计全国估计量变异系数的要求。

按照上述思路可以计算出关键调查变量的可能精度，依据设计要求修改样本量。如果存在无回答、覆盖不足的情况，还要考虑调整权数对设计效应的影响，例如全国的回答率大约为90%，则样本量还需要增加11%。

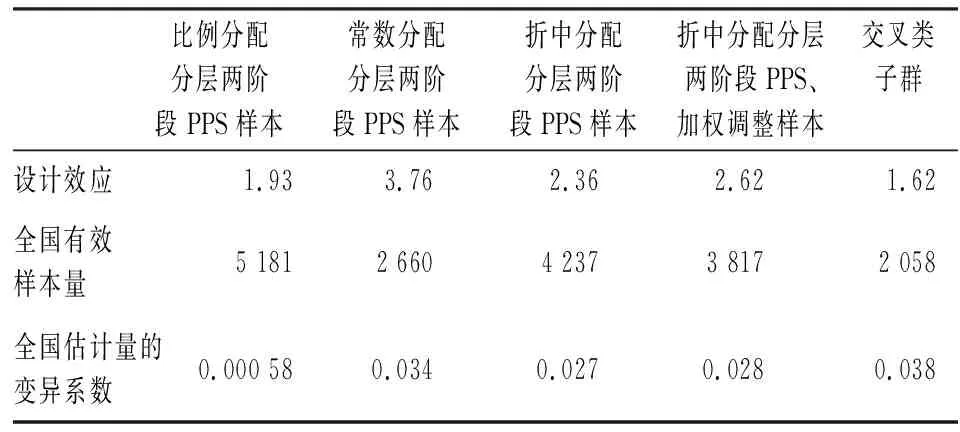
表3 抽样方法组合设计效应的比较结果

比较表3数据的模拟结果可发现，按比例分层两阶段PPS样本的设计效应最小，0.99×1.95≈1.93，但这种分配方式对规模较小的省份不利，例如第10个省份在比例分配下，100户的有效样本量为100/1.93≈52，该省社保未覆盖率的变异系数为0.24，远不能达到分省变异系数的要求；采用常数分配所产生的非比例分层的设计效应较大，与类集设计效应组合后，综合设计效应为3.76，相应的有效样本量仅仅为2 660户，变异系数不能满足全国要求；而介于比例分配和常数分配之间的折中分配，即使考虑无回答、不覆盖所导致的加权调整设计效应，仍可能满足全国和分省估计量的精度要求；对于总体的交叉类子群，由于类集设计效应的显著降低，折中分配分层两阶段PPS 样本下的有效样本量仍可以为子群提供较为精确的估计。

五、结论与启示

本文将影响复杂样本设计的单项要素分为分层、类集、加权调整三类，以此为基础，将综合设计效应分解成要素的设计效应，研究结论表明复杂样本设计导致总体单位间相关性的变化，进而影响总体方差及设计效应：分层设计带来的总体单位间负相关性将减少方差及设计效应，但是总体单位分层带来的精度改进十分有限，而各层样本量的非比例分配引起的权数差异将引起设计效应的增加；类集设计带来较大及正的总体单位间相关将引起设计效应的显著增加，由于影响类集设计效应的同质系数具有一定的扩展性，类集设计效应可以扩展到不同子样本抽样方法、子群、复杂分析统计量设计效应的计算；当权数和调查变量无关，不均等加权的设计效应也可以从一个调查变量扩展到其它调查变量；对于子群均值及其差值、复杂分析统计量，各种抽样方法引起的总体单位间相关性减弱，所以其设计效应也相对较小。

本文得出启示：第一，由于综合设计效应反映了多种抽样方法结合的影响，应用时要分解为单项要素设计效应；第二，由于各种抽样方法通过影响总体单位的相关性来影响设计效应，描述群内相关性的同质系数非常重要，在样本设计阶段使用设计效应模型就需要估计出同质系数，鉴于同质系数的可移植性，往往用历史调查中相同或类似变量以及初级抽样单元的信息来估计关键目标变量的δ值；第三，设计效应在样本设计阶段中发挥重要作用，理解非比例分配和类集设计对调查变量精度的影响是进行有效样本设计的关键。