大宗商品期货价格极端波动风险与演化模式研究——基于供给侧结构性改革视角

郭文伟，刘英迪，袁 媛，张思敏

(广东财经大学 金融学院，广东 广州 510320)

一、引言

大宗商品一般是指可进入流通领域但非零售环节，具有商品属性用于工农业生产与消费的物质商品。中国大宗商品期货主要包括能源化工、工业、金属、贵金属、农产品等5种商品期货，涉及国民经济中工农业生产与消费的诸多领域。自2015年11月供给侧结构性改革实施以来，随着“三去一降一补”的持续推进，中国农产品、有色金属、能源化工产品等大宗商品供需关系及结构均发生了深刻转变，价格波动频率及幅度趋向增大，不仅影响了下游相关行业的生产经营，也易造成上游行业供给和产量的反复，破坏了供给侧结构性改革的已有成果。作为大宗商品市场的一个重要组成部分，大宗商品期货市场具有价格发现及套期保值的重要功能，但与此同时，高杠杆性又使其更易发生极端波动，进而对现货市场产生严重冲击。那么，供给侧结构性改革是否会增强中国大宗商品期货价格的极端波动及其市场风险走势呢？在当前深入推进供给侧结构性改革的新时代背景下，这是亟待研究的重要课题。关于这个问题的研究，一方面能够揭示中国大宗商品价格极端波动风险程度及其演化模式；另一方面也能科学评价供给侧结构性改革对大宗商品期货市场波动的影响，进而为优化现有供给侧结构性改革政策和避免引发市场极端风险提供有益的借鉴，最终为巩固供给侧结构性改革已有成果及保证实体经济稳健运行提供决策支持。

二、文献综述

(一)大宗商品价格极端波动风险测度的研究现状与评价

较早的金融市场风险测度方法为风险价值(VaR)模型，该模型能衡量一定时期内一定置信水平下某一资产的最大可能损失，在金融机构的风险管理实践中应用广泛。之后，有学者将单变量VaR模型进一步拓展为3大类不同的风险测度模型：参数类(RiskMetrics、GARCH族模型等)、非参数类(蒙特卡罗模拟法、历史模拟法等)、半参数类(CAViaR模型等)。由于非参数类模型可能造成信息损失和维数灾难，因此实践中更多采用参数类模型及半参数类模型对VaR进行测度。大量实证研究表明，大宗商品期货收益率序列通常具有尖峰厚尾、波动聚集、自相关性和杠杆效应[1]，未能满足传统VaR测度方法的假设条件，因此国内外学者主要采用GARCH族模型及CAViaR族模型对其风险进行刻画，并进行了两方面的对比研究：一方面，庞淑娟和刘向丽、Musunuru等对比了若干GARCH族模型对不同商品期货风险的测度能力后认为，考虑了长记忆性的HYGARCH模型、长记忆性及杠杆效应的FIGARCH(1，d，1)模型和FIEGARCH(1，d，1)模型、考虑不对称性的EGARCH模型，具有更佳的风险预测能力[2-3]。

在大宗商品价格极端波动风险测度方面，现有研究主要集中于ARMA-GARCH-EVT模型的创新及应用上，这一模型的建模思路是：首先，通过ARMA-GARCH模型对具有波动集聚的原始收益数据进行过滤，获得条件均值、条件方差与满足独立同分布的标准残差序列；其次，应用EVT模型对标准残差序列建模并计算出考虑极端事件的极值分位数；再次，将条件均值、条件方差、极值分位数相结合计算出极端风险。国内外学者基于这一思路将不同GARCH族模型与EVT理论结合进行了实证研究。Zhang等运用EGARCH-POT模型分别测度了贵金属及欧盟碳市场的价格波动，实证结果表明所构建模型具有良好的拟合效果[4]；Youssef等构造了多个GARCH-EVT模型对能源期货的动态风险进行度量，发现HYGARCH-EVT模型和FIAPARCH-EVT模型在极端VaR测度中表现更好[5]；胡宗义等通过构建Expectile-EVT模型测度国际原油的极端波动风险[6]，虽然ARMA-GARCH-EVT模型对原始收益数据进行了过滤，但是仍需假设收益分布并选择条件方差方程，实证中对这些问题并未产生共识。针对上述问题，Engle和Manganelli提出了CAViaR模型，并结合极值理论EVT构建了CAViaR-EVT模型[7]。从理论上看，CAViaR-EVT模型能够结合CAViaR处理普通分位数及EVT测度极端风险的优点，在极端尾部风险度量及其演化模式刻画方面更具优势，但至今这一模型在实践中运用极少，目前仅有张晨等将其运用于国际碳市场的极端风险测度[8]；简志宏等将其运用于大宗商品期货市场的极端风险测度，并显示出这一模型在大宗商品价格极端波动风险测度方面的潜力[9]。与此同时，在大宗商品期货价格极端波动风险研究方面依然存在如下不足：一是现有研究集中关注极端下尾风险，而较少同时关注极端上尾风险，在期货市场中极端上尾风险依然是做空的投资者需要重点关注的问题；二是现有研究一般只关注某一具体品类大宗商品价格波动风险，而鲜有对整个大宗商品期货市场及现有各类商品期货价格的极端波动风险进行系统性测度与比较；三是鲜有文献专门研究大宗商品期货市场的风险演化模式及其差异。

(二)供给侧结构性改革影响大宗商品价格极端波动风险的研究现状与评价

供给侧结构性改革政策出台前，国内学者在大宗商品价格，尤其是国际大宗商品价格极端波动的影响因素方面已形成了较为丰富的研究成果。马龙等认为，货币供给通过影响通胀预期进而影响大宗商品价格波动，并提倡政府注重对全社会通胀预期的调控[10]；韩立岩、张峻晓等学者认为，短期内投机行为是大宗商品期货价格极端波动的重要推手[11-12]。

供给侧结构性改革政策出台至今，国内系统研究其对大宗商品价格极端波动影响的文献较为缺乏，国外几乎没有。郭俊华等对供给侧结构性改革的内涵、目标和路径进行了系统性阐述[13]；吕炜等认为供给侧层面因素通过价格自循环效应及市场势力两条途径影响上游行业价格的极端波动，提出政府在供给侧结构性改革中应引入上游行业的竞争机制，避免上游行业市场势力重新增长及价格自循环效应的不利影响使供给侧结构性改革已有成果遭到破坏[14]。然而，对于2012年以来，尤其是2016年下半年至今中国大宗商品价格极端波动的成因，诸多学者及研究员的观点不一，尚未形成共识。

总体而言，研究大宗商品价格波动影响因素的文献较为丰富，但现有文献较少对供给侧结构性改革前后大宗商品期货价格极端波动风险进行测度与比较，也鲜有研究大宗商品期货市场风险演化模式的变迁。与已有文献相比，本文研究特色表现为：一是综合考虑极端下尾与极端上尾风险，分析大宗商品期货投资者的多头下跌风险与空头上涨风险；二是构建CAViaR-EVT-VaR模型测度大宗商品期货极端波动风险及其演化模式，并通过与ARMA-GARCH-EVT-VaR模型进行综合比较，进一步突出CAViaR-EVT-VaR方法的建模优势；三是比较供给侧结构性改革前后各类大宗商品期货价格波动特征及其极端风险的变化，进而评价供给侧结构性改革对大宗商品价格波动的影响机制，并提出防范对策。

三、理论模型构建与说明

(一)CAViaR模型及参数说明

由于文章篇幅限制，这里仅介绍CAViaR模型及其参数含义，而对于本文采用的ARMA模型及传统GARCH族模型(GARCH、EGARCH、HYGARCH、FIAPARCH)则不再重复阐述。Engle和Manganelli提出了4种经典CAViaR模型：

1.对称绝对值模型SAV：

VaRt(p)=β0+β1VaRt-1+β2rt-1

(1)

2.不对称绝对值模型AS：

VaRt(p)=β0+β1VaRt-1+β2(rt-1)++

β3(rt-1)-

(2)

3.间接GARCH模型IG：

(3)

4.适定性模型AD：

VaRt(p)=VaRt-1+

β1[1+exp(G[rt-1+VaRt-1])-1-θ]

(4)

其中rt-1为历史对数收益率系列；θ为置信水平，一般取1%或5%；G为一有限的正数，这里取为10，当G→∞时式(4)右边的最后一项趋于[1-(xt-1≤-VaRt-1)-θ]，其中I(·)为提示性函数；当G为有限正数时，该模型将为光滑的阶梯函数。从式(4)可看出，第t期的在险价值VaR将受到第t-1期的历史收益率rt-1的影响；与此类似，SAV与IG模型均考虑了这种情况。

(二)EVT模型及参数说明

极值理论可分为BMM模型和POT模型，BMM模型将观测数据按时间顺序等分为互不重叠的若干区间，并对每个区间的最大值组成的数据序列建模；而POT对观察值中超过某一较大阈值的数据建模，由于POT模型有效使用了有限的极端观察值，通常被认为在实践中最为有用[15]，因此本文主要介绍POT模型。

假设观测值序列为X1，X2，…，Xn，对于一个合理的阈值u，超过阈值的Nu个样本对应的超额数序列为Yi=Xi-u(i=1，2，…，Nu)，则超额数Y的分布函数为：

Fu(y)=Pr(X-u≤y|X>u)

(5)

对于一个充分大的阈值u，Fuy可以用广义帕累托分布逼近，即：

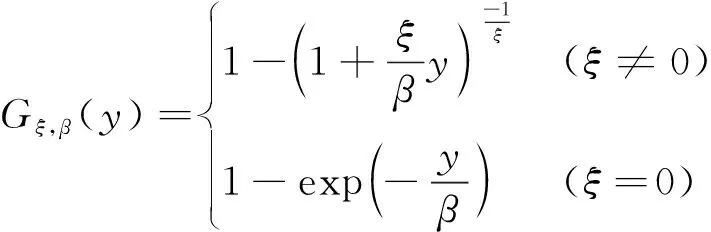
(6)

设x=u+y，则分布的尾部累积分布函数为：

F(x)= (1-F(u))Gξ，β(x-u)+F(u)

(x>u)

(7)

令F(u)=(n-Nu)/n，并用极大似然法估计GPD分布的形状参数ξ和尺度参数β，则有：

(8)

对于置信度p>F(u)的尾部估计，反解上式可得到p分位数：

(9)

(三)ARMA-GARCH族-EVT-VaR模型构建及参数说明

GARCH族模型采用如下离散化形式，刻画金融资产损失序列的动态过程：

Rt=μt+εt=μt+σtzt

(10)

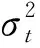
(11)

结合上述关于ARMA、GARCH族、EVT模型的介绍以极端多头VaR为例，ARMA-GARCH族-EVT-VaR模型的构建可分为如下3个步骤：

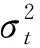
步骤3：将μt、σt、Qp(Z)代入式(11)计算VaRtp(R)。

计算极端空头VaR时采用收益率序列，按上述同样步骤即可完成。

(四)CAViaR-EVT-VaR模型构建及参数说明

CAViaR-EVT-VaR模型的构建思路是通过POT方法将CAViaR计算得出的正常分位点分位数转化为极端分位点分位数，以极端多头VaR为例，模型的构建可分为如下4个步骤：

步骤2：通过式(12)计算标准化残差序列。

(12)

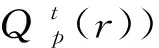
(13)

步骤4：通过式(9)计算出标准化残差序列的(1-p)分位数，代入下式可计算出损失率序列的p分位数，即100(1-p)%置信水平下的VaR。

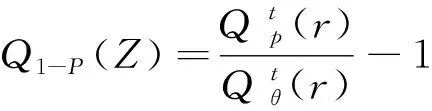
(14)

计算极端空头VaR时采用收益率序列，按同样的步骤即可完成。

本文采取传统的LR检验以及Engle和Manganelli提出的DQ检验对上述ARMA-GARCH族-EVT-VaR模型及CAViaR-EVT-VaR模型的精确度进行检验，由于论文篇幅限制，具体细则不再详述，可参见相关文献说明。

四、实证分析

(一)样本选取及描述

本文以南华期货商品指数报告的综合指数(ZH)、工业品指数(GY)、能化指数(NH)、金属指数(JS)、贵金属指数(GJS)、农产品指数(NCP)为研究对象，其中综合指数反映了中国整个大宗商品期货市场的状况；样本期为2012年9月6日至2017年9月15日，基本包含了供给侧结构性改革政策出台(2015年11月)的前后两年左右时间，剔除样本期内未报告指数数据的天数，共获得1 216个日度数据和1 215个对数收益率及损失率数据(数据均来自于东方财富Choice数据库)；对数收益率rt及损失率Rt计算公式如下，其中Pt和Pt-1分别为各类商品期货指数在第t日和第t-1日的收盘价：

rt=100×ln(Pt/Pt-1)

(15)

Rt=-100×ln(Pt/Pt-1)

(16)

表1是各种大宗商品期货收益率序列的描述性统计结果，从中可以看出：综合类、工业类、能化类、金属类大宗商品期货收益率序列均值为正值，而贵金属类与农产品类大宗商品期货收益率序列均值为负值；6种大宗商品期货指数收益率序列的峰度均超过3，具有尖峰特征；综合类、工业类、能化类、贵金属类的偏度小于0，具有左偏特征；金属类和农产品类的偏度大于0，具有右偏特征。结合JB检验结果可以看出：6种收益率序列均在1%的显著性水平上拒绝正态分布的原假设，说明这些大宗商品期货价格收益系列均不服从正态分布；平稳性ADF检验结果显示：6种收益率序列均在1%的显著性水平下拒绝非平稳的原假设，均为平稳序列；Ljung-Box Q(20)统计量结果显示：在滞后期为20时，综合类、工业类、金属类收益率序列存在长阶自相关性，能化类、贵金属类、农产品类收益率序列不存在长阶段自相关性；从波动率来看，能化期货、金属期货和贵金属期货的价格波动相比其他大宗商品期货价格波动更为激烈，而农产品期货价格波动率相对较小。

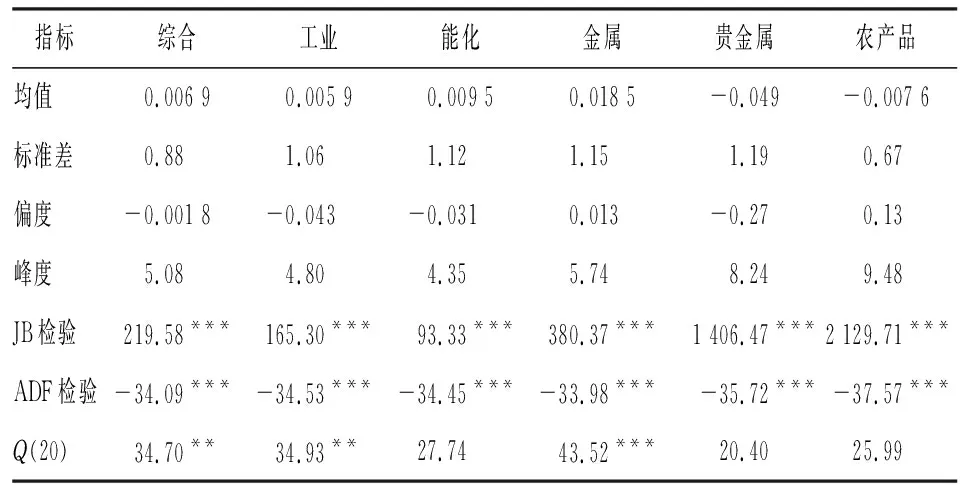
表1 各种大宗商品期货指数收益率序列的描述性统计特征表

注：*、**、***分别表示在10%、5%、1%的显著性水平上显著，下表同。

(二)ARMA-GARCH族模型与CAViaR模型的拟合效果评价

由于金融计量中一阶模型已经能够较为充分地反映金融时间序列的波动特征和自相关性，因此本文选择简单的ARMA(1，1)、GARCH(1，1)、EARCH(1，1)、HYGARCH(1，d，1)、FIAPARCH(1，d2，1)模型对样本数据进行拟合。表2是ARMA-GARCH族模型的参数估计结果，可以看出对于全部6种大宗商品期货收益率序列，ARCH参数φ和GARCH参数β均显著，且两者之和小于1，条件方差方程收敛，说明波动具有持续性；除综合类收益率序列外，其他5种收益率序列的HYGARCH模型、FIAPARCH模型中参数d均大于0而小于1，且多在5%的置信水平上显著，说明这5种收益系列具有长记忆性；6种收益率序列在FIAPARCH模型中参数γ均不显著，说明杠杆效应不明显。另外，从最大似然值来看，这4类GARCH族模型的拟合效果并无显著优劣，而FIAPARCH模型在6种收益率序列中最大似然函数值往往相对更大，说明更适合对这些大宗商品期货进行波动率建模分析。

表2 ARMA-GARCH族模型参数估计结果表(基于训练样本)

本文参考Engle和Manganelli的做法，将时间序列后500个样本作为检验样本，其余样本作为建模样本，并通过RQ值、建模样本Hit值和DQ检验P值分析CAViaR模型拟合情况。表3是4种CAViaR模型在5%分位数下的参数估计结果，从样本内Hit值和DQ检验P值可以看出，除AD模型在测度综合类、能化类、金属类大宗商品空头VaR时出现P值小于显著性水平0.05而被拒绝外，其余3个CAViaR模型在6种大宗商品多、空头VaR测度时均未出现被拒绝的情况，整体表现较好；从RQ值来看，综合考量多头VaR、空头VaR的表现可知与其余模型相比，AS模型在多数大宗商品的VaR测度中表现更好。进一步，考察各模型参数估计结果可以发现，自相关系数β1基本均显著(除综合类大宗商品空头VaR下的IG模型)，说明尾部分位数存在波动集聚现象，且工业类、金属类、农产品类大宗商品前期VaR对市场的影响相对更大；多数情况下系数β2与β3在空头VaR中比在多头VaR中更为显著，说明空头方对外部信息的冲击更为敏感。总体而言，从训练样本来看，GARCH族模型中的FIAPARCH模型与CAViaR模型中的AS、IG、SAV模型均能较好地拟合收益率与损失率序列或其VaR序列。

表3 CAViaR模型在5%置信水平下的参数估计结果表(基于训练样本)

(三)ARMA-GARCH族模型与CAViaR模型标准化残差的POT估计结果

本文选取时间序列的90%分位数作为阈值，并采取极大似然法估计GPD分布的形状参数ξ和尺度参数β。表4、表5分别报告了ARMA-GARCH族模型和CAViaR模型标准化残差序列的POT估计结果，从中可以看出在对GARCH族模型标准化残差进行拟合时，综合类、工业类标准化残差序列具有显著的厚尾性，金属类标准化残差序列具有显著的短尾性，而贵金属类标准化残差序列的左右尾则有不对称性；在对CAViaR模型标准化残差进行拟合时，能化类标准化残差序列具有显著的短尾性，农产品类标准化残差序列具有显著的厚尾性，而其余4种大宗商品标准化残差序列则具有显著的不对称性。

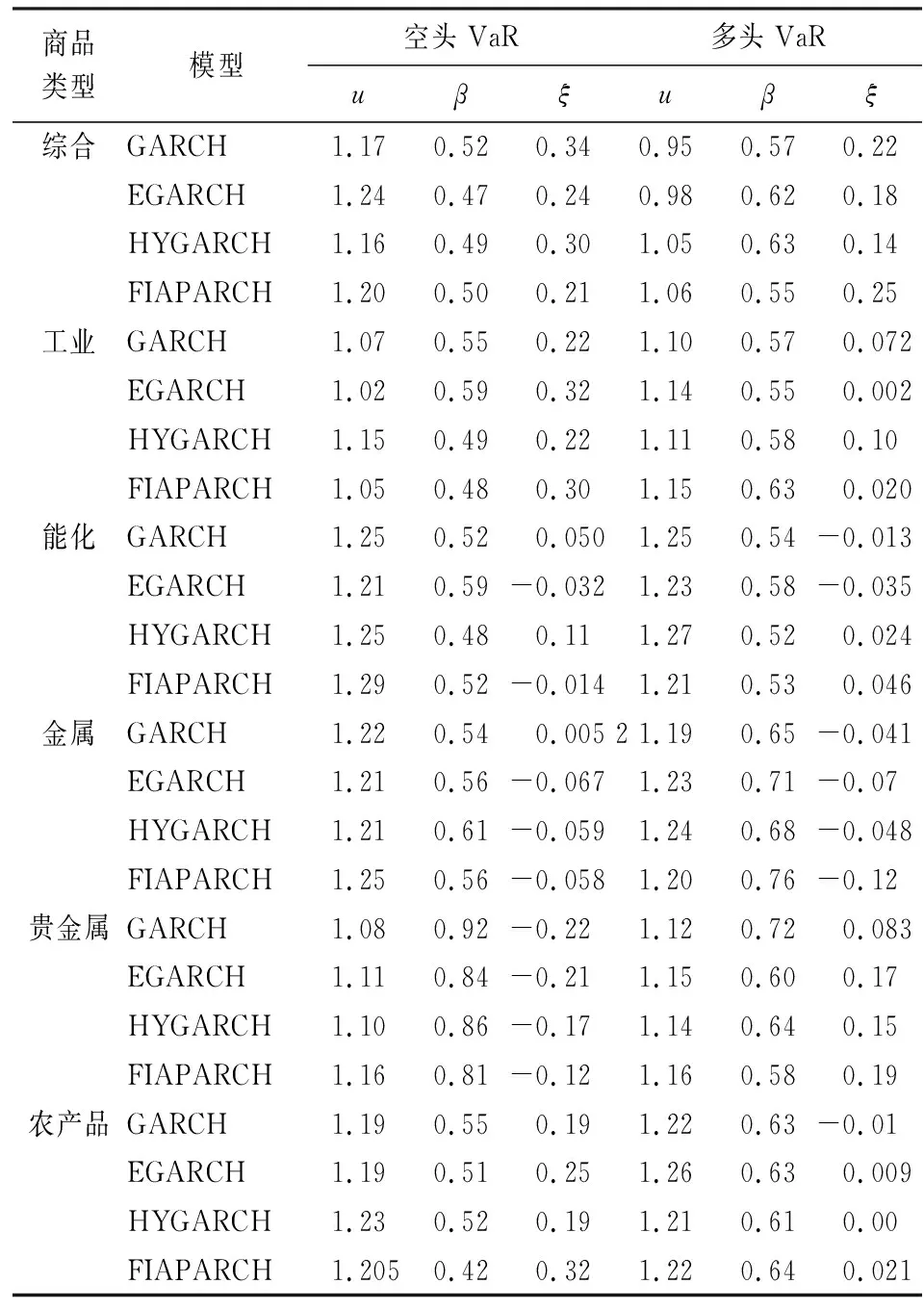
表4 ARMA-GARCH族模型标准化残差序列POT估计结果表

表5 CAViaR模型标准化残差序列POT估计结果表

(四)基于ARMA-GARCH族-EVT模型与CAViaR-EVT模型极端风险预测比较

通过POT估计出标准化残差序列的形状参数ξ及尺度参数β后，可计算标准化残差序列的极端分位数，进而根据其与收益率序列或损失率序列极端分位数的关系，求解出收益率或损失率序列的极端分位数。本文在测度极端空头风险时采用各大宗商品期货的收益率序列，在测度极端多头风险时采用各大宗商品期货的损失率序列。表6报告了各种ARMA-GARCH族-EVT模型与CAViaR-EVT模型在5%显著性水平上6种大宗商品期货极端多、空头VaR测度的LR检验P值及失败率；由于LRcc检验综合考量了LRuc检验与LRind检验，因此以下比较主要参考LRcc检验P值及失败率，并辅以LRuc及LRind检验，结果显示总体上看CAViaR-EVT模型的精确度高于ARMA-GARCH族-EVT模型，且两类模型预测极端多头VaR的精确度高于极端空头VaR。

对综合类大宗商品期货而言，4个GARCH族-EVT模型在极端多、空头VaR预测中均未通过LRcc与LRuc检验，且失败率显著高于CAViaR-EVT模型；而在4个CAViaR-EVT模型中，SAV-EVT模型通过了所有LR检验，在极端空头VaR预测中也具有较高的精确程度，是综合类大宗期货商品价格极端风险测度的最优模型。由于综合类代表了整个大宗商品期货市场的整体情况，由此说明中国大宗商品期货市场价格极端波动风险适合采用SAV-EVT模型进行测度。

对工业类大宗商品期货而言，4个GARCH族-EVT模型在极端多、空头VaR预测中同样均未通过LRcc与LRuc检验，且失败率显著高于CAViaR-EVT模型，而在CAViaR-EVT模型中，也仅有IG-EVT模型与AD-EVT模型同时通过了两个LRcc检验，相较而言AD-EVT模型的P值更大且失败率接近理论水平1%，是工业类大宗商品期货价格极端风险测度的最优模型。

对能化类大宗商品期货而言，GARCH族-EVT模型在预测极端多头VaR时具有更大的P值，但是失败率为0，有高估风险的可能，同时和其他3个GARCH族-EVT模型一样在极端空头VaR预测中未能通过LRcc与LRuc检验，不是最优的风险预测模型；在CAViaR-EVT模型中同样仅有IG-EVT模型与AD-EVT模型通过了两个LRcc检验，而AD-EVT模型具有更大的P值且失败率更接近理论水平1%，是能化类大宗商品期货价格极端风险测度的最优模型。

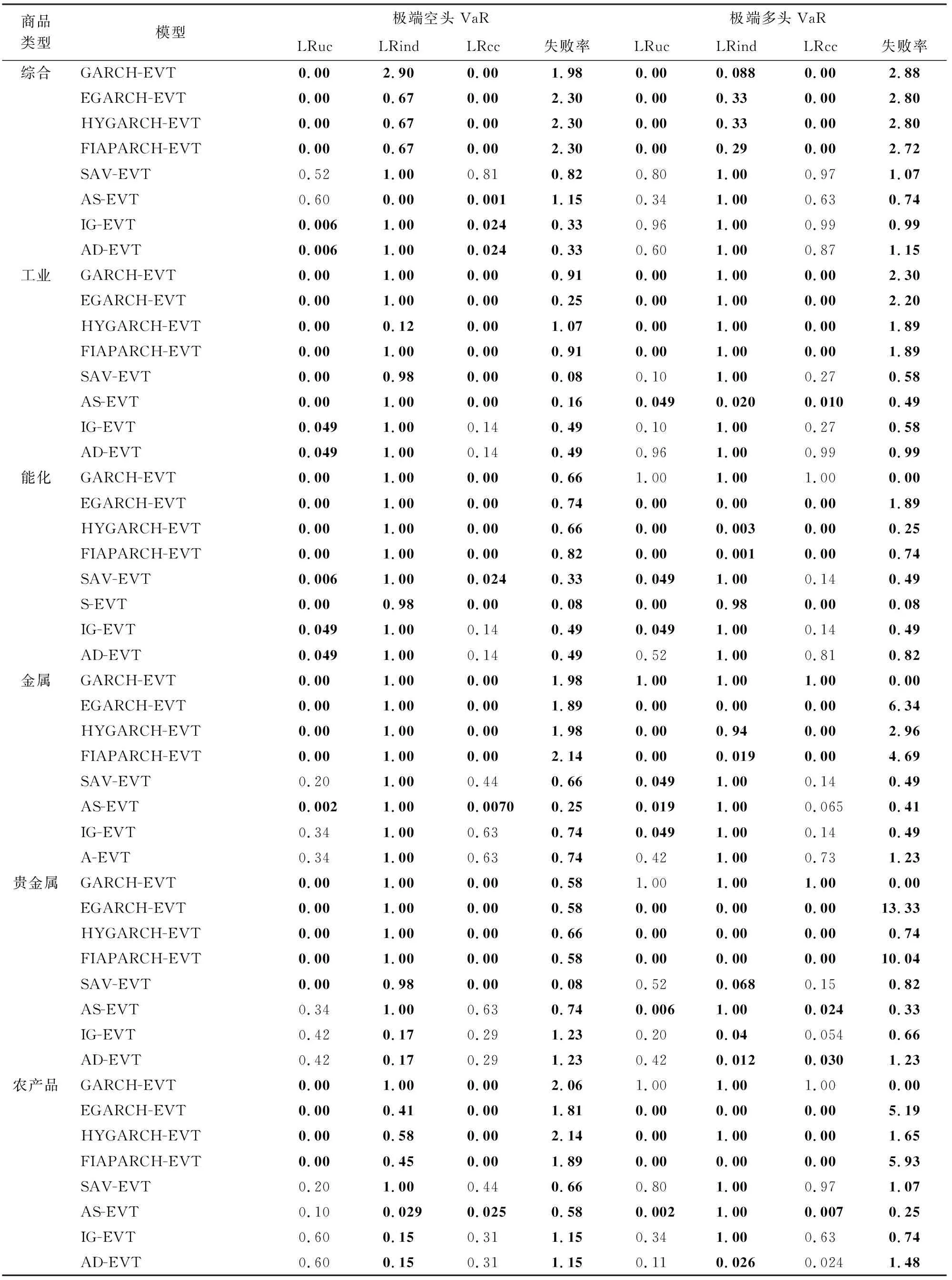
表6 1%分位数5%显著性水平上的LR检验结果表(基于检验样本)

注：表中数据表示LR检验的P值，其中加粗字体表示在95%的置信水平下拒绝该模型。

对金属类大宗商品期货而言，有SAV-EVT、IG-EVT、AD-EVT3个模型同时通过了两个LRcc检验，相较而言AD-EVT模型在极端多、空头VaR预测时均有较高的P值且失败率更接近理论水平1%，是金属类大宗商品期货价格极端风险测度的最优模型。

对贵金属类大宗商品期货而言，仅有IG-EVT模型通过了两个LRcc检验，是贵金属类大宗商品期货价格极端风险测度的最优模型。

对农产品类大宗商品期货而言，有SAV-EVT和IG-EVT两个模型通过了两个LRcc检验，两者的失败率与1%的理论水平均相差不大，但SAV-EVT模型在极端多、空头VaR预测时有相对更高的P值，是农产品类大宗商品期货价格极端风险的最优测度模型。

(五)供给侧结构性改革前后大宗商品价格极端波动风险比较

经过LR检验的比较，得出了每种大宗商品期货价格波动极端风险的最优测度模型。图1展示的是基于最优测度模型对各种大宗商品期货在1%置信水平上的极端多、空头VaR风险测度结果。从图1中可看出：以2015年第三季度为界，大宗商品期货价格波动情况可大致分为两个阶段：第一个阶段为2012年9月至2015年7月，这一阶段贵金属类大宗商品价格波动幅度较大，极端行情出现较多，而其他5种大宗商品价格波动则较为平缓，极端行情出现较少；第二个阶段为2015年7月至2017年9月，这一阶段贵金属类大宗商品期货价格波动幅度趋小，极端多头VaR与极端空头VaR走势较为平稳，而其他5种大宗商品价格波动幅度及频率则趋向增大，多头VaR与空头VaR水平均有升高。总体来看，贵金属类大宗商品期货与其他5种大宗商品期货价格极端波动风险演化情况出现背离，结合收益率均值来看，贵金属类与农产品类大宗商品期货价格趋于下行，而其他4种大宗商品期货价格趋于上行，走势分化明显。进一步分析可以发现，大宗商品期货价格波动情况两阶段的划分与供给侧结构性改革政策出台的时间(2015年11月)较为一致，且价格趋于上行的工业类、能化类、金属类大宗商品期货，均属于供给侧结构性改革中去产能去库存重点关注的领域。表中ZH、GY、NH、JS、GJS、NCP分别代表综合类、工业类、能化类、金属类、贵金属类、农产品类大宗商品期货。

图1 基于最优测度模型的6种大宗商品极端风险走势图

(六)供给侧结构性改革政策对大宗商品期货价格极端波动风险的影响分析

为更科学评价中国供给侧结构性改革政策是否会影响大宗商品期货价格极端波动风险，本文采用在1%置信水平上的极端多头VaR以及基于FIAPARCH模型获得的条件标准差作为波动率；本文以供给侧结构性改革政策正式出台时间(2015年11月10日)为界，采取虚拟变量XU来代表供给侧结构性改革政策(2015年11月10日之前日期赋0，之后日期赋1)；采取QU代表时间趋势变量(2015年11月11日赋1，之后日期顺次加1)，以检测各种大宗商品期货价格极端波动风险是否在供给侧结构性改革启动后具有明显的时间趋势；与此同时，增加各种大宗商品期货每日收益率r作为自变量，以衡量其每日收益变化是否会对极端风险产生影响，最终估计结果见表7、表8。

表7 供给侧改革政策对各种大宗商品期货价格极端VaR的影响结果表

注：表中数据为估计系数；*、**、***分别表示在10%、5%、1%的显著性水平下显著，下表同。

表8 供给侧改革政策对各种大宗商品期货价格波动率的影响结果表

表7回归结果显示，对整个大宗商品期货市场而言，代表供给侧结构性改革政策的虚拟变量及其时间趋势变量均在1%的置信水平上显著为正，这说明供给侧结构性改革政策在一定程度上加剧了中国大宗商品期货市场价格波动极端风险水平，且随着该政策的推进，大宗商品期货市场风险具有随时间趋于增强的趋势；与此类似，工业类、金属类、农产品类的大宗商品期货极端风险值均受到供给侧结构性改革政策的显著影响，具有明显的时间趋势；但供给侧结构性改革政策对贵金属大宗商品期货价格极端波动风险的影响较弱。

在波动率方面，由表8可知：供给侧结构性改革政策的推出明显加大了整个大宗商品期货市场、工业类、能化类、金属类和农产品类大宗商品期货的价格波动率，其中影响最大的是金属类大宗商品期货，而影响较小的是能化类大宗商品期货。与此相反，该政策的推出对贵金属类大宗商品期货的价格波动具有显著的负面影响，也即明显抑制了该类商品期货的价格波动程度；与此同时，供给侧结构性改革政策在各种大宗商品期货价格波动率的时间趋势上均不太明显。基于实证结果可知，供给侧结构性改革中去产能、去库存的主要措施(如规定去产能目标任务、限制生产时间等)在一定程度上明显加大了中国大宗商品价格波动的极端风险。具体而言，其影响路径可能如下：一方面，去产能、去库存直接导致相关行业产量下降，产能从过剩趋于合理，供给量趋于下降，在这一过程中下游行业对大宗商品未来价格走势的预期可能会拉动其期、现货价格的上涨，供应压力可能会成为影响市场价格走势的主导因素；另一方面，产能收紧及库存收缩将使相关行业供应缺乏弹性，在面对下游行业季节性补库存及其他市场突发情况时，难以通过减少库存减轻价格效应，使得相关大宗商品价格易于产生极端波动。

(七)各种大宗商品期货对外部消息的冲击响应特征分析

图2、图3报告了各种大宗商品期货极端多、空头VaR的消息冲击曲线。从中可以看出：综合类、贵金属类及农产品类大宗商品期货市场对外部利好、利空消息的反应程度一样，具有明显的对称性；工业类大宗商品期货市场的极端多、空头风险受到前一期VaR值的显著正向影响，对外部利空消息的反应程度大于对利好消息的反应程度，具有明显的非对称性；能化类大宗商品期货市场极端多头风险受前一期VaR值影响不明显，而极端空头风险则受到前一期VaR值的显著正向影响，对外部利空和利好消息冲击表现出非对称性；金属类大宗商品期货市场极端多头风险受到前一期VaR值的显著正向影响，但极端空头风险受前一期VaR值影响不明显，同样具有对外部利好利空消息冲击的非对称性响应特征。

图3 各种大宗商品期货极端空头风险的消息冲击曲线图

五、结论与建议

本文将CAViaR处理普通分位数与EVT处理极端风险的优越性结合起来，构建了CAViaR-EVT模型来测度中国大宗商品期货(综合类、工业类、能化类、金属类、贵金属类、农产品类)在2012年9月至2017年9月期间的价格极端波动风险及其市场风险演化模式，并评价供给侧结构性改革政策的推出对大宗商品期货价格波动风险及其波动率的影响，最终研究结果表明：第一，相比传统ARMA-GARCH族-EVT模型，CAViaR-EVT模型更适合测度中国大宗商品期货价格极端波动风险，具有更高的精度和稳健性；第二，各种大宗商品期货市场极端风险适合不同的CAViaR-EVT模型刻画。综合类、农产品类大宗商品价格极端波动风险的最优预测模型为SAV-EVT，工业类、能化类、金属类大宗商品价格极端波动风险的最优预测模型为AD-EVT，贵金属类大宗商品价格极端波动风险的最优预测模型为IG-EVT；第三，供给侧结构性改革政策对中国大宗商品期货市场价格极端波动风险及其走势具有显著正向影响。该政策推出后，工业类、金属类、农产品类大宗商品极端风险值出现频率及程度均有增强趋势，供给侧结构性改革中去库存、去杠杆的主要措施可能通过影响相关大宗商品供给弹性及下游行业预期，进而加剧了大宗商品价格波动的极端风险；第四，各种大宗商品期货市场风险演化模型存在明显差异。整个大宗商品期货市场风险对外部利好、利空消息的反应程度一样，具有明显的对称性，且市场风险具有自我增强趋势。从具体种类看：贵金属类和农产品类大宗商品期货具有对外部利好利空消息冲击的对称性响应特征；工业类大宗商品期货市场的极端多、空头风险受到前一期VaR值的显著正向影响，对外部利空消息的反应程度大于对利好消息的反应程度，具有明显的非对称性；能化类大宗商品期货市场极端多头风险受前一期VaR值影响不明显，而极端空头风险则受到前一期VaR值的显著正向影响，对外部利空和利好消息冲击表现出非对称性；金属类大宗商品期货市场极端多头风险受到前一期VaR值的显著正向影响，但极端空头风险受受前一期VaR值影响不明显，同样具有对外部利好利空消息冲击的非对称性响应特征。

基于上述研究结论，本文提出如下政策建议：一方面，监管部门、金融机构及大宗商品期货投资者可以根据不同大宗商品期货品种所适用的最优极端风险预测模型对大宗商品价格波动风险进行预测，掌握大宗商品期货市场风险演化模式及其对外部利好利空消息冲击的对称或非对称特征来进行风险防范，从而做出及时有效的监管或投资决策；另一方面，鉴于供给侧结构性改革的长期性、复杂性及其对大宗商品价格极端波动风险可能产生的影响，监管层在制定供给侧结构性改革持续推进的相关政策时，有必要及时关注所推出政策对大宗商品期货价格极端波动风险的影响，根据影响结果进一步科学评估和优化相关改革政策，从而在合理平衡供给侧结构性改革的速度与质量的同时防范大宗商品期货市场极端风险的频繁发生。从实践看，供给侧结构改革使得大多数大宗商品供给减少，价格波动上涨，并通过产业链上游向下游传递，在加大上游企业定价权和利润空间的同时也在一定程度上明显削弱了中下游企业的盈利能力。因此，在当前持续深入推进供给侧结构性改革的同时，也要关注上游价格极端波动风险对产业链中下游企业的运营成本及盈利能力所造成的负面影响，必要时应该实施大宗商品的价格指引甚至管制，并抑制大宗商品期货市场的投机行为，缓解其对大宗商品现货价格水平的冲击和非合理引领作用。