利用通道间插值的彩色图像可逆数据隐藏
2018-11-14葛昊立王建军
葛昊立,陈 妍,王建军
(复旦大学 信息科学与工程学院 图像与智能信息处理实验室,上海 200433)
可逆数据隐藏(Reversible Data Hiding, RDH)是一种将信息隐秘地嵌入到对失真零容忍的数字掩体(如图像、视频、音频)中的技术.该技术保证提取嵌入信息的同时能够完全无误地恢复原始数字掩体,我们将嵌入信息后的数字掩体称为隐秘图像.例如,在军事和医疗领域,数字图像的失真是不可接受的所以研究可逆数据隐藏技术来保证原始掩体和嵌入信息的无失真地恢复是信息安全研究领域的一个重要分支.本文研究以图像为掩体的RDH方法.
在早期以数字图像为掩体的RDH文献中,人们使用取模运算[1]和无损压缩[2-3]设计了RDH算法来对图像进行脆弱认证.以数字图像为掩体的RDH方法主要有两种: 差值扩展[4]和直方图平移[5-6].差值扩展的方法对掩体图像进行整数小波变换以产生差值,这些差值会被扩展以预留出额外空间进行信息嵌入.直方图平移的方法通过生成图像直方图并平移直方图的箱格以完成信息嵌入.
随着对RDH的深入研究,人们对上述方法进行了改进,以便提高嵌入容量和隐秘图像的视觉质量.例如,预测误差扩展方法[7-8]考虑了邻域像素间的局部相关性.块直方图平移方法[9]则应用于图像中不重合的块,而不是整幅图像[5].通过使用差值图像的直方图平移,Lee等[10]提出了具有高嵌入容量的RDH方法.另外,人们还提出了这两种方法的组合法[11-14],这些方法分析了特定算法生成的直方图的特性并且选择最优的箱格来进行直方图平移.除了上述的两种主要方法,矢量量化的方法也应用于RDH领域[15].例如,人们提出边匹配的矢量量化方法[16-17]来提高预测的准确性,进而提高RDH算法的性能.
上述的这些可逆数据隐藏算法都是以灰度图像为掩体.然而,实际生活中,彩色图像更加常见,人们也对以彩色图像为掩体的RDH算法进行了研究.例如,Wu等[18]针对加密调色板图像设计了可分离式RDH算法.改进的边匹配矢量量化方法[19]使用参考颜色通道来提高预测的准确性以提高RDH算法的性能.但该算法应用于彩色图像之后得到的是一串码流,而不是和原图像相近的隐秘图像.其他彩色图像上的RDH算法[20-22]则直接由灰度图像中的RDH算法拓展得到.
Luo将插值技术应用在可逆数据隐藏领域[23].该算法利用部分像素对剩余像素进行插值预测,利用预测像素和原像素的误差值以嵌入隐秘信息.Lu[24]将双线性插值和差值扩展相结合提出了一种RDH算法.Govind[25]通过使用方向插值[26]和差值扩展进一步提高了嵌入容量.Yang[22]提出了使用计算块内像素差值和差值图像直方图平移的算法来实现信息嵌入.该方法在真彩色图像的3个通道上实现了可逆数据隐藏,但该文没有探讨通道间的相关性.
基于彩色图像的3个通道间的相关性,本文提出了一种通道间插值的彩色图像可逆数据隐藏算法.该算法用部分像素预测剩余像素,计算预测图像和原始图像的误差,通过修改这些误差可以嵌入秘密信息,实现可逆数据隐藏.为了选取彩色图像的最优插值通道,我们采用以下两种评价指标: 一是插值通道图像和原通道图像之间的峰值信噪比;二是两者间误差图像直方图中最高两个峰值之和.我们选择两种评价指标中的任意一个作为判断标准,对其值最大的通道优先进行嵌入.实验结果表明: 本文提出的方法与现有的方法相比具有更高的嵌入容量和峰值信噪比.
1 通道间插值的RDH算法
本文提出方法的框架如图1所示.该方法的主要思想是: (1) 数据隐藏者将未压缩图像的直方图进行收缩以避免可能的下溢或者上溢;(2) 选择采样像素,对收缩后的图像进行降采样,而没有被选中的像素,本文将其称为非采样像素;(3) 使用通道间插值按顺序对采样像素和非采样像素嵌入位置映射和秘密;(4) 在接收端,借助隐秘图像中的隐藏信息,接收者不仅可以提取嵌入的秘密信息,而且可以准确无误地恢复原彩色图像.下面对提出的算法进行详细叙述.
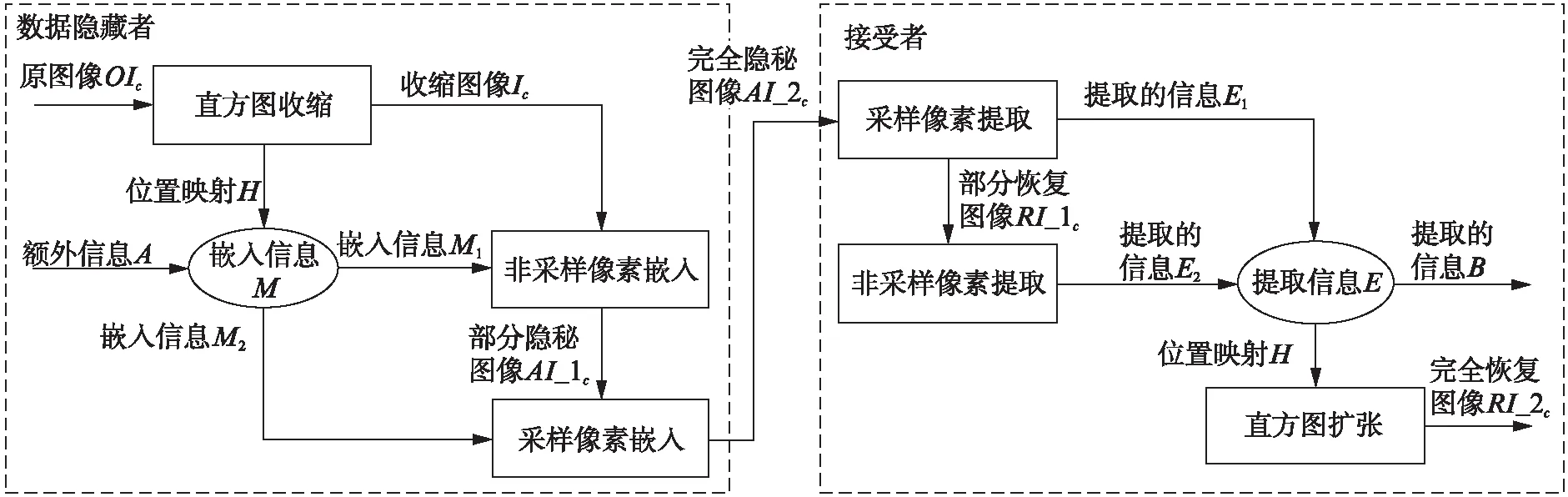
图1 算法框图Fig.1 Scheme of the algorithm
1.1 直方图收缩
本文的可逆数据隐藏算法是以彩色图像为掩体,我们将掩体图像的每一个通道用OIc表示,其中c∈{R,G,B},R、G、B分别表示红、绿和蓝色通道.我们的算法对3个通道进行相同的运算,即从左到右、从上到下的顺序遍历掩体图像中每个通道的每个像素,并根据式(1)
(1)
修改像素值.同时,算法记录一个位置映射H,用以区分原始值为1或254的像素和那些值被修改成1或254的像素.初始化位置映射H为空集合,如果一个像素OIc(i,j)∈{1,254},在H的末端添加一个1;如果OIc(i,j)∈{0,255},则添加一个0.这样可以得到收缩后的图像Ic和位置映射H.然后,H和秘密信息A(一个熵为1的二进制序列)串接得到嵌入信息M,即M=H+A.由于分别在非采样像素和采样像素上进行双层的数据嵌入,M也被分成两份:M1和M2.将M1嵌入到非采样像素中,M2嵌入到采样像素中.这里,M1的长度等于能够在非采样像素上嵌入的比特位数,M2的长度等于能够在采样像素上嵌入的比特位数.
1.2 非采样像素嵌入
首先,通过选取奇数行奇数列(偶数行奇数列等类似的模式也是可行的)的像素对收缩图像进行隔像素降采样.我们定义这些像素为采样像素,如图2中黑色圆圈所示.而图像中的其他像素则被定义为非采样像素,如图2中白色或者灰色圆圈所示.这里按图像长和宽的1/2进行隔像素降采样.这种采样方式可以保证对像素进行插值时总是使用如图2所示的X形或者十字形的模式,从而保证被插值的像素在4个方向上均有参照的邻域像素.这样充分利用了像素的空间相关性,最终提高插值的准确性和嵌入容量.此外,本文的算法具有旋转不变性,不受图像旋转的影响.然后,在45°、135°方向上利用邻域内4个采样像素对一部分非采样像素进行插值,再在0°、90°方向上利用邻域内2个采样像素和2个已插值的非采样像素对剩下的非采样像素进行插值,最终得到基于降采样图像的非采样层的插值图像IPc,具体过程如图2所示.

图2 非采样像素插值Fig.2 Non-sample pixel interpolation
对于边界上的像素,可以使用简单的线性插值或者对边界像素的邻域以镜像复制的方式扩充,以提高插值准确性,具体的插值算法见1.4节.得到插值图像后,计算原通道收缩图像Ic和IPc在非采样像素位置上的差:
DIc(i,j)=Ic(i,j)-IPc(i,j)imod 2≠1 orjmod 2≠1.
(2)
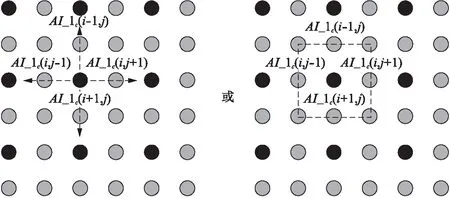
计算误差图像DIc的直方图(我们仅统计非采样像素的直方图),选取该直方图最高和次高的两个峰值点,记录两个峰值对应的分组(bin)为pc,l和pc,h,其中pc,l (3) 其中m是M的第一部分M1中提取出来的一位.虽然直方图平移的时候,直接操作的是误差图像DIc,我们从式(2)得到Ic(i,j)=DIc(i,j)+IPc(i,j),其中imod 2≠1或jmod 2≠1,并且插值图像IPc在直方图平移过程中并没有改变,所以对误差图像DIc直方图的左移或者右移和对Ic直方图的左移或者右移是完全等价的.这样通过式(3),可以得到包含一部分嵌入信息的中间隐秘图像AI_1c. 上面对非采样像素的嵌入进行了叙述,现在讨论中间隐秘图像AI_1c中采样像素的嵌入问题.如图3所示,采样像素依然用黑色圆圈表示,包含隐秘信息的非采样像素现在用灰色圆圈表示. 图3 采样像素插值Fig.3 Sample pixel interpolation 具体插值时,使用采样像素周围4邻域或者8邻域的像素进行估计,得到对应的插值图像RPc.4邻域估计不考虑两个对角线方向的邻域像素(这4个像素由距离中心像素更远的像素估计得到),去除了较远处像素的影响.8邻域估计则将较远处的像素考虑在内,但在估计时通过色度的筛选只考虑合适的像素.这两种不同的邻域估计得到的实验效果十分接近,8邻域估计的效果略好,具体实验结果见2.2节.采样像素的嵌入算法类似于非采样像素,具体过程如下. 计算AI_1c和RPc在采样像素位置上的差: DRc(i,j)=AI_1c(i,j)-RPc(i,j)imod 2=1 andjmod 2=1. (4) 统计采样像素误差图像DRc的直方图并进行误差直方图平移.最终的隐秘图像AI_2c可以通过下式计算得到: (5) 其中:m是M的第二部分M2中提取出来的一位;qc,l和qc,h是误差图像DRc在采样像素位置直方图中最高和次高峰值点对应的分组.对qc,l和qc,h的保存方法同pc,l和pc,h类似. 本节首先分析彩色图像的成像机制,然后利用这个成像机制推导出通道间插值算法,最后,利用通道间插值算法和任意两个颜色通道对第3个颜色通道进行插值和可逆数据隐藏. 假定彩色图像中拍摄的物体表面具有朗伯漫反射的特性,则在物体表面的彩色图像成像可以表示为: (6) 其中:Ik(x)是相机颜色传感器在像素位置x处的输出响应其中k∈{1,2,3},表示对应于RGB3种颜色的传感器;Rf(x,λ)代表物体表面在像素位置x处对波长为λ(单位: nm)的光的反射响应;Sk(λ)表示第k个传感器对于波长为λ的光的响应特性;L(x,λ)是彩色图像拍摄时的环境光照,波长λ和像素位置x的函数,环境光照可能随像素位置x的变化而变化. 假定传感器响应特性可以使用δ函数来表示,那么Sk(λ)=δ(λ-λk),进而可以将式(6)简化得到: (7) 我们不关心λk具体的数值为多少,只关心其对应的颜色通道编号,所以可以将λk省略并且把k移到下标位置.简而言之,即Ik(x)=Rfk(x)Lk(x),其中k=1,2,3.将该式写成RGB3个颜色通道,即将像素的值用物体表面响应和环境光照的乘积在长、中和短波个3波段上的分量表示: (8) 将环境光照向量L(x)=(L1(x),L2(x),L3(x))表示成光照强度‖L(x)‖乘以光照色度α(x)(也是光照方向): L(x)=‖L(x)‖α(x), (9) (10) 假定物体表面反射Rfk(x)和光照色度α(x)具有局部连续一致性.更准确的讲,对图像上的任意一个像素,在其邻域范围内总存在另一个像素,其物体表面反射和光照色度与该像素相同.比如,对两个相邻的像素x1和x2,如果Rfk(x1)=Rfk(x2),α(x1)=α(x2),那么像素x1的色度就和其邻域像素x2的色度相等,即r(x1)=r(x2),g(x1)=g(x2),b(x1)=b(x2). 从以上的相机成像机制和推导出发,本文提出了通道间插值的算法来进行可逆数据隐藏.我们以R通道和B通道对G通道插值为例来说明插值过程,如图4所示. 图4 通道间插值Fig.4 Inter-channel interpolation (11) (12) 图5 边缘处插值Fig.5 Interpolation on the edge 这里像素估计算法没有直接对邻域内所有像素取加权平均,而是对邻域像素进行筛选,剔除掉与中心像素色度相差较大的像素,以减小估计误差.例如,数字图像中,边缘通常出现在物体表面分界处和阴影处,而这些边缘两侧的像素色度一般相差较大,如图5所示.假设图像中某条边缘如红线所示,中心像素与右上角的像素位于边缘的同一侧,它与G2的颜色相近,而中心像素与像素G1、G2、G4位于边缘的两侧,它们的颜色相差较大.就可以排除其他3个像素G1、G2、G4的干扰,提高插值的准确性. 图6 嵌入与提取顺序Fig.6 Sequence of embedding and extraction 为了提取出嵌入信息并且恢复原图像,需要按顺序在采样像素位置和非采样像素位置进行信息提取.这个顺序刚好和嵌入过程完全相反.假设嵌入的时候按照RGB的顺序嵌入信息,则相应的嵌入和提取顺序如图6所示.其中R1表示红色通道非采样像素的集合,R2表示红色通道采样像素的集合,R1′代表嵌入信息之后的R1像素集,R2′代表嵌入信息之后的R2像素集.蓝色和绿色通道也是类似. 在信息提取过程中,分别根据非采样像素和采样像素使用同样的插值算法产生对应的插值图像并计算相应的误差图像.以对采样像素集B2进行嵌入和提取为例,嵌入时使用G2′、R2′、R1′、G1′、B1′对其进行通道间插值,而提取时也是使用完全相同的参考像素集进行相同的通道间插值.这样,根据图6所示的和嵌入顺序完全相反的提取顺序,本文算法可以保证其可逆性. 根据自包含在图像每个通道前两行的4个峰值pc,l、pc,h(对应于非采样像素集)以及qc,l、qc,h(对应于采样像素集),通过反向平移误差图像的直方图(和嵌入时误差图像直方图的平移方向恰好相反)可以提取出嵌入信息.在采样像素上进行信息提取,恢复采样像素的公式如下: (13) 其中DRc(i,j)是采样像素上的误差图像.恢复原采样像素的同时,按照下式提取信息: (14) 类似地,用DIc(i,j)表示非采样像素上的误差图像,则非采样像素的恢复和信息提取如公式(15)和(16)所示. (15) (16) 由于嵌入时采用了最低有效位替换的方法将pc,l、pc,h、qc,l和qc,h保存在每个通道的前两行,所以还需要将图像每个通道的这两行重新替换回原始值,以保证算法的可逆性. 最终,需要根据提取出信息中的位置映射进行直方图扩张以恢复原先的纯黑像素(像素值为0)和纯白像素(像素值为255),即: (17) 本文可逆数据隐藏算法的性能和插值准确性密切相关.像素插值估计越精确,嵌入容量越高,峰值信噪比也越高.因此,本部分先实验验证通道间插值算法的准确性,然后将本文的通道间插值可逆数据隐藏算法和现有的算法进行比较. 为了说明通道间插值算法的性能,本文使用了两种评价指标.这两种指标都可以表征插值图像和原图像之间的相似程度.一种是插值通道图像和原通道图像之间的峰值信噪比(Peak Signal-to-Noise Ratio, PSNR),另一种是两者间误差图像直方图中最高两个峰值之和,该指标表征了每个像素变化不超过1的情况下嵌入容量的大小. 实验中,随机选取UCID数据集[27]中的10幅图像,进行通道间插值,使用上述两种指标比较插值图像和原图像的相似程度,并重复10次.和本文插值算法进行比较的方法有Luo[23]和Zhou[28].Luo最早在可逆数据隐藏领域使用插值算法,其使用的插值算法是方向插值;根据Yu[29]的评估,Zhou的插值算法和双线性插值、双三次插值及其他3种插值算法[26,30-31]相比是最好的.这里显示了其中20幅图像在两种评价指标下的比较结果. 表1呈现了这20幅插值图像PSNR比较的结果. 表1 峰值信噪比比较Tab.1 Comparison of PSNR 注: 1)数字为图像编号. 表2呈现了误差图像最高双峰之和比较的结果. 表2 双峰之和比较 (续表) 注: 1)数字为图像编号. 由表1和表2可以看出,在两种评价指标下,本文的插值算法都是最好的.一般而言,PSNR值越高,误差图像直方图在分组0附近越尖锐.那么,在进行多次直方图平移的时候,就可以获得更高的嵌入容量.其中,嵌入容量(Embedding Capacity, EC)用嵌入的比特位数除以图像的像素数来表示,单位为bpp(bit per pixel).第二个评价指标误差图像最高双峰之和体现了单次直方图平移(这样每个像素变化不会超过1)下的嵌入容量.因此,当需要进行多次嵌入的时候,选用PSNR指标进行评判以选取优先嵌入通道;当嵌入信息较短时,使用第二个指标进行评判. 为了验证本文提出的通道间插值可逆数据隐藏算法的性能,本文在4幅标准测试图像上进行实验.这4幅图像均来自USC-SIPI数据集[32],大小均为512×512.它们被广泛地应用于可逆数据隐藏研究中,如图7所示.为了在彩色图像上实现可逆数据隐藏,需要根据3.1节提出的评判标准选取嵌入信息的通道顺序.指标高的通道优先进行嵌入,指标最低的通道需要使用其他两个包含嵌入信息的通道进行通道间插值并嵌入,这样才能保证整体算法的可逆性.当然,表征嵌入顺序的比特位也要嵌入到图像中.由于只有3个通道,全排列只有6种情况,所以只需要3个比特位即可表示嵌入顺序. 图7 标准测试图像Fig.7 Standard test images 1.3节说明了对采样像素估计时可以使用4邻域或者8邻域.表3显示了针对4幅标准图像绿色通道进行本文算法在这两种不同估计方式下的实验结果. 表3 4幅标准测试图像在4邻域和8邻域下EC、PSNR和运行时间比较 表3中的数据在MATLAB R2015b和8GB内存的实验环境下测得.由表3可以看出8邻域的PSNR和EC均略高于4邻域,而运行时间则稍多于4邻域.因此,本文算法对采样像素的估计采用了8邻域的估计方式. 本文算法与Luo[23]、Lu[24]、Govind[25]和Yang[22]算法进行了比较.具体的EC和PSNR如表4所示. 表4 4幅标准测试图像EC与PSNR比较 表4中Lu算法和Govind算法在有些情况下的嵌入容量是负的,也就是说不能嵌入任何信息.这是由于Sailboat图像绿色通道中有较多的0值,进而导致较长的位置映射,而该通道可嵌入的比特数小于位置映射的长度,从而出现负的嵌入容量.图8还画出了4幅图像绿色通道的PSNR-EC曲线. 图8 4幅标准测试图像PSNR-EC曲线Fig.8 PSNR-EC curve of four standard test images 从表4和图7均可以看出,相同嵌入容量下,本文算法具有更高的PSNR;而不限制PSNR的情况下也拥有更高的嵌入容量. 尽管上面4幅图都是优先使用R和B通道对G通道进行插值嵌入,然而并不是所有图像都是这样.本文在UCID数据集[27]的1338幅彩色图像上进行了实验,将本文提出算法与Luo[23]提出的算法所得数据进行了比较,我们发现本文算法在67幅图像上嵌入性能和Luo[23]算法相当.在剩余的1271幅图像上嵌入容量和PSNR均有提升,其中362幅图像优先对R通道插值嵌入,463幅图像优先对G通道插值嵌入,446幅图像优先对B通道插值嵌入.这说明不同图像优先嵌入通道并不固定,需要根据图像自身内容自适应地选取. 由于3个彩色通道具有高度相关性,本文探讨了利用这种相关性来对图像通道进行插值,并提出了一种通道间插值的策略来产生精准的插值图像.基于彩色图像成像过程中朗伯反射和一些局部不变特性的假设,本文验证了当像素强度消除时,局部色度具有相似性.利用这种局部色度一致性,本文提出了一种彩色图像可逆数据隐藏方法,并通过大量实验,验证了本文提出算法的性能.实验结果表明,相比于现有算法,本文算法可以获得更高的嵌入容量和峰值信噪比.1.3 采样像素嵌入
1.4 通道间插值
α(x)=(α1(x),α2(x),α3(x)).

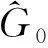


1.5 信息提取与图像恢复

2 结果与讨论
2.1 插值算法性能



2.2 可逆数据隐藏算法性能




3 结 论
