多资产挂钩的结构性理财产品定价研究

方 艳，张元玺，刘津智，张 洁

(1.上海对外经贸大学 金融管理学院，上海 201620； 2.上海财经大学 统计与管理学院，上海 200433； 3.长春信息技术职业学院 基础教学部，长春 130012)

2015年6月以来，我国股票市场大幅下跌.为了应对持续低迷的股市和不断下降的利率，投资者开始将“保本”设为理财的首要目标，并开始寻求一种在市场价格下跌时保证本金而上涨时确保收益的产品，这毫无疑问地给结构性理财产品(Structured Product)的发展带来了新契机.简单地说，结构性理财产品就是债券加期权，即发行人根据投资者的不同风险偏好、利用金融工程技术将债券和期权相结合的一种衍生产品，其中，债券是为了确保本金，而期权是为了获取收益.与投资资产管理计划相比，结构性理财产品的最大优点在于其投资门槛较低.因此，在股市低迷和利率走低的大环境下，结构性理财产品的出现吸引了越来越多投资者的关注.然而，相对于一般的理财产品来说，结构性理财产品更为复杂.

在国内，一方面，产品发行者不仅缺乏金融衍生产品的设计能力和国际投资经验，还忽视对结构性理财产品设计和定价方面人才的开发和培养，从而导致国内资产管理机构在结构性衍生产品领域不仅不能独立完成产品的设计、推广和销售，还需要借助外资银行的衍生品交易经验对产品中的期权进行套期保值；另一方面，普通投资者对这类产品更是缺乏理性、全面地认知和理解，因此，他们对其常抱着两种极端的态度： 敬而远之或非理性盲从.

总之，从发行者的角度来讲，掌握结构性理财产品的设计和定价方法、制定出满足市场需求的理财产品、摆脱对外资金融机构的依赖是国内金融机构扩展市场份额、增强市场竞争力和盈利能力、开拓新的利润增长点等方面的重要举措.从投资者的角度来讲，让投资者更好地认识结构性理财产品，了解结构性理财产品的定价原理、风险和收益特征，合理预期结构性理财产品的投资，这不仅是理性投资的关键，也是关系到我国投融资市场的理性运作、规范建设、健康发展等方面的问题.

因此，透彻深入地分析金融产品背后创新的过程、从产品发行者角度来对已有结构性理财产品的设计和定价进行创新和改进，这既为银行在竞争激烈的市场中脱颖而出提供有力的支撑，又为投资者对未来理财产品的选择提供有效的信息.然而，怎样合理地对结构性理财产品进行定价、有效地平衡发行者和投资者间的利益以及充分地对冲和管理各种风险，这些都是值得研究的话题.为此，本文将对结构性理财产品进行分析与探讨，这不但为产品设计者在产品设计、产品定价等方面提供一定参考，还为个人投资者选择理财产品提供一定的投资建议.

1 文献综述

现代意义上的结构性理财产品于20世纪70，80年代始于美国，并于90年代出现爆炸式增长.伴随着产品的兴起，各国学者对结构性理财产品也相应地进行了大量研究，且研究的焦点主要集中于产品定价问题上.由于结构性理财产品大多是固定收益证券与期权等金融衍生品的结合，因此，产品定价的关键在于期权等衍生品的定价.

关于期权定价，早在1973年Black等创立BS(Black-Scholes)期权定价模型[1]，随后Cox等[2]于1979年创立了期权定价的二项式方法.其中，BS模型为当今结构性理财产品的发展奠定了基石.随着期权定价理论的发展，结构性产品定价也不断完善发展.1990年，Chen和Sears[3]对SPIN(Standard and Poor’s 500 Indexed Note)产品进行了研究，提出了SPIN定价模式；Chen和Wu[4]等对瑞士银行等发行的结构性理财产品进行研究；Deng等[5]运用蒙特卡罗模拟、数值积分、分解法和偏微分方程4种方法进行了结构性理财产品的定价研究.其他参考文献有Benet等[6]，Bernard和Boyle[7]，Wallmeier和Diethelm[8]，Entrop等[9].

虽然我国的结构性理财产品市场起步较晚，但国内学者对其也进行了大量深入的研究.如，康朝锋和郑振龙[10]用BDT(Black-Derman-Toy)模型对2004年初发行的外汇结构性存款进行定价；任敏和陈金龙[11]根据风险中性定价原理，借鉴BS期权定价方法，对受汇率波动影响的外汇理财产品进行定价研究；孙兆学[12]利用黄金价格在不同时期的涨跌程度，研究一款与黄金挂钩的结构性理财产品；崔海蓉等[13]基于行为金融学相关理论研究了具有嵌入式障碍期权的结构化产品的设计和定价问题.但是，目前国内针对多资产挂钩的结构性理财产品定价研究的文献还较少.相应的文献如： 陈金龙和任敏[14]、崔海蓉等[15]、Chen和Peng[16].通过对这些已有的文献进行分析，可以发现目前关于多资产挂钩的结构性理财产品定价分析基本上都是采用Cholesky分解方法解决多资产间的相关性问题.然而，该分解方法的最大缺陷是不能充分、有效地刻画挂钩资产间的尾部相关性(Correlation Coefficient)或相依性(Association)，进而导致定价结果的误差偏大.为了精确刻画资产间的尾部相依性，目前已有学者开始采用Copula函数(Sklar[17])来拟合变量间的尾部相依性.譬如，Hu[18]利用混合Copula函数分析不同市场指数间的尾部相依性；Cai和Wang[19]用混合Copula函数分析股票市场的联动性；方艳等[20]用Copula函数研究分析沪港通的开启对香港和内地股票市场间联动性的影响.但是，目前国内鲜有文献涉及将Copula函数尤其是混合Copula函数与多资产挂钩的结构性理财产品的定价问题相结合.为此，本文将混合Copula函数运用于多资产挂钩的结构性理财产品定价中，从而进一步丰富我国的产品定价模型.

本文首先借助混合Copula函数对资产间尾部相依性进行拟合；然后利用蒙特卡罗模拟(Monte Carlo simulation)方法对多资产挂钩的结构性理财产品进行合理定价；最后将其定价结果与现有模型的定价结果进行对比分析并找出一种具有相对优势的定价方法.本文旨在为今后国内金融机构在多资产挂钩结构性理财产品的设计和发行提供思路和建议，为普通投资者正确评估结构化产品以及合理选择结构化产品提供重要参考和依据.

2 多资产挂钩的结构性理财产品定价模型

多资产挂钩的结构性理财产品的定价由两部分构成： 固定收益部分(债券)和浮动收益部分(期权).为此，本文将分别讨论这两部分的定价.

2.1 固定收益部分定价

固定收益部分定价类似于债券的定价,一种广泛被认同的方法是现金流贴现法.根据结构性理财产品的约定，将未来债券可以产生现金流的贴现值来评估该债券的价值，即固定收益部分的价值.现金流贴现公式如下：

(1)

式中：V表示债券价格；B为债券到期偿还的本金；i为债券贴现率，其数值可以根据具体产品来选取；m为一年中债券支付利息的次数；T为债券总年；It为t时期的利息.

2.2 期权部分定价

对于多资产期权的定价，目前已有文献基本上都是采用Cholesky分解法来刻画多资产的相关性问题.然而，Cholesky分解进行蒙特卡罗模拟定价法需遵循正态分布、常数波动率、线性相依性等假定，因而，其本身存在某些系统性缺陷.相对而言，Copula函数借助二分法(即边缘分布和联合分布的单独拟合)的优势，从而准确地捕捉各资产间动态、非对称、非线性的相依结构.为此，本文首先对各期权的边缘分布进行单独拟合，然后通过Copula函数对期权间的尾部相关性进行刻画，最后通过蒙特卡罗模拟方法算出理财产品价格.

2.2.1 EGARCH模型

一般来说，与产品挂钩的标的资产均为时间序列数据，而在金融时间序列研究中，由于GARCH(Generalized Auto-Regressive Conditional Heteroskedasticity)模型(Bollerslev[21])能很好地描述金融时间序列的波动聚类和时变波动特性,因此国内外学者常选用GARCH类模型来描述金融变量的边缘分布.但是在实际市场中，价格下跌比同样程度价格上涨产生更大的波动，即价格收益率的序列不是对称的而是有偏的.为此，Nelson[22]于1991年在GARCH模型的基础上提出了非对称的EGARCH(Exponential GARCH)模型，表达式为：

(2)

式中： 标准收益率vt是均值为0，方差为1的任意分布；φ为冲击系数，即利好消息与利空消息为市场波动带来的杠杆效应未知参数.由于在运用Copula函数建立相依结构时，其边缘分布需满足[0,1]上的均匀分布，为此，本文采用经验分布函数(Empirical Distribution Function)对标准收益率vt的边缘分布进行估计.

2.2.2 Copula函数

随着金融市场的发展，金融资产间的关系变得越来越复杂,且常常呈现出动态非线性、非对称性和尾部相依等特性，因而在处理金融变量间的相关结构时，传统的度量方法尤其是基于线性相关的方法存在较大的局限性且难以刻画这种日趋复杂的相互关系.作为相依关系度量的一种新方法，Copula函数已受到众多学者的青睐，并被广泛地应用于风险管理、资产定价、投资组合等领域.

具体来说，假设随机向量X=(X1,X2，…,Xp)的边缘分布u=Fi(xi)，i=1,2，…,p.根据Sklar定理[17]，随机向量X的联合分布F(x1,x2,…,xp)可分解两部分： 1) 边缘分布F1(x1),F2(x2),…,Fp(xp)；2) 连接边缘分布的相依结构C(·).具体表达式如下：

F(x1,x2,…,xp)=C(F1(x1),F2(x2),…,Fp(xp)),

(3)

式中：F(·)为联合分布函数；C(·)为Copula函数，且C(F1(x1),F2(x2),…,Fp(xp))∈[0,1].Copula函数描述了变量间的相依关系，而边缘分布描述了每个变量各自拥有的属性特征.如果边缘分布函数Fi(xi)是连续的，则Copula函数C(·)是唯一的，否则，Copula函数只在各边缘累积分布函数值域内是唯一确定的.反过来，如果给定Copula函数为C(u1,u2,…,up)，其中ui∈[0,1]，i=1,2，…,p，则存在以下关系：

(4)

相应地，以F1(x1),F2(x2),…,Fk(xk)为边缘分布的联合分布的概率密度函数可表示为：

(5)

式中：fi(xi)为变量i的边缘概率密度函数；c(·)为Copula函数C(·)的密度函数，可表示为：

(6)

Copula函数的二分性充分地提高了模型拟合的灵活性，从而大大地简化了模型的估计问题.目前已存在众多的参数Copula函数表达式，其中，常用表达式有椭圆Copula、阿基米德Copula和极值Copula等(Nelson[22]).关于Copula理论的应用研究，请参考Joe[23]，Genest等[24]，Fang等[25].

2.2.3 混合Copula函数

然而，在现实中，鉴于单一的Copula函数很难充分描述金融变量间全面的相依结构，以及为了更好地拟合多资产收益率同时上涨及同时下跌的相依结构，本文将几个单Copula函数组合进而构成混合Copula函数来分析资产间的相依结构.由m个单Copula函数线性组合而成的混合Copula函数的表达式为：

CMixed(u1,u2,…,up;δ,ω)=ω1C1(u1,u2,…,up;δ1)+ω2C2(u1,u2,…,up;δ2)+…+

ωmCm(u1,u2,…,up;δm),

(7)

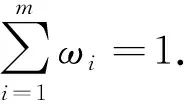
对于混合Copula函数的估计，传统的极大似然估计方法无法剔除本不显著的Copula函数，进而造成模型估计的失真.为此，本文首先利用惩罚函数(Cai和Wang[19])剔除混合Copula函数中不显著的Copula函数，然后再对剩余模型进行估计，这将提高模型对数据的拟合精度和效率.惩罚似然函数的具体形式如下：

(8)

对于相依参数和权重参数的估计，由于混合Copula函数的极大似然函数较复杂，故本文将借助交叉验证法和EM(Expectation-Maximization)算法对优化后的模型进行高效而精确地估计.

在估计出Copula函数各参数之后，本文进行蒙特卡罗模拟定价(Boyle[27]).基于混合Copula函数的资产定价的具体步骤为：

第1步，通过EGARCH模型拟合金融资产收益率的边缘分布；

第2步，将EGARCH模型中得到的标准收益率vt转化为[0,1]上的均匀分布，并代入混合Copula函数进行参数估计；

第3步，在估计出混合Copula函数各参数之后，随机生成一对来自混合Copula分布的随机变量(u,v)；

第4步，将随机变量(u,v)代入其概率分布的反函数，借助各资产的边缘分布得到模拟的资产收益率序列，得到资产收益率一条价格路径；

第5步，将价格路径结合理财产品嵌入期权的支付条款，从而计算最终收益.在风险中性测度下，将此终值按照无风险收益率折现得到期权的价值p(注意： 这个现值p就是期权价值的一个可能情形)；

第6步，重复第3步到第5步N次，模拟获得N个期权价值的可能情形，计算N个样本的均值E[p]，即期权的最终理论价格.

3 实证分析

本文选取固定收益部分为零的“法兴银行——2014年2年期股票指数挂钩人民币结构性理财产品”研究多资产挂钩的结构性理财产品期权部分的定价.

3.1 法兴银行的两股指挂钩人民币理财产品收益结构分析

法兴银行的两股指挂钩人民币理财产品的基本信息： 最低认购金额为100000，保证100%本金安全，风险等级为低风险产品.由于该产品管理费率等数据缺失，为此本文采用同时期发行的相似产品的费率进行替代，其中，销售服务费率为0.5%每年，管理费率为0.3%每年，托管费率为0.05%每年.在剔除一系列费用后，该理财产品的实际价格为98300元.产品挂钩标的为台湾证券交易所加权指数(Taiwan weighted index，TWII)和欧洲斯托克50指数(EURO Stoxx 50 index，STOXX50).产品挂钩标的资产的期初和期末价格分别为期初(2014-04-30)和期末(2016-04-29)该挂钩指数的收盘价格.本产品每半年观察与付息一次，根据挂钩标的客户将获得如下收益： 若全部挂钩标的资产的评价价格均大于或等于其预设水平，投资者可获得相对应的当期收益率；否则，投资者将不能获得任何当期收益率.具体来说，收益信息如表1所示.

表1 产品收益信息表

注意：ri,tj表示第i个资产在第tj期的收益率,其中：i=1,2；j=1,2,3,4.

根据表1可知： 若产品生效日至2014年10月30日区间内台湾加权指数与欧洲斯托克50指数收益率均大于-9.5%，收益为3.50%；若产品生效日至2015年4月30日区间内两指数收益率均大于-4.5%，收益为3.50%；若产品生效日至2015年10月30日区间内两指数收益率均大于0.5%，收益为3.50%；若产品生效日至2016年4月29日区间内两指数收益率均大于5.5%，收益为3.50%；若以上4个条件均满足，则投资者可额外获得3.5%的收益；若以上条件均未满足，则投资者仅获得投资本金.

3.2 产品定价

由于上述的结构性理财产品挂钩标的为台湾加权指数以及欧洲斯托克50指数，故本文未考虑红利在期权定价中的影响.样本为2012年1月1日至2013年12月31日[注]该样本区间的选取是为了匹配产品运行周期，这将极大程度地减小产品设计、产品审批以及资金募集所消耗时间的影响.的台湾加权指数以及欧洲斯托克50指数日收盘价，剔除两指数不同交易日的数据，最终的样本量为485.另外，鉴于产品运行周期为两年，本文选取2014年4月份2年期中国人民币定期存款利率作为期权定价中的无风险利率r.数据源于万德数据库及雅虎金融数据库.

本文采用百分比对数收益率，其计算公式为：

ri,t=100×(ln(Pi,t)-ln(Pi,t-1))，

(9)

式中：ri,t和Pi,t分别为t时刻第i个指数的日对数收益率和日收盘价，i=1,2，且1和2分别对应台湾加权指数和欧洲斯托克50指数.台湾加权指数以及欧洲斯托克50指数日对数收益率的时间序列图如图1所示.

图1 台湾加权指数及欧洲斯托克50指数日对数收益率序列的时序图Fig.1 Time sequence plot for daily log returns of Taiwan weighted index and EURO Stoxx 50 index

图1表明台湾加权指数以及欧洲斯托克50指数存在波动率的群集现象，但是，总体来说，它们都比较平稳.故本文采用EGARCH模型分别对台湾加权指数以及欧洲斯托克50指数的对数收益率进行拟合分析.日对数收益率的描述性统计量如表2所示.

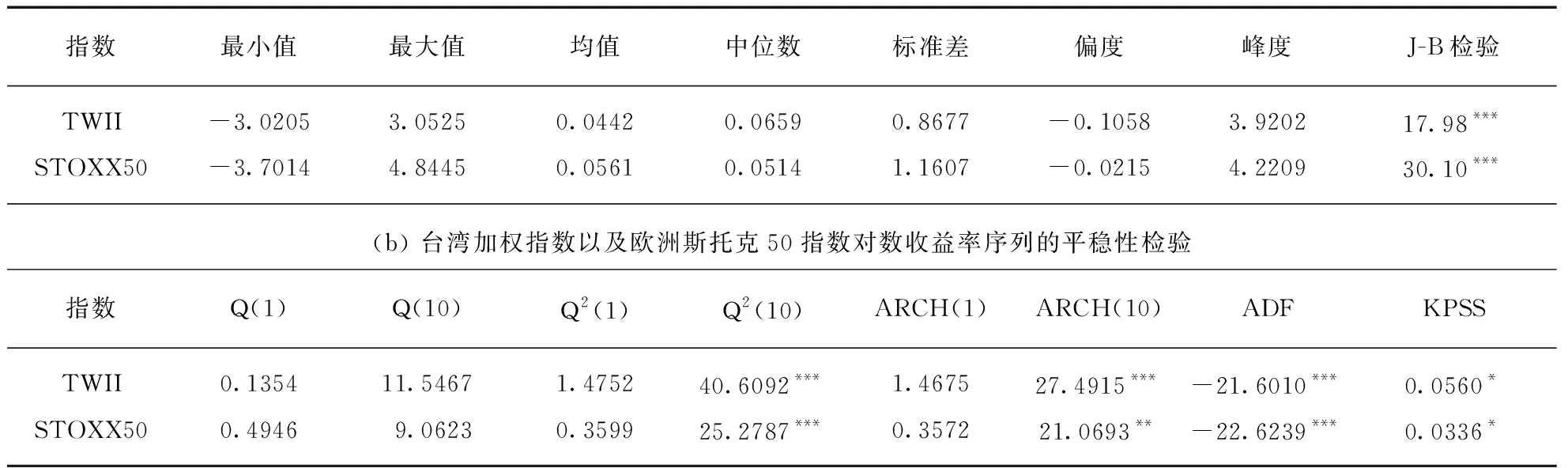
表2 台湾加权指数以及欧洲斯托克50指数日对数收益率序列的统计描述量

注： Jarque和Bera[28](J-B)统计量检验数据分布的正态性；Q(n)和Q2(n)分别表示了检验收益率序列和平方收益率序列n个自相关系数是否同时为0的Ljung和Box[29]统计量；ADF和KPSS分别表示Augmented Dickey and Fuller[30]和Kwiatkowski等[31]，ADF为单位根检验，而KPSS为平稳性检验；*,**和***分别表示10%，5%和1%置信水平.

由表2可知： 台湾加权指数以及欧洲斯托克50指数日对数收益率均值接近于0且对应的标准差都较小，这不仅说明了两对数收益率的波动率较低，还再次验证了该产品的风险等级为低风险产品；对数收益率序列分别存在左偏性质(偏度都为负数)和峰度(峰度值都大于3)，其分布都显著异于正态分布(J-B检验的p值均小于1%)；Ljung和Box统计量Q关于收益率序列自相关性的检验表明收益率序列不存在自相关现象(即均为白噪声序列)，但其平方收益率序列的Q统计量表明两对数收益率存在显著的异方差性；单位根检验结果一致地表明了两指数收益率序列都不存在单位根，而平稳性检验验证了指数收益率的平稳性.简而言之，两市场的日对数收益率均具有明显的尖峰特征、非正态性、非对称性和异方差性.

由于台湾加权指数收益率以及欧洲斯托克50指数收益率均不存在显著的自回归现象，故本文将其设为白噪声序列，即

r1,t=μ1,t+ε1,t；r2,t=μ2,t+ε2,t.

(10)

相应地，本文采用式(2)中的EGARCH(1,1)模型来刻画其波动率.另外，由于市场指数对数收益率显著异于标准正态分布，故本文假定收益率序列来自t分布，并使用惩罚似然函数对模型进行估计,结果如表3所示.

表3 台湾加权指数和欧洲斯托克50指数日对数收益率序列在t分布下的EGARCH(1,1)模型估计及检验结果

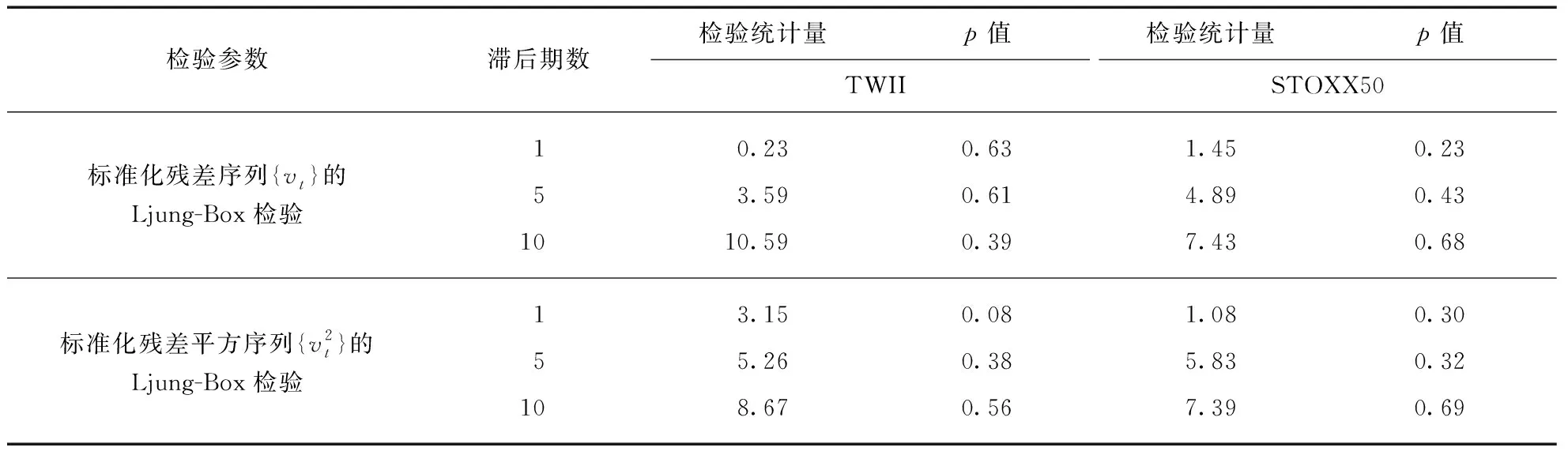
(b) 台湾加权指数和欧洲斯托克50指数日对数收益率序列在t分布下的EGARCH(1,1)模型的检验结果2

注： 括号中数值为参数估计的t值；*,**和***分别表示10%，5%和1%置信水平.

根据表3，我们可以发现： 基于5%的置信水平下，收益率序列t分布的自由度显著不为零，且时间序列的异方差均显著存在.此外，φ的系数均明显为负，这表明利空消息会给两市场带来更大的冲击，从而加剧市场的波动.同时，为了检验t分布的EGARCH(1,1)模型对数据拟合的充分性，表3还提供了模型的标准化残差序列以及标准化残差平方序列的Ljung-Box检验.检验结果表明： 基于5%的置信水平下，不论是标准化残差序列还是标准化残差平方序列都不存在显著的序列自相关性.因此，带t分布的EGARCH(1,1)模型不但能够较好地反映台湾加权指数和欧洲斯托克50指数日对数收益率序列的异方差性,还能较准确地估计其日对数收益率的波动率.

图2分别给出了台湾加权指数和欧洲斯托克50指数的边缘分布均为EGARCH模型时得到的标准化残差及其经验分布的散点图，可以发现其散点图并不服从任意单个Copula函数的分布图，为此，本文将用混合Copula函数来拟合它们间的相依结构.一般来说，Clayton Copula能较好地刻画下尾性,相应地Gumbel Copula将充分地剖析上尾性.

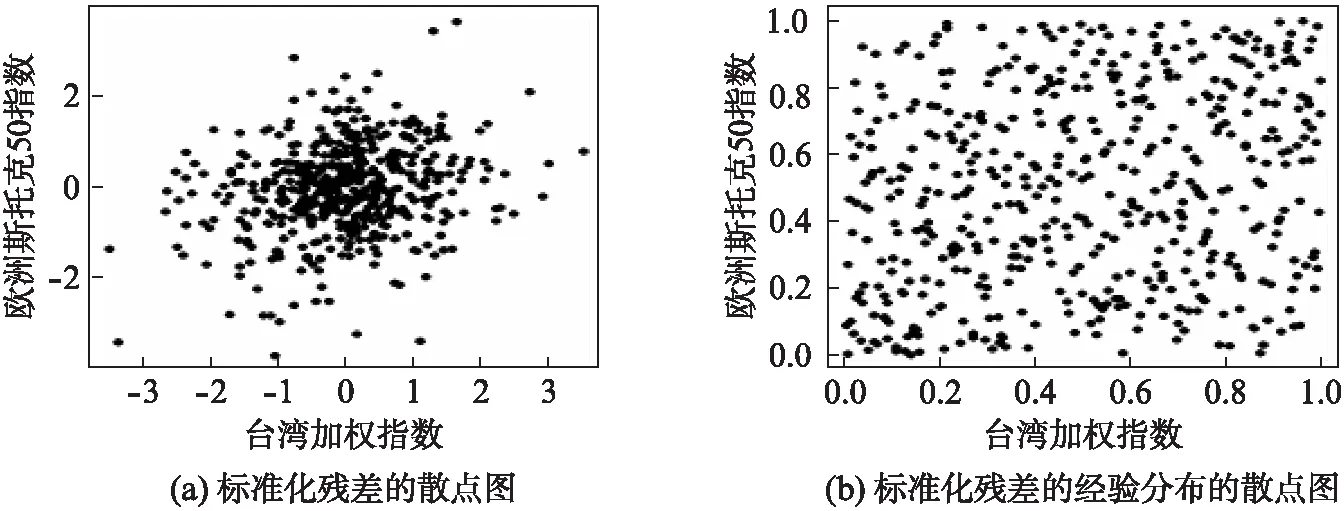
图2 台湾加权指数以及欧洲斯托克50指数的散点图Fig.2 Scatter plots for Taiwan weighted index and EURO Stoxx 50 index

结合图2，本文将借助由Clayton和Gumbel构建的混合Copula函数进行定价分析，其具体表达式为：

CMixed(u,v;δ,ω)=ω1CClayton(u,v;δ1)+(1-ω1)CGumble(u,v;δ2)，

(11)

式中：u和v分别表示台湾加权指数和欧洲斯托克50指数的概率累积函数.Clayton Copula的表达式为：

CClayton(u,v;δ1)=(u-δ1+v-δ1-1)-1/δ1δ1∈[-1,+){0}；

(12)

而Gumbel Copula的表达式为：

CGumble(u,v;δ2)=exp[-{(-lnu)δ2+(-lnv)δ2}1/δ2]δ2∈(1,+).

(13)

对于混合Copula函数的估计，利用交叉验证法得出惩罚函数的光滑参数λ为1.22.通过EM算法与BFGS(Broyden-Fletcher-Goldfarb-Shanno)算法，借助Matlab软件得到各Copula函数的权重及参数估计值见表4.

表4 混合Copula函数估计结果

注： 括号内为标准差.

由表4可知，在5%的置信水平下，权重值ω1，Clayton Copula的参数值δ1和Gumbel Copula的参数值δ2均统计显著不为0.然而，我们可以发现Gumbel Copula参数值的估计接近其取值范围的下界.尽管如此，Gumbel Copula在混合Copula函数中占有相当的一席之地(其权重显著地为0.8827).总之，式(11)定义的混合Copula函数充分地刻画了台湾加权指数和欧洲斯托克50指数的相依性.

根据以上信息，我们确定产品到期收益函数，然后利用蒙特卡罗模拟方法模拟标的资产价格，进而可以求出产品价格.蒙特卡罗模拟法模拟N次，可以产生N条模拟路径，从而获得N个不同的表现水平.图3给出了模拟次数为1000时欧洲斯托克50指数和台湾加权指数的模拟路径.

图3 混合Copula函数下台湾加权指数和欧洲斯托克50指数Fig.3 Simulation results for both Taiwan weighted index and EURO Stoxx 50 index obtained from mixed Copula function

为了说明混合Copula函数在定价中的精确性和合理性，本文分别采用单个Copula函数(包括常用的3个Copula函数，即Clayton，Gumbel和Frank)、混合Copula函数以及Cholesky分解法[注]在Cholesky分解方法进行期权定价中，欧洲斯托克50指数与台湾加权指数对数收益率的相关系数为0.2121.在蒙特卡罗拟次数为500，1000，5000，10000，50000时对期权进行定价，其结果见表5.

表5 Cholesky分解法、单个Copula函数以及混合Copula在不同拟合次数下的期权定价结果

从表5可以发现，Cholesky分解法得到的价格都高于其实际价格且偏差较大、偏误率较高(均超出1%的水平).相应地，不论是单个Copula函数还是混合Copula函数得到的价格都低于其实际价格，即该产品定价是溢价发行，发行价格偏高，损害投资者的利益.另外，我们还发现： 1) 基于Copula函数的定价精度优于Cholesky分解法的定价精度；2) 混合Copula函数比单个Copula函数的定价更为精确，其与真实价格的偏差均为最小，更接近产品的实际发行价格；3) 1000次的蒙特卡罗模拟次数足以确保模拟结果的精确性和可靠性，此时混合Copula函数的定价与期权真实价格的价差约为336元，模型定价偏误率为0.3%.Hu[18]、Cai和Wang[19]的研究均表明混合Copula函数能更充分地刻画多资产间的联动性，故本产品的溢价发行是合理的.此外，溢价发行是金融产品发行的一种价格选择，也是金融产品发行中较为常见的手段.它不仅让发行者获得按票面金额计算的资金，而且还给发行者带来溢价收入，甚至在不增加发行数量的条件下为发行者提供获取更多资金的途径.但是，高溢价发行使投资成本过高、投资回报过低，将促使市场变成一个投机取巧的市场.通过上述分析，可以发现基于混合Copula函数的定价是溢价发行，但不是高溢价发行.因此，其定价是合理、可信的.

最后，本文分别以均方误差(Mean Squared Error, MSE)、平均绝对误差(Mean Absolute Error，MAE)、均方比例误差(Mean Squared Percentage Error，MSPE)以及平均绝对比例误差(Mean Absolute Percentage Error，MAPE)作为评价标准来比较分析混合Copula函数定价的精确性和可靠性.由于1000次的模拟次数充分保证了模拟结果的精确度，因此本文仅对模拟次数为1000的定价方法重复1000次，然后对这1000个重复定价的结果进行比较分析，从而探讨基于混合Copula函数的定价方法是否一致地优于其他方法，分析结果见表6.

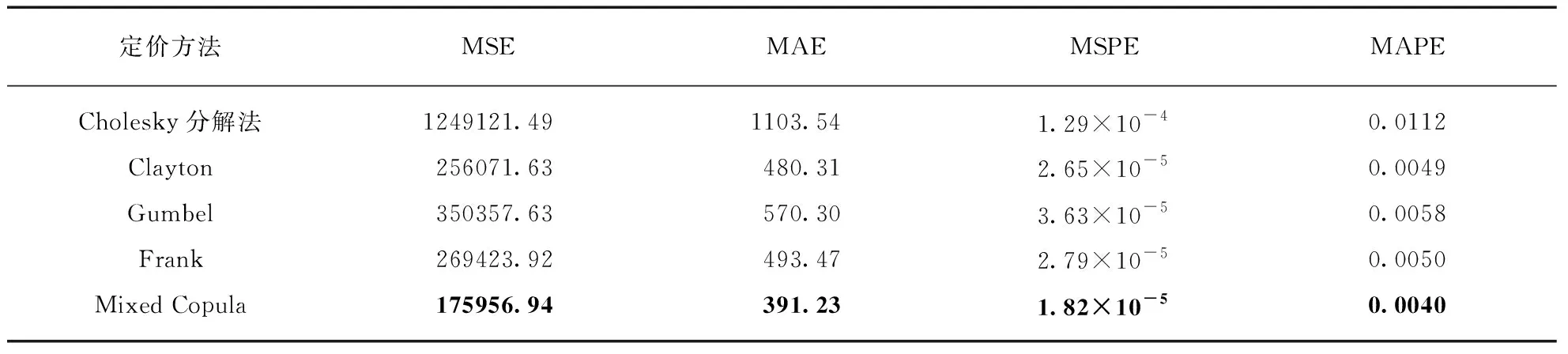
表6 Cholesky分解法、单个Copula函数以及混合Copula期权定价精度比较

注： 表中的粗体字表示定价过程中评价准则的最小值.

在所有定价方法中，基于混合Copula函数的蒙特卡罗模拟定价精度最高，其次是基于单个Copula函数的蒙特卡罗模拟定价，最后是基于Cholesky分解方法的蒙特卡罗模拟定价.众所周知，传统基于Cholesky分解法的蒙特卡罗模拟定价方法是建立在完全市场假说条件之下，然而现实市场大多为不完全市场，这导致其定价方法的偏误较大.而基于混合Copula函数的蒙特卡罗模拟定价方法脱离完全市场假说的局限，因而其定价更为接近理论真实值.总之，当标的资产的条件均值和条件方差被充分拟合的前提条件下，采用基于混合Copula函数的蒙特卡罗模拟定价方法能更精确地对多资产挂钩的结构性理财产品进行合理的定价.

另外，在对挂钩台湾加权指数和欧洲斯托克50指数且投资币种为人民币的理财产品进行定价分析时，本文相应地采用了台湾10年期政府公债利率和欧盟国债长期收益率作为无风险利率.而在对未来期望收益进行贴现时，我们则采用2014年4月份2年期中国人民币定期存款利率作为贴现率进行贴现.尽管本文目前没有考虑风险中性测度变换的问题，但是对于风险中性测度下，计价单位变换对多资产挂钩的理财产品的定价是否存在影响及影响程度如何，这将是我们下一步研究的方向.

4 结论及建议

本文以“法兴银行——2014年2年期股票指数挂钩人民币结构性理财产品”为例，研究基于混合Copula函数的蒙特卡罗模拟定价方法对多资产挂钩的结构性理财产品进行定价的合理性和精确性.通过对与该产品挂钩的标的物(即台湾加权指数和欧洲斯托克50指数)收益率序列进行分析，可以发现它们均为白噪声序列，且带t分布的EGARCH模型充分地捕捉各标的物序列的非线性、非对称性及尖峰厚尾性.通过基于混合Copula函数的蒙特卡罗模拟定价方法分析，文章发现该产品发行价格偏高，属于溢价发行.此外，文章的比较分析表明，基于混合Copula函数的蒙特卡罗模拟定价方法可以较好地运用于多资产挂钩的结构性理财产品的定价中，对理财产品的实际发行价格具有良好的拟合效果(理论值和真实值之间的价差为336元).在保证蒙特卡罗模拟收敛的条件下，不论模拟次数为多少，基于混合Copula函数的蒙特卡罗模拟定价方法一致地优于基于单个Copula函数和基于Cholesky分解法的蒙特卡罗模拟定价方法的精度.因此，在标的资产的条件均值和条件方差被充分拟合的前提条件下，基于混合Copula函数的蒙特卡罗模拟定价方法将对多资产挂钩的结构性理财产品进行更为精确、合理地定价.该实证分析的结果不仅对投资者购买结构复杂的理财产品具有一定的指导作用，还为理财产品发行者对产品更加精确的定价提供了理论基础.

一般来说，多资产挂钩的结构性理财产品较其他理财产品等更为复杂，其敏感度高、市场风险较大.另外，结构性理财产品的标的物具有一定的杠杆率.因此，如果持有人不善于管理风险，则有可能导致巨大的损失.尽管台湾加权指数以及欧洲斯托克50指数的历史波动率一直处于较低水平，但是为了确保其投资者利益，对理财产品实施有效的合约设计、交易制度和风险控制等措施是有必要的.然而，所有这些措施的实施基础在于对多资产挂钩的结构性理财产品进行合理、有效地定价.综合上述结论，本文对今后我国结构性理财产品市场的发展提出以下几点建议：

第一，我国资产管理机构应该不断提高对多资产挂钩的结构性理财产品的定价能力，实现对产品的精确定价，从而不断提高企业在金融市场中的核心竞争力.

关于多资产挂钩的结构性理财产品定价分析，目前业界通常采用的定价方法为基于Cholesky分解方法的蒙特卡罗模拟定价，然而该方法是建立在一些假设之上，与实际市场状况并不相符.而基于混合Copula模型的多资产挂钩的结构性理财产品定价方法不仅可以放松Cholesky分解方法中的一些限制条件，还可以显著提升产品的定价精度，使产品发行价格更贴近实际价值，从而保护投资者和产品发行者的利益.

第二，我国资产管理机构还应该不断加强多资产挂钩的结构性理财产品的创新能力，实现产品结构的多样化，进而满足不同偏好投资者的产品需求.

本文的研究表明混合Copula函数能够对金融资产间复杂的尾部相依结构进行精确刻画，因此，产品设计者在进行产品设计时，可以运用混合Copula函数对挂钩标的资产的尾部相依结构进行分析，根据不同风险偏好和风险承受能力设计出不同风险水平的产品，满足不同类型投资者的投资需求.