用矩阵求图中路径数目的另一种证明方法
2018-11-14王涛
王 涛
(长沙民政职业技术学院通识教育中心,湖南长沙410004)
一、问题的提出
1、用邻接矩阵表示有向图
如有向图D(图1所示)。

其A(D)(即图1的邻接矩阵)如下

此图的行从左往右表示v1,v2,v3,v4,此图的列从上往下表示v1,v2,v3,v4,矩阵中的元素aij
表示vi,邻接到vj长度是1的路径的条数(非负整数)
如v11(第一行,第一列)表示v1到v1长度为1的路径的条数是1(一个环)
2、利用矩阵的乘法求D中长度为2的路径数
如A2=A×A矩阵中元素aij表示vi邻接到vj长度是2的路径的条数(非负整数)

在结果矩阵中如v14=2(第一行,第四列)表示到v4长度为2的路径的条数是2。
这个2是第一个矩阵的第一行与第二个矩阵的第四列对应元素相乘,然后相加所得
2=1 ×1 +1×0+1×1+1×0
从图中可以观察到这两条路径分别是
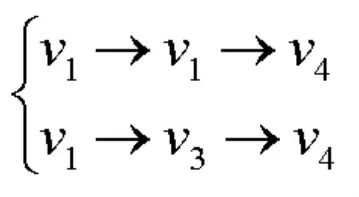
以此类推,因此我们可以得到定理;
矩阵AL中元素aij表示vi邻接到vj长度是L的路径的条数(非负整数)
接下来利用初等数学中的加法原理和乘法原理证明上述定理
二、定理的证明
如上的例子中v1到v4长度为2的路径的条数可以理解为
这件事情可以分成四类方式,每类方式可以分成两个步骤,分别是

第一类方式是v1→ v1→ v4,其中第一个步骤v1→ v1有1条路径,第二个步骤v1→ v4有1条路径,因此利用乘法原理可以得到第一类方式中共有路径的条数是1×1。
第二类方式是v1→ v2→ v4,其中第一个步骤v1→ v2有1条路径,第二个步骤v2→ v4有0条路径,因此利用乘法原理可以得到第二类方式中共有路径的条数是1×0。
第三类方式是v1→ v3→ v4,其中第一个步骤v1→ v3有1条路径,第二个步骤v4→ v4有1条路径,因此利用乘法原理可以得到第二类方式中共有路径的条数是1×1。
第四类方式是v1→ v4→ v4,其中第一个步骤v1→ v4有1条路径,第二个步骤v4→ v4有0条路径,因此利用乘法原理可以得到第二类方式中共有路径的条数是1×0。
所有最后用加法原理可得
1×1 +1 ×0+1×1+1×0=2
以此类推,可以证明
AL=AL-1A
矩阵AL中的元素aij表示vi邻接vj到长度是L的路径的条数(非负整数)。
三、结束语
本文利用了初等数学中的加法原理和乘法原理证明了离散数学中的一个很重要的定理,学生很容易理解。教材中有些重要定理的证明学生理解起来比较困难,教师要善于用简单的、学生容易接受的方法去重新证明,从而达到最好效果。
