面向分类错误率的自适应FAST算法

任胜兵,谢如良

(中南大学 软件学院,长沙 410075)

1 引 言

FAST[1,2](Feature from Accelerated Segment Test)算法是由Rosten、Porter和Drummond提出的一种新式简单快速的特征点提取算法,该算法不仅能大大降低特征点的检测时间,同时还能够迅速排除大量非特征点,因此被广泛应用到图像处理等实时系统中[3,4].

目前,在特征点提取领域中有大量的算法,如早期的SUSAN角点检测算法和Plessey算法等.在这些经典的特征提取算法之上,出现了大量的局部特征提取算法,如G.Lowe提出的尺度不变特征(scale invariant feature transform,SIFT)算法[5],该算法具有尺度旋转、亮度变化、缩放的不变性,但是它的特征检测计算量大,速度较慢,不适合实时应用[6].文献[7]提出了加速鲁棒特征(Speeded-up Robust Feature,SURF)算法,它是SIFT算法的一种改进,提高了特征点的检测速度,但是与FAST算法相比,速度还是相差较大.

近年来,FAST算法在实际应用中有大量运用,如图像配准[8]、机器人导航[9]、视觉跟踪[10]等领域.在学术上FAST算法也有大量的研究成果,如S.Taylor等[11,12]改进了FAST算法,使之能快速匹配并更具鲁棒性.但是FAST算法通常采用的阈值和半径是固定的,对于不同的图像,提取结果中会出现特征点冗余或者丢失的现象.例如,在多国纸币冠字号识别研究中,由于不同币种冠字号的字体和大小各异,因此FAST算法中固定的阈值与半径无法适应多种纸币.

针对以上缺陷,本文基于AdaBoost[13,14]提出了AdaBoost_FAST算法,其中AdaBoost算法的基本原理是通过在每轮迭代中降低正确分类样本的权重,增加错误分类样本的权重,使得分类器在迭代过程中逐步改进,最终将所有分类器线性组合得到最终分类器.其中本文使用到的分类器为支持向量机(support vector machine,SVM)[15],该方法是机器学习中一种重要的算法,被广泛应用于解决模式识别中的分类和回归分析问题中.本文根据AdaBoost算法的思想采用支持向量机进行训练,由分类器的错误率通过代价函数计算每组阈值和半径的抽样概率,当错误率越低,其抽样概率越大,对应的阈值和半径逐步接近最优值,所提取的特征点精度越高.根据抽样概率构成的代价函数可知,经过多次迭代以后,如果错误率较小并且无明显变化,则表明此时的阈值和半径已经达到最优.通过本文实验验证,该算法在保证FAST算法时效性的同时,能够有效地对阈值和半径进行自适应选择,减少了特征点冗余或者丢失的情况,提高了特征点提取的精确度.

2 FAST特征点提取算法

FAST算法所提取的特征点通常可以定义为:以r为半径的某个像素点邻域内,与该点处于不同灰度区域的像素点个数超过某一个阈值N,即有足够多的像素点的灰度值大于或者小于该点的灰度值.FAST算法所涉及的像素点分布如图1所示,中心点p为待判定像素点的像素值,当半径r为3时,周围共有16个像素点.

虽然FAST算法在时间效率上相比其他算法有明显的优势,但是由于其采用固定的阈值和半径,对于不同图像的特征点提取会出现冗余或者丢失的情况,导致提取的特征点精确度较低,难以取得良好的效果.例如在多国纸币冠字号识别中,如图2中所示,三种币种冠字号的字体大小以及形状存在明显的差异.当采用固定的阈值和半径时,图2(a)美元的特征点提取结果具有较高的代表性,并且精确度高.而图2(b)中的比索由于其字体形状较大,若采取同一阈值和半径,则会出现特征点的冗余,导致特征点提取结果不精确并且影响时间效率.图2(c)中,新西兰元的字体形状较小,采用此固定的阈值和半径时,则会出现特征点的丢失情况,极大降低了特征点的提取精度.

3 AdaBoost_FAST算法

为了解决FAST算法中阈值和半径不能自适应的问题,本文提出了AdaBoost_FAST算法,其基本流程如图3所示.

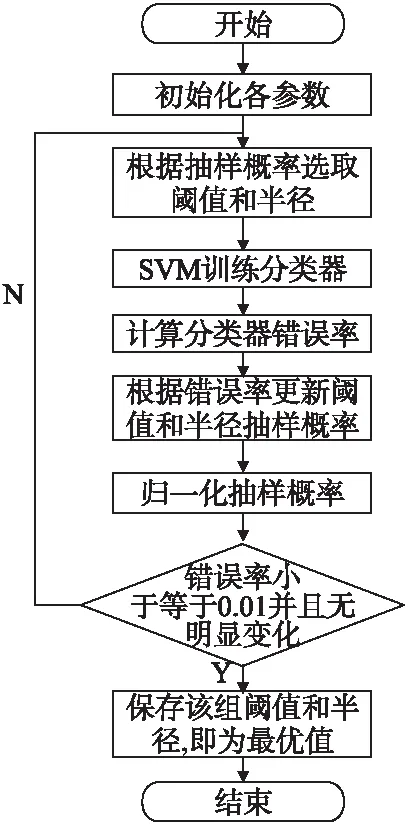
图3 AdaBoost_FAST算法流程图

AdaBoost_FAST算法的总体思路是依据分类器错误率来进行阈值和半径的自适应选择,根据错误率通过一个代价函数计算每一组阈值和半径的抽样概率.错误率越高,说明在该组阈值和半径下特征提取的效果较差,它的抽样概率就会越小,反之则越大.因此最优的阈值和半径的抽样概率将会逐渐变大,最终实现最优阈值和半径的自适应选择.

在此过程中,我们用变量Pt(j)表示第t次迭代的第j组阈值半径的抽样概率,它的初始值都设置为同一个值,意味着在第一轮迭代中所有的阈值和半径的抽样概率都是相同的.在每一轮迭代中,根据分类器的错分率更新每对阈值和半径的抽样概率,其中分类器采用支持向量机(support vector machine,SVM)来进行训练.根据所有训练数据的分布Dt来计算每个分类器ft的错分率,t是在第t轮迭代中选择核函数k的分类器错分率,如公式(1)所示:

t=

(1)

根据错误率计算并更新当前组的阈值和半径的抽样概率,如公式(2)所示.其中γ∈(0,1)是一个不变的参数,是更新阈值和半径对抽样概率的衰减系数.Pt+1(j)是更新后第j组阈值和半径的抽样概率.从公式(2)分析可得,当错误率越大,将会减小它在下一轮迭代的抽样概率.

Pt+1(j)←Pt(j)γ

(2)

在第t轮迭代完成以后,对阈值和半径的抽样概率进行归一化,如公式(3)所示,以确保抽样概率在(0,1)之间.归一化的步骤也是为了改变未被选择阈值和半径的抽样概率,其中ZP是归一化因子.

Pt+1(j)←Pt+1(j)/ZP,ZP=max(Pt+1+0.01)

(3)

当错误率不再发生明显变化并且错误率的值较小时(通常定义为错误率小于等于0.01),此时结束整个自适应迭代的选择过程,同时将此组中的阈值和半径保存,该值即是最优的阈值与半径,如公式(4)所示:

ft=argmin
ftt=arg

(4)

根据AdaBoost算法的收敛性可知,在多次迭代以后,分类器的性能会逐渐改进,最终达到最优.针对本文算法的收敛性分析,由公式(2)知,γ∈(0,1),表明(2)式是一个减函数.如果错误率t越大,则该阈值和半径在下轮迭代中,其抽样概率将会大大减小.如果错误率t越小,在下一轮的迭代中,其抽样概率将会增大.因此在本文算法中,当经过多次迭代以后,分类器错误率越小的,说明提取的特征点的精确度越高,其对应的阈值和半径抽样概率将会越趋近于1,算法中的最优阈值和半径最终将会收敛于错误率最小的分类器对应的阈值和半径.图4描述了AdaBoost_FAST算法的伪代码过程.

算法1.AdaBoost_FAST算法

INPUT:

训练样本:(x1,y1),…,(xN,yN)

核函数:k(·,·):X×X→

阈值半径对:(n1,r1),…,(nT,rT)

初始化训练样本的分布:D1(i)=1/N,i=1,…,N

初始化FAST算法中的阈值半径对的概率分布:Ρ1(j)=0.8,j=1,…,T

FAST算法中参数抽样衰减因子:0<γ<1

图4 算法伪代码

图4算法伪代码中,输入为相关数据集和参数的初始化,输出为最优分类器以及最优阈值和半径.算法1的1至9步是进行阈值和半径的最优化选择.其中第2至第3步是根据样本的分布抽取n个样本,根据抽样概率随机抽取一组阈值和半径.第4步根据已获得的阈值和半径对样本进行特征点提取.5到6步是训练分类器,并且计算训练错误率.第7步根据错误率更新阈值和半径的抽样概率.第8步即对抽样概率进行归一化操作.最后,进行T轮迭代后,如果满足错误率无明显变化且值小于给定的条件时,则结束整个迭代的过程.同时将此轮迭代中的阈值和半径保存,该值即为最优的阈值和半径,最终实现阈值和半径的自适应选译.

该算法在进行最优阈值和半径选择的过程中,根据算法1第7步的公式可知,最优的分类器所对应的阈值和半径的抽样概概率最大.即该组值将会参加多次迭代,所以重复阈值和半径的特征提取仅需操作一次,从而大大的减少了算法的运算量.在时间和空间效率上表现出了优越的性能.

4 实验结果与分析

4.1 实验设置

为了验证本文的AdaBoost_FAST算法能否有效地进行阈值和半径的自适应选择,我们在MNIST数据集*http://yann.lecun.com/exdb/mnist/上进行了实验验证,MNIST数据集是来自美国国家标准与技术研究所(NIST),其中训练集(training set)由来自250个不同人手写的数字和字母构成,其中50%是高中学生,50%来自人口普查局的工作人员.测试集也是同样比例的手写数字和字母.

在算法1中,首先给定阈值和半径一个取值范围,本实验中,阈值的取值范围为5～16,半径取值范围为1～5,阈值和半径对的初始抽样概率P1(j)都设定为0.8,训练样本的初始化分布D1为均匀分布.为了在时间效率上达到最优效果,我们根据经验将抽样衰减因子γ初始值设为2-5.整个实验将在Microsoft Windows xp(32位),2.7 GHz Intel CPU,4GB RAM的python3.5.1与opencv 3.0平台进行,其中SVM将采用libsvm进行求解.

4.2 阈值和半径自适应实验分析

4.2.1 阈值和半径自适应实验1

本文首先采用了MNIST数据集中的12000个训练样本.我们将按照字体大小将分成2组,一组为字体形状较大的(A组),另外一组为字体形状较小的(B组),由于大小不同的字体对应的最优阈值和半径各不相同,因此分成两组数据能够有效的验证本文算法的阈值和半径自适应选择的性能.本文算法自适应选择最优阈值和半径的整个迭代过程如图5所示.

图5 阈值和半径自适应收敛过程

图5中横轴表示自适应选择最优阈值和半径过程中的迭代次数,竖轴表示该次迭代经过支持向量机训练所得到的分类器的错误率.每一次迭代根据错误率更新当前组阈值和半径的抽样概率,当迭代到一定次数以后,错误率较高的分类器所对应的阈值和半径的抽样概率会逐渐变小,反之其抽样概率将会变大.而错误率最小的分类器,其对应的阈值和半径的抽样概率会逐渐趋于1.

如图5中的A组实验迭代到第13次时,已经开始收敛于最优值,此时最优的阈值和半径的抽样概率已经远大于其他的阈值和半径的抽样概率,并且在后续迭代过程中分类器的错误率都保持在一个较小的值,说明在该组阈值和半径下提取的特征点精确度高,因此该组阈值和半径为最优值.B组实验的阈值和半径的自适应选择过程和A组基本相同,B组在第12次迭代时已经收敛于最优阈值和半径.其中AB两组实验1至20次迭代所对应的阈值和半径以及错误率如表1所示.AB两组数据所取最优阈值和半径不同是由于A组字体形状较大,字体内部比较空旷,因此所采取的阈值和半径较大,而B组字体形状较小,只需要较小的阈值和半径就能保证提取到关键的特征点.综合两组数据,本文算法能够有效的通过分类器错误率进行阈值和半径的自适应选择,在选择的最优阈值和半径下提取的特征点精确度高,不会出现特征点丢失或者冗余的现象.

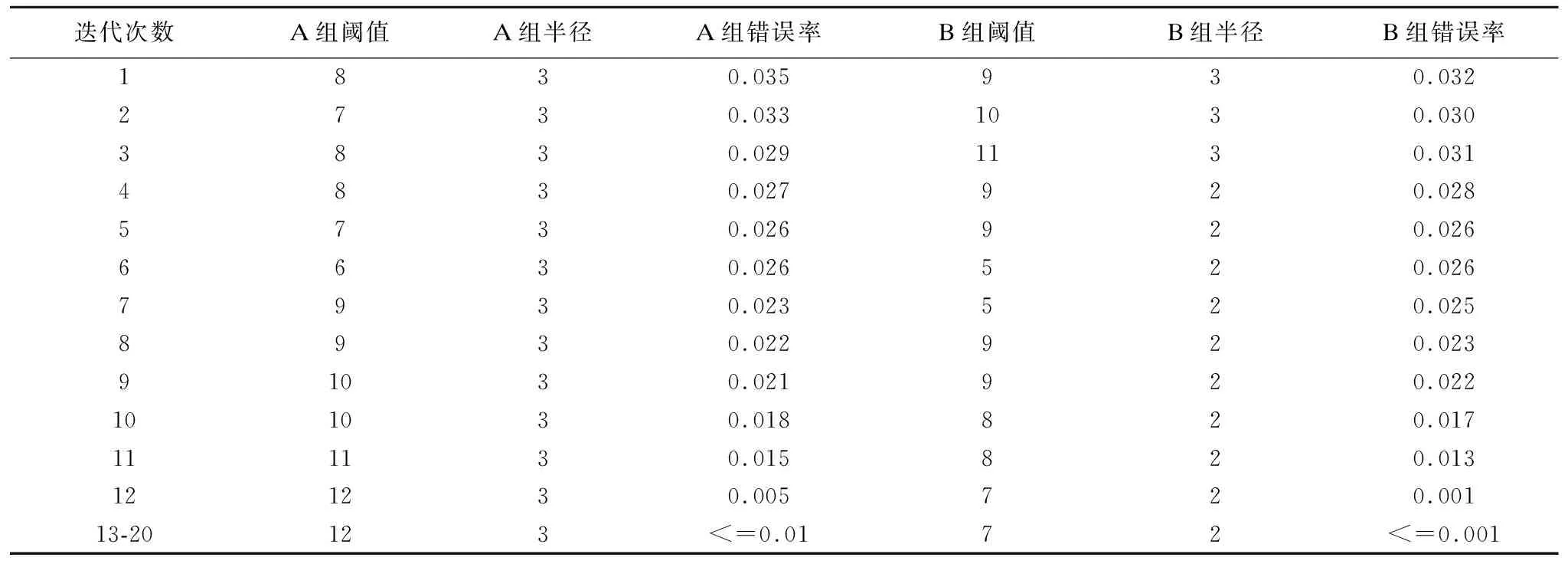
表1 AB组实验自适应选择过程中阈值半径和错误率表

4.2.2 阈值和半径自适应实验2

在4.2.1节的实验中,将样本分为字体大和字体小的两组,是为了说明阈值和半径的最优值与不同类别的图像是有关联的.为了进一步验证本文算法的自适应性,本组实验将不再按照字符的大小进行分组.而是将所有大小不同的手写体字分为一组,然后进行实验.从实验结果中,挑选出五组不同大小的字符,其中每一组中的字体大小相近,获取每一组的最优阈值和半径.得到的结果如表2所示.表2中,编号较小的组其字体较小,编号较大的组其字体较大.从表2的结果中分析可得,当将所有大小不同的样本混合进行实验时,本文算法同样能够根据图像字体大小的不同有效地自适应选择最优的阈值和半径.

表2 最优阈值半径和错误率表

在表2中,在字体较小时,即编号较小的组中,选择的是较小的阈值和半径.在字体较大的组中,根据FAST算法的原理,其最优阈值和半径应该较大.同时每组在选择出最优阈值和半径时,分类错误率也达到了较小.以上分析说明本文算法能够有效的自适应选择出最优阈值和半径.

4.3 AdaBoost_FAST与FAST的比较

为了验证本文算法在特征提取精度上的优势,本文在4.2实验的基础上,进行了两次特征提取实验.其中图6中分别给出了FAST算法和AdaBoost_FAST算法提取的部分图像的特征点分布图,从图6(a)中我们能够发现,当A组(字体形状较大)的图像与B组(字体形状较小)的图像分别采用FAST算法固定的阈值和半径时,图6(a)中字体形状较大的出现了特征点冗余,而字体形状较小的出现了特征点丢失的情况.而在图6(b)采用本文算法自适应选取最优的阈值和半径时,提取的特征点数量少,代表性高,特征点提取精度高,没有出现冗余的特征点,同时也没有出现特征点丢失的现象.

图6 部分图像特征点分布图

表3中的聚集率是衡量某一区域中是否有误检为特征点的一个指标,反应了特征点的丢失和冗余程度.假设M为图像中提取的总特征点数,Mc为周围聚集超过3个特征点的特征点总数,则聚集率可表示为公式(5).当c较大时,说明特征点存在冗余,如果c过小,即提取的特征点存在丢失的情况,根据实验结果观察所得c的值在百分之十左右时说明特征点的提取精确度高.

(5)

特征点重复率是表示算法的稳定性以及鲁棒性,假设在第一次实验与第二次实验中提取的特征点数分别为M1与M2,在第二次实验中提取到的特征点中与第一次实验中提取的特征点相重合的个数记为Mr,则特征点重复率的表达式如公式(6)所示,通常特征点重复率越高表示算法的稳定性越好.

(6)

表3中分别给出了本文算法以及FAST算法提取特征点的性能分析对比情况,其中源图像都相同,分别来自AB两组不同的十幅图像.从表3中可知,采用本文算法得到的特征点聚集率适中,提取精确度高,不会出现特征点丢失以及冗余的情况.而在表3采用FAST算法的实验中,A组聚集率比采用本文算法的A组高,明显出现了冗余的特征点,而B组的聚集率相比采用本文算法的B组低,说明出现了特征点丢失的情况.采用本文算法的AB两组数据通过两次实验得到的特征点重复率相比FAST算法较高,表明本文算法具有良好的稳定性.本文算法在进行最优阈值和半径选择时,会进行迭代计算,但是时间效率与FAST算法为同一个数量级,能够保证算法的实时性.

表3 AdaBoost_FAST算法与FAST算法特征点提取性能对比

4.4 参数选择实验

参数的选择能够影响算法在准确率以及时间效率方面的性能,本文算法中的参数包括迭代次数T,以及抽样衰减因子γ.为了检验这些参数的影响,本文进行了一系列实验来评估它们在算法中对阈值和半径自适应选择的准确性和效率性能的影响.将实验数据分成A、B、C三个组进行实验.

如图7所示,迭代通常进行到12-18次时,分类器的错误率已经收敛到较小的值,并且在后续迭代中能够保持稳定,因此已经收敛于最优阈值和半径.

图7 迭代次数与错误率变化

另一方面结合图8中的信息,随着迭代次数的增加,时间成本也是成线性增加.综合经验观察表明,当迭代次数选择为20时,阈值和半径自适应选择的准确性和效率性能都表现良好.

图9γ取值与时间效率的关系图中,三组数据中γ都取较大值时,时间增加较快.因为当γ值较大时,阈值和半径的抽样概率衰减幅度会较小.若要选择出最优的阈值和半径,迭代次数会增多,从而时间效率成本将会增大.结合图10中的信息,在不同γ的取值所对应的最优阈值和半径以及分类器错误率关系中.当γ取值大于0.03时,不同γ的取值所对应的分类器错误率都能够达到很小的值,即选择出的阈值和半径都为最优值.当γ的值远小于0.03时,阈值和半径的抽样概率衰减过大,导致大量阈值和半径都无法参与迭代过程,因此可能会错失最优值的选择以致分类器错误率较高.结合图9和图10的信息,本文根据经验γ的值选择为2-5.

图8 迭代次数与耗时变化

图9 gama取值与耗时关系

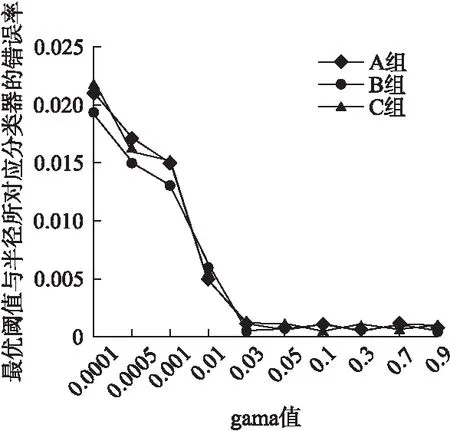
图10 gama取值与最优解的关系

5 结 论

本文提出了一种AdaBoost_FAST算法,该算法基于AdaBoost思想,根据支持向量机分类器错误率通过代价函数计算每组阈值和半径的抽样概率.经过多次迭代以后,最优的阈值和半径的抽样概率将会远大于其他值的抽样概率,逐步实现最优阈值和半径的自适应选择.实验结果表明,选取合适的参数值,该算法能够有效地进行阈值和半径的自适应选择,从而减少了FAST算法中特征点冗余和丢失的情况,提高了特征点提取精度,同时能够保证FAST算法的时效性,对于实时系统的应用具有重要意义.