一种逐跳方式的域内单节点故障保护算法
2018-11-14耿海军施新刚王之梁
耿海军,施新刚,王之梁,尹 霞
1(山西大学 软件学院, 太原 03000 2清华大学 网络科学与网络空间研究院,北京100084 3清华大学 计算机科学与技术系,北京100084)
1 引 言
近些年来,互联网的发展速度已经远远超出了人们的预期[1,2],并且互联网支撑的应用范围[3]也在不断扩大.互联网在迅速发展的同时,面临了新的挑战,其中域内路由可用性(Availability)[4]便是其中一个亟待需要解决的问题.相关研究[5]表明,网络中的故障频繁发生,并且不可避免.在故障修复期间,路由协议需要经历一段时间的收敛过程,在路由协议收敛过程中将有大量报文丢失,大大降低了路由可用性[6].然而,随着一些新型应用的出现,例如VoIP、在线游戏、视频[7-9],这些应用对网络时延提出了更加严格的要求[10,11].因此,如何提高网络可用性[12],降低路由协议收敛过程中报文丢失率,是互联网面临的一个重要挑战[13,14].为了解决该问题,学术界和工业界提出了路由保护方案[15],该方案预先计算备份路由,当网络出现故障时,利用事先计算好的备份路径转发受故障影响的报文,从而有效减少报文丢失率.
等价多路径( ECMP:Equal Cost Multiple Paths)[16]是最早使用的路由保护方案.当源地址和目的地址之间存在多条代价相等的最优路径时,利用等价路径作为其备份路径,该方案实现简单,支持增量部署.然而,该方案要求备份路径和最优路径具有相同的代价,虽然网络管理员可以通过调整链路代价达到该目的,但是该问题被证明是NP问题[17].因此,ECMP对网络可用性的贡献有一定的局限性.
IP快速重路由[18]方案以其独特的优势受到学术界和工业界的青睐,该方案利用无环路规则(Loop Free Alternates:LFA),计算备份下一跳,从而实现路由保护.该方案计算复杂度小,容易部署,因此大部分厂商的路由器支持该方案.然而,研究表明[19,20],利用该方案仅仅能保护50%左右的单故障情形.基于IP快速重路由框架,我们在文章[21-23]提出了一种高效的路由保护方案.该方案算法复杂度低,并且支持动态更新,支持增量部署,然而该方案的故障保护率和IP快速重路由的故障保护率接近.
为了进一步提高网络可用性,文章[24]提出了利用U-turn方案提高故障保护率,该方案可以在其邻居节点中计算LFA下一跳.U-turn虽然明显提高了故障保护率,但是仍然达不到预期目标.基于快速重路由和U-turn存在的缺陷,文章[25]提出了基于Not-Via地址的快速重路由方案.该方案利用辅助机制Not-Via地址,显式的表明网络中的故障,从而可用有效保护网络中所有单故障情形.虽然该机制可以大大提高网络的可用性,但是该机制的实现比较复杂,开销较大,不容易实际部署.
基于上述方案存在的缺陷,文章[26]提出了将基于IP快速重路由和基于Not-Via地址快速重路由结合的路由保护方案.该方案的基本思想是,当某节点存在IP快速重路由下一跳时,利用IP快速重路由方案,然而当该节点不在上述保护下一跳时,则利用基于Not-Via地址快速重路由计算保护下一跳.相比基于Not-Via地址快速重路由方案,融合方案大大降低了算法的复杂度,然而该方案仍然需要使用Not-Via地址,因此不容易实际部署.为了进一步降低上述融合算法的复杂度,我们在文章[27]中提出了一种高效的融合保护方案,该方案大大降低了算法的复杂度,并且故障保护率高,然而该方案部署复杂.文章[28]提出了利用O2方案来提高网络可用性.该方案基本思路如下,算法为每个节点计算两个到达目的地址的下一跳,当故障发生时,利用备份下一跳转发报文.然而,该方案对网络拓扑有一定的要求,并且计算复杂度较高.
2 单节点故障保护算法
2.1 基本模型
网络拓扑结构可以用图G=(V,E)来表示,其中V表示网络中路由器的集合,E表示网络中链路的集合.对于网络中的某条链路e=(x,y)∈E,用w(e)代表该链路的权值,该值可以是跳数、时延、带宽、能耗等,也可以是其中这几个度量的组合.假设源地址为s,目的地址为d,P(s,d)表示源到目的的最优下一跳;B(s,d)表示源到目的的备份下一跳;SP(s,d)表示源到目的的最优路径;C(s,d)表示源到目的的最优路径的代价.
定义1.在网络拓扑G=(V,E)中,对于该网络中的任意一个目的地址d,称Td(V,Ed)是以节点d为根的最优路由树,当且仅当满足下面两个条件:
1)Ed⊂E,|Ed|=|V|-1;
2)对于树中的任意一个节点v∈E,该节点到目的地址d的路径具有最小的代价;
定义2.在最优路由树Td(V,Ed)中,对于树中的任意一个节点v∈V,child(v)表示该节点的所有孩子节点,parent(v)表示该节点的父亲节点,subtree(v)表示以该节点为根的子树中的所有节点.
定义3.在以目的地址d为根的最优路由树中,对于该树中的任意一个节点v∈V-d,假设该节点出现故障.当节点u∈child(v)时,如果存在一条链路(x,y),使得x∈subtree(d,u)和y∈V-subtree(v)-d同时成立,则称链路(x,y)是子树subtree(u)的第一类桥,用Candidate(u)={(x,y)}表示;当节点w∈child(v)时,如果存在一条链路(p,q),使得p∈subtree(u)和q∈subtree(w)同时成立,则称链路(p,q)为子树subtree(u)和子树subtree(w)的第二类桥,用Candidate2(u)=Candidate2(w)={(p,q)}表示.第一桥和和第二类桥统称为桥,用Candidate来表示.
定义4.对于任意事件(u,d,f),其中u表示源地址,d表示目的地址,f表示u到d的最优路径SP(u,d)上的单节点故障.当该事件出现时,如果u到d依然存在别的路径,二者仍然保持连通.即该网络图中不存在割点,当该网络拓扑结构中的任何一个节点出现故障时,都不会影响该网络的连通性,则称该网络具有健壮拓扑结构.
定理1. 对于一个健壮的网络拓扑结构,假设节点f出现故障,节点f有k个孩子节点,分别用(f1,f2,…,fk)表示,则必定存在一个孩子节点fx∈child(f),该孩子节点对应的子树subtree(fx)至少有一个第一类桥;当某个孩子节点fy∈child(f)对应的子树没有第一类桥时,则该孩子节点对应的子树subtree(fy)至少有一个二类桥.
证明:下面使用反证法来证明该定理.
首先证明该定理的前半部分.当节点f出现故障时,假设节点f的所有孩子节点都没有第一类桥.即对于任意节点fx∈child(f)不存在任何链路(p,q),使得p∈subtree(fx)和q∈V-subtree(f)-d同时成立.那么对于任意节点p∈subtree(fx),与节点p相连的链路的另一端q仅仅和集合subtree(fx)中的结点相连,q到d的最优路径必定经过节点f.根据上述描述可知,当节点f出现故障时,节点fy∈child(f)对应的子树中的节点将无法到达目的.这与健壮的网络拓扑结构的前提假设相矛盾.因此该定理的前半部分成立.
下面证明该定理的后半部分.当节点f出现故障时,对于节点fy∈child(f),当该节点对应的子树没有第一类桥时,假设该节点对应的子树也不存在第二类桥.即对于节点fy∈child(f),不存在任何链路(m,n),使得m∈subtree(fy)和n∈subtree(fk)同时成立,其中fk∈child(f).那么对于任意节点m∈subtree(fy),与节点m相连的链路的另一端n仅仅和集合subtree(fy)中的结点相连,n到d的最优路径必定经过节点f.根据上述描述可知,当节点f出现故障时,节点fy∈child(f)对应的子树中的节点将无法到达目的.这与健壮的网络拓扑结构的前提假设相矛盾.因此该定理的后半部分成立.
根据上述证明可知,该定理成立.
定义5.在网路拓扑中,假设节点f出现故障.对于任意的源-目的(s,d),当源到目的的最优路径经过节点f时,即:f∈SP(s,d),则s到d的最优路径将无法连通.如果fx∈child(f),(x,y)∈Candidate(fx)和(x,y)∈RP(s,d)成立,其中RP(s,d)表示节点s到节点d重路由路径,则称该桥为RP(s,d)的有效桥.
引理1.在网路拓扑中,假设节点f出现故障,对于其孩子节点fx∈child(f),如果桥(x,y)∈Candidate(fx)是第一类桥,则该桥一定是有效桥;如果该桥是第二类桥,则该桥不一定是有效桥.
证明:当节点f出现故障时,对于其孩子节点fx∈child(f),如果桥(x,y)∈Candidate(fx)是第一类桥,其孩子节点fx的重路由路径可以表示为RP(fx,d)=(fx,…,x,y,…,d),因此(x,y)∈RP(fx,d),即第一类桥一定是有效桥.当桥(x,y)∈Candidate(fx)是第二类桥时,假设fk∈child(f),y∈child(fk),则(x,y)∈Candidate(fy).当子树fk只有该二类桥,不存在别的桥时,节点fx的重路由路径将不包含该桥.这是因为如果节点fx的重路由路径将包含该桥,则当报文转发到节点y时,节点y到目的的最优路径必然经过节点f,而子树fk没有别的桥,因此报文将无法被正确转发到目的地址.相反,当子树fk存在别的桥时,节点fx的重路由路径可能包含该桥.因此,第二类桥不一定是有效桥.
2.2 路由保护算法
本节将重点解决3个问题:
1)如何找出子树对应的有效桥;
2)如何选择最佳的桥,从而使得重路由路径具有最小的代价;
3)如何为节点计算保护下一跳.
根据引理1可知,某节点对应的子树可能存在两类桥,第一类桥一定是有效桥,而第二类桥不一定是有效桥,因此为了计算有效桥,算法需要计算出该子树对应的所有桥,然后从中选择有效桥.因为子树对应的桥的数量可能会很多,如果在算法中计算出所有桥,然后再从中选择有效桥,该方案将会增加算法的时间复杂度.因此,为了降低算法复杂度,本文对桥的优先级做了如下规定,第一类桥的优先级大于二类桥的优先级,当某个节点的子树拥有第一类桥时,不再为其计算第二类桥.如果某个节点的子树只有第二类桥时,只为其计算有效第二类桥.
下面描述如何为子树选择最佳桥,如何为节点计算备份下一跳.由于对于任意的目的节点计算方法都是类似的,因此,不失一般性,算法仅仅考虑目的地址为d的计算方法.在下面的描述中,对节点的颜色做了区分,所有节点的初始颜色都是白色;当节点f出现故障时,当fx∈child(f)时,将子树subtree(fx)中的所有节点标记为黑色,表示将要为该子树计算最佳桥;当为该子树计算出有效桥时,将该子树中所有节点标记为灰色.
2.2.1 子树有第一类桥
当节f点出现故障时,节点fx∈child(f)对应的子树有第一类桥.将子树subtree(fx)中的所有节点标记为黑色,根据深度优先算法遍历子树subtree(fx)中的所有节点,对于该子树中的节点p,检查它的每一个邻居节点q,如果该节点不是黑色,则链路(p,q)为子树subtree(fx)的桥,由公式(1)
C(fx,p)+C(p,q)+C(q,d)
(1)
计算重路由路径的代价.该公式中涉及到的变量都可以很容易的从链路状态路由协议中得到.其中cost(p,q)可以从链路状态数据库中得到,其余变量可以通过Td得到,因此很容易计算相应的桥对应的重路由路径的代价.对于找到的所有桥,选择具有最短重路由路径的一个作为最终的桥.最后为相应的节点计算保护下一跳.根据选定的桥,计算节点fx的重路由路径,假设该路径为(fx,m1,m2,…,mk,p,q), 则相应节点的保护下一跳为:B(fx,d)=m1,B(m1,d)=m2,…,B(p,d)=q.最后,将子树subtree(d,fx)中的所有节点标记为灰色.
2.2.2 子树只有第二类桥
当节点f出现故障时,节点fy∈child(f)对应的子树只有第二类桥.根据广度优先算法遍历子树subtree(d,fy)中的所有节点,寻找首次出现的一条边(m,n),其中m是黑色,n是灰色,则链路(m,n)即为该子树的最佳桥,最后将子树subtree(fy)中的所有节点标记为灰色.根据同样的方法计算重路由路径的代价和保护下一跳.
算法1描述了如何为节点的子树计算有效桥,如何选择最终桥,如何为节点计算保护下一跳.算法将为每个节点计算一个最优下一跳和一个备份下一跳.当网络出现故障时,不受该故障影响的节点依旧按照最优下一跳转发报文,受该故障影响的节点将报文转发给备份下一跳.将所有节点的备份下一跳设置为空,所有节点的颜色标记为白色(算法1中的第1-4行).对于目的节点d,根据深度优先算法遍历以d为根的最优路由树中的所有节点,当访问某个节点v时,假设该节点出现故障.假设节点v有k个孩子节点,分别用(v1,v2,…,vk)表示.首先,将子树subtree(v)中的所有节点标记为黑色,其余节点标记为白色(算法1中的第7行).如果节点v的孩子节点已经有了备份下一跳,则将该孩子节点对应的子树全部标记为灰色,(算法1中的第8-12行).
算法重复执行下面的步骤1-步骤3,直到除去节点 外,没有黑色节点.
1)根据深度优先算法遍历子树subtree(v)中的所有黑色节点.
1.1)如果存在第一类桥,计算具有最短保护路径的一个桥作为最终的桥,记为(m,n),(算法1中的第15-26行).
1.2)如果不存在第一类桥,根据广度优先算法遍历子树subtree(d,v)中的所有黑色节点,计算出第二类桥,记为(m,n),(算法1中的第27-31行).
2)寻找节点m对应的子树的根节点,并且将子树中所有节点标记为灰色,(算法1中的第32-33行).
3)根据选择的最终桥为相应节点计算保护下一跳(算法1中的第34行).
Algorithm1. Node-protection(d)
//每个节点计算到目的地址d的备份下一跳
Input: v∈V,G(V,E),目的地址d
Output: B(,d)
1.Forv∈Vdo
2.B(v,d)← φ;
3.v.color← white;
4.EndFor
5.计算Td(V,Ed),并且存储节点到d的最优下一跳;
//按照深度优先顺序访问Td(V,Ed)中的节点;当访问某个节点时,假设该节点出现故障.
6.Forv∈V且v≠ddo
7.将subtree(d,v)中的所有节点标记为黑色;
8.Foru∈child(v)do
9.IfB(u,d)≠φthen
10.将subtree(u)中的所有节点标记为灰色;
11.EndIf
12.EndFor
13.mincost← ∞;
14.Flag=0;
15.Form∈subtree(v)并且m是黑色节点do
16.For每个与节点m直接相连的节点ndo
17.Ifn是白色的then
18.Flag = 1;
19.value=C(m,d)-C(v,d)+C(m,n)+C(y,d)
20.Ifmincost≥valuethen
21.m← x
22.n← y
23.EndIf
24.EndIf
25.EndFor
26.EndFor
//如果不存在第一类桥
27.IfFlag=0then
//利用广度优先遍历subtree(v)中节点
28.Form∈subtree(v)并且m是黑色do
29.寻找首次出现的一条边(m; n),其中m是黑色, n是灰色;
30.EndFor
31.EndIf
32.寻找节点m所在的子树,使m∈subtree(f ),其中f∈child(v)
33.将subtree(f)中的所有节点标记为灰色;
//表示已经为该子树计算出有效桥
34.AssignBackup(m,n,f,d);
//如果不存在第一类桥,则计算有效第二类桥.
35.EndFor
36.return Backup(,d)
Algorithm2. AssignBackup(x,y,v,d)
//为路径SP(x,v)上的所有节点计算备份下一跳,其中(x,y)为子树v的桥
1.u←x;
2.v← y;
3.Whileu≠vdo
4.IfB(u,d)=φthen
5.B(u,d)←v;
6.v←u;
7.u←Primary(u);
8.EndIf
9.EndWhile
图1描述了当节点a出现故障时,算法为其孩子节点计算备份下一跳的过程.
1)找出所有以a为根的子树(节点a除外)的桥{(g,k),(i,l),(i,m)}.因为该子树有第一类桥,所以不再为其计算第二类桥.当选择(g,k)作为该子树的桥时,节点e的重路由路径的代价最小,因此选择链路(g,k)作为以e为根的子树的最终桥,并且将以e为根的子树标记为灰色.根据选择的最终桥可知,节点e的重路由路径为RP(e)=(e,g,k,j,d),因此B(g,d)=k,B(e,d)=g.
2)找出所有以a为根的子树(灰色节点和节点a除外)的桥{(c,g),(f,i)},并且将以c为根的子树标记为灰色.因为该子树只有二类桥,根据算法只选择一个桥即可,因此选择链路(c,g)作为以c为根的子树的最终桥.在选择桥时,只考虑和灰色节点相连的链路,因此选择的桥都是有效桥,从而保证算法的正确性.根据选择的最终桥可知,节点c的重路由路径为RP(c)=(c,g,k,j,d),因此B(c,d)=g

图1 计算备份下一跳实例
3)找出所有以a为根的子树(灰色节点和节点a除外)的桥{(b,c)},并且将以b为根的子树标记为灰色.根据选择的最终桥可知,节点b的重路由路径为RP(b)=(b,c,g,k,j,d),因此B(b,d)=c.
定理2.当网络中的所有节点都部署上述的路由保护算法时,可以保护网络中任意单节点故障.
证明:在网路拓扑中,假设节点f出现故障.对于任意的源-目的(s,d),当源到目的的最优路径经过节点f时,根据定理1可知,子树subtree(f)至少存在一个有效桥,则算法可以保护节点f. 由于节点s是节点f的子孙节点,则当节点f断开时,从源节点s发送到目的节点d的报文可以正常到达.
2.3 转发算法
对于任意目的节点,每个节点在转发表中维护两个下一跳,分别是最优下一跳和备份下一跳.节点通过运行路由协议,计算出最优下一跳,运行路由保护算法,计算出备份下一跳.根据上述算法可知,当网络中出现单节点故障时,某些节点对应的重路由路径可能需要经过多个桥.因此可以利用MPLS来配置备份路由,然而该方案需要额外的控制信息,开销比较大,不容易实际部署.因此,本文的方案采用纯IP协议实现,利用了IP包中的TOS( Type of Service)字段,该字段的数值记录节点重路由路径经过的第二类桥的数量.在实际网络中可以通过双向转发检测机制(BFD,Bidirectional Forwarding Detection)快速检测网络中的节点故障.下面是具体的报文转发过程,当某个节点收到报文时:
1)该节点不是从最优下一跳接收到报文.
1.1)若该报文头部的TOS字段值为0,将分两种情况:
1.1.1)该节点到目的节点的最优下一跳没有故障,则将报文转发给最优下一跳.
1.1.2)该节点到目的节点的最优下一跳出现故障,该节点将修改报文头部的TOS字段,将报文转发给备份下一跳.
1.2)如果该报文头部的TOS字段值不为0时,则将报文转发给备份下一跳,并且将TOS字段的值减1.
2)该节点从最优下一跳接收到报文,该节点到目的的最优路径必定出现了故障,因此该节点需要将报文转发给备份下一跳.
从上述的转发方式可以看出,本文提出的算法和目前互联网采用的路由算法都是采用的逐跳转发方式.
3 实验及结果分析
为了全面准确的说明上述算法的性能,将在试验中采用多种拓扑结构.其中包括Abilene[29],利用测量工具Rocketfuel[30]测量拓扑结构,利用模拟软件Brite[31]产生的拓扑结构.
1)Abilene是一个实际运行的网络拓扑,由11个路由器和14条链路构成.
2)本文在Rocketfuel测量出的拓扑中选择6个拓扑,其参数在表1中列出.
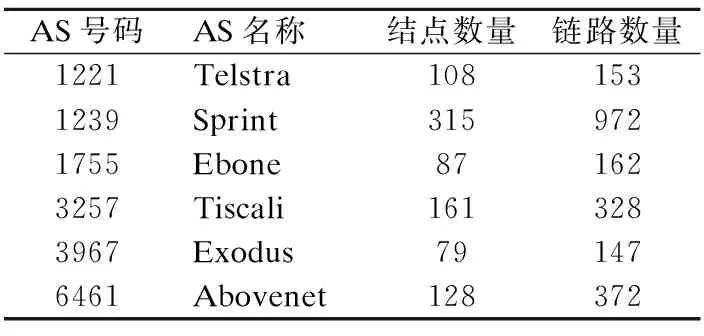
表1 Rocketfuel拓扑参数
3)利用模拟软件Brite产生拓扑的具体参数见表2.

表2 Brite生成拓扑结构的参数设置
3.1 故障保护率
本节将利用故障保护率来评价不同算法应对网络中单节点故障的能力.故障保护率定义为:受保护节点的数量/网络中所有节点的数量.从该定义可以看出,对于同一拓扑结构,故障保护率越高,该算法的性能越高.
表3描述了不同算法对应的故障保护率,该表中采用真实拓扑和测量拓扑模拟实验.从该表中可以得出结论,本文算法可以100%保护网络中所有出现的单节点故障情形,LFA和U-turn只能保护部分单节点故障.本文算法的故障保护率明显高于LFA和U-turn.

表3 不同算法对应的单节点故障保护率
图2表示故障保护率和网络中节点平均度的关系,采用Brite软件生成拓扑模拟实验,可以看出,本文提出的算法始终保持100%故障保护率.LFA和U-turn的故障保护率随着节点度的增加而增加,但是仍然无法提供100%故障保护率.当网络平均节点度为30时,LFA和U-turn的故障保护率分别为63%和81%.

图2 故障保护率随着节点平均度变化情况
3.2 路径拉伸度
当网络发生故障时,受该故障影响的路径的代价必定会发生变化.因此,下面将讨论网络发生单节点故障后,算法对应的路径拉伸度.路径拉伸度表示为:当网络中发生故障时,重路由路径的代价/最短路径代价.路径拉伸度越大,重路由路径代价越大,对资源的消耗越大,相反,路径拉伸度越小,重路由路径越接近最优路径.
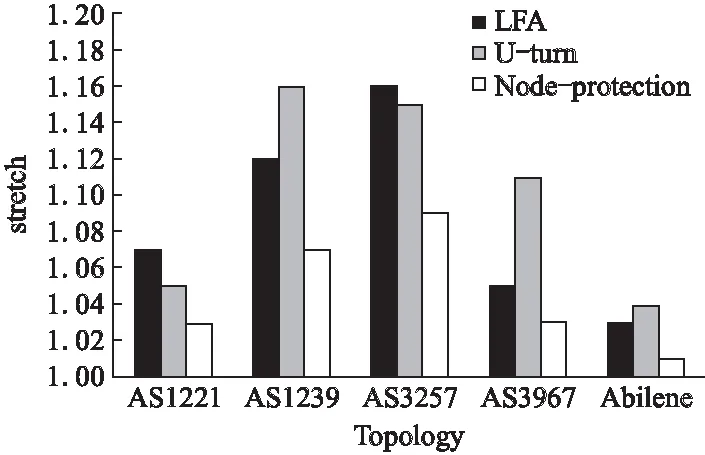
图3 路径拉伸度
下面详细描述实验过程,对于某个网络,随机的选择某个节点发生故障,然后利用不同的算法计算重路由路径,最后计算出相应的路径拉伸度.图中的数值表示重复上述实验100次后计算平均值.
图3描述了不同算法在相应的拓扑结构中对应的路径拉伸度.从该图中,可以看出,本文路径拉伸度明显低于LFA和U-turn.这是因为LFA和U-turn采用随机方法选择备份下一跳,而本文算法从所有备份路径中选择代价最小的下一跳作为备份下一跳.因此,本文提出的算法对应的重路由路径更加接近最优路径.
4 结束语
针对目前互联网部署的域内路由协议存在的可用性问题,本文提出了一种有效的单节点故障路由保护方案.该方案与目前互联网部署的域内路由协议是兼容的,因此支持增量部署,容易在实际环境中部署.理论和实验结果表明,该方案可以100%保护网络中所有出现的单节点故障情形,达到了预期目标经.本文提出的方案主要针对网络中单故障情形,因此下一步将重点研究如何将该算法应用在并发故障情形.
