合作学习：开启数学深度学习之旅

江丽娟（建瓯市东峰中学，福建 建瓯 353100）

数学课堂气氛过于沉闷，学生参与意识淡薄，缺少探究的能力，就会日渐变得麻木、呆板，消极沉默，失去积极的学习态度，学习能力大幅减弱。在这样的课堂上，学生封闭自我，不懂的问题既不愿意去请教教师，也不喜欢和同学交流，学习兴趣完全丧失，难以形成良好的学习习惯，学生没有真正成为学习的主人。如何让学生真正成为学习的主人？在笔者学校推行“三环六元九式”教学模式过程中，笔者对这一问题有过许多思考与实践研究，在指导学生自主预习、组织小组合作学习、鼓励学生质疑问难、拓展学习内容等方面，累积了以下一些心得与体会。

一、自主预习，明确目标

教师应该教会学生学会学习，学会找到适合于自己的学习方法。在教学中，要提高学生的自学与解题能力，就必须抓好“预习”这一环节。

例如：在教学《13.3.2等边三角形的性质与判定》时，我们曾尝试建构“先学后教，自主互助”的教学模式，在课前按教学目标制定好导学案，让学生带着导学案的问题去自学：（1）学过的等腰三角形有哪些性质与判定？（2）等边三角形有什么性质与判定？（3)等腰三角形与等边三角形之间有什么联系与区别？让学生在课前一边自主预习看书，一边在小组内进行讨论。依次可得出：（1）等边三角形的三条边都相等，等边三角形的三个内角都相等，并且每一个角都等于60°；（2）等边三角形是轴对称图形，它有三条对称轴，等边三角形是特殊的等腰三角形；（3）三边都相等的三角形是等边三角形；（4）三个角都相等的三角形是等边三角形；（5）有一个内角等于60°的等腰三角形是等边三角形等有关知识。在第二天课堂上，同学们个个充满激情、跃跃欲试，都想在班级展示汇报自己小组自主获得的有关等边三角形的性质及判定的结论。

这样，课前让学生通过教师制定的导学案，带着问题去探究，让学生在小组内进行互助交流，可以激发学生的学习兴趣，培养其自主探究的能力。

二、课堂转型，小组合作

心理学家罗杰斯提出：“有利于创造活动的一般条件是心理自由和心理安全。”以往我们采用的多是教师唱独角戏的授课方法，这样的课堂上，学生的表现机会较少，师生、生生之间缺少交流，压抑了学生自由发挥的天性，不利于学生创造性思维的发展。学校的“三环六元九式”教学模式下的课堂倡导民主、宽松、和谐，学生成为课堂的主人，这种新型的课堂模式可以唤醒学生内心深处对学习的渴望，使学生对学习有一种自由感、成就感、自豪感。

学习弱的学生在原先的课堂上畏于教师的权威，听不懂的不敢问、不敢说，形成恶性循环。而小组合作的方式让学生在学习困难时能及时释疑解惑。他们受到小组同学的影响与帮助，会参与到讨论中，渐渐地建立学习的自信，开始主动地探究，在课堂上大胆发表自己的看法。学习好的同学强强联手，在积极的思辨过程中更是大有收获，大部分困难得到了解决，学习效益倍增。

例如，在探索《圆与圆的位置关系》的教学中，改变以往的教学模式——不是直接把圆与圆的5种位置关系传授给学生，而是请各小组把课前准备的两个圆拿出来进行小组讨论。各组都非常积极地投入到活动中，且都进行了合理的分工，有的记录，有的动手拿圆演示，大组长指导小组活动。小组内进行讨论交流5分钟后，由各小组进行展示活动结果。前面三组都展示操作了圆与圆的所有的位置关系，那么圆与圆还有同心圆，又是属于什么关系呢？第四小组刚提出疑问，第三小组马上就有人回答，其实同心圆属于内含的一种特殊情况。

小组讨论，学习环境相对轻松，他们各抒己见，有的发表独立见解，有的纠正他人错误，有的还能将几个同学的想法整合为一个相对完整的想法。

三、集思广益，多向交流

在小组互助学习中，学生们互相取长补短。交流可以多向交叉进行：组内成员交流、组与组交流、小组与教师交流。这些交流可以分开，也可以同时进行。

例如，在教学《切线的判定定理》中，先在小组内探讨直线和圆相切的方法，总结得出“有交点，连半径，证垂直；无交点，作垂直，证半径”的解题思路。教师在小组中巡回指导。

在讲解判定的应用时，给了一个例题进行合作交流。交流可以组内进行，也可以在小组与小组之间进行。

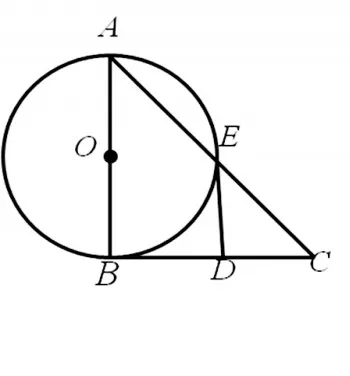
例题：如图所示，△ABC是直角三角形∠ABC=90°，以AB为直径的⊙O交AC于点E，点D是边BC的中点，连结ED，求证：DE与⊙O相切。

几分钟的讨论结束后，小组展示交流结果。第一、二小组组合选出小老师展示：连接OE、OD，∵O为AB的中点，D为BC的中点∴OD∥AC∴∠EOD=∠OEA，∠BOD=∠A，又 ∵OE=OA，∴∠A=∠OEA，∴∠EOD=∠BOD，又 ∵ OB=OE，OD=OD，∴ △ BOD≌△ EOD，∴∠OED=∠ABC=90°，∴DE与⊙O相切。第三小组展示：连接OE、BE，∵AB为⊙O的直径，∴∠BEC=90°，在Rt△BEC中，D为BC的中点，∴DE=0.5，BC=BD，∴∠DBE=∠DEB，又∵OB=OE，∴∠OBE=∠OEB，又∵∠OBE+∠DBE＝90°，∴∠DEB+∠OEB＝90°，∴OE⊥DE，∴DE与⊙O相切。前面两组展示了证明的不同解题的思路，接着第四、五、六小组组合表示还有不同的解法：连接OE、BE，∵AB为⊙O的直径，∴∠BEC=90°，在Rt△BEC中，D为BC的中点，∴DE=0.5BC=CD，∴∠C=∠DEC，又∵OE=OA，∴∠A=∠OEA，又∵∠ABC＝90°，∴∠A+∠C＝90°，∴∠DEC+∠OEA＝90°，∴∠OED＝90°，∴OE⊥DE，∴DE与⊙O相切。

一题多解，若用以往的教学模式，在课堂上只能讲解一种解法。现在通过自主互助，合作交流，大伙集思广益，既提升了学生的倾听、说话、交流能力，也实现学生在课堂的多元价值。

四、质疑问难，拓展学习

教育学家朱熹说：“读书无疑者，须教有疑，有疑者却要无疑，到这里方是上进。”教师要善于引导学生大胆质疑，鼓励学生对教材上的内容质疑，敢于对教师的讲解内容进行质疑，特别是对同学的观点进行质疑。教师对学生进行有效的引导，师生的思维火花相互碰撞，学生的个性才会有彰显的机会。

例如，讨论关于x的方程ax=b的解的情况。预定前十分钟在小组内进行思考、讨论，后二十分钟每个小组进行展示、交流结果。课堂上，教师从学生的表情、动作和嘈杂声中可以判断学生已经否定了“方程永远只有一个解的结论。约十分钟后，第一、二小组展示了当a≠0时，方程只有一个解时，方程无解。笔者对学生进行了肯定，因为他们已经意识到必须对字母系数进行讨论。第三、四小组对后一种情况提出疑问：当a=0时，方程的解与b的取值是否有关？此时学生短时间的沉默转为更加热烈的讨论。几分钟以后，第五小组同学最先统一认识，得出结论：当a≠0时，方程只有一个解当a=0且b=0时，方程有无数个解，即x可以取任意数；当a=0且b≠0时，方程无解。这时，教师接着再安排学生在小组内进行讨论、消化，就会收到很好的教学效果。

五、加强反思，提升学力

“先学后教，自主互助”的课堂教学模式会引导学生在课后对当天所学的数学知识进行总结反思。回顾自己在学习过程中的收获和感悟，是一种反思性学习。在课堂小结时，教师务必注意要给学生表现的机会，让学生在课堂中学会总结自己的所学知识，对课堂出现的错误进行反思。有时可以让学生对课堂学习的知识进行适当地扩展练习，加强和提升解题能力。