重载磁力轴承力学特性和热特性分析与优化*
2018-11-13
(北京化工大学机电工程学院)
0 引言
磁力轴承是集电磁学、转子动力学与控制科学为一体的产物,通过改变输入电流的大小和角度产生用来抵消转子因不平衡产生的干扰力,同时体现了磁能和机械能之间的转化。磁力轴承就是利用电磁力具有可控制性这一优势,应用于振动控制和在线检测等领域[1]。针对离心压缩机会产生不同形式的流体激振力,由此使转子产生相应的振动[2],电磁轴承的应用可以高效快速地对该振动进行调控。磁力轴承的定子和转子采用了硅钢片材料,该材料具有非线性的磁导率,会在工作时达到磁饱和、并出现漏磁、磁路耦合以及涡流损耗等现象,这些损耗将会以热量的形式散发到环境中,从而极大地降低了磁力轴承的工作效率。因此对磁力轴承的电磁场以及温度场进行理论、仿真和实验的研究很有意义。
工业的飞速发展,推动了电磁控制在压缩机转子振动稳定性方向的深入研究,利用电磁进行控制的需求也越来越大。研究人员利用磁力轴承的支撑特性在鼓风机、脉冲电源系统、控制器以及空心轴和离心叶轮的转子系统中都有了应用[3-6],通过优化设计极大地提高了工作效率。而对电磁结构优化和由损耗产生的温升变化也有不少研究。学者研究出了多种结构优化的方法:电磁力与磁通密度的变化规律、单位长度的最大承受能力以及体积最小等优化原则[7-8]。Gerhard Schweitzerh等人对磁力轴承的机械结构、轴承中的损耗等做了详细的介绍,并且提出了可以降低损耗的方法[9-10]。在温度场分析中Xiaojun Ren等将计算的磁轴承损耗为作为热源加热,模拟对磁力轴承的温升变化[11]。周灿等人对电主轴系统进行了不同转速下的温度分析[12]。学者们也分别对电磁阻尼器以及电磁离合器等结构进行了磁场与温度场的耦合分析,从而使得结构设计更加准确[13-14]。
本文是将磁力轴承的结构尺寸进行三维建模和优化分析,然后利用Maxwell进行电磁场分析,再利用workbench温度场耦合分析。分别模拟磁力轴承在不同结构和电流下的电磁力变化以及温度分布变化,从而对其工作状态进行预测,为结构设计提供了依据。
1 基本结构
利用磁力轴承的可控性优势,将其应用于振动控制中,进而实现在线控制。在文献[15]中对E型电磁轴承结构设计进行了说明,并且在文献[16]中对8磁极和12磁极的径向磁力轴承进行了性能对比,在电磁力和磁极间的耦合程度进行比较,得出12磁极的磁力轴承电磁性能更佳。图1所示为基于CAD模型结构示意图,表1为磁力轴承基本尺寸。
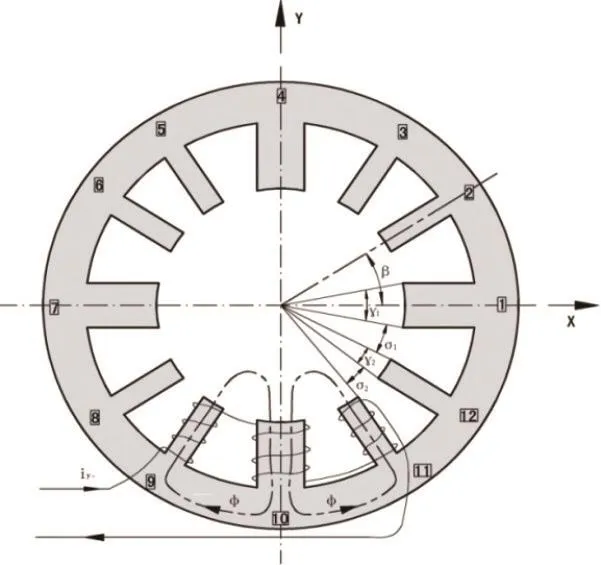
图1 基本CAD模型结构Fig.1 The basic CAD model structure

表1 磁力轴承基本尺寸Tab.1 The basic dimensions of electromagnetic bearings
2 结构优化
为了在较小体积较小电流的情况下,达到承载力为10 000N以上的目标,需要对该结构的定子外径、磁极宽度以及磁轭宽度进行优化。

图2 不同外径下电磁力与电流曲线图Fig.2 Electromagnetic force and current curve of different outer diameters
为了研究不同定子外径下的磁力轴承的变化情况,设定定子外径在370~390mm之间变化,选取电磁力较大的前三个外径分别为390mm,386mm,370mm,电磁力随时间变化曲线如图2所示。考虑磁力轴承的大小和承载力之间的关系,优选D=370mm。图3对外径为366~372mm的定子进一步分析,对电磁力进行比较,很明显观察在到370mm的外径下,电磁力更大。综合考虑两次优化过程,将磁力轴承的定子外径设定为370mm。
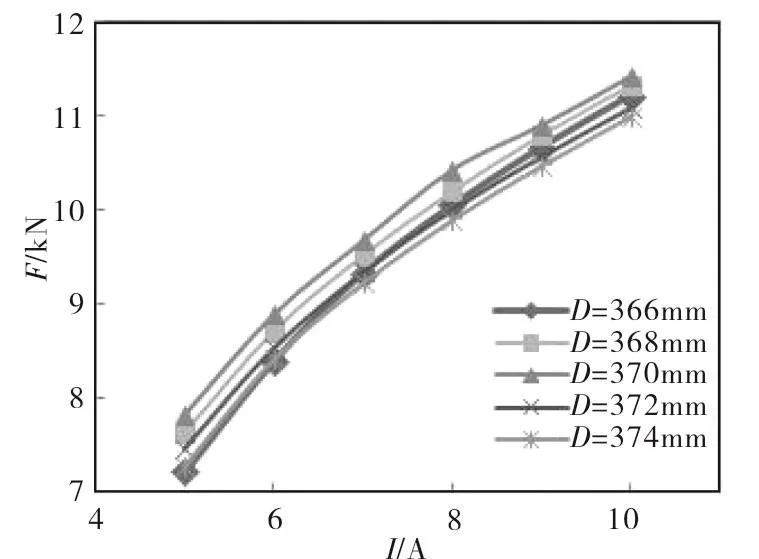
图3 不同外径下电磁力与电流曲线图Fig.3 Electromagnetic force and current curves at different external diameters
为防止磁饱和对电磁力计算准确性的影响,在分析不同磁轭厚度时,将通电电流设定为2A,磁轭宽度在20~30mm之间变化。仿真结果如图4所示,发现随着磁轭宽度的增大,电磁力并不是一直增大,而在磁轭宽度为25mm时达到最大值,因此将25mm设定为最终磁轭厚度。

图4 电磁力随磁轭宽度变化情况Fig.4 Electromagnetic force varies with the width of the magnet yoke
分析外径为370mm,定子磁轭宽度为25mm,副磁极的宽度在10~15mm之间的变化,保证主磁极的宽度为副磁极宽度的2倍,通过观察图5可以发现电磁力并不是一直增加,当该变量达到13mm以后,电磁力开始呈现下降趋势。故设定本磁力轴承的副磁极宽度为26mm。
图6为最终确定的结构,在0~10A的电流情况下优化结构的电磁力变化曲线图,可以用来指导该结构在压缩机转子稳定性监测中的应用。在通电电流达到8A后,可达到目标10 000N承载力的要求。表2中为最终优化后的结构尺寸。
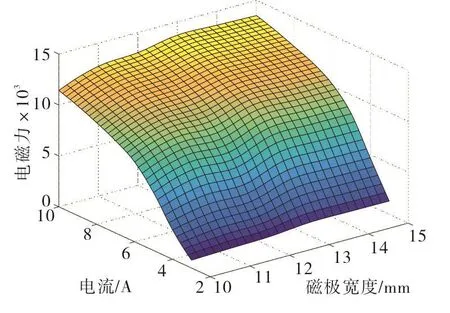
图5 电磁力随副磁极宽度变化情况Fig.5 Electromagnetic force varies with the width of the anciuary magnetic pole
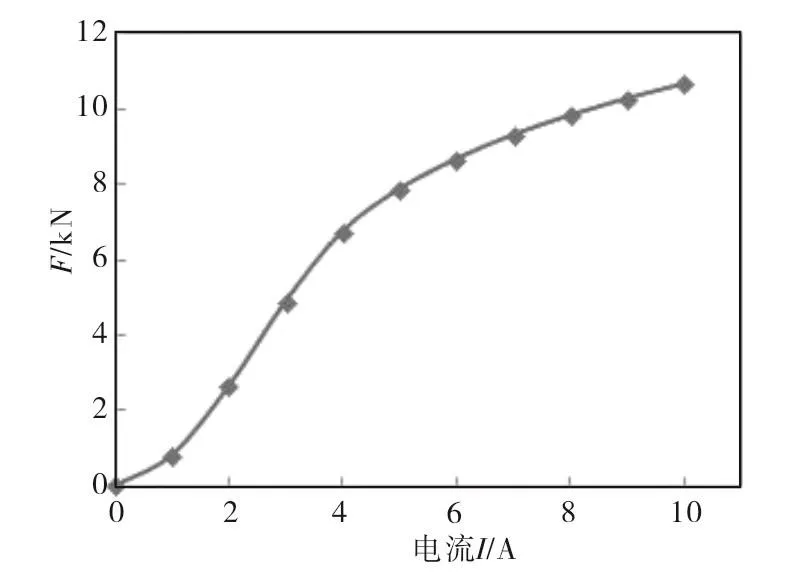
图6 最终结构下电磁力随电流变化情况Fig.6 The electromagnetic force with the electricity current changes in the final structure

表2 磁力轴承最终结构尺寸Tab.2 The final structure size of electromagnetic bearing
3 磁场-温度场耦合分析
磁力轴承工作时输入的电流包括静态偏置电流以及动态的控制电流。在分析磁力轴承损耗时,为了不忽略其控制电流,而采用谐波分析的方法。计算磁力轴承在工作中由于损耗等引起的温升变化,忽略定子绕组的涡流以及磁滞效应。
考虑到结构的对称性,在模拟时选取四分之一结构进行仿真,在仿真中,对转子和定子的截面施加对称边界条件,对线圈通入频率为不同频率的交变电流。在四分之一模型外部设置region创建计算区域,计算损耗。
利用Maxwell对磁力轴承进行损耗计算,主要包括铜损和铁损,分别计算得到各部位的损耗量,通过计算瞬态分析下各结构处损耗量,导入workbench中热量分布情况如图7所示。
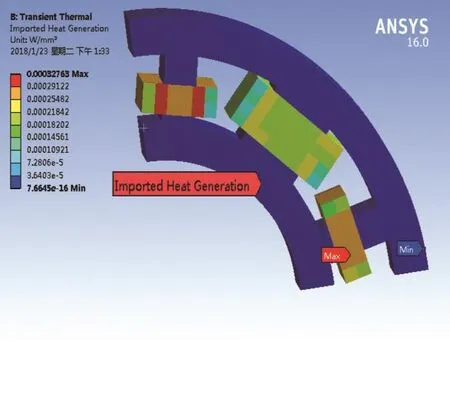
图7 各部分损耗分布图Fig.7 The loss distribution
瞬态热分析的过程中,这个系统里的温度、物体的热流率、系统的边界条件以及内能都是随时间变化而变化的。但由能量守恒和傅里叶定律可以得出,导热体内部瞬态下的热平衡微分方程表示为:
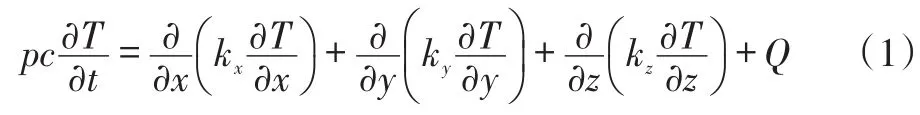
其中,T表示导热固体的温度,℃;ρ表示系统材料的密度,kg/m3;c表示系统材料的比热,J/(kg·K);t表示瞬态计算的时间,s;kx,ky,kz分别表示系统材料在x,y,z三个方向上的导热系数,W/(m·K);Q为系统内的热源在单位时间内单位体积产生的热量,J。

表3 各种材料基本性能Tab.3 The basic performance of various materials
绕组线圈是包括外层绝缘部分以及内部铜线,在三维分析中,将线圈处理为一个整体,因此需要代入等效导热系数计算公式,其中表3为各种材料基本性能:

δi,λi分别表示第i层导体的厚度以及其对应的导体导热系数。
本文计算得绕组线圈的等效导热系数为31.2W/m·℃。通过在Workbench中对磁力轴承进行瞬态热分析,设置对流换热系数、对称边界等边界条件,进行瞬态温度场仿真模拟。模拟8 000s内的温升变化,通过提取该结构在这段时间内的温度变化情况,会发现该结构的温度逐渐保持稳定。
在分析中,主要考虑定子转子和线圈的发热情况对磁轴承的温升影响。线圈产生的热量可以通过热传导,将热量传到定转子,这部分热量再通过热对流的方式传递到空气中;也可以直接进行空气热交换。对于定转子产生的热量,可直接进行热对流,将热量传递给空气,同时热辐射是在任何情况下都存在的传热方式。综上对于系统的传热方式,采用复合传热进行计算。
参考文献[17]复合传热系数计算公式为:

式中,αc表示自然对流传热系数,W/(m2·℃);αr表示辐射传热系数,W/(m2·℃)
本文复合传热系数取为9.7W/(m2·℃)
将瞬态场分析的损耗直接导入到瞬态温度场中进行分析,观察图8~10各部件温度变化,可发现工作一段时间后,温度升高幅度减缓。四分之一模型分析时,转子中间部分正对着大磁极,因此此处温度最高,越往两侧温度越低,但温度分布变化不大,可达到51.4℃以上。定子的温度变化可看出,小磁极的温度略高于大磁极,维持在67℃左右,而大磁极温度在66℃左右。

图8 转子温度场分布情况Fig.8 The temperature field distribution of the rotor

图9 定子温度场分布情况Fig.9 The temperature field distribution of the stator

图10 线圈温度场分布情况Fig.10 The temperature field distribution of the coils
4 实验分析
4.1 电磁力标定
磁力轴承实验台搭建完成后,需要首先进行电磁力的标定实验,确保装置安装的精度并能达到预期的承载能力,图11为该试验台的实物图,图12为测定电磁所需装置。

图11 实验台装置实物图Fig.11 The test rig

图12 电磁力测量实验装置Fig.12 The measurement experiment device of electromagnetic force
首先将本电磁轴承中的四个大磁极分别标记为1磁极(上),2磁极(左),3磁极(下),4磁极(右)以便后续对电磁力的记录,接下来通过塞尺方式确定定子和转子之间的间隙为0.5mm,并在实验中保持此间隙不变。实验前将测量电磁力的传感器调零处理,实验中,在0~7A范围内每次改变0.5A间隔,通过不断改变不同磁极的通电与否及通电电流大小,得到电磁力及电流的对应关系如图13所示,并作进一步分析。

图13 各磁极电磁力随电流变化情况Fig.13 Electromagnetic force of each magnet pole changes with the electricity currents
测量并记录各对不同磁极的电磁力,并进行对比分析,测量结果如图14所示,会发现各磁极电磁力随电流变化的趋势基本相近。

图14 实验值与仿真值电磁力的对比情况图Fig.14 The comparison of experimental value and simulation value of the electromagnetic force
对比实验中各磁极磁力平均值和仿真值,两条曲线的曲线大体相似,在通电电流为4A前,仿真值偏大,通电电流大于4A后,实验值偏大。由于各对磁极的间隙有些许不同,以及实验中电磁力引起的弯曲变形也会有影响。
4.2 温度实验
测温传感器选择为铂电阻(Pt100)传感器,如图15所示,该传感器的温度测量在-50℃~200℃范围内,误差不超过0.35℃。每次实验都将转速设定为3 000rpm,多次测量,如图6为大小磁极的每次实验的稳定时的温度变化情况。定子的温度在36℃附近浮动,转子的温度在30℃附近浮动。实验结果与前面仿真结果对比。仿真值普遍高于实验值。可能原因分析如下:设置线圈的电阻率略高于实际值;仿真中的对流系数和实际情况下的有偏差;加工和安装误差的存在导致结果偏差等。

图15 磁力轴承温度测量装置示意图Fig.15 Temperature measurement devices of magnetic bearings
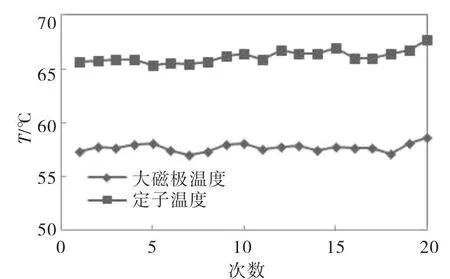
图16 不同试验次数下的温度变化情况图Fig.16 The temperature changes in different times
5 结论
通过对磁力轴承进行优化设计,确定了重载荷磁力轴承的结构。
1)外径为370mm,定子磁轭厚度为25mm,副磁极宽度设定为13mm。可以保证达到10 000N的承载力。
2)磁力轴承温度仿真中,将Maxwell计算的损耗耦合到Workbench里面进行计算,经过一定时间的计算会得到定子和转子的温度分布情况,可以进一步对结构优化进行指导。
3)对磁力轴承进行了电磁力标定实验,并与仿真值进行了比对。同时也对磁力轴承进行了温度测量实验。得出该实验台可以达到预期承载力,温度变化在可控范围内。
