深部高应力空区拱架效应与采场结构尺寸的相依性

姜立春，王玉丹，赵奎



深部高应力空区拱架效应与采场结构尺寸的相依性

姜立春1, 2，王玉丹2，赵奎3

(1. 华南理工大学 土木与交通学院，广东 广州，510640； 2. 华南理工大学 安全科学与工程研究所，广东 广州，510640； 3. 江西理工大学 资源与环境工程学院，江西 赣州，341000)

基于采场顶板围岩破坏形式，构建空区顶板岩拱力学模型；利用无铰拱理论计算岩拱内力，选取深部采场跨度及矿柱宽度等因素作为相依性分析指标，推导采场跨度()及矿柱宽度()关于拱轴系数()及拱高()的数学表达式。以某深部高应力金属矿空区为研究对象，分析采空区拱架效应与其结构尺寸(采场跨度()及矿柱宽度())依存关系，并对顶板位移进行150 d监测。研究结果表明：当一定时，随着减小而增大；当一定时，随着增大而增大；当=2，=3 m，=7 m时，矿柱合理间距为31 m；在150 d内，顶板最大位移变形在6 mm之内，未发生垮塌现象。该研究结果可为深部高应力条件下釆场结构尺寸设计提供依据。

深部开采；高应力；无铰拱；拱轴系数；采场跨度

在深部高应力作用下，岩体拱架效应是岩体内部应力为抵抗不均匀变形而进行自我调整、应力转移的一种力学现象[1−2]。充分利用岩体拱架的自承载能力，可以提高深部开采空区的稳定性。目前，国内外许多学者对地下工程中的拱架效应及深部高应力进行了研究[3−15]。TANG等[10]研究了双隧道埋深和间距与压力拱的关系，发现了1个压力拱和2个独立的压力拱成型条件；KOBATI[11]通过对隧道顶部下沉问题进行研究，发现无黏结材料拱架效应存在；BARRY等[12]提出了利用层状岩石拱减少硐室顶部变形、防控地表沉陷的机理；HUANG等[13]在研究自然平衡拱判别条件的基础上，给出了极限自稳平衡拱的椭圆曲线方程；钮新强等[14]通过对硐室围岩顶拱承载力学机理的研究，提出地下硐室岩体稳定拱存在的力学条件；李夕兵等[15]分析了在初始静载应力增大过程中，外界动力扰动对深部矿柱稳定性的影响。总体来说，既有的岩(土)体拱架效应研究很少涉及深部矿山采场尺寸(采场跨度及矿柱宽度)参数选择方面，难免造成采场维护成本高、生产效率低、矿石损失贫化率高等问题。本文作者拟通过构建岩体无铰拱力学模型，推导出高应力作用下金属矿拱架效应拱轴系数与采空区结构尺寸(采场跨度、矿柱宽度)之间的关系式，揭示采空区拱架效应自承能力与矿柱宽度及采场跨度的相依性，利用案例分析和工程校验计算结果，以便为深部开采采场结构参数设计提供依据。

1 采空区拱架效应力学模型

1.1 高应力表达式

深部高应力极易给采场布设带来危险，容易造成采场顶板冒落、底板开裂等问题[16−17]，顶板破坏形式与应力、岩性和岩体结构等密切相关。

由文献[18]并考虑岩体自重和构造应力协同作用，将采场上部的高应力简化为集中力作用在拱形顶板上(见图1)。此时，拱形顶板弯矩近似于两端固支梁弯矩分布，其基本组合一般式为

式中：为高应力和上覆岩体重力组合值；G为上覆岩体自重荷载分项系数；Q为高应力荷载分项系数；k为上覆岩体均布荷载标准值；k为高应力荷载标准值，通常取10 kN/m2。

1.2 空区拱架效应力学模型

在金属矿深部开采过程中，岩体的受力状况与浅地表的受力状况存在较大差别。围岩的切向应力集中，径向应力减小，在采空区顶拱附近产生1个环向主压应力带，应力荷载主要通过类似于拱结构作用从顶拱传到拱脚处及空区两侧围岩。因此，可将采场空区拱式顶板、间柱及周边围岩简化为一个系统，见图1。可将系统内一定厚度采空区顶板简化为无铰拱，采场跨度为，见图2(其中，和为无铰拱拱趾，为等截面圆弧无铰拱圆心)。在相邻矿块开挖后，采空区顶板竖直方向受岩体自重应力0和高地应力k作用。

图1 采空区构成简图

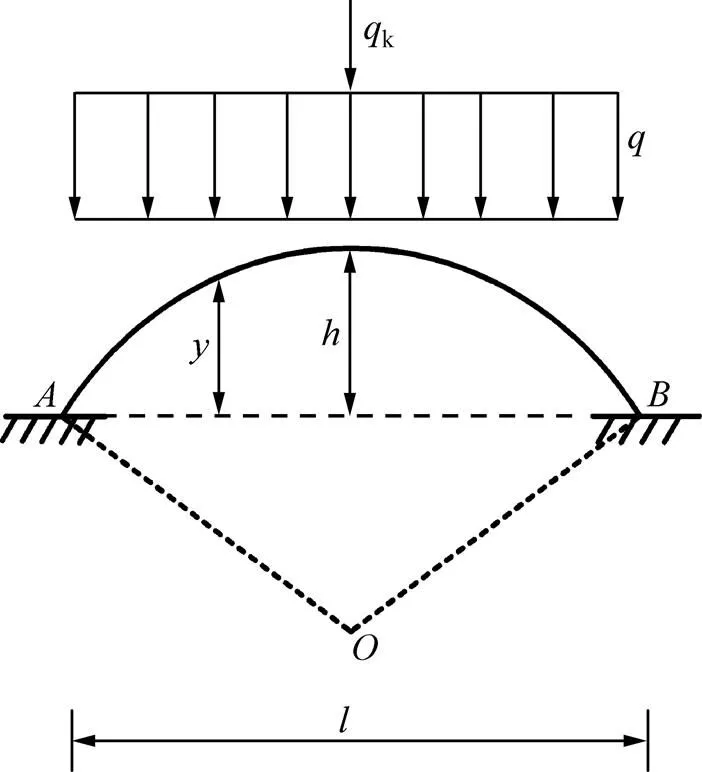
图2 无铰拱结构模型

2 釆空区拱架效应内力分析

2.1 基本假设

1) 假设相邻拱脚与矿柱接触处形成三角形受 压区。

2) 拱内力分布满足无铰拱理论，其方程为

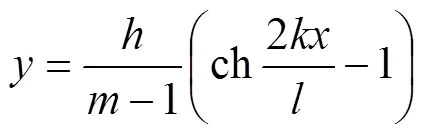
式中：为拱轴系数；为与有关的参数；为拱高；为采空区结构跨度。

3) 一定厚度的拱形顶板为等截面曲梁。拱形顶板破坏形式为张裂破坏，拱最不稳定截面在曲梁中心，此时，拱形顶板轴力和剪力对顶板影响较小，通常忽略不计。

在矿岩自重荷载和高应力作用下，顶板出现不同程度的向下位移变形；顶板上部受压应力作用，下部受拉应力作用。由于岩体的单轴抗压强度远大于其抗拉强度，顶板的破坏变形主要由拉伸破坏引起[19]。可从强度角度分析顶板的拉伸破坏。

由材料力学的弯曲梁理论可得顶板跨中截面最大弯矩(max)：

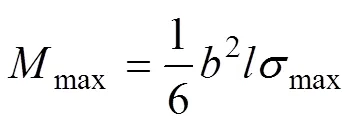
式中：max为最大弯矩；为拱圈厚度；max为顶板跨中截面弯曲时最大正应力。

由岩石强度理论知，当顶板的最大拉应力max超过其承受的拉应力阀值[]t时，即发生塑性破坏。max须满足

式中：υ为岩体完整系数；t为岩石极限抗拉强度；为安全系数，根据文献[20]，取为2.2。

2.2 拱架效应内力计算

采用力法对无铰拱结构模型进行求解。该模型有3个多余约束，为3次超静定结构。利用结构的对称性原理，选取对称的拱形顶板进行分析，在顶板中心区域虚拟截开，取拱顶的弯矩1、轴力2及剪力3为多余未知力，见图3。

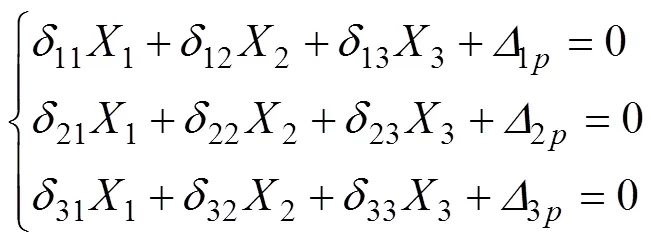
由叠加法可得模型顶板任意截面所受弯矩的表达式为

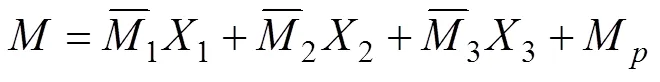
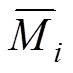
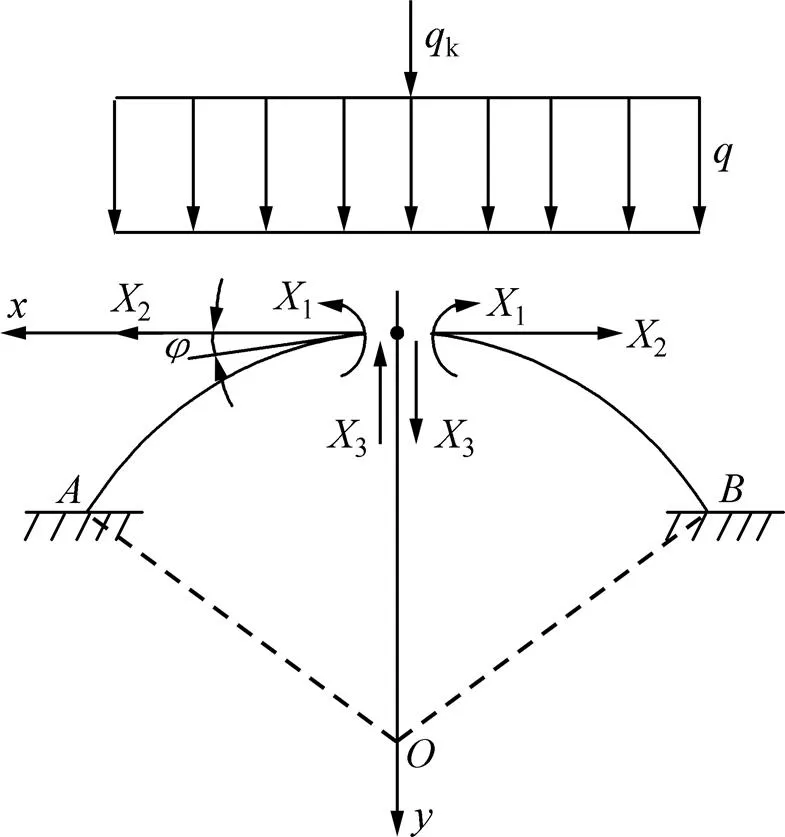
图3 基本体系

由积分方法，求得力法方程(式(5))中的系数和自由项，可求得多余未知力1和2的表达式：

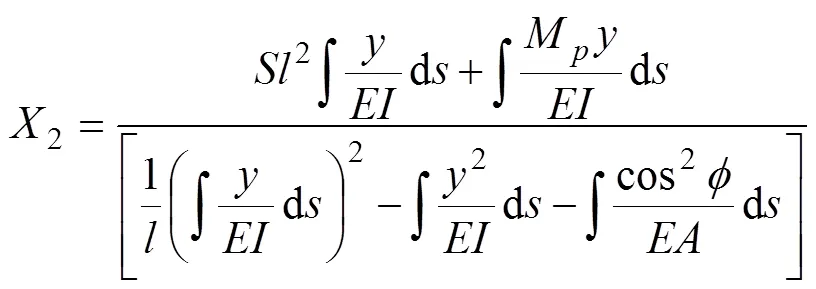
式中：为拱形顶板任意截面的纵坐标；为曲梁上任意点切线与轴之间的夹角；为岩体弹性模量；为拱形顶板截面面积；为拱形顶板截面惯性矩。

在高应力及岩体自重荷载作用下，顶板岩体上部受压应力作用，下部受拉应力作用。由于岩体的单轴抗压强度远大于其抗拉强度，顶板的变形主要有拉伸破坏引起。根据结构力学方法，将式(7)和(8)代入式(6)可得()：

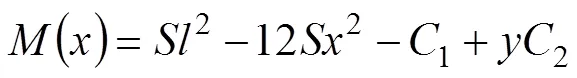
式中：为拱形顶板任意截面的横坐标；为拱形顶板任意截面的纵坐标；1=1；2=2。

在高应力作用下，拱形顶板弯矩分布形式近似于两端固支梁弯矩分布形式，顶板中部发生应力集中，最大弯矩max出现在顶板围岩的中心区域位置。对()求极值可得：

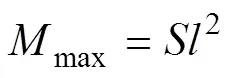
式中：max为拱形顶板计算截面最大弯矩；为采场跨度。

2.3 采空区拱架效应因素影响

深部釆空区拱架效应表现为岩体最大限度地发挥抗剪强度、调节内部应力分布，其形状在宏观上反映了拱的受力特征。根据采空区顶板破坏形式，影响釆空区拱架效应主要因素有釆深、采场结构参数(如采场跨度、釆厚、矿柱宽度、采场布置)、推进速度等。经分析，矿柱顶端与拱脚接触面形成三角形受压区，见 图4。

图4 拱圈厚度与矿柱宽度之间的关系图

图4所示为拱圈厚度与矿柱宽度之间关系图。由图4可知在△中，拱圈厚度()与矿柱宽度()之间的关系为

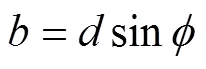
式中：为矿柱宽度；为拱形顶板切线与轴之间的夹角。

同样，可求得拱形顶板拱圈厚度为

2.3.1 矿柱宽度对空区拱架效应的影响

文献[21]中的密度试验结果表明，矿柱宽度变化对拱圈厚度影响最显著，矿柱宽度与拱圈厚度成正比。将式(10)和(12)代入式(3)可得矿柱宽度的表达式：

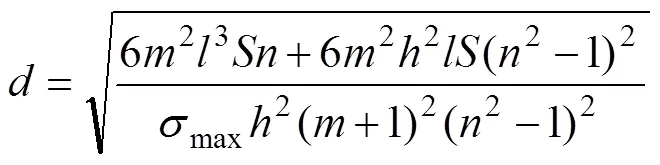
2.3.2 空区结构跨度对空区拱架效应影响

深部开采时，若釆场跨度过小，则采空区拱架效应若对周边围岩无约束作用，造成矿石损失贫化；若釆场跨度过大，则拱形顶板拱内岩体抗弯强度大于极限抗弯强度，可能导致顶板垮塌，增加采场维护成本。当拱的高度和跨度一定时，拱的形状主要取决于拱轴系数()。随着增大，采场跨度()逐渐增加，拱的形状随之不断改变。因此，由式(3)，(10)，(12)和(13)可得采场跨度()与拱轴系数()之间的数学表达式：

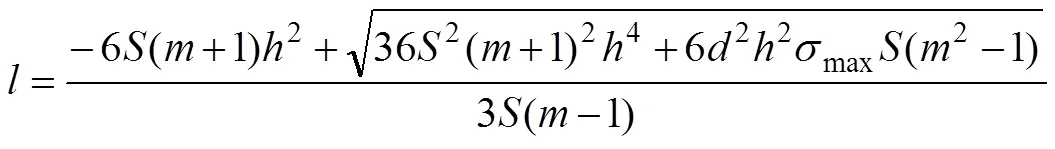
3 案例分析

3.1 工程概况

某铜矿山为超深高地应力矿山，现釆深度为 1 237 m，主要采矿方法为空场嗣后充填法，生产能力为300万t/a。矿床属层控矽卡岩型铜矿床，矿体位于青山背斜轴部，赋存于石炭系黄龙组和船山组层位中，呈似层状产出；顶板为大理岩，底板主要为粉砂岩和石英闪长岩。矿山部分岩体物理力学参数如表1所示。受深部高应力的影响，矿柱宽度及采场结构跨度设计不合理，采场经常发生垮塌问题，影响采场安全及铜矿石回收率。

这里利用深部岩体原生结构拱架效应自承能力和采空区自稳定机理，分析矿柱宽度及采场跨度随着拱轴系数变化规律，以便为矿山采场参数设计提供依据。

表1 岩体物理力学参数

3.2 结果分析

3.2.1 矿柱宽度与采空区拱架效应相依性分析

在常规应力条件下，当采空区结构跨度分别为 10 m和20 m时，矿柱宽度与采空区拱轴系数的关系见图5。由图5可知：矿柱宽度随着拱轴系数的增加而增大，变化曲率逐渐减小。

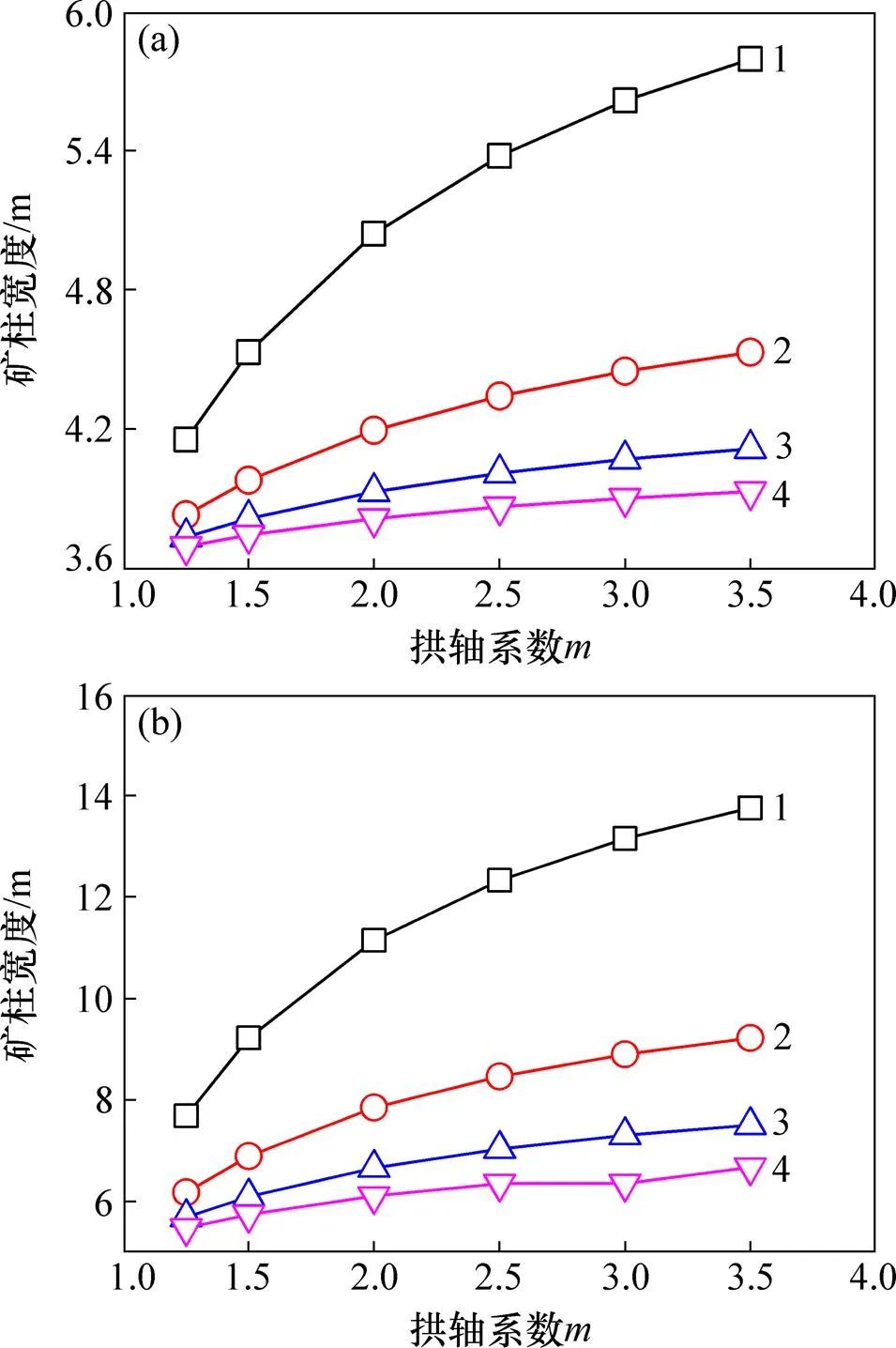
采场跨度l /m：(a) 10；(b) 20

在高应力条件下，由式(13)可得采空区拱架形状()与矿柱宽度()之间的关系。图6所示为在高应力作用下，当采空区结构跨度分别为10 m和20 m时，矿柱宽度与采空区拱轴系数的关系。由图6可知：在深部开采高应力作用下，矿柱宽度()随着拱轴系数()增加而增大，变化曲率逐渐减小。

分析图5和图6可知：在常规应力和高应力条件下，矿柱宽度随着拱轴系数变化趋势相似；当其他条件一定时，与高应力和常规应力相比，矿柱最小允许宽度增加；当=3.5，=20 m，=3 m时，在常规应力下，矿柱宽度=13.76 m；在高应力下，矿柱允许宽度=15.09 m，最小允许宽度增加8.81%。其原因为：在浅部开采时，顶板仅承受上覆岩体自重应力；在深部开采时，采场顶板除承受上覆岩体自重应力外，还受高应力作用，此时，顶板形成的塑性区明显增大，应力更加集中。为了回采安全，矿柱最小允许宽度相应增加。

采场跨度l /m：(a) 10；(b) 20

3.2.2 采空区结构跨度与拱架效应相依性分析

图7所示为常规应力作用下，当矿柱宽度为5 m和8 m时，采空区跨度()与采空区拱轴系数()关系。分析图7可知：随着拱随着拱轴系数()的减小，采场跨度()逐渐降低；随着增大，逐渐递增加。

由式(14)可得高应力作用下采空区拱架形状()与采空区结构跨度()之间的关系。当矿柱宽度为5 m和8 m时，采场跨度()与采空区拱轴系数()关系见图8。分析图8可知：在深部高应力作用下，釆场跨度()随着拱轴系数()减小逐渐增加；随着增加逐渐 减小。

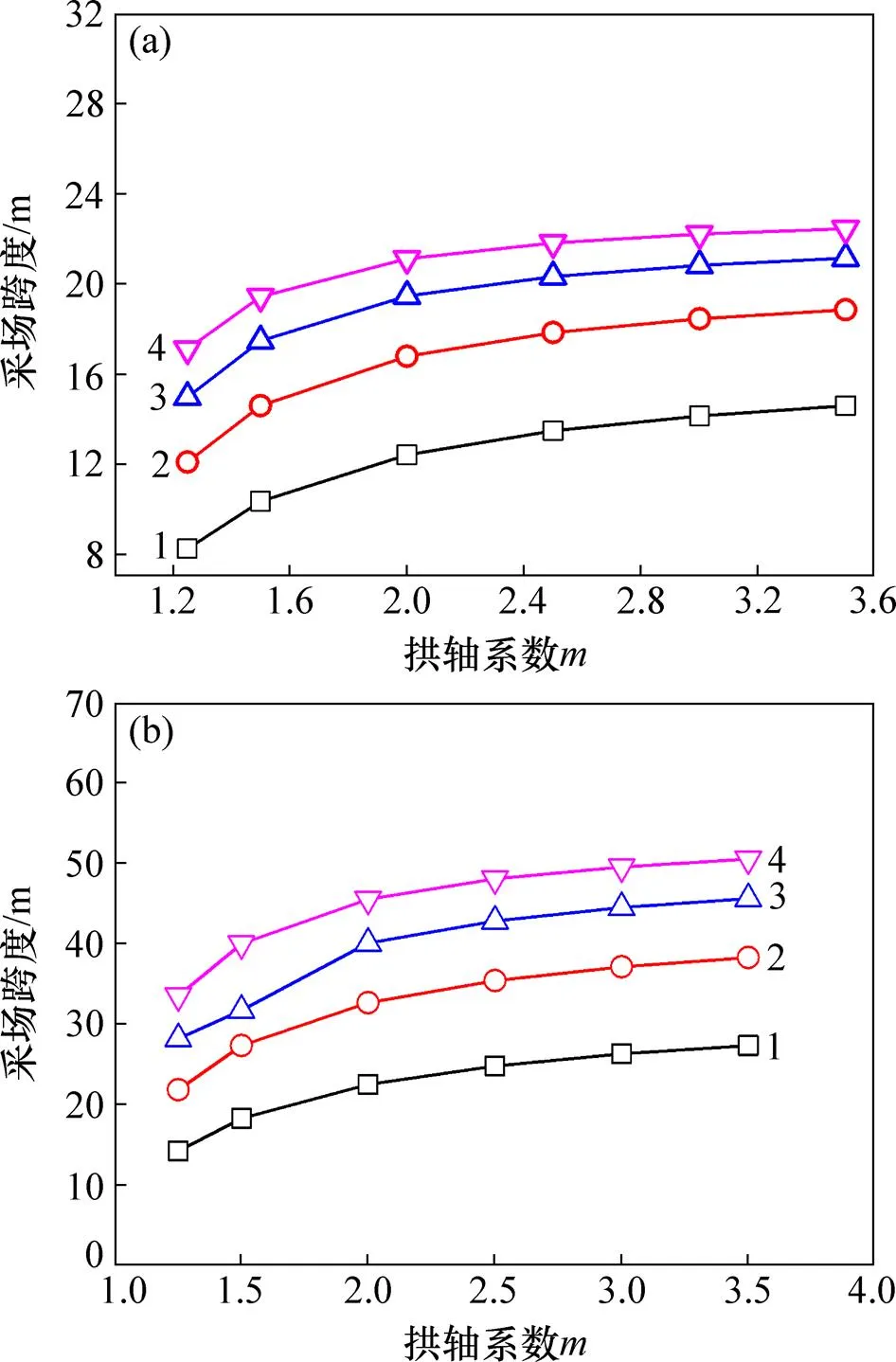
矿柱跨度d/m：(a) 5；(b) 8

分析图7和图8可知：在高应力和常规应力条件下，采场跨度随着拱轴系数变化趋势相反，在高应力下，采场跨度()随着拱轴系数()增大而减小；在常规应力条件下，采场跨度()随着拱轴系数()增大而增加；当=3.5，=8 m，=3 m时，在常规应力下，采场允许最大跨度=27.32 m；在高应力下，采场最大允许跨度=34.95 m，最大允许跨度增加21.83%。其原因为：在高应力作用下，采场顶板发生应力集中现象；随着采场跨度增大，顶板应力趋于集中；顶板(无铰拱结构)上部岩层压应力增大，下部岩层拉应力逐渐增大，拉应力分布范围逐渐扩大，采空区顶板岩层受拉伸剪切范围扩大。因此，为了确保采场安全，在高应力条件下，采场跨度应随着拱轴系数增大而减小。

经综合分析可知：在深部高应力作用下，当拱轴系数()趋近于0时，拱轴线趋近直线，岩拱效应对周边围岩约束作用消失，采场跨度应取极大值max；当拱轴系数()增大到一定值时，拱内拉裂变形增大，拱内岩体抗弯强度达到极限抗弯强度，拱形顶板达到极限承载力，采场跨度应取极小值min。

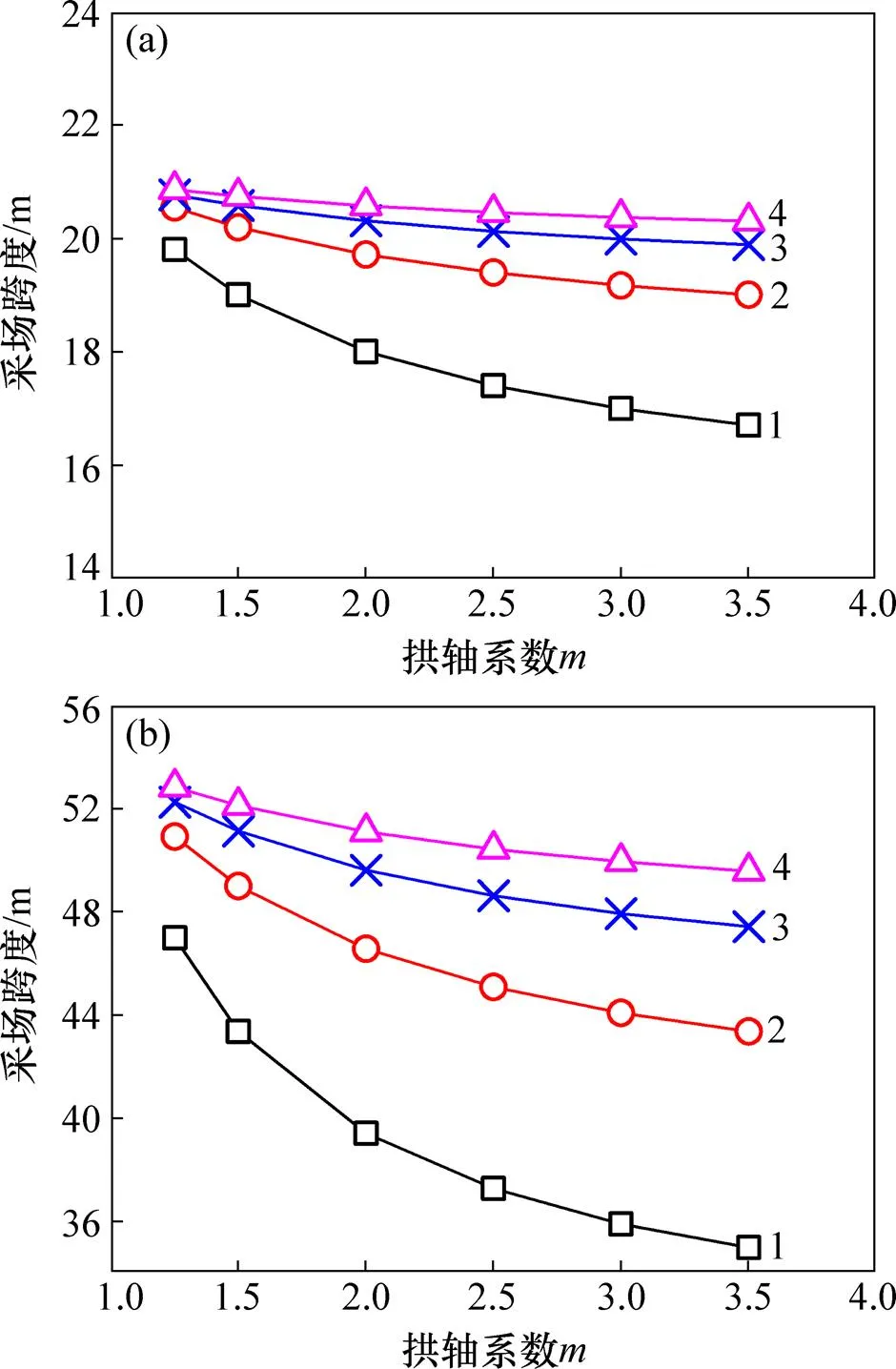
矿柱跨度d/m：(a) 5；(b) 8

因此，在深部开采过程中，综合开采效率和安全等因素，采场合理跨度应在min和max之间。

3.3 工程应用

为了充分开釆埋深铜矿体，保证釆准作业安全及采空区顶板围岩的稳定性，在回采矿体时，采场以拱形形状进行推进。采场设计拱轴系数=2，矿柱宽度=7 m，拱高=3 m，由式(14)及案例分析可得矿柱合理间距()为31.81 m。因此，设计采场跨度取31 m。

为了观测采场顶部位移变化情况，对采矿后的2个空区顶板沉降位移进行监测，观测点分别位于2个采场顶板中心区域。150 d位移监测结果表明：采场顶板最大位移变形不超过6 mm(见图9)，没有发生局部塌陷现象(见图10)，拱架效应约束作用明显，验证了理论分析结果的可靠性。

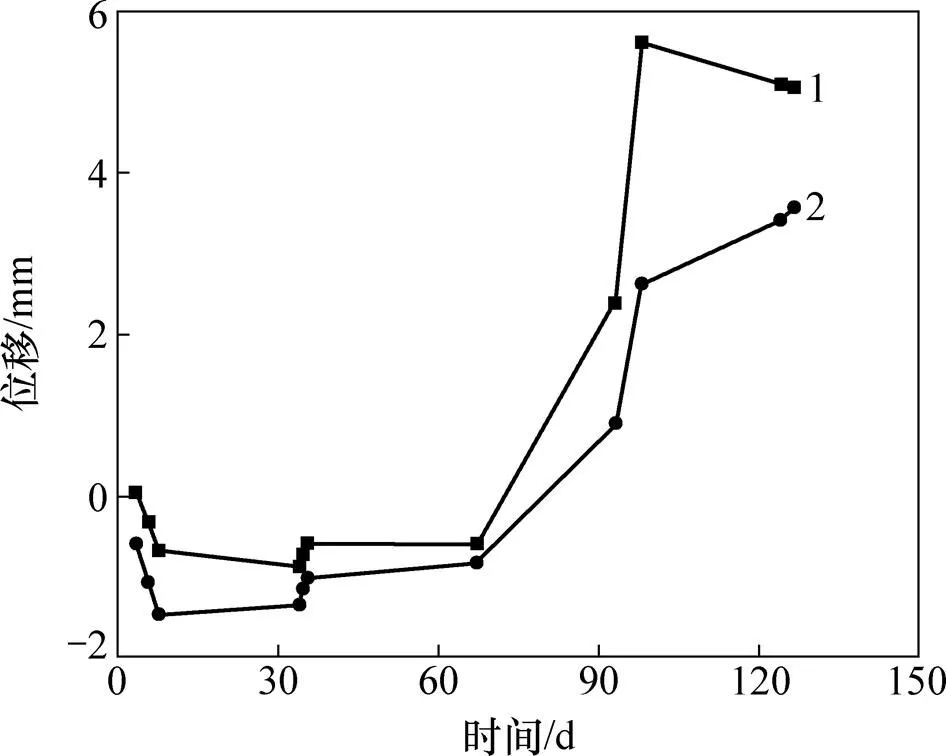
1—监测点1；2—监测点2。

图10 回采结束采场顶板实景

4 结论

1) 基于深部高应力下顶板围岩破坏特征，构建了采空区顶板岩拱力学模型。采用无铰拱理论计算岩拱内力，分析了采空区拱架效应与其结构尺寸的相依性。

2) 在分析影响深部高应力条件下空区拱架效应主要因素的基础上，选取采场跨度()及矿柱宽度()等主控结构参数，作为采空区拱架效应及其结构尺寸相依性分析指标，推导出深部采场跨度()及矿柱宽度()关于拱轴系数()及拱高()的数学表达式。

3) 以某大型深部高应力金属矿采场结构为研究对象，分析了采空区拱架效应与采场跨度()及矿柱宽度()等主要结构尺寸的依存关系。当矿柱宽度一定时，采场跨度()随着拱轴系数()的减小而递增；当采场跨度一定时，矿柱宽度()随着拱轴系数()的增加而递增。在高应力作用下，矿柱最大允许宽度增加10.67%，采场最大允许跨度增加21.83%。

4)当拱轴系数=2，拱高=3 m，矿柱宽度=7 m时，矿柱合理间距为31 m。2个采场顶板150 d的最大位移变形在6 mm之内，没有发生垮塌现象，采场顶板安全状态良好，空区顶板岩体拱架效应约束作用明显。

[1] 向欣, 王义峰, 孟国涛, 等.大跨度地下洞室拱顶稳定性及支护措施研究[J].岩石力学与工程学报, 2012, 31(增刊): 3643−3649.XIANG Xin, WANG Yifeng, MENG Guotao, etal.Study of stability and supporting measures of chamber arch crown for large span underground caverns[J].Chinese Journal of Rock Mechanics and Engineering, 2012, 31(Suppl): 3643−3649.

[2] 姜立春, 曾俊佳, 吴爱祥.水平采空区群动力响应的类非线性振动模型[J].中南大学学报(自然科学版),2017, 48(6): 1577−1584.JIANG Lichun, ZENG Junjia, WU Aixiang. A similar nonlinear vibration model for dynamic responses of horizontal goaf group[J]. Journal of Central South University(Science and Technology), 2017,48(6): 1577−1584.

[3] 江军生, 曹平. 深部高应力下层状岩体巷道底鼓机理及控制技术[J]. 中南大学学报(自然科学版), 2015, 46(11): 4218−4224.JIANG Junsheng,CAO Ping.Floor heaving mechanism of soft rock in high-stress deep roadway and its control technology[J].Journal of Central South University (Science and Technology),2015, 46(11):4218−4224.

[4] 江权, 冯夏庭, 陈国庆, 等. 高地应力条件下大型地下洞室群稳定性综合研究[J]. 岩石力学与工程学报, 2008, 27(增2): 3768−3777. JIANG Quan, FENG Xiating, CHEN Guoqing, et al. Stability study of large underground caverns under high geostress[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(Suppl 2): 3768−3777.

[5] 郑康成, 丁文其, 金威. 基于模型试验与FEM的TBM圆形隧道压力拱成拱规律[J]. 煤炭学报, 2015, 40(6): 1270−1274. ZHENG Kangcheng, DING Wenqi, JIN Wei. Formation law of pressure arch of circular TBM tunnel based on model test and FEM[J]. Journal of China Society, 2015, 40(6): 1270−1274.

[6] 贺广零, 黎都春, 翟志文, 等. 采空区顶板塌陷破坏的力学分析[J]. 石河子大学学报(自然科学版), 2007, 25(1): 104−108. HE Guangling, LI Duchun, ZHAI Zhiwen, et al. Analysis of failure and instability of stiff roof[J]. Journal of Shihezi University (Natural Science), 2007, 25(1): 104−108.

[7] 梁晓丹, 刘刚, 赵坚.地下工程压力拱拱体的确定与成拱分析[J].河海大学学报(自然科学版), 2005, 33(3): 315−317. LIANG Xiaodan, LIU Gang, ZHAO Jian. Definition and analysis of arching action in underground rock engineering[J]. Journal of Hehai University(Natural Sciences), 2005, 33(3): 315−317.

[8] 宋义敏, 潘一山, 章梦涛, 等. 深部高应力载荷作用下的洞室变形破坏试验[J]. 辽宁工程技术大学学报(自然科学版), 2008, 27(4): 489−491. SONG Yimin, PAN Yishan, ZHANG Mengtao, et al. Experimental study on deformation failure of deep rock mass under high stress load[J]. Journal of Liaoning Technical University (Natural Science), 2008, 27(4): 489−491.

[9] 顾金才, 顾雷雨, 陈安敏, 等. 深部开挖洞室围岩分层断裂破坏机制模型试验研究[J]. 岩石力学与工程学报, 2008, 27(3): 433−437. GU Jincai, GU Leiyu, CHEN Anmin, et al. Model test study on mechanism of layered fracture within surrounding rock of tunnels in deep stratum[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(3): 433−437.

[10] TANG CA, THAM LG, LEE PKK, et al.Numerical studies of the influence of microstructure on rock failure in uniaxial compression. Part I: effect of heterogeneity[J].International Journal of Rock Mechanics and Mining Sciences, 2000, 37(4): 555−569.

[11] KOBATI K. Erroneous concepts behind the new Austrian tunnelling method[J].Tunnels and Tunnelling, 1994(11): 38−41.

[12] BARRY HG, BROWNE T.Rock mechanics for underground mining[M].London:George Allen and Unwin, 1985: 212−213.

[13] HUANG Z, BROCH E, LUM. Cavern roofstability-mechanism of arching and stabilization by rockbolting[J].Tunnelling and Underground Space Technology, 2002, 17(3): 249−261.

[14] 钮新强, 丁秀丽.地下洞室围岩顶拱承载力学机制及稳定拱设计方法[J].岩石力学与工程学报, 2013, 32(4): 776−786.NIU Xinqiang, DING Xiuli.Bearing mechanism of top arch and stable arch design method for surrounding rock of underground caverns[J].Chinese Journal of Rock Mechanics and Engineering, 2013, 32(4): 776−786.

[15] 李夕兵, 李地元, 郭雷, 等.动力扰动下深部高应力矿柱力学响应研究[J].岩石力学与工程学报, 2007, 26(5): 923−928.LI Xibing, LI Diyuan, GUO Lei, et al.Study on mechanical response of highly-stressed pillars in deep mining under dynamic disturbance[J].Chinese Journal of Rock Mechanics and Engineering, 2007, 26(5): 923−928.

[16] 张海波, 宋卫东, 付建新. 大跨度空区顶板失稳临界参数及稳定性分析[J]. 采矿与安全工程学报, 2014, 31(1): 67−71. ZHANG Haibo, SONG Weidong, FU Jianxin. Analysis of large-span goaf roof instability critical parameters and stability[J]. Journal of Mining & Safety Engineering, 2014, 31(1): 67−71.

[17] 王金安, 李大钟, 马海涛, 等.采空区矿柱−顶板体系流变力学模型研究[J].岩石力学与工程学报, 2010,29(3): 578−582.WANG Jinan, LI Dazhong, MA Haitao, et al.Study of rheological mechanical model of pillar-roof system in mined−out area[J].Chinses Journal of Rock Mechanics and Engineering, 2010, 29(3): 578−582.

[18] 梁宁, 伍法权, 王云峰, 等.大埋深高地应力关山隧道围岩变形破坏分析[J].岩土力学, 2016, 37(增刊2): 330−336. LIANG Ning, WU Faquan, WANG Yunfeng, et al. Analysis of deformation and failure of rock mass of deep Guanshan Tunnel under high in situ stress[J]. Rock and Soil Mechanics, 2016, 37(Suppl 2): 330−336.

[19] 杨宇江, 高晗, 李元辉. 附加荷载作用下空区顶板稳定性分析[J]. 东北大学学报(自然科学版), 2011, 32(9): 1332−1335. YANG Yujiang, GAO Han, LI Yuanhui. Analysis on roof stability of concealed gob area under additional loading[J]. Journal of Northeastern University(Natural Science), 2011, 32(9): 1332−1335.

[20] 赵延林, 吴启红, 王卫军, 等.基于突变理论的采空区重叠顶板稳定性强度折减法及应用[J].岩石力学与工程学报, 2010, 29(7): 1425−1434.ZHAO Yanlin, WU Qihong, WANG Weijun, et al.Strength reduction method to study stability of goaf overlapping roof based on catastrophe theory[J].Chinese Journal of Rock Mechanic and Engineering, 2010, 29(7): 1425−1434.

[21] 张敏思, 朱万成, 侯召松, 等.空区顶板安全厚度和临界跨度确定的数值模拟[J].采矿与安全工程学报, 2012, 29(4): 544−548.ZHANG Minsi, ZHU Wancheng, HOU Zhaosong, etal. Numerical simulation for determining the safe roof thickness and critical goaf span[J].Journal of Mining & Safety Engineering, 2012, 29(4): 544−548.

(编辑 陈灿华)

Dependence between goaf arching effect and its structure size under high stress

JIANG Lichun1, 2, WANG Yudan2, ZHAO Kui3

(1. School of Civil Engineering and Transportation, South China University of Technology, Guangzhou 510640,China； 2. Institute of Safety Science and Engineering, South China University of Technology, Guangzhou 510640,China； 3. Faculty of Resource and Environmental Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China)

Based on the analysis of the destroying of surrounding rock of the roof, a roof-arch and rock-mechanical model was built. The internal force was calculated by fixed end arch algorithm. Deep mining goaf pillar width span structure and other factors were selected as dependency analysis index, and expressions of span() and pillar width() related to coefficient of arch axle() and height() of arch were deduced. Taking large metal deep mine under high stress of the stope as the object, relationship between goaf arch effect and structure size(and) was analyzed. The roof displacements were monitored in 150 d. The results show that whenis definite,decreases with the decrease of. Whenis definite,increases with the increase of. The reasonable pillar spacing is 31 m when=2,=3 m and=7 m. The max roof displacement deformation is less than 6 mm, and no collapse happens, while the stope of roof is safe during 150 d.It is reasonable to design a goaf structure under high stress at deep mine.

deeping mining; high stress; hingeless arch; arch axis coefficient; pillar spacing

10.11817/j.issn.1672−7207.2018.10.026

TD 853

A

1672−7207(2018)10−2576−08

2017−11−12；

2018−01−08

国家重点研发计划项目(2016YFC0600802)；国家自然科学基金资助项目(51174093，51364012) (Project(2016YFC0600802) supported by the State Key Research Development Program of China; Projects(51174093, 51364012) supported by the National Natural Science Foundation of China)

姜立春，博士，教授，从事矿山岩土安全研究；E-mail：ginger@scut.edu.cn