非均质地基中V−T联合受荷桩承载力分析

邹新军，夏尉桓，王亚雄



非均质地基中−联合受荷桩承载力分析

邹新军，夏尉桓，王亚雄

(湖南大学 土木工程学院，湖南 长沙，410082)

为研究非均质地基中单桩基础在桩顶竖向力()和扭矩()联合作用下的承载特性，假定桩侧地基土剪切模量和极限侧摩阻力沿深度呈指数函数非线性增加，并考虑桩−土接触面上位移的非协调性，根据剪切位移法和桩身荷载传递函数建立桩身位移控制方程，引入相应的力和位移边界条件，导出桩周土体处于理想弹性和塑性受力状态时的桩身内力位移解答，由此求得不同桩顶载荷工况(不同−组合与加载顺序)下的桩身承载力及其包络线。在此基础上，进一步采用ABAQUS对−联合受荷桩进行数值模拟对比分析，获得不同工况下的桩身破坏机理、影响桩身承载力的关键因素及其规律。研究结果表明：桩身承载力随桩身长径比的增大而增大，但随桩土刚度比的增大而逐渐减小；桩顶可承受的竖向力(扭矩)随扭矩(竖向力)增加不断减小而趋于零。

桩基础；−联合荷载；非均质地基；荷载传递函数；数值分析

随着我国基础设施建设的不断推进特别是近海资源的持续性开发，城市立体交通的弯梁桥、跨海大桥、海上风力发电塔等结构物不断兴建。为满足上部结构对基础的承载力、变形及稳定性等方面的要求，这类结构物多采用桩基础，但由于其所处环境复杂，除承受竖向力()、水平力()和弯矩()外，还可能承受不可忽视的扭矩()作用。常规设计方法难以考虑这种复杂受荷工况，不能合理地评价桩身极限承载力，导致设计偏于不安全，因此，对于这类复杂受力环境中的桩基础设计，应考虑，，或的联合作用。已有研究者对−[1]，−[2]和−−等组合进行了研究，但很少考虑扭矩的共同作用。鉴于问题的复杂性，本文先探讨−联合受荷桩的承载特性。人们对单一竖向受荷桩的承载变形分析进行了系统研究，如：GUO[3]考虑桩−土接触面位移非协调并视桩周土为Gibson地基，采用荷载传递法和剪切位移法得到桩身内力位移解析解；RAJAPAKSE[4]假定桩周土体剪切模量随深度呈线性变化，使用积分变换法推导出桩基的弹性理论解。目前，一些学者对纯受扭桩进行了研究，如：RAJAPKSE[5]引入变分法将桩和土分解为柱形杆件及单独的弹性土体，并使用Green函数表示应力和位移的关系，然后采用Hankel积分变换求得其数值解；陈胜立等[6]基于传递矩阵法和积分变换导出了成层地基的位移解，并根据桩−土位移协调条件导出桩身受扭问题的半解析解；孔令刚等[7]建立了群桩扭转非线性分析模型，用Mindlin解模拟桩−土相互作用，引入经验性耦合系数，分析了桩侧地基土抗力对桩身扭转承载力的影响；邹新军等[8−9]视桩周土剪切模量随深度分别呈指数和幂函数分布，并考虑单层和双层地基，导出桩侧土分别处于不同受力状态时桩顶的扭矩−扭转角解析解。目前，人们对于−联合荷载桩的承载变形特性的研究较少。GEORGIADIS等[10−11]将桩身视为弹性杆，以相互作用的非线性轴向弹簧与扭转弹簧模拟桩周土的约束作用，采用传递矩阵法编制出相应计算程序，该法模型简单，但计算复杂，且不能考虑桩−土接触面位移非协调性。邹新军等[12]视桩周土为Gibson地基，考虑了竖向力和扭矩不同大小组合与加载顺序，并考虑桩−土接触面上位移的非协调性，导出了桩周土分别处于弹、塑性状态时的桩身内力位移解答。综上所述，有关−联合荷载桩的承载特性研究仍有待深入。为此，本文作者基于已有研究成果，以剪切模量随深度呈指数函数增加来模拟地基的非均质特性，考虑桩−土接触面上的位移非协调和−不同组合与加载顺序等因素，基于剪切位移法和荷载传递函数建立桩身位移控制方程，进而推导桩身内力位移解答。在此基础上，基于ABAQUS进行数值模拟对比分析，进一步探讨−联合受荷桩的破坏机理及其承载力的关键影响参数与规律。

1 竖向受荷桩与受扭桩分析

鉴于问题的复杂性，为简化分析，进行如下假定。

1) 视桩身为理想弹性体，桩周土为非均质地基，即假定桩侧地基土剪切模量和桩侧极限摩阻力f随深度均按下式呈指数函数模式增加(见图1)：

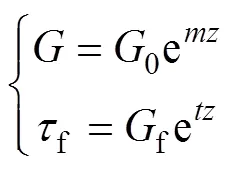
式中：为深度(m)；0和f分别为桩侧土体剪切模量(MPa)和极限摩阻力的分布常数(MPa)；和为非线性系数(m−1)，=/；为土层厚度(m)；为非负的量纲一常数，取决于上覆土层的特性(可由试验确定)，=0时表示土层为均质土。的取值与的取值相同。

2) 桩周土处于弹性受力阶段时桩−土位移协调，进入塑性阶段后桩−土接触面可局部相对滑移。

3) 任一深度处的桩侧摩阻力服从理想弹塑性模型，即该深度处的摩阻力线性增加至极限摩阻力后保持不变，且该极限值随深度按式(1)变化。

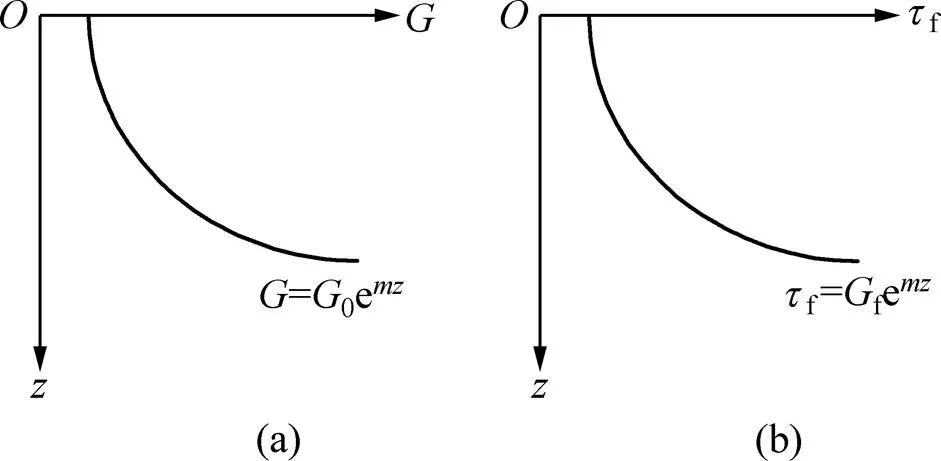
(a) 剪切模量分布模型；(b) 极限摩阻力分布模型

1.1 非均质地基中竖向受荷桩分析

当桩顶仅作用竖向力且桩周土处于弹性受力状态时，由桩身微元体的力平衡条件等可建立桩身位移控制方程：

式中：vz为桩侧摩阻力(kPa)；p和p分别为桩身的截面积(m2)和材料弹性模量(kPa)；为桩径(m)；()为深度处的桩身截面位移(m)。

引入RANDOLPH等[13]导出的桩−土接触面上的摩阻力与位移间的关系式：

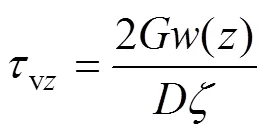
式中：0为桩身半径(m)；m为影响半径(m)，m=2.5(1−)；为土体泊松比，为桩长(m)；为/2深度处与桩底处土的剪切模量之比；()为桩−土接触面上土体的竖向位移(m)；为轴向荷载传递因 子[13]。

考虑桩−土位移协调即()=()，将式(1)，(3)及(4)代入式(2)可得

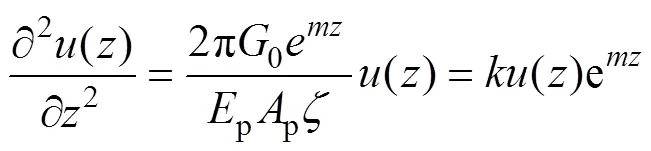
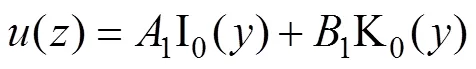
桩身截面上的轴力与位移关系式如下：

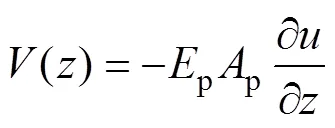
将式(6)代入式(7)可得

式中：I1(•)和K1(•)分别为第一类和第二类变型Bessel函数。

分别用b与b表示桩底处的轴力和位移，并引入桩底处力与位移的边界条件：

再引入Randolph和Wroth关于桩底处b与b­的关系式[14]：

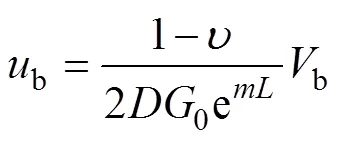
联立式(6)，(8)和(10)，解得待定系数1和1：

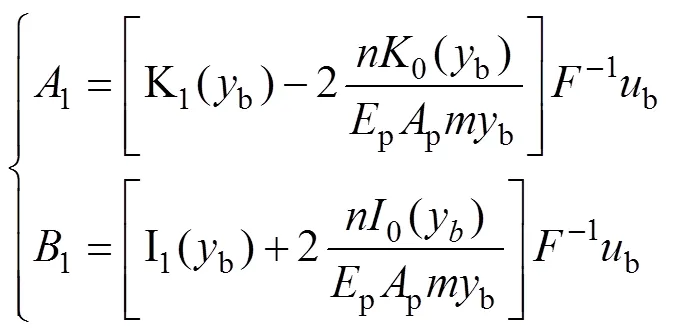
将式(11)分别代入式(6)和(8)可得

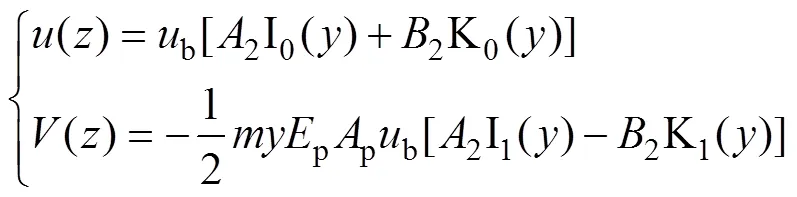
其中：21b；B=B1b。

不断增加桩顶竖向力，直至出现桩−土相对滑移后，假定达到t时桩−土相对滑移点已发展至深度v1处。为求解此时的桩顶竖向位移t和v1处桩身轴力e及位移e，取桩顶至v1处的桩段为研究对象，由竖向位移连续与力平衡条件可得桩顶竖向力t及位移t：

v1处桩土位移协调即e=e，联立式(1)和(3)得

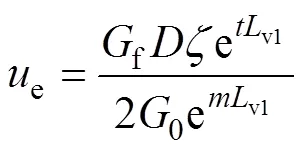
由式(12)可得v1处桩身轴力为

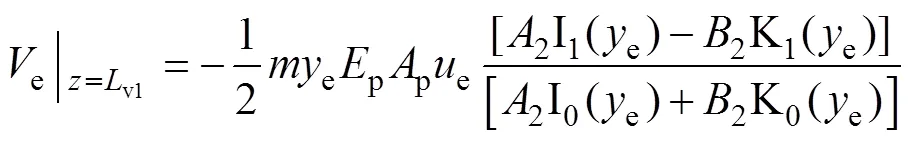
1.2 非均质地基中受扭桩分析

桩顶仅作用扭矩且桩周土处于弹性状态时，由桩身微元体力平衡条件等可建立桩身扭转控制方程：

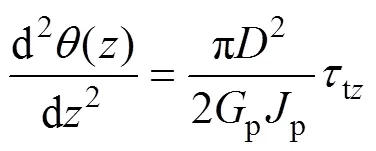
式中：()与tz分别为深度处桩身的扭转角 (rad)和环向切应力(kPa)；pp为桩身抗扭刚度(kN·m2)。

引入纯受扭桩桩−土接触面上的土体环向切应力tz与转角的关系式：

则式(16)可变为

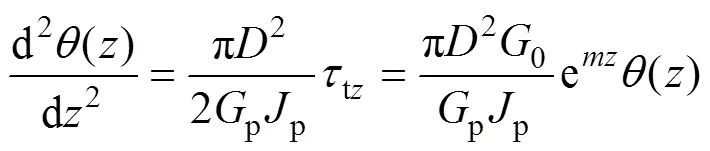
由参数变换将式(18)转为修正Bessel函数后可得

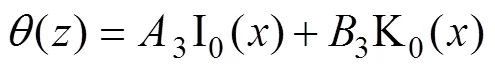
桩身任意截面处的扭矩与扭转角存在如下关系：

式中：()为深度为处桩身扭矩(kN·m)。

将式(19)代入式(20)后得()表达式：

而桩底处的扭转边界条件为

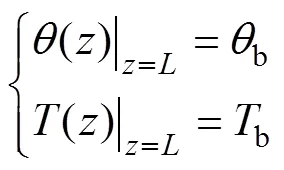
式中：b与b分别为桩底截面的扭矩和扭转角，

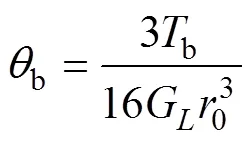
其中：G为桩底处土体的剪切模量(kPa)。联立式(19)，(21)和(23)可得

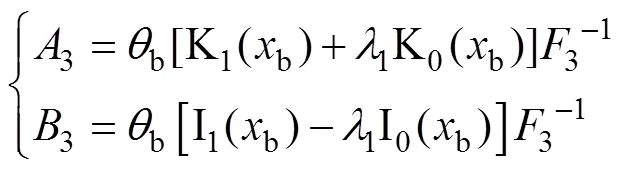
将式(24)分别代入式(19)和(21)可得

其中：43b；43b。

不断增大桩顶扭矩，直至出现桩−土相对滑移为止。假定达t时桩−土相对滑移开展至某一深度t1处，为求解此时的桩顶扭转角t及t1处的桩身扭矩e与扭转角e，以桩顶至t1处桩段为研究对象，由力平衡与扭转位移连续条件可得

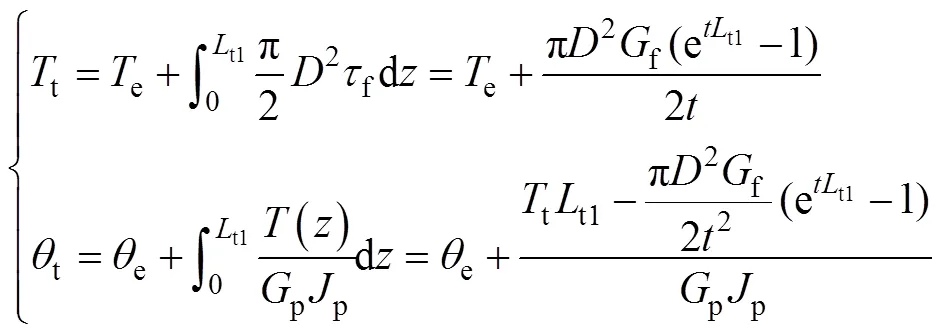
联立式(1)和(17)可得

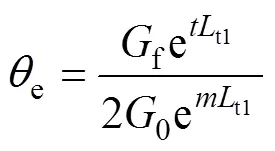
由式(25)可求得t1处的桩身扭矩为

2 不同加载顺序下V−T受荷桩分析

在桩顶−联合作用下，假定深度处桩周土体对桩身的剪切力τ可分解为竖向侧摩阻力vz与环向切应力tz(如图2所示)，且满足

2.1 弹性→弹塑性阶段

当桩顶先作用竖向力t(或扭矩t)且桩侧地基土尚处于弹性阶段时，再施加t(或t)。当t(或t)很小时，土体仍处于弹性状态，可分别按式(12)和式(25)求解桩身内力(轴力、扭矩)及变形(位移、转角)；随t(或t)增加(如图3所示)，地基土开始进入塑性阶段，假定桩−土临界滑移点距桩顶v3(或t3)，并将将该截面的内力与位移分别记为e(或e)和e(或e)。

当加载顺序为时，根据式(29)及前述解答可求得桩侧土体剪切应力为

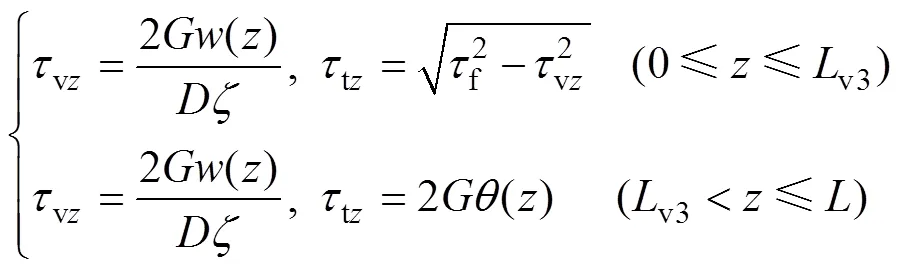
取桩顶至v3处的桩段为分析对象，根据平衡原理与位移协调条件，可求得桩顶扭矩t为

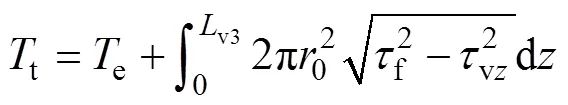
当加载顺序变为时，桩侧土体剪切应力为

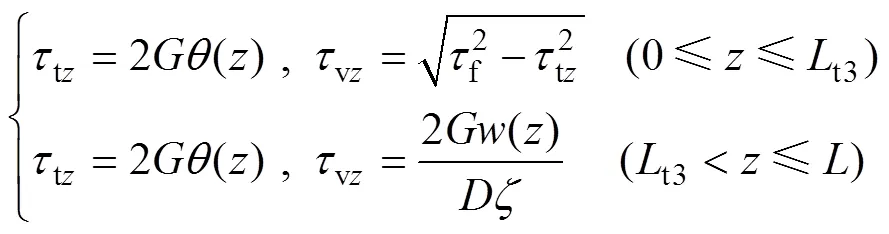
同理，取桩顶至t3处的桩段为分析对象，可求得桩顶的竖向力t为

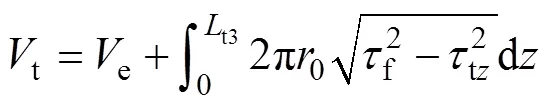
从弹性到弹塑性阶段，无论是加载还是加载，随着2种荷载组合(t，t)的增加，临界滑动点由地表逐渐发展到桩底，桩周土体由部分进入塑性到全部进入塑性，此时对应的t(t)即为桩在承受一定竖向力t(扭矩t)下所能承受的极限扭矩(竖向力)，不同的(t,t)即构成承载力包络线。

2.2 弹塑性→弹塑性阶段

当加载顺序为，桩顶作用较大竖向力t且桩周土已部分处于塑性状态(相应桩−土临界滑移点距桩顶v1)时，再施加扭矩t，则临界滑移点将从v1继续向下发展至v2处(见图4)，该截面扭矩与扭转角仍表示为e和e。

由式(28)及前述解答可求得桩侧土体剪切应力：

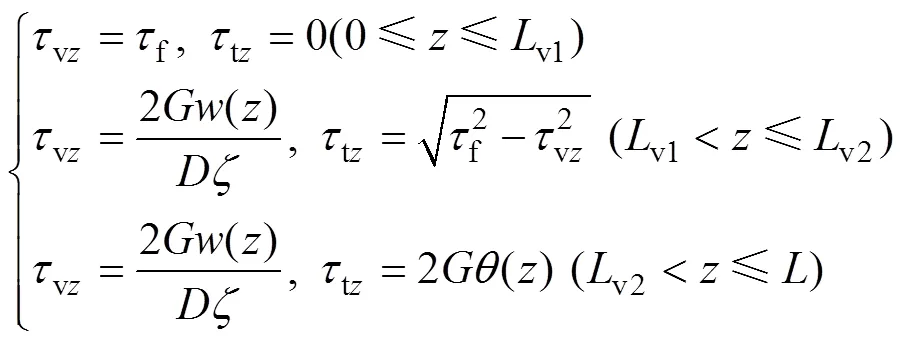
取桩顶至v2处的桩段为分析对象，根据力平衡与位移协调条件，可求得桩顶扭矩t：

当加载顺序变为时，桩顶受到较大扭矩t且桩周土已部分处于塑性状态(相应桩−土临界滑移点距桩顶t1)后，再施加竖向力t，则临界滑移点从t1继续向下发展至t2处(见图4)，该截面竖向力与沉降表示为e和e。同理可求得桩侧土体剪切应力为

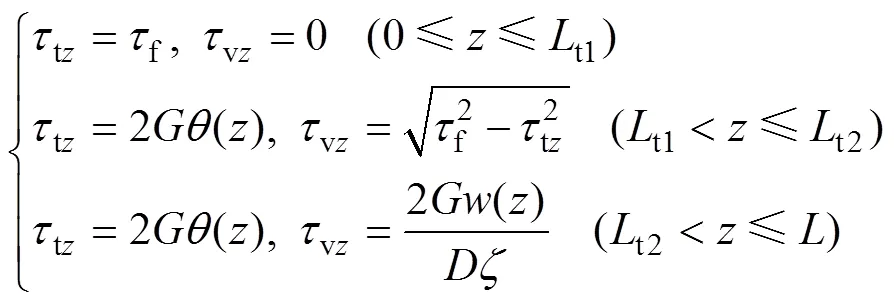
取桩顶至t2处的桩段为分析对象，根据力平衡与位移协调条件，可求得桩顶竖向力：

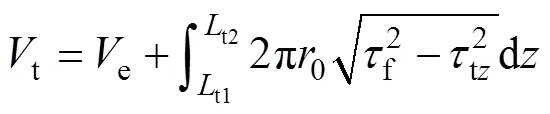
同样，从弹塑性到弹塑性阶段，对和这2种加载顺序，随着2种荷载组合(t，t)的增加，临界滑动点由v1(t1)处发展至桩底，桩周土全处于塑性阶段，此时，对应的t(t)即为桩在承受一定竖向力t(扭矩t)下所能承受的极限扭矩(竖向力)，不同(t，t)即可构成承载力包络线。

3 方法验证与参数分析

3.1 方法验证

为验证上述解答，利用文献[15]和[16]中的模型试验结果验证单一竖向受荷桩与纯受扭桩解答；在此基础上，再与文献[11]和[12]中给出的−联合受荷桩试验结果与理论结果进行对比。

对于单一竖向受荷桩，计算参数取值如表1所示。

表1 竖向受荷桩计算参数

文献[15]中模型桩竖向承载力为0.338 MN，本文计算值为0.314 MN，相对误差为7.1%。

对于纯受扭桩，取文献[16]中的2根模型桩扭转试验结果进行对比。计算参数按文献[17]中方法确定，其中，桩身抗扭刚度为12.8 MN∙m2，和分别取 2.00 m−1和0.25 m−1，其余主要参数见表2。

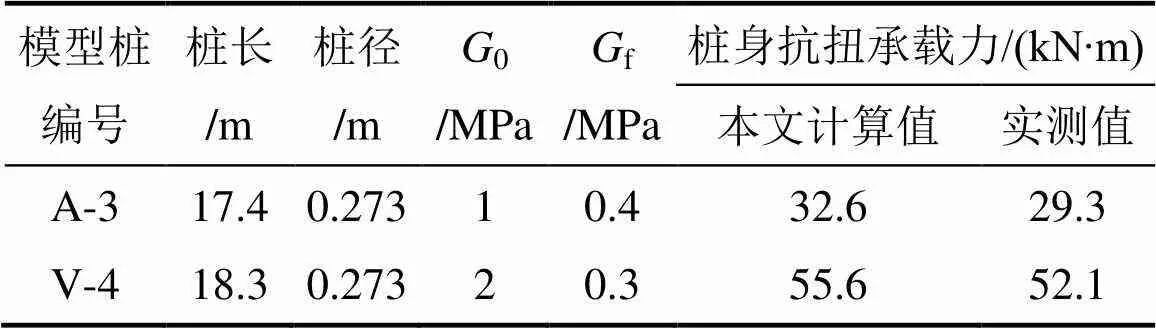
表2 纯受扭桩计算参数与结果

由表2可知：由本文解答求得的桩身扭矩承载力均略高于模型试验值。其原因主要在于假定的式(1)模型难以完全符合文献[16]中模型桩的桩周土质条件，此外，一些其他复杂试验条件也不能予以考虑。

对于−联合受荷桩，将本文计算结果与文献[11]中的试验结果、理论结果以及文献[12]中的计算值进行对比。采用的桩土参数如表3所示。桩顶先作用扭矩1.5 N∙m，后施加竖向力。

表3 V−T联合受荷桩计算参数

桩顶在承受一定扭矩情况下竖向荷载与沉降的关系曲线见图5。从图5可知：按本文方法获得的荷载位移曲线变化规律与4根模型桩的实测曲线有一定的相似性，由此确定的−联合受荷桩的竖向承载力约为174.5 N，与文献[11]中的理论计算值(约186.5 N)相对误差约为6.4%，与文献[12]中的计算值(约 165.2 N)相对误差约为5.6%。文献[12]假定桩侧地基土剪切模量和极限侧摩阻力均随深度线性增加，而本文采用指数函数模型，且本文的计算结果均值略高于文献[12]中的值。另外，文献[11]中4根模型桩试验结果具有一定的离散性，并与其理论计算值有一定差异，相比而言，本文计算结果位于试验散点最大值与最小值之间，并与文献[11]中结果更接近。

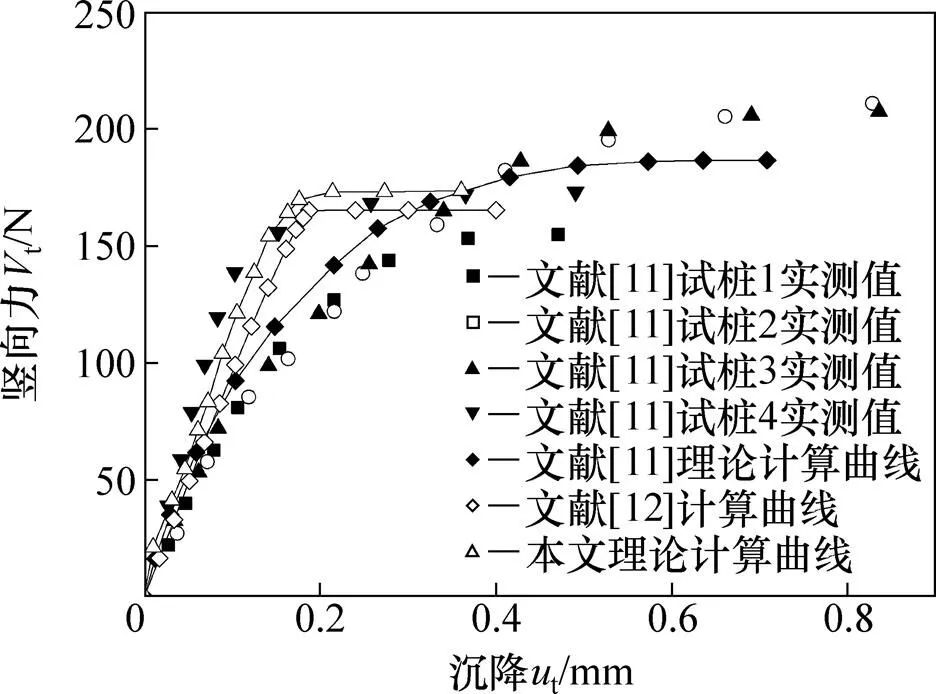
图5 V−T联合受荷桩桩顶竖向力−位移对比分析

3.2 参数分析

为了进一步探讨影响−联合受荷桩承载力的关键参数与规律，进一步基于ABAQUS进行数值模拟对比分析。

为验证模型的正确性，与文献[11]中算例进行对比分析，结果如表4所示。从表4可见：基于ABAQUS的桩身竖向承载力数值分析结果与理论计算值较吻合。

表4 基于ABAQUS的分析模型验证

在上述可行性验证的基础上，进一步对参数进行分析。模型土体计算参数(见表5)如下：弹性模量为5 GPa，泊松比为0.35，剪胀角为0°，内摩擦角为5°。黏聚力由相应深度处的土体抗剪强度反算得到。

模型分析简图和基于ABAQUS的有限元网格划分如图6所示。

表5 8号试桩计算参数

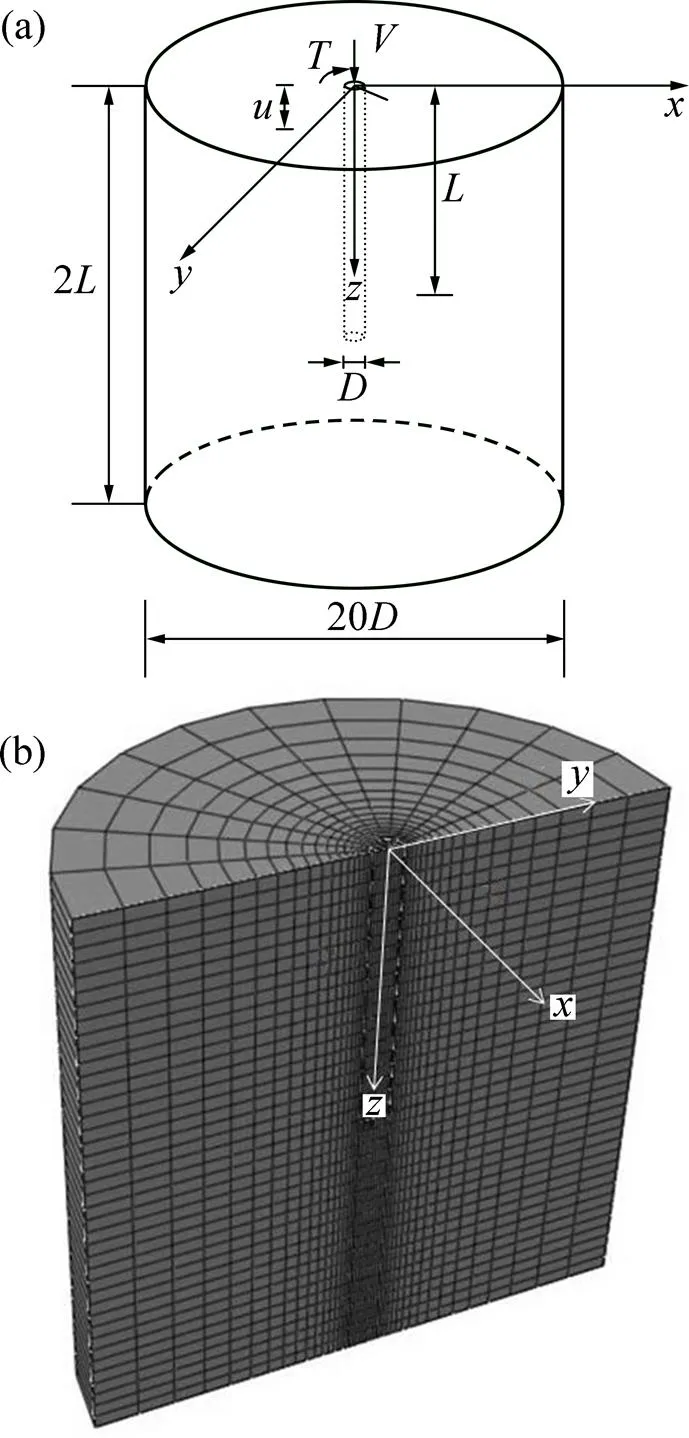
(a) 模型简图；(b) 有限元网格

经对比分析，为消除模型边界效应，模型中土体的直径为桩径的20倍，深度为桩长的2倍。桩身视为弹性体，土体破坏服从摩尔库仑准则。桩−土接触面采用hard-contact。将桩顶受力面耦合在一起，并选用圆心作为其参考点，荷载施加于该参考点上。模型边界约束条件如下：两侧约束−平面上的位移，底部约束各个方向的位移。单元类型均为C3D8R，桩身和地基土体单元数量分别为1 800个和18 480个。

取较常见的桩身长径比在10~50范围内的5个代表值和不同加载顺序进行对比分析，得到相应的桩顶竖向力t与扭矩t，如图7所示。从图7可见：随增大，桩身承载力逐渐增加，承载力包络线呈现外扩趋势，且对应的桩身承载力包络线始终位于加载时包络线的外侧。

为探讨桩土刚度比对承载力的影响，采用6组不同获得其桩顶竖向力与扭矩，相应的桩身承载力包络线如图8所示。从图8可见：随增加，桩身承载力的包络线呈收缩趋势而减小。

为获得量纲一化承载力包络线，以桩径比为10的桩为例，分析得到其最大竖向承载力为1 220 kN，最大承载扭矩为1 104 kN∙m。当竖向荷载为1 195.6 kN时，可以得到相应的极限承载扭矩为176.64 kN∙m，此时位移比/()=2(其中：为桩顶沉降，为桩顶扭转角)，将桩顶荷载量纲一化，改变桩顶荷载组合，−联合荷载下的破坏包络线如图9所示。

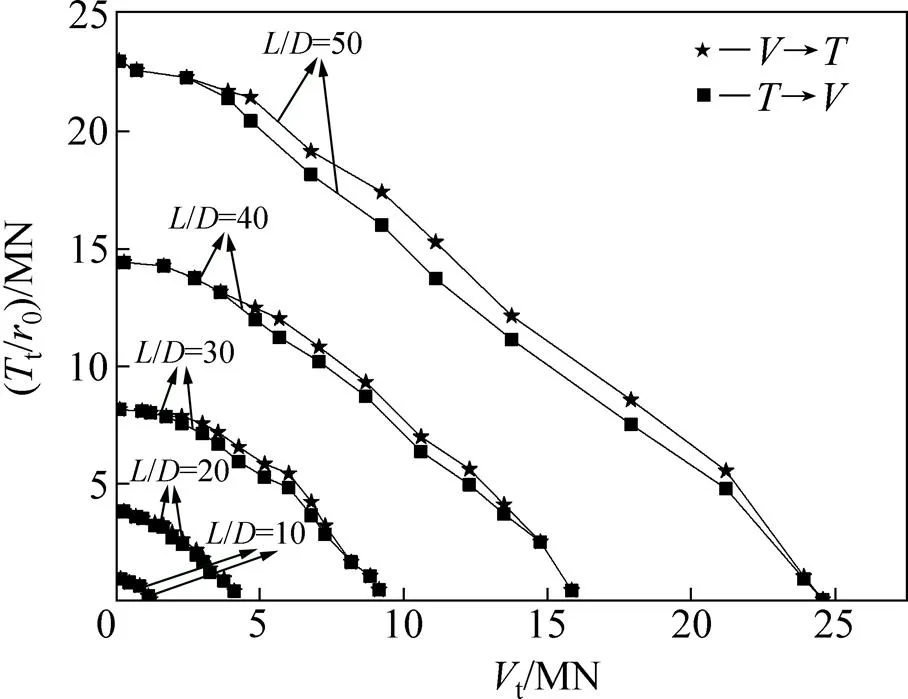
图7 长径比L/D和加载顺序对桩顶承载力包络线的影响

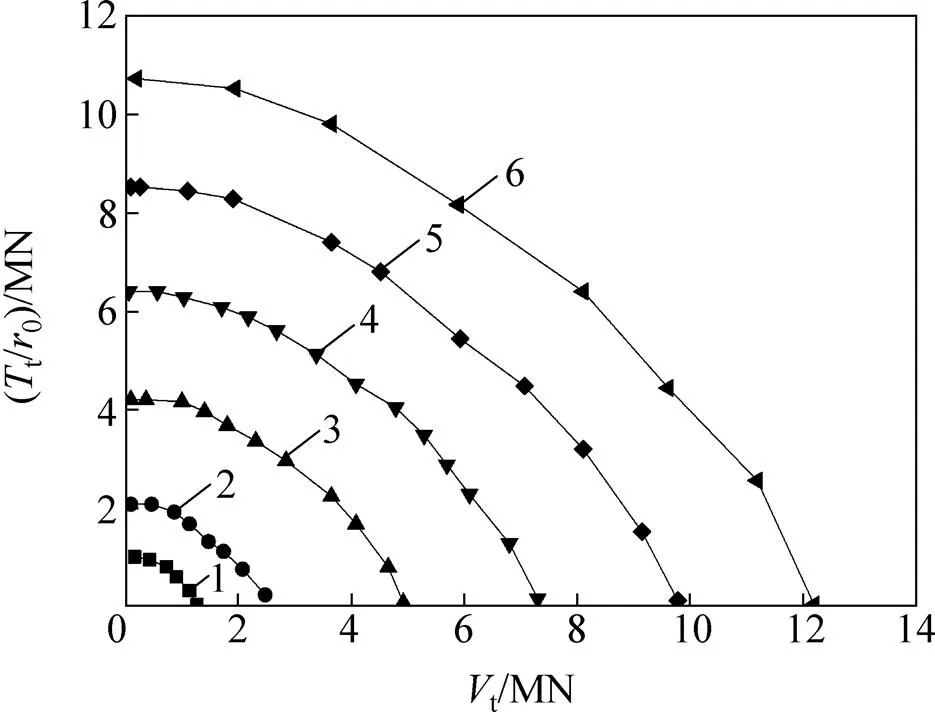
λ：1—5 000；2—2 500；3—1 250；4—850； 5—600；6—500。

图7~9表明：在上述参数的变化范围内，对于−联合受荷桩，随桩顶扭矩增加，桩顶所能承受的竖向荷载逐渐减小，且减幅呈现先大后小的趋势，但最终趋于零。

相比于单一受荷桩，−联合受荷桩的破坏主要由地基土强度破坏引起；同时，随扭矩荷载增加，桩身破坏模式由单一竖向受荷时的刺入式破坏逐渐转变为扭转剪切破坏，此时桩周土应力较大，桩底有一定刺入，桩底土形成滑动面，出现剪切破坏。

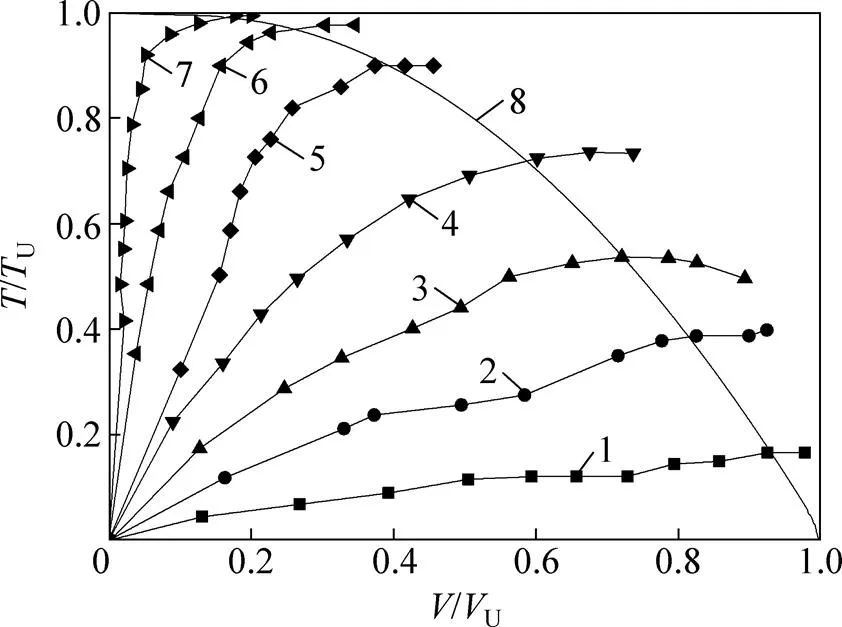
1—u/(Dθ)=2.00；2—u/(Dθ)=1.00；3—u/(Dθ)=0.75； 4—u/(Dθ)=0.50；5—u/(Dθ)=0.30；6—u/(Dθ)=0.25； 7—u/Dθ=0.10；8—包络线。

4 结论

1) 采用剪切位移法和桩身荷载传递函数建立不同−加载顺序下的桩身位移控制方程，并引入相应边界条件后，导出桩侧土分别处于弹性或弹塑性时的桩身内力位移解答。

2) 通过与已有理论与模型试验结果的对比分析，验证了所给出的单一竖向受荷桩、纯受扭桩以及−联合受荷桩的内力位移解答的合理性。

3) 桩身承载力随增大而增大，但随的增大而逐渐减小。

鉴于问题的复杂性，文中的解答及相关结论有待更深入地进行理论研究与试验验证。

[1] 邹新军, 赵明华, 邬宝林. 成层地基中倾斜受荷群桩的非线性有限元分析[J]. 中南大学学报(自然科学版), 2006, 37(4): 820−825. ZOU Xinjun, ZHAO Minghua, WU Baolin. Nonlinear finite element analysis of pile group under inclined loads in stratified subgrade[J]. Journal of Central South University(Science and Technology), 2006, 37(4): 820−825.

[2] 陈仁朋, 郑中, 孔令刚, 等. 水平及扭转荷载作用下群桩基础受力分析方法[J]. 岩土工程学报, 2013, 35(8): 1463−1469. CHEN Renpeng, ZHENG Zhong, KONG Linggang, et al. Analysis method for pile groups subjected to lateral and torsional loads[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(8): 1463−1469.

[3] GUO Weidong. Vertically loaded single piles in Gibson soil[J]. Journal of Geotechnical Engineering and Geoenvironmental Engineering, ASCE, 2000, 126(2): 189−193.

[4] RAJAPAKSE R K. Response of an axially loaded elastic pile in a Gibson soil[J]. Geotechnique, 1990, 40(2): 237−249.

[5] RAJAPAKSE R. A torsion load transfer problem for a class of non-homogenous elastic solids[J]. International Journal of Solids and Structures, 1988, 24(2): 139−151.

[6] 陈胜立, 张利民. 层状地基中单桩的扭转变形分析[J]. 岩土工程学报, 2005, 27(5): 531−534.CHEN Shengli, ZHANG Limin. Torsional response of single pile embedded in layered ground[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(5): 531−535.

[7] 孔令刚, 张利民. 群桩扭转非线性模型[J]. 岩土力学, 2009, 30(8): 2231−2236. KONG Linggang, ZHANG Limin. Nonlinear analysis of pile groups subjected to torsion[J]. Rock and Soil Mechanics, 2009, 30(8): 2231−2236.

[8] 邹新军, 徐洞斌, 王亚雄. 成层地基中单桩受扭弹塑性分析[J]. 湖南大学学报(自然科学版), 2014, 41(9): 72−78.ZOU Xinjun, XU Dongbin, WANG Yaxiong. Elastic-plastic analysis of torsional single pile in layered subsoil[J]. Journal of Hunan University (Natural Sciences), 2014, 41(9): 72−78.

[9] 邹新军, 赵灵杰, 徐洞斌, 等. 双层非均质地基中单桩受扭弹塑性分析[J]. 岩土工程学报, 2016, 38(5): 828−836.ZOU Xinjun, ZHAO Lingjie, XU Dongbin, et al. Elastic-plastic torsional behavior of single pile in double-layered non-homogeneous subsoil[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(5): 828−836.

[10] GEORGIADIS M. Interaction between torsional and axial pile response[J]. Numerical and Analytical Methods in Geomechanics, 1987, 11(6): 645−650.

[11] GEORGIADIS M, SAFLEKOU S. Piles under axial and torsion loads[J]. Computers and Geotechnics, 1990, 9(4): 291−305.

[12] 邹新军, 王亚雄, 徐洞斌. 弯梁桥中−联合受荷桩承载力分析[J]. 中国公路学报, 2015, 28(10): 51−58. ZOU Xinjun, WANG Yaxiong, XU Dongbin. Bearing capacity analysis of−combined loaded piles in curved girder bridges[J]. China Journal of Highway and Transport, 2015, 22(10): 51−58.

[13] RANDOLPH M F, WROTH C P. Analysis of deformation of vertically loaded piles[J]. Journal of Geotechnical Engineering Division, ASCE, 1978, 104(12): 1465−1488.

[14] RANDOLPH M F, WROTH C P. An Analysis of the vertical deformation of pile groups[J]. Geotechnique, 1979, 29(4): 423−439.

[15] 江杰, 黄茂松, 顾倩燕. 非均质地基中群桩竖向荷载沉降关系分析[J]. 岩土力学, 2008, 29(8): 2092−2096. JIANG Jie, HUANG Maosong, GU Qianyan. Analysis of settlements of vertically loaded pile groups in non-homogeneous soil[J]. Rock and Soil Mechanics, 2008, 29(8): 2092−2096.

[16] STOLL U W. Torque shear test of cylindrical friction piles[J]. Civil Engineering, ASCE, 1972, 42(4): 63−64.

[17] GUO Weidong, RANDOLPH M F. Torsional piles in non-homogeneous media[J]. Computers and Geotechnics, 1996, 19(4): 265−2.

(编辑 陈灿华)

Bearing capacity analysis of a single pile under combined−Loads in non-homogeneous subsoil

ZOU Xinjun, XIA Weihuan, WANG Yaxiong

(College of Civil Engineering, Hunan University, Changsha 410082, China)

To discuss the bearing behavior of a single pile under combined loading of vertical forceand torsionin non-homogeneous subsoil, the control equation of the pile shaft was set up by using the pile shaft load transferring function and shear displacement method, in which the exponential function model was adopted to simulate the increasing change of subsoil shear modulus and ultimate side resistance with depth, and the non-coordination deformation along the pile-soil interface was considered as well. Then, force and displacement boundary conditions were introduced to deduce the analytical solutions for the inner forces and deformation of the pile shaft under ideal elastic-plastic bearing stages of subsoil. Based on the obtained solutions, various combined values and loading sequencesofandat the pile top were adopted to determine the bearing capacity of the pile shaft, from which failure envelops were plotted correspondingly. Further numerical analyses were carried out by ABAQUS to find out the failure mechanism and the key factors that affect the bearing capacity of−combined loaded piles. The results show that the bearing capacity of pile shaft increases with the increase of aspect ratio, while decreases with the increase of the ratio of the constant coefficient of the subsoil shear modulus distribution function to that in the stiffness ratio (λ) of pile shaft to subsoil. Increasing the torsion (or the vertical force) at the pile top will decrease the vertical (or torsional) bearing capacity of a final zero value.

pile foundations;−combined loads; non-homogeneous subsoil; load transfer functions; numerical analysis

10.11817/j.issn.1672−7207.2018.10.023

TU473.1

A

1672−7207(2018)10−2553−08

2017−10−12；

2017−12−21

国家自然科学基金资助项目(51578231，51378197)(Projects(51578231, 51378197) supported by the National Natural Science Foundation of China)

邹新军，博士，副教授，从事地基基础与支挡结构研究；E-mail :xjzouhd@hnu.edu.cn