温升荷载下带裂工作的纵连板轨道温度力研究
2018-11-13刘笑凯李威肖杰灵刘学毅全毅
刘笑凯,李威,肖杰灵,刘学毅,全毅
温升荷载下带裂工作的纵连板轨道温度力研究
刘笑凯1, 2,李威1, 2,肖杰灵1, 2,刘学毅1, 2,全毅1, 2
(1. 西南交通大学 高速铁路线路工程教育部重点实验室,四川 成都,610031;2. 西南交通大学 土木工程学院,四川 成都,610031)
针对带裂工作的纵连板式轨道,研究温升荷载作用下板内温度力的分布规律及其影响因素。根据结构温度力计算理论,推导带裂工作的纵连板式无砟轨道在温升荷载下的温度压力计算公式,并结合试验,分析不同板底约束、配筋率和轨道板混凝土弹性模量条件下裂纹对轨道纵向温度压力的影响。研究结果表明:裂纹对纵连式无砟轨道的纵向温度压力影响较大,在计算时应当考虑裂纹对纵向温度压力的影响;摩阻系数对轨道板的纵向力影响较小,计算时可不考虑;板底黏结力对轨道板纵向温度压力影响较大,板底黏结力的增加会大幅度增加裂纹闭合所需的升温值并减少因裂纹而损失的温度;配筋率越高,轨道板的纵向温度压力越高,轨道板释放的温度压力越小,但配筋率对轨道板的纵向温度压力的影响较小。板底黏结状态和轨道板配筋率应当作为计算轨道板温度压力的重要参数。
纵连式无砟轨道;裂纹;温度压力;温升荷载
以CRTSⅡ型板式无砟轨道为代表的纵连式轨道结构是一类具有连续、均匀弹性支承的无砟轨道,结构整体性强、均匀性好,在我国应用较为广泛;但因结构变形受到限制,温度荷载和混凝土收缩均在轨道板(道床板)内产生巨大的纵向作用力[1−2]。在纵向力的作用下,轨道结构出现了诸如宽窄接缝伤损和轨道板上拱等病害,并产生大量的横向裂纹,严重影响结构的安全和使用寿命,威胁行车安全[3]。研究发现,无砟轨道裂缝形式主要有4种[3]:1)轨道板非预裂缝裂缝;2) 轨道板宽接缝后浇混凝土的裂纹;3) 沥青砂浆与轨道板离缝;4) 沥青砂浆斜裂纹。其中轨道板非预裂纹裂纹和轨道板宽接缝后浇混凝土的裂纹,属于常见的轨道板横向裂纹。横向裂纹的产生与低温、结构病害、新旧混凝土界面状态等有关[4−10]。其中,轨道板的横向裂纹对纵向温度力影响最大;受温升荷载时,将释放部分纵向温度压力,板内温度力场不再是均匀分布。朱胜阳等[11]已对温度荷载作用下的轨道结构的损伤进行了研究,但其并未考虑裂纹对温度压力的影响;王平等[12−14]研究了裂纹对轨道结构的受力的影响,但并未给出明确的温度压力的计算方法;李学平等[15]研究了带裂纹的梁的振动特性,但没有考虑温度力的影响。因此,深入研究带横向裂纹的纵连式无砟轨道(简称“带裂工作的纵连板轨道”)在温升荷载作用下的温度力计算方法和分布规律,有助于纵连式无砟轨道的安全应用和科学养护,具有重要的现实意义。
1 带裂工作的纵连板轨道温度压力的计算
考虑轨道板板底阻力、配筋率以及混凝土强度下裂纹对温升荷载作用的影响[16−17],假定如下:
1) 假设轨道板存在横向通裂,裂纹平均分布,板内应力在断面内均匀分布;
2) 假定钢筋与混凝土之间的黏结强度为固定值,并等于其黏结强度。
无裂纹时,轨道板所受纵向温度压力可按下式计算为
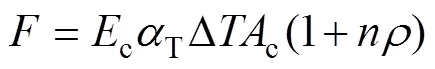
式中:n=Es/Ec,Es和Ec分别为钢筋和混凝土的弹性模量;αT为轨道板混凝土的线膨胀系数;Ac为轨道板截面混凝土面积;ρ为轨道板断面配筋率。
有裂纹时,裂纹附近的轨道板结构受力如图1 所示。其中:cr为裂纹间距;s为钢筋锚固区长度;x为板底阻力达到最大时的作用长度;l为裂纹宽度;c和s分别为两裂纹间混凝土和钢筋的最大应力;c1为板底阻力作用区端部混凝土的应力;sl为钢筋锚固区端部钢筋的应力;为钢筋与混凝土之间单位长度上的黏结力;2为板底作用力,若板底承受的摩阻力,2=c,为板底摩阻系数,为轨道混凝土重度。若板底承受黏结力,可表述为2=v,v取混凝土的抗拉强度t,为轨道宽度。
随着轨道板的温度的升高,根据裂纹的闭合状态的不同,可将此过程分为3个阶段:1) 第一阶段,轨道板未产生纵向伸缩,板底阻力未完全参与工作; 2) 第二阶段,板底阻力全部参与工作,但裂纹尚未完全闭合;3) 第三阶段,裂纹完全闭合。各阶段裂纹的收缩量的计算如下。
1.1 第一阶段
在第一阶段,s2xcTΔc(1+),x=[cTΔc(1+)−s]。轨道板混凝土应力分布和钢筋应力分布如图2所示。
钢筋锚固长度计算公式为y/t。当0<l<y/t时,s=l;当y/t<l<cr/2时,s=y/t。钢筋与混凝土之间的单位长度上的黏结阻力为=tc/()。式中:y为钢筋抗拉强度;t为混凝土抗拉强度;为钢筋直径;为钢筋形状系数;光圆钢筋取0.16,带肋钢筋取0.14。
轨道板压力最大值出现在两裂纹中间的截面为

在轨道板开裂处轴向力最小,仅钢筋承受为
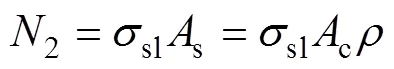
此时,1−2=2x。代入得
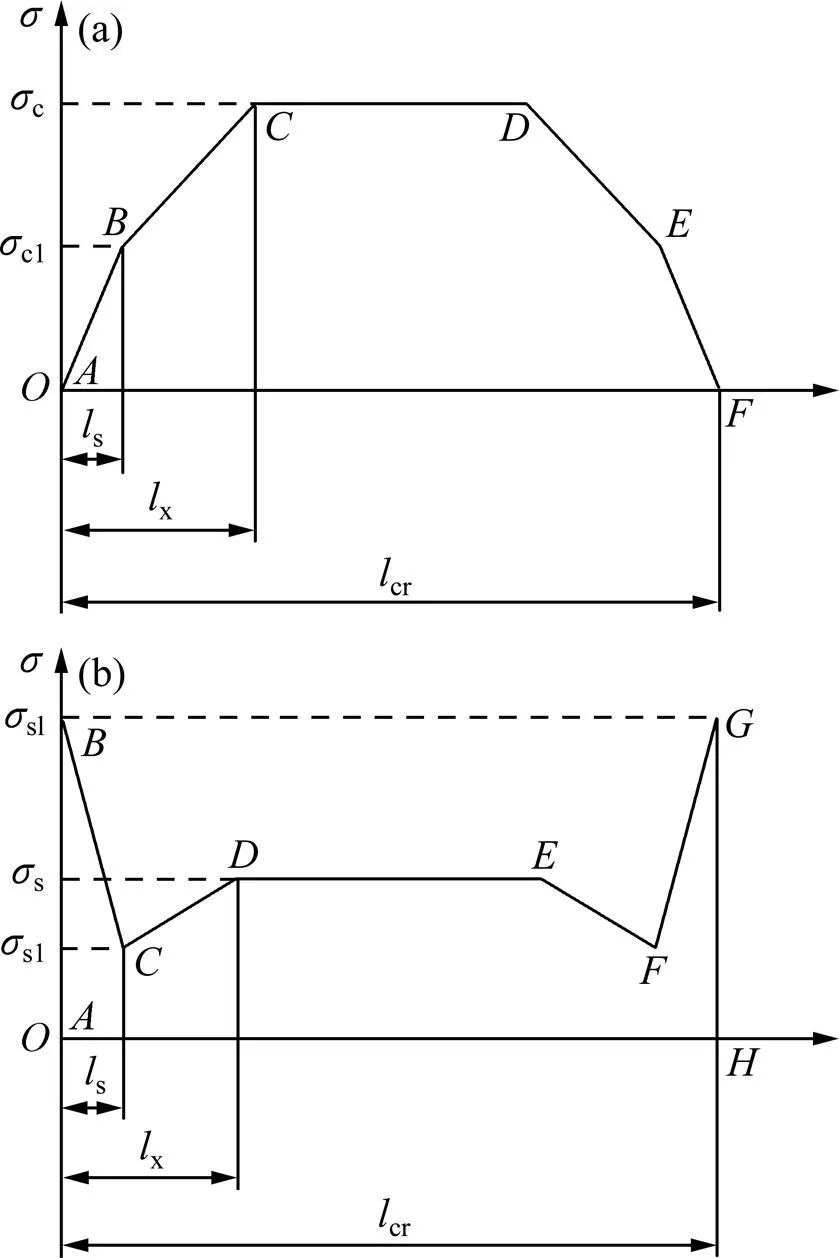
(a) 轨道板横向开裂;(b) 轨道板断面通裂

同理得

此时,
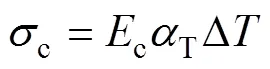
以两裂纹中间截面的轴向力代表轨道内部的轴向力:
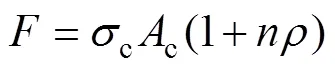
此时,裂纹缩小量为

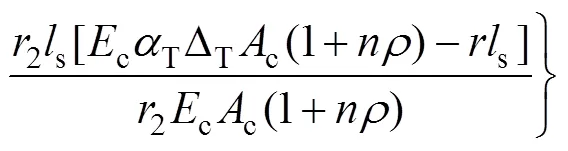
1.2 第二阶段
第二阶段轨道板混凝土应力分布和钢筋应力分布如图3所示。
在第二阶段,板底阻力全部参与工作,x=cr/2。此时,1−2=2cr/2。代入得

(a) 混凝土温度应力分布;(b) 板内钢筋纵向应力分布
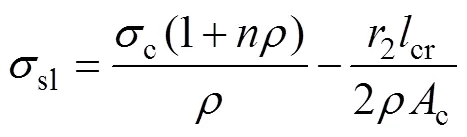
同理得
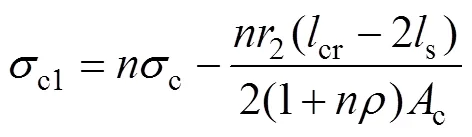
在升温过程中,钢筋的总长度保持不变,即钢筋的受压缩短量与升温伸长量相等,在连续轨道升温情况下,混凝土与钢筋的线膨胀系数T可视为相等,有

由式(8)~(10)可求得

裂纹总收缩量为
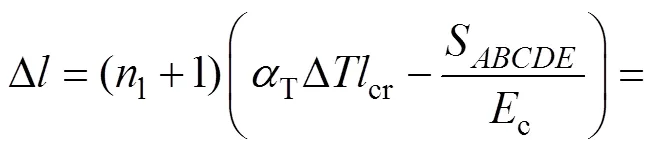
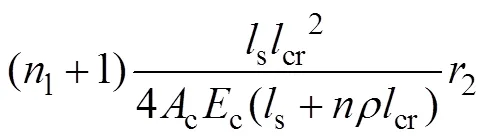
1.3 第三阶段
在第三阶段,裂纹总收缩宽度达到原裂纹宽度后,轨道纵向力增量与升温增量将呈线性关系。此时,两裂纹中间混凝土应力为
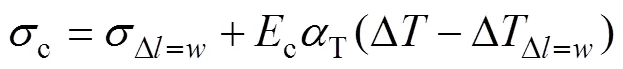
综上,可以求得轨道板各阶段的温度应力,以两裂纹中间截面的轴向力代表轨道内部的轴向力:
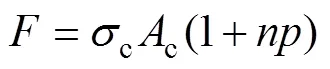
2 带裂工作的纵连板轨道温度压力的计算
为研究轨道板横裂对板内纵向温度压力的影响,建立长6.5 m、板底全部脱空的纵连板式轨道缩尺模型,模型比例1:5。通过人工加温模拟结构的整体升温,试验研究温升荷载对纵连结构的响应。模型利用混凝土自身收缩和温度荷载作用产生8条横向贯通的自然裂纹。通过板端加力的方式模拟整体升温,并通过与力学计算结果对比,分析带裂工作的无砟轨道对其内纵向温度压力分布的影响。试验模型示意图如图4所示,模型上典型裂纹如图5所示。
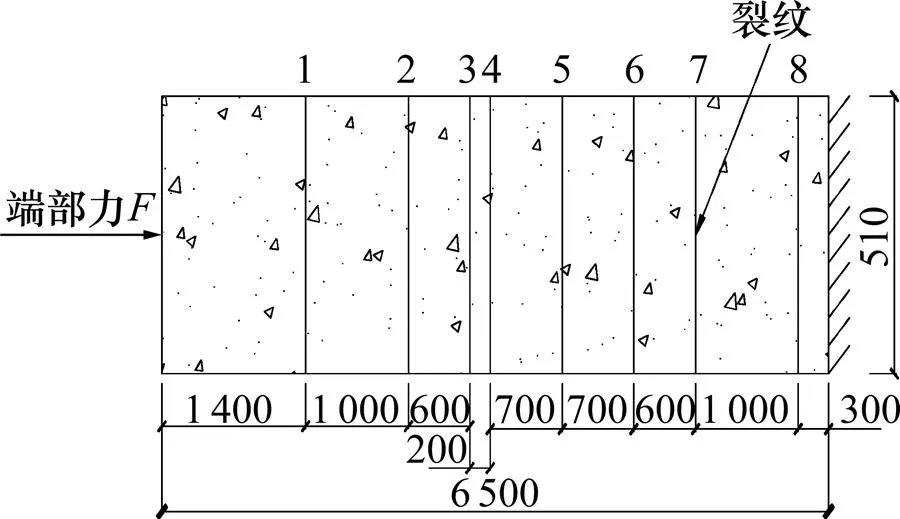
单位:mm
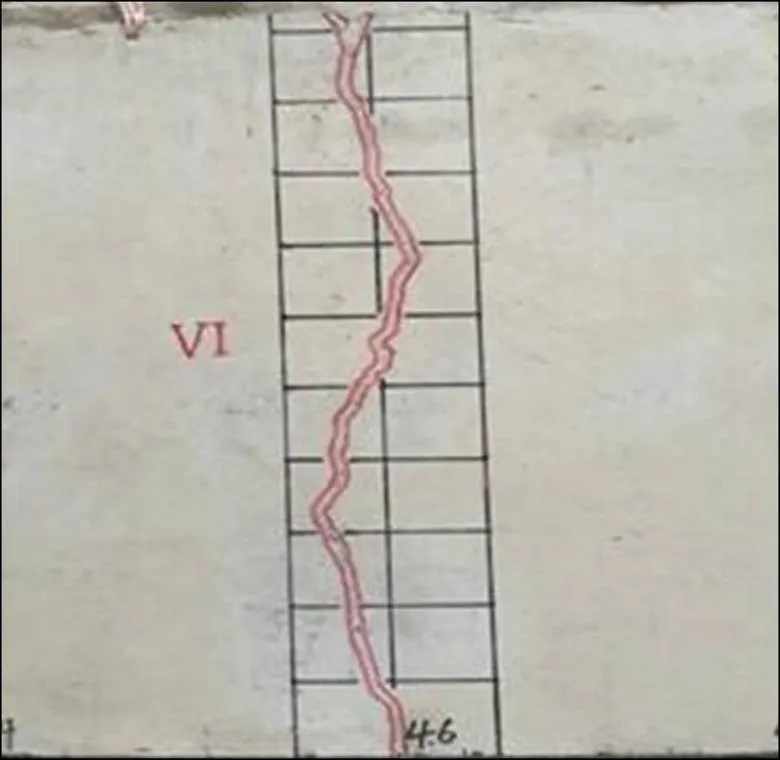
图5 轨道板裂纹
模型中轨道板和板下调整层采用C40混凝土,板内纵向钢筋选配5根φ6的HRB335钢筋,配筋率为=0.693%。轨道板与调整层之间摩阻系数测定为0.6。轨道板表面的8条横裂呈不等间距分布,试验前测量每条裂纹的宽度,裂纹总宽度为1.92 mm,各裂纹宽度如表1所示。

表1 模型裂纹宽度
试验通过在模型一端施加纵向力,并用百分表测量每一条裂纹在不同端部压力下的宽度,纵向力分别为7.5,15.0,22.5,30.0,37.5,45.0,52.5和 60.0 kN。通过试验得到模型所受纵向力和裂纹收缩量之间的关系如图6所示。由图6可见:大部分裂纹是随着端部力的增加同步闭合的,摩擦力对裂纹的闭合次序影响很小,这表明通过端部加力的方式模拟轨道板整体升温是合理的。在纵向力为60 kN时,所有裂纹的收缩量达到原裂纹宽度,裂纹处于闭合状态。
为验证计算公式的正确性,将试验和计算结果进行对比,如图7所示。由图7可知:两者得到的曲线较为吻合。当纵向力达到60.55 kN时,裂纹完全闭合,两结果相差仅为0.83%左右,验证了公式计算的可 靠性。
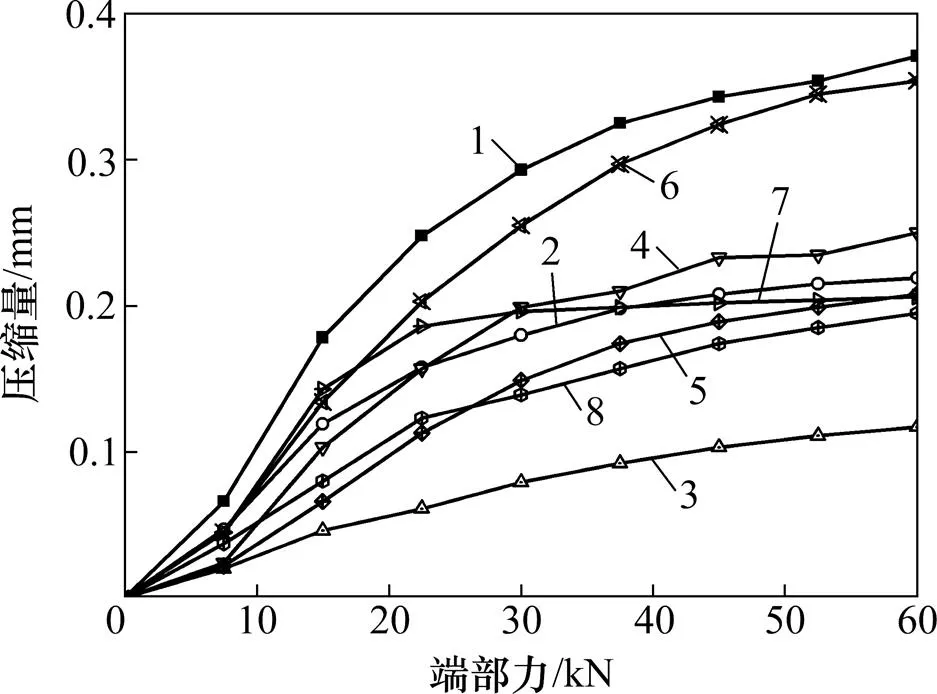
1—1号裂纹;2—2号裂纹;3—3号裂纹;4—4号裂纹;5—5号裂纹;6—6号裂纹; 7—7号裂纹;8—8号裂纹。

1—试验;2—理论计算。
3 影响因素分析
3.1 板底约束的影响
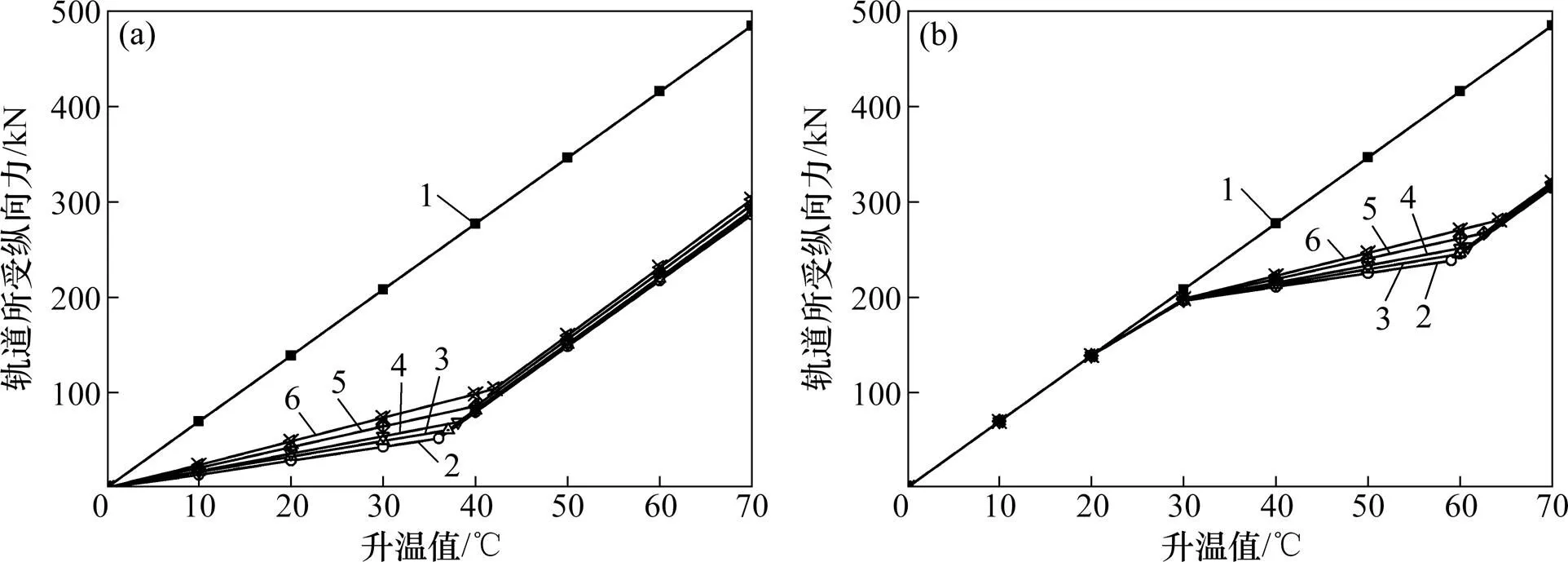
下部结构对轨道的纵向约束与层间状态有关,层间脱空时主要表现为摩阻力,其与摩阻系数和轨道自重有关,层间黏结时主要表现为材料间的相互黏结力。考虑到摩阻系数受界面状态影响大,其值离散,分别取为0.3,0.6,0.8,1.0和1.5进行研究。当轨道板底与调整层处于黏结状态时,为研究黏结力对温度压力分布的影响,分别取黏结应力为0.50,1.00,1.50和1.71 MPa进行计算。计算结果如图8所示。
由图8可知:当轨道板底全部脱空时,不同摩阻系数对轨道所受纵向力和裂纹的闭合影响极小。当整体升温约37 ℃时裂纹完全闭合,轨道所受纵向力为60.55 kN,与无裂纹时相比释放了195.93 kN的温度压力。当轨道板底受黏结力作用时,黏结力越大,裂纹完全闭合所需的升温值越高,相同的升温值下轨道所受纵向力越小,裂纹闭合后释放掉的温度压力也越大。当黏结应力为0.5 MPa,升温48.4 ℃时裂纹完全闭合,此时轨道所受纵向力为152.5 kN,释放了182.77 kN的温度压力。
3.2 配筋率的影响
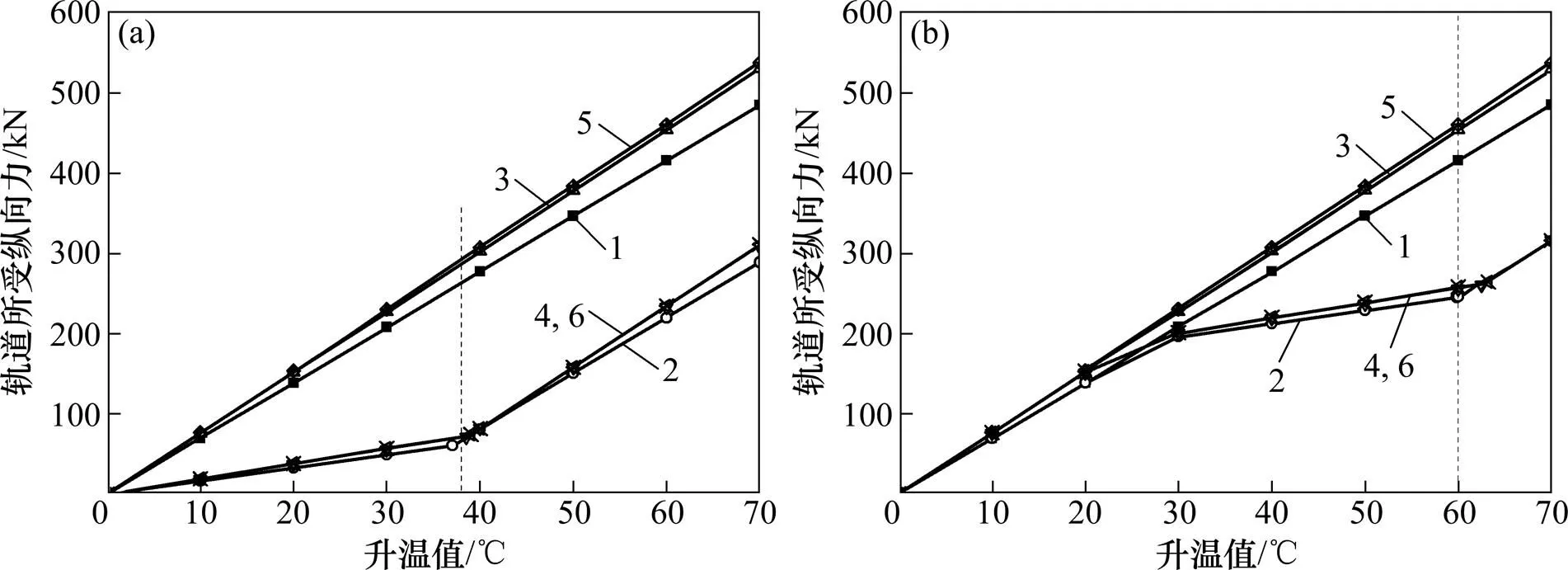
由式(8)和式(9)可知:当板底所受阻力2不变时,裂纹闭合所需的升温值和轨道板所受纵向力主要受配筋率以及轨道混凝土弹性模量的影响。分别考虑配筋率为0.600%,0.693%,0.800%,1.000%和1.200%,计算轨道板在不同温升荷载下的纵向力,设摩阻系数为0.6(试验测试值),板底未完全脱黏,黏结应力为1.000 MPa,计算结果如图9所示。
(a) 摩阻系数的影响;(b) 黏结应力的影响
3.3 混凝土弹性模量的影响
参考规范[18],分别取标号为C30,C40,C55和C60的混凝土作为轨道板材料,取其弹性模量分别为30.0,32.5,35.5和36.0 GPa,设摩阻系数为0.6,板底黏结应力为1 MPa,计算裂纹对轨道纵向温度压力的影响,结果如图10所示。
由图10可知:在不同板底约束下,不同混凝土弹性模量下带裂纹的轨道板的纵向力随升温的变化曲线较为接近,当混凝土弹性模量从32.5 GPa增加到 36.0 GPa时,相同温度下的轨道板纵向力和裂纹完全闭合所需的升温值都有所增加,但是增加幅度不大。说明当存在裂纹时,轨道混凝土弹性模量对轨道所受纵向力影响较小。
(a) 板底受摩阻力;(b) 板底受黏结力
(a) 板底受摩阻力;(b) 板底受黏结力
4 结论
1) 横向裂纹对纵连式无砟轨道的纵向温度压力影响较大,温度力沿纵向分布不均,在分析轨道结构纵向温度力时不应忽略其影响。
2) 板下摩阻系数对轨道板的纵向力影响极小,但板底黏结力的增加会大幅延缓裂纹的闭合,减少温度压力的损失。
3) 配筋率越高轨道板的纵向温度压力越高,轨道板释放的温度压力越小。
4) 轨道板混凝土弹性模量越高轨道板的纵向温度压力越高,轨道板释放的温度压力越小。
[1] 何华武. 无砟轨道技术[M]. 北京: 中国铁道出版社, 2006: 74−86. HE Huawu. Ballastless track technology[M]. Beijing: China Railway Press, 2006: 74−86.
[2] 徐庆元, 张旭久. 高速铁路博格纵连板桥上无砟轨道纵向力学特性[J]. 中南大学学报(自然科学版), 2009, 40(2): 526−532. XU Qingyuan, ZHANG Xujiu. Longitudinal forces characteristic of Bogl longitudinal connected ballastless track on high-speed railway bridge[J]. Journal of Central South University(Science and Technology), 2009, 40(2): 526−532.
[3] 刘亚男. 复杂温度下Ⅱ型板式无砟轨道宽窄接缝病害影响及维修措施[D]. 北京: 北京交通大学土木工程学院, 2016: 2−18. LIU Yanan. Research on the wide-narrow juncture diseases influence and mainnance of CRTS II slab ballastless track under complex temperature[D]. Beijing: Beijing Jiaotong University. College of Civil Engineering, 2016: 2−18.
[4] 杨金成. Ⅱ型板无砟轨道结构裂缝产生机理及修补方案研究[J]. 石家庄铁道大学学报(自然科学版), 2012, 25(2): 54−58, 72.YANG Jincheng. Research on generating mechanism and repairing scheme of structural cracks of CRTSⅡin high speed railway[J].Journal of Shijiazhuang Tiedao University (Natural Science), 2012, 25(2): 54−58, 72.
[5] MEREDITH P G, ATKINSON B K. Fracture toughness and subcritical crack growth during high-temperature tensile deformation of Westerly granite and Black gabbro[J]. Physics of the Earth & Planetary Interiors, 1985, 39(1): 33−51.
[6] HILLERBORG A, MODÉER M, PETERSSON P E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements[J]. Cement & Concrete Research, 2008, 6(6): 773−781.
[7] AKKAYA Y, OUYANG C, SHAH S P. Effect of supplementary cementitious materials on shrinkage and crack development in concrete[J]. Cement & Concrete Composites, 2007, 29(2): 117−123.
[8] MATALLAH M, BORDERIE C L, MAUREL O. A practical method to estimate crack openings in concrete structures[J]. International Journal for Numerical & Analytical Methods in Geomechanics, 2010, 34(15): 1615−1633.
[9] TIBERTI G, MINELLI F, PLIZZARI G A, et al. Influence of concrete strength on crack development in SFRC members[J]. Cement & Concrete Composites, 2014, 45(1): 176−185.
[10] 张莹涛. 基于扩展有限元法的双块式无砟轨道裂纹扩展特性研究[D]. 石家庄: 石家庄铁道大学土木工程学院, 2015: 3−12. ZHANG Yingtao. The extending features of the crack existed in continuous double-block ballastless track based on XFEM[D]. Shijiazhuang: Shijiazhuang Tiedao University. College of Civil Engineering, 2015: 3−12.
[11] 朱胜阳,蔡成标. 温度和列车动荷载作用下双块式无砟轨道道床板损伤特性研究[J]. 中国铁道科学, 2012, 33(1): 6−12. ZHU Shenyan, CAI Chengbiao. Study on damage characteristics of double-block ballastless track bed plate under temperature and train dynamic load[J]. China Railway Science, 2012, 33(1): 6−12.
[12] 王平, 徐浩, 陈嵘, 等. 路基上CRTS Ⅱ型板式轨道裂纹影响分析[J]. 西南交通大学学报, 2012, 47(6): 929−934. WANG Ping, XU Hao, CHEN Rong, et al. Effects analysis of cracking of CRTS Ⅱ slab track on subgrade[J]. Journal of Southwest Jiaotong University, 2012, 47(6): 929−934.
[13] 吴欢. 含裂纹CRTSI型双块式无砟轨道受力分析[D]. 成都: 西南交通大学土木工程学院, 2011: 44−45. WU Huan. The stress analysis of the CRTS I bi-block slab track with cracks[D]. Chengdu: Southwest Jiaotong University. College of Civil Engineering, 2011: 44−45.
[14] 张勇. 路基上双块式无砟轨道空间力学及裂纹特性研究[D]. 长沙: 中南大学土木工程学院, 2011: 59−60. ZHANG Yong. Study on spatial mechanics and crack characteristics of double-block ballastless track on subgrade[D]. Changsha: Central South University. College of Civil Engineering, 2011: 59−60.
[15] 李学平, 余志武. 含多处裂纹梁的振动分析[J]. 应用力学学报, 2007, 24(1): 66−68. LI Xueping YU Zhiwu. Vibration analysis to multipl cracked beam[J]. Chinese Journal of Applied Mechanics, 2007, 24(1): 66−68.
[16] 刘学毅, 赵坪锐, 杨荣山, 等. 客运专线无砟轨道设计理论与方法[M]. 成都: 西南交通大学出版社, 2010: 161−200. LIU Xueyi, ZHAO Pingrui, YANG Rongshan, et al. Design theory and method of ballastless track for passenger dedicated line[M]. Chengdu: Southwest Jiaotong University Press, 2010: 161−200.
[17] 戴公连, 刘瑶, 刘文硕. 大跨度连续梁桥与梁拱组合桥梁轨相互作用比较[J]. 中南大学学报(自然科学版), 2017, 48(1): 233−238. DAI Gonglian, LIU Yao, LIU Wenshuo. Comparison of track-bridge interaction between long-span continuous girder bridge and continuous arch bridge[J]. Journal of Central South University(Science and Technology), 2017, 48(1): 233−238.
[18] GB 50010—2010, 混凝土结构设计规范[S]. GB 50010—2010,Code for design of concrete structures[S].
(编辑 杨幼平)
Study of longitudinal temperature pressure of longitudinal ballastless track with cracks
LIU Xiaokai1, 2, LI Wei1, 2, XIAO Jieling1, 2, LIU Xueyi1, 2, QUAN Yi1, 2
(1. MOE Key Laboratory of High-speed Railway Engineering, Southwest Jiaotong University, Chengdu 610031, China; 2. School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China)
With consideration of the longitudinal temperature pressure characteristics of longitudinal ballastless track with crack, formula of longitudinal temperature pressure of longitudinal ballastless track with crack was deduced. Through the experiment, effects of different slab bottom constraints, reinforcement ratio and elastic modulus of slab on the longitudinal temperature pressure of track were analyzed. The results show that the influence of the crack on the longitudinal temperature pressure of the longitudinal ballastless track is large, and the influence of the crack on the longitudinal temperature pressure should be taken into account in the calculation. The friction coefficient has little effect on the longitudinal force of slab, and it is not considered in calculating. The bond force has a large effect on the longitudinal temperature pressure of slab. The increase in the bond force at the bottom of slab leads to a big rise in the temperature which is required for the crack closure and reduces the temperature pressure loss caused by cracking. To a small extent, the higher the reinforcement ratio is, the higher the longitudinal temperature of the track plate is and the smaller the temperature pressure released by the track plate becomes. State and of slab bottom and reinforcement ratio of slab should be used as important parameters for calculating the temperature pressure of slab.
longitudinal ballastless track; cracks; temperature pressure; load of temperature rise
10.11817/j.issn.1672−7207.2018.10.020
U213.2+44
A
1672−7207(2018)10−2526−07
2017−10−22;
2017−12−24
国家自然科学基金资助项目(U1434208,U1534203,51678506);四川省科技计划项目(2016GZ0333)(Projects(U1434208, U1534203, 51678506) supported by the National Natural Science Foundation Program of China; Project(2016GZ0333) supported by Science and Technology Program of Sichuan Province)
肖杰灵,博士,讲师,从事高速、重载及城市轨道交通轨道结构和轨道动力学研究;E-mail:xjling@swjtu.cn
