粒化单调的条件邻域熵及其相关属性约简
2018-11-13周艳红张贤勇莫智文
周艳红 张贤勇 莫智文
1(四川师范大学数学与软件科学学院 成都 610068) 2(中国民用航空飞行学院计算机学院 四川广汉 618307) 3 (四川师范大学智能信息与量子信息研究所 成都 610068) (zhouyanhong515@163.com)
粗糙集理论是一种有效处理不确定性问题的新型数学工具[1],已经广泛应用于机器学习与模式识别等领域[2].属性约简是粗糙集理论进行知识发现与优化处理的基础,具有重要的应用意义,近年来呈现诸多研究成果.文献[3]提出基于正域的启发式属性约简算法;文献[4]研究4种不同熵的属性重要度秩保持性质,并提出增量式属性约简算法;文献[5]基于最大依赖性、最大相关性与最小冗余性原则提出基于互信息的启发式算法;文献[6-7]利用双量化思想探讨层次约简,提出3层粒结构(微观底层、中观中层、宏观高层)的构建方法;文献[8]提出一种基于相对决策熵的属性约简算法.
经典粗糙集主要以等价关系与等价类为基础,能够有效处理离散型数据,但在处理连续型数据方面具有局限性.对此,邻域粗糙集拓展经典粗糙集并适用于数值型及混合型数据分析.文献[9]提出邻域关系,文献[10]提出邻域互信息,文献[11]提出邻域类,文献[12-19]则对邻域信息系统进行了深入研究.其中,文献[12]在邻域信息系统中提出邻域熵,并进行系列研究;文献[13]将Shannon 熵与邻域熵结合提出邻域互信息并做属性约简;文献[15]利用邻域互信息[10]发展属性约简;文献[16]提出基于3支决策的邻域熵与条件邻域熵并做属性约简;文献[17]构造基于邻域粗糙集的多标记分类任务的特征选择算法;文献[18]开发基于邻域粒化与粗糙逼近的数值属性约简算法;文献[19]利用邻域粗糙集中的熵度量来研究基因选择.
综上可见,在邻域粗糙集中,基于信息度量的属性约简具有研究价值与应用意义.事实上,邻域熵、条件邻域熵与邻域互信息已经系统地存在[10].但是,其中的条件邻域熵具有粒化非单调性,不能建立约简的核与启发式算法;此外,鉴于对数函数定义域,该条件邻域熵没有考虑“0概率信息项”,从而带来不自然的熵值突变;进而,这些具体情况阻碍了相关属性约简的后续发展.本文主要针对经典条件邻域熵[10]及其缺陷,进行改进并提出具有粒化单调性的条件邻域熵,进而依托信息增量的可控性来研究相关的属性约简.
1 邻域信息系统及条件邻域熵
1.1 邻域信息系统的基本知识
邻域信息系统是邻域粗糙集的基本背景,本节复习其基本知识.
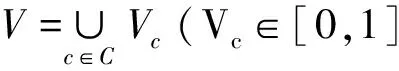
本文主要涉及邻域决策系统DS.针对DS与IS,设A,B⊆C={c1,c2,…,cn}.
定义2[11]. 距离函数.在IS中,设x,y∈U,则C的距离函数为
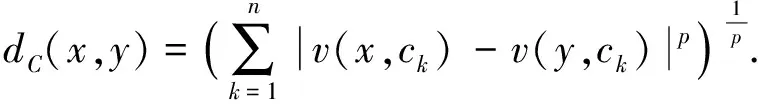
(1)
若p=1,dC(x,y)为Manhattan距离;若p=2,dC(x,y)为Euclidean距离;若p=∞,dC(x,y)为Chebychev距离.
距离函数在邻域粗糙集中起着核心作用,这里dC自然诱导dA,dB.本文主要采用Chebychev距离(详细计算参见文献[20]).
定义3[11]. 邻域和邻域关系.在IS中,x∈U在B上的δ邻域为
B决定的邻域关系为
NRδ(B)={(x,y)∈U×U|dB(x,y)≤δ}.
UNRδ(B)记U上基于B的覆盖,即由邻域关系决定的邻域集.
性质1[12]. 邻域是邻域粗糙集中的基本粒,具有2项单调性质:
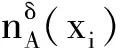
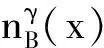
基于邻域,文献[10]研究了IS中的信息度量,包括邻域熵、条件邻域熵与邻域互信息等,相关定义与性质如下.
定义4[10]. 邻域熵.在IS中,B的邻域熵为
(2)
定义5[10]. 条件邻域熵、联合邻域熵、邻域互信息.在IS中,A关于B的条件邻域熵为
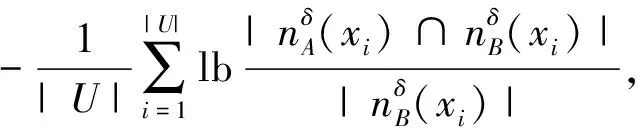
(3)
A与B的联合邻域熵为
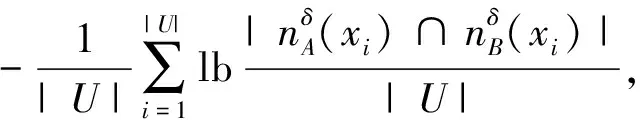
(4)
A与B的邻域互信息为

(5)
定理1[10].
1)NMIδ(A;B)=NMIδ(B;A);
2)NMIδ(A;B)=NHδ(A)+NHδ(B)-NHδ(A∪B).
文献[10]还考虑条件B的邻域结构与决策D的分类结构,将IS中的条件邻域熵落实到了DS中.为了更好地分析信息本质与层次机制,定义6给出一种范化形式.
定义6. 条件邻域熵.在DS中,D关于B的条件邻域熵为
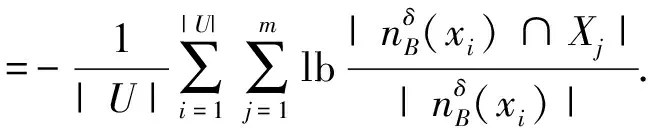
(6)
1.2 条件邻域熵的粒化非单调性
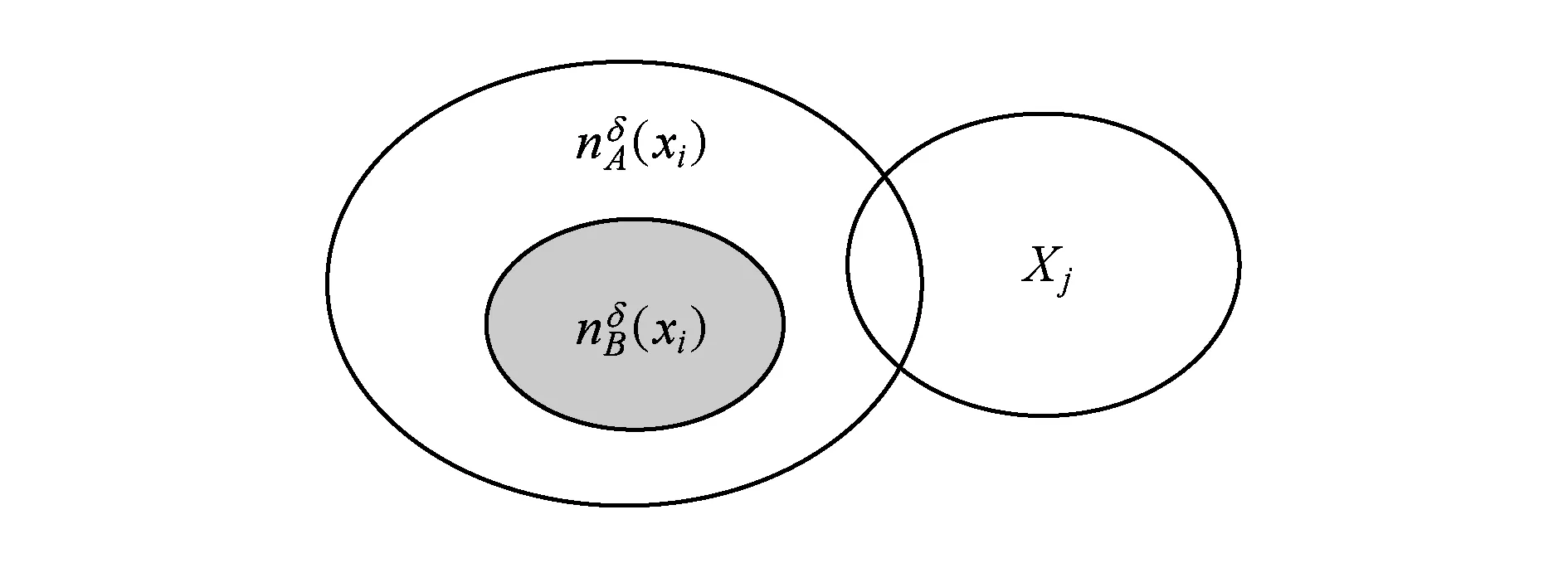
针对DS中的条件邻域熵(式(6)),下面采用3层粒化技术[6]进行“高层→中层→底层”层次分解(如图1左列),以待改进与比较.
式(6)位于宏观高层,能够转换为等价形式:
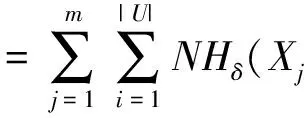
其中:
NHδ(Xj
如此,图1左列中的中层度量与底层度量具有相关的符号描述.
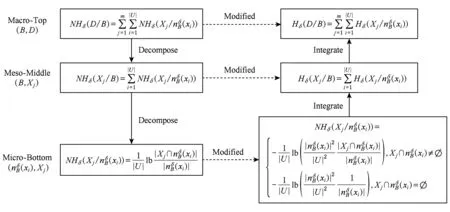
Fig. 1 Conditional neighborhood entropy and its improvement relationship based on three-layer granular structure图1 基于3层粒结构的条件邻域熵及其改进关系
由图1左列可知,高层NHδ(DB)由NHδ(Xj通过“ΣΣ” 表示;通过一次分解,中层NHδ(XjB)由NHδ(Xj通过“Σ” 表示;底层则由NHδ(Xj直接表示.可见,条件邻域熵具有3层分解形式,其粒化非单调性主要位于高层且具有如下层次诱因.
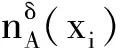
例1.DS=(U,C∪D,V,f,δ)如表1所示.其中,U={x1,x2,…,x7},C={c1,c2,…,c5},UD={X1,X2}={{x1,x2,x4,x5},{x3,x6,x7}},δ=0.4.

Table 1 Decision Table of Example 1表1 例1决策表
条件邻域熵(式(6))可以直接计算,其等价于实施“ΣΣ”集成图1左列中的底层度量.现选取粗化过程{c1,c2,c3,c4}→{c1,c2,c3}→{c1,c2},经计算3个条件邻域熵值可得:
NHδ(D{c1,c2})-NHδ(D{c1,c2,c3})=
9.6515×10-4>0;
NHδ(D{c1,c2,c3})-NHδ(D{c1,c2,c3,c4})=
-0.0157<0.
因此,在粗化{c1,c2,c3}→{c1,c2}中,
NHδ(D{c1,c2})>NHδ(D{c1,c2,c3}),
而在粗化{c1,c2,c3,c4}→{c1,c2,c3}中,
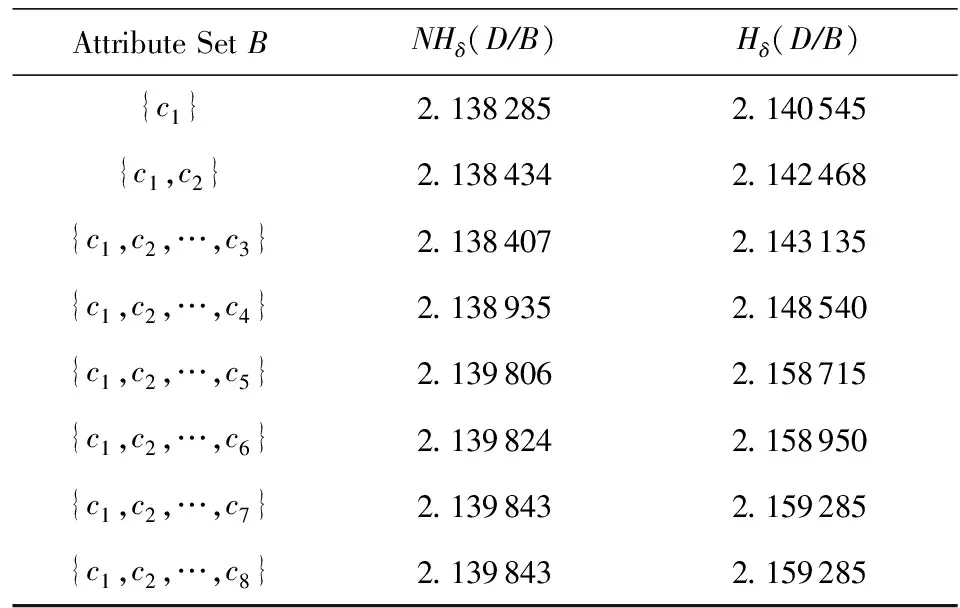
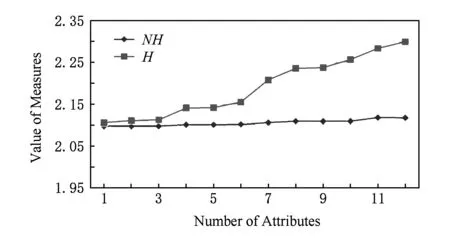
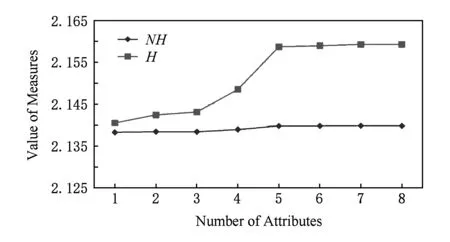
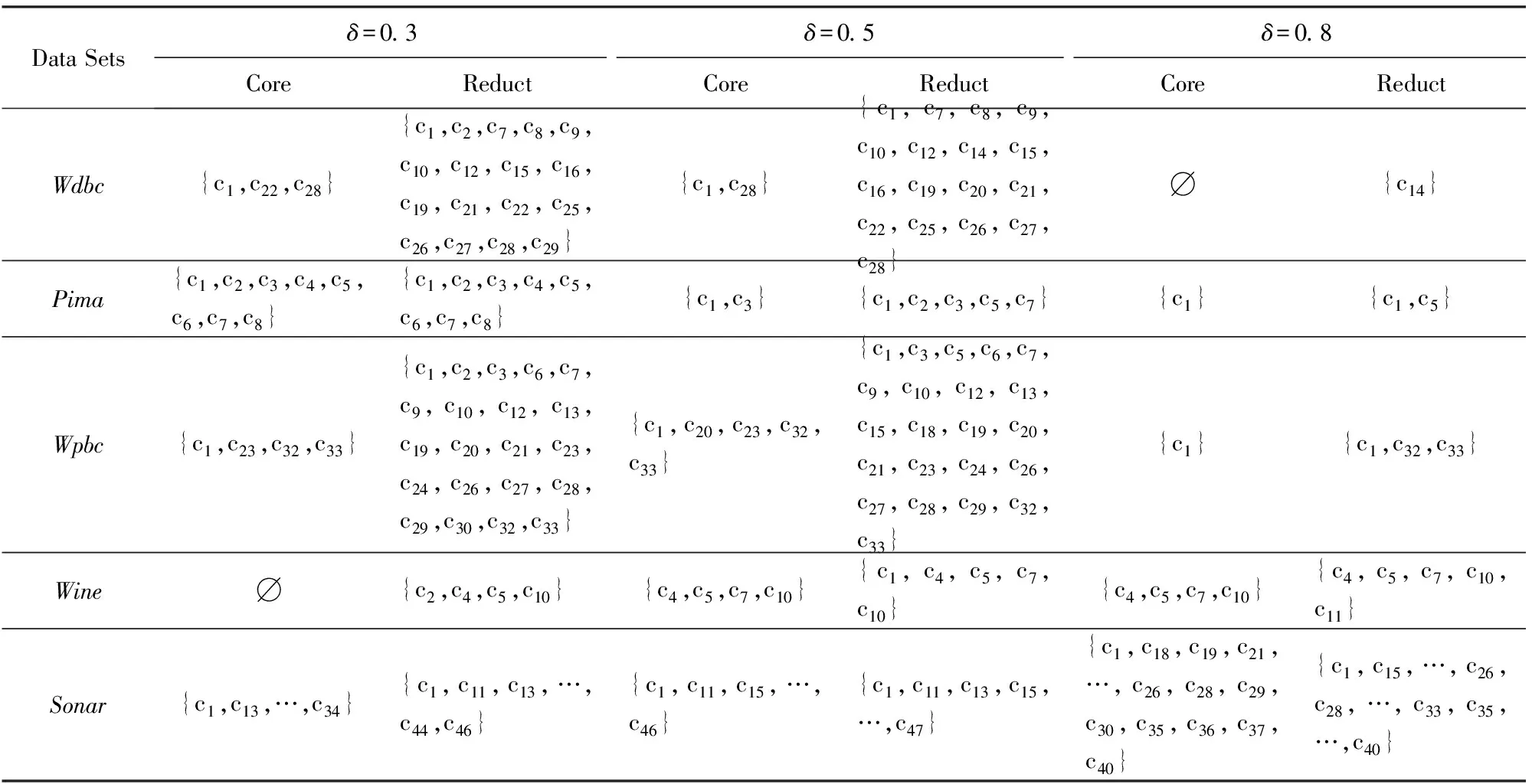
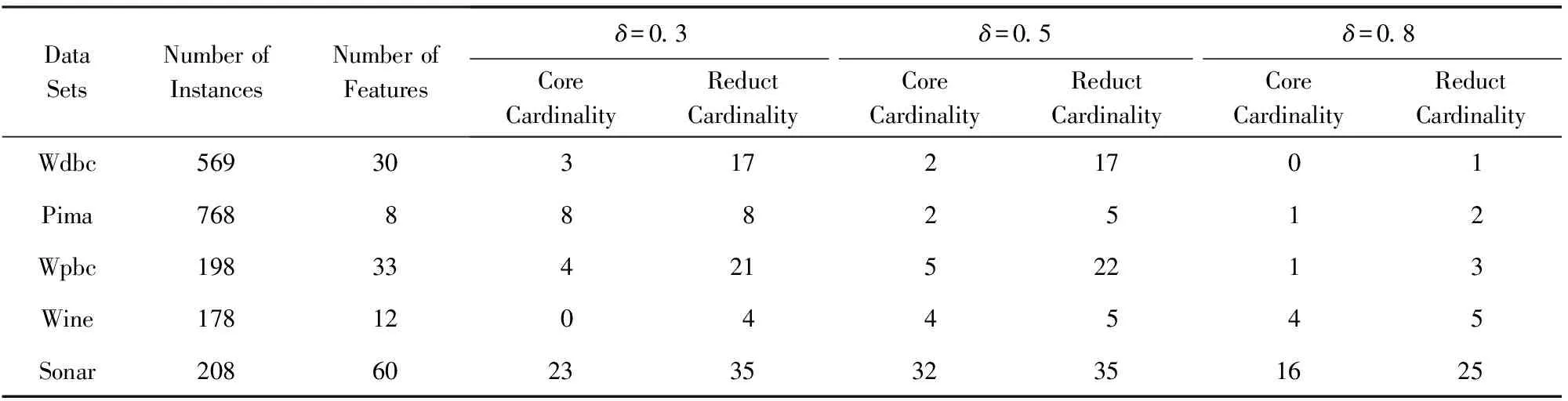
NHδ(D{c1,c2,c3}) 可见,条件邻域熵是粒化非单调的. Fig. 2 Qualitative change of intersection information in knowledge coarsening图2 知识粗化中的交信息质变 条件邻域熵(式(6))具有粒化非单调性的不足,相关的两大底层概率诱因是:1) 底层概率在粗化中的不确定性,2) 底层0概率没有被考虑.对此,本节采用3层粒结构[6]与自底向上粒计算策略,先改进条件邻域熵对应的底层度量,再集成构建具有粒化单调性的新型条件邻域熵. Hδ(Xj 即底层度量可以能够表示为不确定性信息 的线性集成(或者表示为其中一个的线性变换),故关联于集成的不确定性信息;基于Case1的设置,Case2利用“近似逼近”来获取信息度量变化的平稳性.因此,定义7所建度量主要具有数学优势. 性质2. 若A⊆B,则 Hδ(Xj 因此,粗化过程涉及3种粒相交情形,相关的分类与证明如下: 因此: 即Hδ(Xj 类似于情形1的证明过程,可得: Hδ(Xj 因此,Hδ(Xj 综上情形1~3,得证. 证毕. 性质2表明底层度量Hδ(Xj具有粒化单调性.特别地,证明中的情形2恰好可用图2来解释,故也说明定义7考虑了图2的“交信息质变”这一特殊情况. 性质3. 若0≤γ≤δ≤1,则 Hδ(Xj 定义7构建了新型底层度量,性质2与性质3分别体现了其相关的粒化单调性及参数单调性,因此其对条件邻域熵的底层分解度量具有改进性.下面,对该底层度量实施自然集成,获取中高层度量及其单调性,最终在高层改进条件邻域熵.特别地,基于底层度量的科学构造与信息集成,中高层度量也具有可解释性与相关不确定性语义. 定义8. 中层度量.在中层(B,Xj)定义度量 (7) 性质4. 若A⊆B,则 Hδ(XjB)≥Hδ(XjA). 性质5. 若0≤γ≤δ≤1,则 Hδ(XjB)≤Hγ(XjB). 定义8集成定义7底层度量构建了中层度量,其具有粒化单调性与参数单调性,这2条性质(即性质4与性质5)自然来源于底层的相应性质(即性质2与性质3).类似地,下面将中层的度量及其性质自然集成演化到高层. 定义9. 单调条件邻域熵.在高层(B,D)上定义单调条件邻域熵: (8) 性质6. 若A⊆B,则Hδ(DB)≥Hδ(DA). 性质7. 若0≤γ≤δ≤1,则 Hδ(DB)≤Hγ(DB). 定义9最终建立了具有粒化单调性(性质6)的条件邻域熵,其“自底向上”的集成演化标注于图1的右列.利用图1对条件邻域熵(定义6)与单调条件邻域熵(定义9)进行比较总结. 1) 图1左列体现了条件邻域熵的“高层→中层→底层”分解过程,即高层度量NHδ(DB)通过“Σ”分解到中层度量NHδ(XjB),再通过“Σ”分解到底层度量NHδ(Xj 2) 图1右列体现了单调条件邻域熵的“底层→中层→高层”集成过程,即底层度量Hδ(Xj通过“Σ”集成到中层度量Hδ(XjB),再通过“Σ”集成到高层度量Hδ(DB). 3) 定义6的条件邻域熵的“自顶向下分解”与定义9的单调条件邻域熵的“自底向上集成”具有相反性与对比性,但两者在3种粒度层次上具有横向改进性.具体地,在底层上Hδ(Xj改进NHδ(Xj在中层上Hδ(XjB)改进NHδ(XjB),在高层上Hδ(DB)改进NHδ(DB). 综上3点可见,现有工作已经涉及3项内容:1)对条件邻域熵进行3层分解,并揭示高层粒化非单调性及其底层诱因;2)自底向上构建新型条件邻域熵,从粒化机制上得到粒化单调性;3)从粒化单调性的角度,新型条件邻域熵在3个层次上都具有改进性. 目前,属性约简主要集中在粒化高层,其中的粒化单调度量是构建属性约简的重要基础.第2节通过底层的单调构造与0概率处理,在粒化高层建立了具有粒化单调性的条件邻域熵,其具有特定的不确定性语义.进而,本节采用新建单调条件邻域熵来自然研究属性约简,包括建立相关的定义、性质及算法等. 定理2. 2个条件等价: (N1)Hδ(DB)≠Hδ(D(B-{b})),∀b∈B; (N2)Hδ(DB′)≠Hδ(DB),∀B′⊂B. 证明. 1) 若∀B′⊂B,则∃b∈B-B′⊂B,使得B′⊆B-{b}⊂B.由粒化单调性(性质6)与N1,可知Hδ(DB′)≤Hδ(D(B-{b})) 2) ∀b∈B,设B′=B-{b}⊂B.由N2知Hδ(DB)≠Hδ(D(B-{b})),即N2⟹N1成立. 综上2点得证. 证毕. 定义10. 约简.引入新条件: (S)Hδ(DB)=Hδ(DC), 若子集B满足条件S与N1或条件S与N2,则称为C的一个相对D约简,所有相对约简组成的集合记为RedC(D). 基于单调条件邻域熵,定理2提供2条等价的独立必要性条件,即N1与N2.再加上联合充分性条件S,定义10自然定义相关的属性约简. 定义11. 核.若Hδ(D(C-{c}))≠Hδ(DC),则称c在C中是必要的,否则是不必要的.C中所有必要属性组成的集合称为核,记为CoreC(D),即: CoreC(D)={c∈C|Hδ(D(C-{c}))≠Hδ(DC)}. (9) Hδ(DB)=Hδ(DC),B⊆C-{c}⊂C, 由粒化单调性(性质6)可得: Hδ(D(C-{c}))=Hδ(DC). 由定义11知,c∉CoreC(D).因此 2) 若c∉CoreC(D),由定义11知: Hδ(D(C-{c}))=Hδ(DC). ∃B∈RedC(D),B⊆C-{c},使得: Hδ(D(C-{c}))=Hδ(DB). 由粒化单调性(性质6)知,Hδ(DB)=Hδ(DC),故B∈RedC(D).由B⊆C-{c}有c∉B,从而因此: 综上2点得证. 证毕. 类似于经典情形,定义11提供核计算公式,并可生成相关算法(如算法1);定理3表明核在所有约简中,因此可计算的核可以作为构建约简的基础.定义12首先利用单调条件邻域熵来建立属性重要度,进而设计基于核的启发式属性增加算法(如算法2). 定义12. 属性重要度.设c∈C-B,则属性c对条件属性集B相对于D的重要度为 Sig(c,B,D)=Hδ(DB∪{c})-Hδ(DB). (10) 其表征“B上增加属性c”增加过程中单调条件邻域熵的变化. 算法1. 求核算法. 输入:决策表DS=(U,C∪D,V,f,δ); 输出:CoreC(D). Step1. 计算Hδ(DC),设置CoreC(D)=∅; Step2. for ∀ck∈C(k=1,2,…,n) do Step3. 计算Hδ(D(C-{ck})); Step4. ifHδ(D(C-{ck}))≠Hδ(DC) then Step5.CoreC(D)=CoreC(D)∪{ck}; Step6. end if Step7. end for Step8. returnCoreC(D). 算法2. 基于核的属性增加启发式约简算法. 输入:决策表DS=(U,C∪D,V,f,δ); 输出:B∈RedC(D). Step1. 计算Hδ(DC); Step2. 由算法1,计算CoreC(D),取B= CoreC(D),计算Hδ(DB); Step3. whileHδ(DB)≠Hδ(DC) do Step4. ∀ck∈C-B,计算Sig(ck,B,D),取 c0=arg maxSig(ck,B,D); Step5. 令B=B∪{c0},计算Hδ(DB); Step6. end while Step7. returnB. 算法1通过逐个删除条件属性,并基于式(9)进行求核计算.算法2在算法1求核的基础上,采用属性重要度进行启发式搜索,快速增加条件属性来最终获取一个属性约简.具体地,Step3~6循环增加属性直至粒化单调条件邻域熵值达到最初C所在的最高水平,其中主要加入具有最大Sig值的属性(即Step4中的c0),以提升整个算法的收敛速度. 最后指出,算法1基本地计算核而算法2启发地搜索约简,两者都依托了改进条件邻域熵及其粒化单调性.对比地,传统条件邻域熵具有粒化非单调性,不能进行相关约简算法的有效构建与具体实现. 本节提供UCI(University of CaliforniaIrvine)数据实验,验证新建条件邻域熵的改进单调性与相关约简算法的有效性. 这里验证改进条件邻域熵的粒化单调性.为此,选取3类UCI数据集:Wdbc,Pima,Sonar[21].其中,Wdbc数据集包含569个对象、30个条件属性、1个决策属性;Pima数据集包含768个对象、8个条件属性、1个决策属性;Sonar数据集包含208个对象、60个条件属性、1个决策属性. 对每一类数据集,主要在确定邻域参数δ后选择一条属性扩充增链,从而计算条件邻域熵与改进条件邻域熵并分析它们的粒化单调性. 1) Wdbc数据集采用阈值δ=0.8,只关注前12个条件属性并构建一条具有自然序的属性增链 {c1}→{c1,c2}→{c1,c2,c3}→…→ 2) Pima数据集采用δ=0.95,并关注自然增链 {c1}→{c1,c2}→{c1,c2,c3}→…→ 3) Sonar数据集采用δ=0.4,只关注前15个条件属性及其构成的自然增链 {c1}→{c1,c2}→{c1,c2,c3}→…→ 在这些实验设计下,3种数据集的2种条件邻域熵值分别列入表2~4,它们对应地描绘于图3~5;其中,图3~5中横坐标及属性数目对应着属性增链,纵坐标熵值记录 NH=NHδ(D/B)与H=Hδ(D/B). Table 2 Values of Two Types of Conditional Neighborhood Entropy in Wdbc Dataset (δ=0.8) Table 3 Values of Two Types of Conditional Neighborhood Entropy in Pima Dataset (δ=0.95) Table 4 Values of Two Types of Conditional Neighborhood Entropy in Sonar Dataset (δ=0.4) Fig. 3 Changing curves of two types of conditional neighborhood entropy in Wdbc dataset (δ=0.8)图3 Wdbc数据集的2种条件邻域熵的变化曲线 (δ=0.8) Fig. 4 Changing curves of two types of conditional neighborhood entropy in Pima dataset (δ=0.95)图4 Pima数据集的2种条件邻域熵的变化曲线 (δ=0.95) Fig. 5 Changing curves of two types of conditional neighborhood entropy in Sonar dataset (δ=0.4)图5 Sonar数据集的2种条件邻域熵的变化曲线 (δ=0.4) 基于表2~4与图3~5结果,容易验证2种条件邻域熵的粒化单调性. 1) 在表2中,属性增链 {c1,c2,c3}→{c1,c2,c3,c4}→{c1,c2,c3,c4,c5} 涉及NHδ(DB)非单调变化 2.097 547→2.101 147→2.101 050 与Hδ(DB)单增变化 2.112 881→2.140 857→2.141 813; 而属性增链 {c1,c2,…,c10}→{c1,c2,…,c11}→{c1,c2,…,c12} 涉及NHδ(DB)非单调变化 2.109 760→2.118 238→2.117 672 与Hδ(DB)单增变化 2.256 689→2.283 208→2.298 845. 2) 在表3中,而属性增链 {c1}→{c1,c2}→{c1,c2,c3} 涉及NHδ(DB)非单调变化 2.138 285→2.138 434→2.138 407 与Hδ(DB)单增变化 2.140 545→2.142 468→2.143 135. 3) 在表4中,而属性增链 {c1,c2,…,c13}→{c1,c2,…,c14}→{c1,c2,…,c15} 涉及NHδ(DB)非单调变化 2.045 410→2.047 744→2.046 308 与Hδ(DB)单增变化 3.153 038→3.648 269→4.447 961. 由此可见,条件邻域熵不具备粒化单调性,而新建条件邻域熵具有改进性.事实上,图3~5比较清晰地展现了Hδ(DB)在所选属性增链上的粒化单调性,这也说明了Hδ(DB)的有效性;对比地,NHδ(DB)由于数值变化较小因而其粒化非单调性表现不是太明显.总之,3个UCI实验较好地说明了新建条件邻域熵的粒化单调性及相关改进性. 基于粒化单调的条件邻域熵,下面说明相关属性约简的有效性.为此,主要在5类UCI数据集(Wdbc,Pima,Sonar,Wpbc,Wine)[21]上实施算法1与算法2,并得到核与约简的最终结果. 针对5类UCI数据集,实验中采用了3种邻域参数,即δ分别取0.3,0.5,0.8.首先利用算法1求出核,再利用算法2求出一个约简(其中属性重要度充当了启发式信息,用以加速整个搜索算法的收敛速度).表5给出了算法1与算法2的具体实验结果,即提供了相关的核与约简;进而,表6给出了相关的数目统计. Table 5 Experimental Results of Core and Reduct Based on Five Types of UCI Data Sets表5 5类UCI数据集上的核与约简的实验结果 Table 6 Number Information of Five Types of UCI Data Sets and Their Experiment Results表6 5类UCI数据集及其实验结果的数目信息 基于表5与表6,这里的数据集已经具有一定规模,但算法1与算法2都能够有效地得到基本结果.下面,针对相同的数据集进行相关分析. 核都在所得的相关约简中,表明算法1的核为约简构建的基础.当然,也有核为空的情况(如Wdbc数据集在δ=0.8时),此时算法2只能直接利用属性重要度进行启发搜索. 基于粒化单调的条件邻域熵,利用算法2可以有效地删除部分冗余属性,保留有效属性.例如,Sonar具有60个条件属性,核包括大约20多个,而约简包括大约30多个,相关属性约简比较合理. 实验结果还依赖于参数δ的取值.随着参数0.3→0.5→0.8的增大,核有扩大或缩小的结果;属性约简一般没有扩大或缩小的变化,但约简基数总体有变小的趋势. 基于大规模数据实验及其结果,本文所构造的属性约简算法是有效的,基于改进条件邻域熵的约简算法可以具体实现,这也充分说明了改进所得粒化单调性的应用价值. 条件邻域熵不具备粒化单调性,其中1个基本诱因是“0概率信息项”未处理导致的信息突变性;从而,粒化非单调性及其诱因阻碍了相关的属性约简发展,例如没法建立约简的核与启发式算法.对此,本文主要进行单调改进与约简构建.通过采用3层粒结构[6],“自顶向下”分解剖析条件邻域熵,“自底向上”集成构建新型条件邻域熵,并在每个层面获取粒化单调性从而实现基本改进.进而,基于高层所建的条件邻域熵及其粒化单调性,深入研究属性约简,并挖掘属性重要度来构造基于核的启发式约简算法(算法2).最后,通过大规模数据实验,有效验证了相关的粒化单调性与属性约简算法.总之,本文所建的条件邻域熵具有粒化单调性,改进了传统条件邻域熵,其诱导的属性约简具有应用前景,但相关的理论探讨与实际应用还值得深入,比如相关的度量保持条件、度量近似应用、与其他约简目标的结合等,度量的分段性还值得实际处理.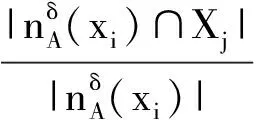
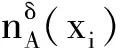
2 基于3层粒结构的粒化单调条件邻域熵



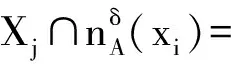
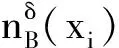

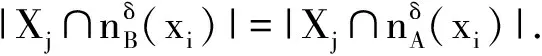
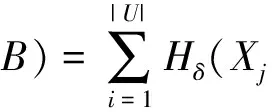
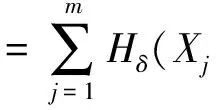
3 基于粒化单调条件邻域熵的属性约简

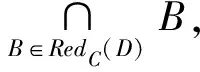
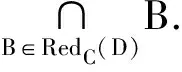
4 UCI数据实验
4.1 改进条件邻域熵的粒化单调性验证
{c1,c2,c3,…,c12};
{c1,c2,c3,…,c8};
{c1,c2,c3,…,c15}.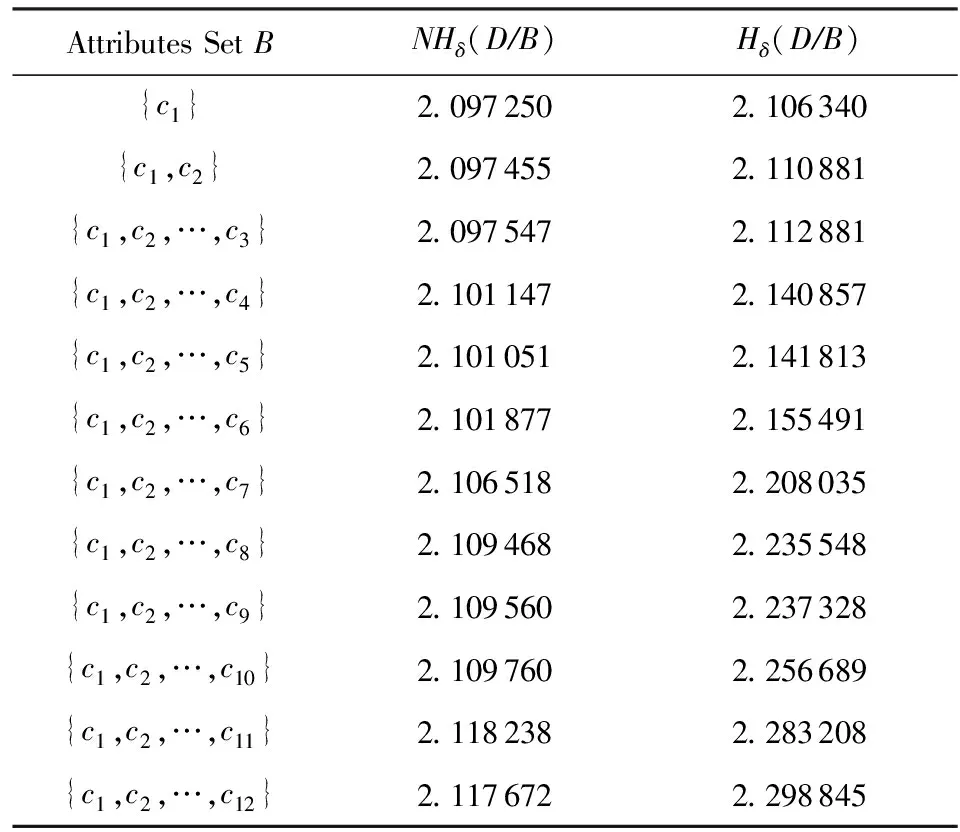


4.2 基于粒化单调条件邻域熵的属性约简实现
5 结 论
