不确定条件下多无人机侦察调度问题*

湛 佳，谢文俊，郭 庆，毛 声

（空军工程大学装备管理与无人机工程学院，西安 710051）

0 引言

多无人机协同侦察将是未来无人机遂行任务的一种重要样式，其核心问题是多无人机侦察调度问题。由于某些待侦察目标出现的时刻具有不确定性和动态性，导致多无人机侦察调度问题十分复杂。最新的研究成果——不确定理论为无人机侦察动态目标问题研究提供了新的理论工具。该理论是对实际应用中的专家信度进行分析的新兴理论，对于先验知识不足、缺乏大量实验样本的问题决策具有重要意义。

文献[1]将任务分配的代价和收益作为总体目标函数，并基于投标过程对任务进行分配。文献[2]对作战时间和飞行距离等指标进行加权，基于攻击任务的最大价值构建了单目标优化问题模型，并采用多子群蚁群算法求解，但忽略了航程的威胁代价。文献[3]基于二进制粒子群算法完成任务分配过程。文献[4]采用整数域改进粒子群优化算法对目标进行分配。人工蜂群（Artificial Bee Colony，ABC）算法其原理是模仿蜂群觅食过程的智能行为，是基于群体的启发式优化算法[5]。ABC算法与差分进化算法、粒子群优化算法和遗传算法相比较，进化的依据为适应度函数，具有控制参数少、操作简单、鲁棒性较强和搜索精度较高等特点，求解质量相对较好[6]。但基本ABC算法存在“早熟”的收敛性缺陷，存在开发能力不足，收敛速度较慢等缺点[7]。文献[8]对传统人工蜂群算法进行改进，提高了算法的收敛速度和全局搜索能力。文献[9]将ABC算法与遗传算子相结合，对可行解进行邻域搜索，算法的搜索能力得到提高。文献[10]设计了一种基于粒子群的ABC算法，通过将全局搜索和局部搜索相结合来寻找最优解。文献[11]针对基本ABC算法容易陷入早熟收敛的缺点，改进了候选食物源的生成方法，增强了ABC算法的全局搜索能力。文献[12]将多种搜索策略相结合，不同策略的解通过竞争产生新的解，算法的局部搜索能力得到增强。文献[13]将ABC算法的全局搜索能力和ACO算法的局部搜索能力相结合得到一种ACO-ABC混合算法，以寻求最优解。文献[14]设定最优邻域解仅在多次未更新的情况下才能替换当前解，使有潜力的可行解得以保留。

针对动态目标出现时刻的不确定性，本文在传统人工蜂群算法的基础上，设计了一种改进的双重进化人工蜂群算法。该算法以模型的目标函数作为指引，同时针对适应值函数，在全局搜索中对局部最优解进行处理，利用不同局部搜索算子的优点，加快了算法搜索速度，丰富了可行解的多样性。最后通过仿真实验表明，该算法能在动态条件下完整侦察到所有目标，取得最大侦察收益，并且其调用的无人机数量以及飞行距离最小，使得总飞行代价最小，实验验证了该算法能有效解决多无人机侦察调度问题。

1 多UAV协同侦察数学模型

1.1 问题描述

在战场环境中，存在n个待侦察目标，用0表示基地，相应的数字表示对应的侦察目标，则组成节点集，用dij表示任意两节点（i，j）之间的距离。一个具有同质性的无人机侦察分队K位于基地，每架无人机具有相同的有效侦察载荷量Q。用qi表示每个侦察目标所消耗的侦察载荷量。此外，无人机存在一个续航时间。对于每个待侦察目标i，都存在一个侦察时间窗。在执行任务的每个时间点t，侦察目标分为以下两类：

1.2 收益值计算

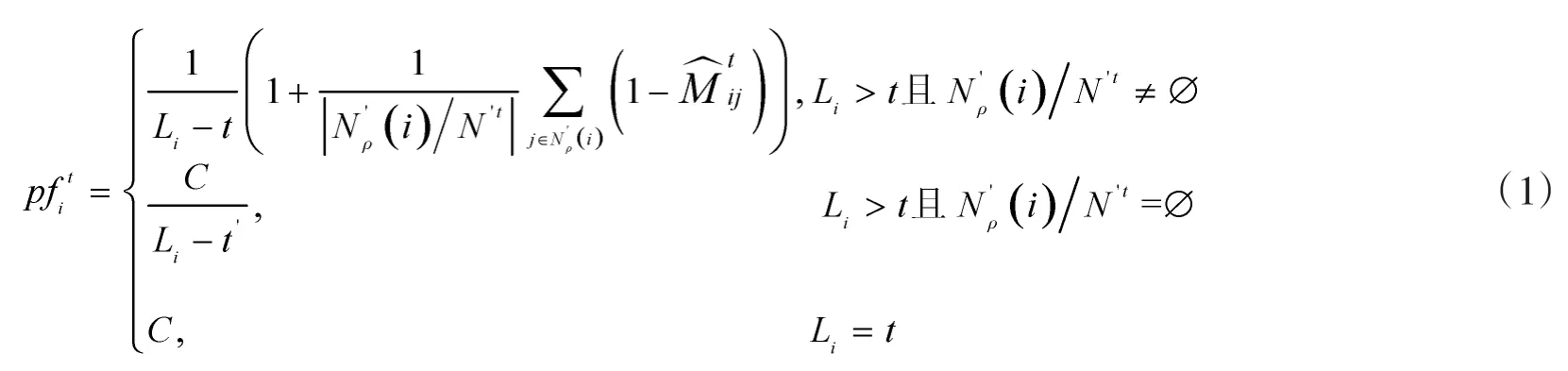
即动态目标j在 ∈[t+1，Li]中所有时刻 出现的信度的和值。

1.3 目标函数

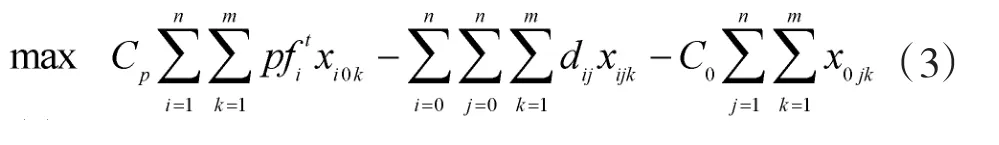
其中，Cp与C0为常数，xijk为｛0，1｝变量，若第 k 架无人机从节点i前往节点j，xijk=1，否则xijk=0，dij为节点i与j之间的距离；目标函数第1项为总侦察收益，第2项为无人机总飞行距离，第3项为无人机固有飞行代价。无人机若能侦察到所有目标，则其总侦察收益最大，若完成侦察任务所调用的无人机数量及其飞行距离最少，那么目标函数的总飞行距离以及固有飞行代价最小，所以优化的总目标在于利用最少数量的无人机和最小化飞行总里程完成侦察任务。

1.4 约束条件

无人机对单个目标至多完成一次侦察，其约束条件为：

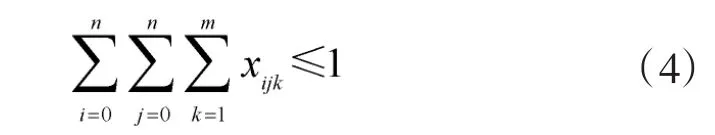
允许无人机在最早可侦察时刻之前到达目标区域，其约束条件为：

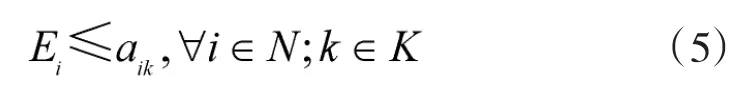
无人机必须在可侦察时间窗结束之前开始侦察，其约束条件为：

为了保证时间连续性，其约束条件为：

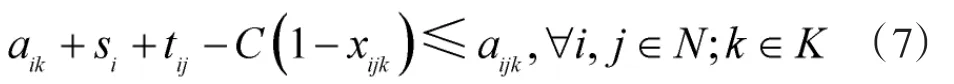
其中，C为足够大的常数，基于第k架无人机到达目标点i的时刻aik，以及该目标点所需侦察时间si，即可计算离开时间；

为了保证无人机从基地出发到第1个目标点的时间连续性，其约束条件为：

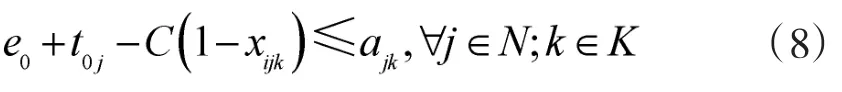
为了保证无人机返回基地的时间连续性，其约束条件为：

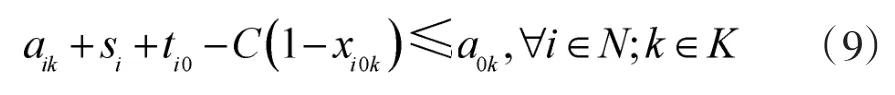
综上所述，每个决策阶段的侦察调度模型如下所示：

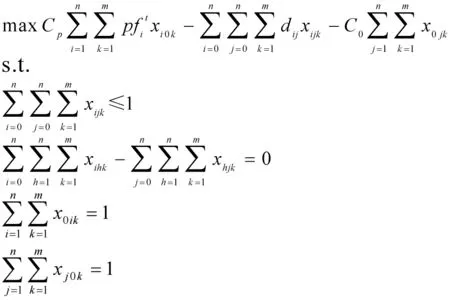
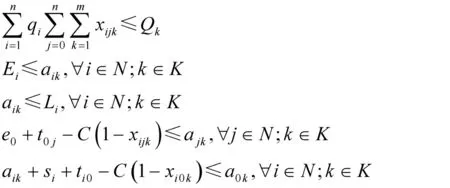
2 调度方案求解

2.1 终止条件

一般条件下，若算法完成了设定的迭代次数，则可判定终止。除此之外，也可以通过判断算法在全局搜索过程中产生的解是否迅速收敛作为算法终止的条件。这种方法可以避免以迭代次数作为终止条件产生的冗余迭代，在动态场景下具有较好的应用效果，缺点是由于迭代次数不够，可能导致算法在全局搜索过程中未能发挥最佳效能。

2.2 解的编码方式

用数字表示相应的目标，其中0表示基地。序列首尾数字均为0，表示无人机从基地出发，再返回基地；数字排列的顺序代表的是无人机执行任务中侦察目标的顺序。将各子序列首尾相接，构成一个完整序列，用此方式来表示一个可行解。各无人机型号不同时，序列中第i个子序列代表第i架无人机的侦察子方案；否则取消这一对应关系，全序列仅表示存在这样的一个侦察方案，以避免冗余。

以15个目标，3架无人机为例，一种可能的调度方案的表示如图1所示。

图1 调度方案示例

为方便文中叙述，用 vk（i）表示第 k架无人机到达的第i个节点，rk表示其对应子序列的节点总数，则该UAV的侦察方案也可用节点集表示，其中初始节点和终止

节点均为基地。

2.3 初始化

1）基地设为v1（1），最低代价设LC为无穷，设置无人机数量上限为#veh，初始化最佳方案序列X=｛v1（1）｝。

4）输出参数集及其对应的最佳方案集。

2.4 适应值

适应值函数fitD按式（10）计算：

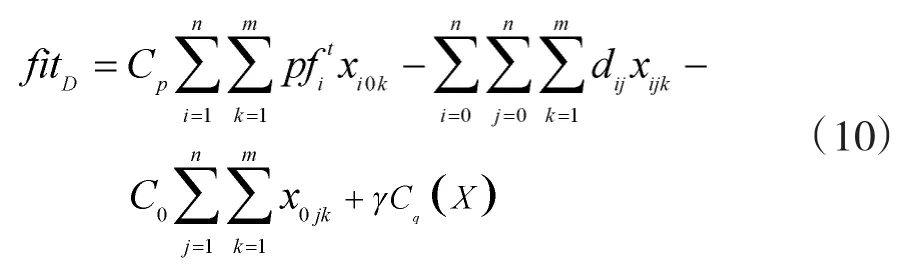
其中，γ为自适应约束系数，在一次局部搜索过程中，γ的值随搜索过程动态变化，若在较优解中，违反载荷量约束解的数目超过总数的一半，则；否则，其中φ为常数。γ越小，对可行解的限制越小，搜索范围就越大；γ越大，对可行解的限制越大，搜索范围就越小。

2.5 选择和跟随

在雇佣蜂阶段进行之后，跟随蜂通过概率pi对雇佣蜂找到的蜜源进行选择，pi根据轮盘赌方法计算，如式（11）所示：

其中，N为解的数量。

2.6 双重进化过程

在跟随蜂和雇佣蜂阶段，该算法均进行了局部搜索，搜索过程中均采用双重进化方法[16]。其具体操作过程如下：

1）半随机式最优插入点算子，如图2所示。

①随机选取插入点r1，插入位置记为r2；

②r2遍历所有可行的插入位置，生成新的可行方案，并计算各可行方案的适应值；

③找到使适应值最小的可行方案，并将r1处的目标插入到该位置。

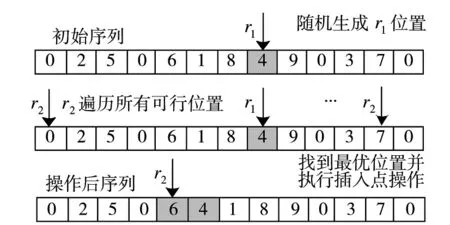
图2 半随机最优式插入点算子

2）半随机式最优逆转序列算子，如图3所示。

①随机选取子序列的一端记为r1，子序列的另一端记为r2；

②r2遍历可行子序列的另一端，将r1、r2确定的子序列逆转，生成新的可行方案，并计算各可行方案的适应值；

③找到使适应值最小的可行方案，并将子序列逆转。

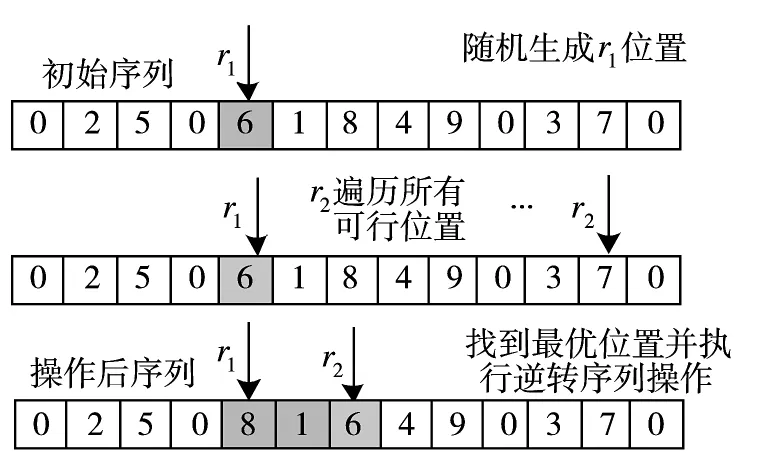
图3 半随机最优逆转序列算子

这一搜索过程较为快速和高效，计算量较小，在文中将其命名为基于重新构建方案的局部搜索方法。

侦察动态不确定目标的多无人机侦察调度方案求解流程如下页图4所示。在目标数据更新之后，优先采用快速局部搜索方法；如果这一方法达到收敛（最优解经过βLimit次迭代未更新），而动态目标仍未出现，则一直采用基于重新构建方案的局部搜索方法，基于待侦察目标集制定当前侦察方案。

3 实验结果及分析

3.1 应用场景想定

本文将UAV对某海域岛礁的侦察监视设定为任务背景，假设基地位于岛礁集群的中点（经度114.60°，纬度9.47°）。各个目标以及目标与基地两两之间的距离通过欧式空间距离确定；具体结果利用高斯坐标转换进行计算，采用是西安1980参考椭球和三度带投影。本文假定，原50个岛礁中，有5个岛礁附近会有非法船只出现，作为动态不确定目标，其基本设置如下页表1所示。

表1中出现时刻所服从的不确定分布是依据已知信息和战场经验估计而来，具体内容为其出现时刻服从的不确定分布；持续时间为对方舰船在争议海域停留的时间。设定飞行速度为144 km/h，飞行单位距离所耗时间为确定值，要求对多无人机进行动态调度，使得无人机使用数量最少，总飞行代价最低，同时尽可能完成所有目标的侦察。

3.2 仿真试验

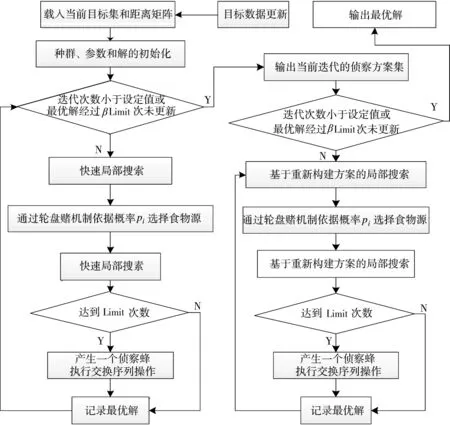
图4 算法流程图

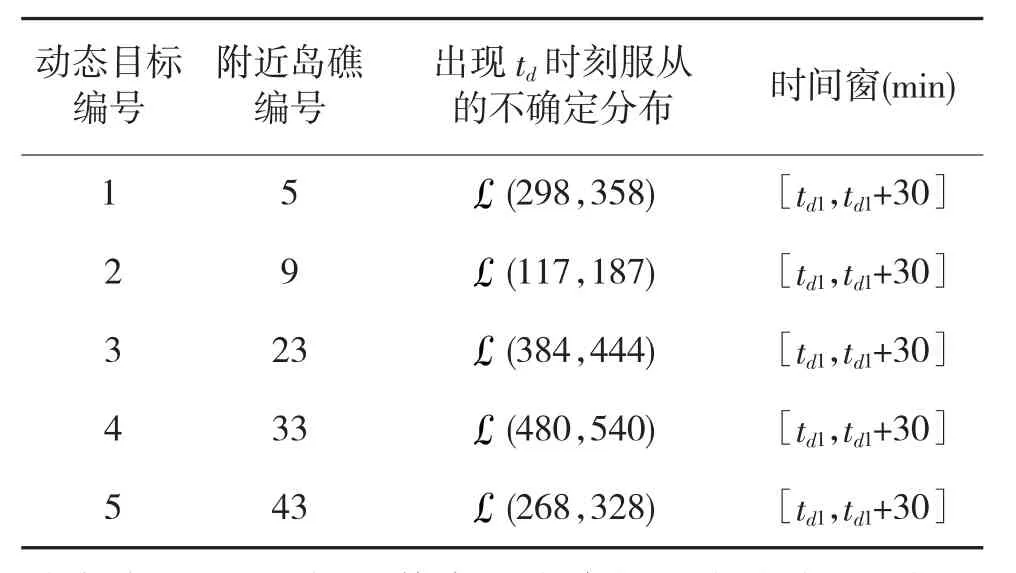
表1 动态不确定目标信息

在UAV执行任务过程中，针对本文设计任务的计算量和搜索深度，在不同的时间紧迫度情况下，结合HB-ABC与RC-ABC的局部搜索策略进行动态多UAV目标的侦察调度求解。实验中，最大循环次数设置为1 000，β的值设定为3，Limit的值设定为20。由于实验中动态目标出现的具体时刻不同，会影响侦察调度方案的指定。故选择其中一种执行的情况，利用STK软件展示如图5所示。从图中可以看出，无人机对所有目标均进行了侦察，其总侦察收益达到最大。

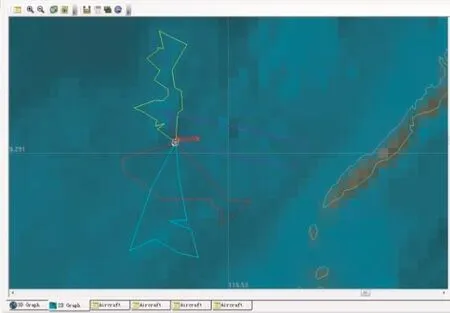
图5 侦察调度方案

为测试将RC-ABC算法和HB-ABC算法局部搜索策略相结合的有效性，分别单独用这两种ABC算法进行跟踪，并与RC-HB-ABC算法比较最终跟踪结果，其中RC-HB-ABC算法中与终止条件相关的参数β取3，且动态目标的权重远大于已知目标。

实验设计两种不同的动态度进行测试，分别为10%，30%；即分别有总数量中10%，30%的目标是决策者在无人机开始侦察时仅拥有专家的不确定知识，而它们并未出现。随机选取C101、C106、R101、R106、RC101、RC106 进行改动和实验，实验中，随机选取原测试数据集中的点作为动态目标点，出现时刻在[0，Li]中生成。对每组动态测试数据，通过30次的运行选取最佳结果，结果如表2与表3所示。

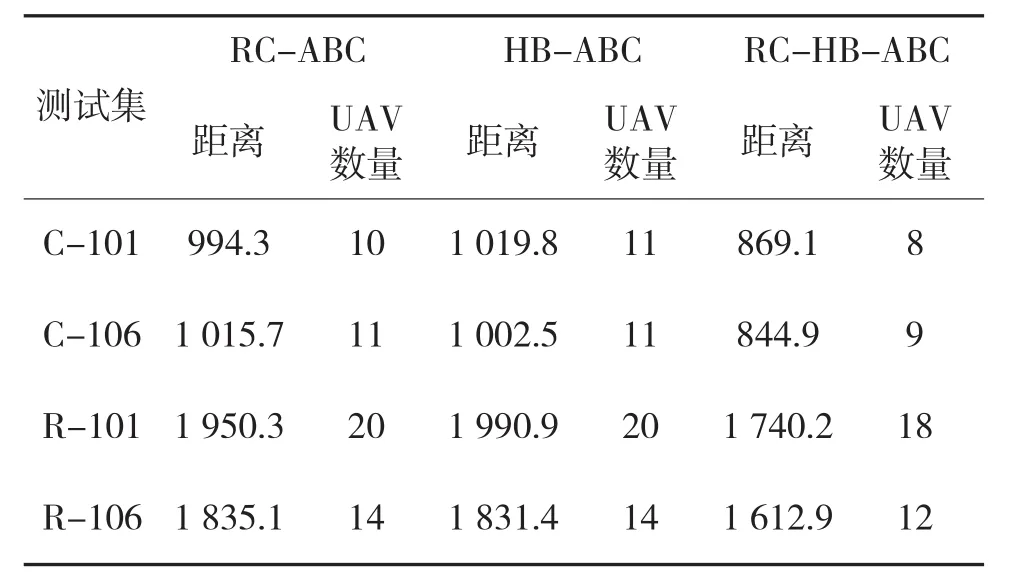
表2 10%动态度下不同ABC算法结果比较

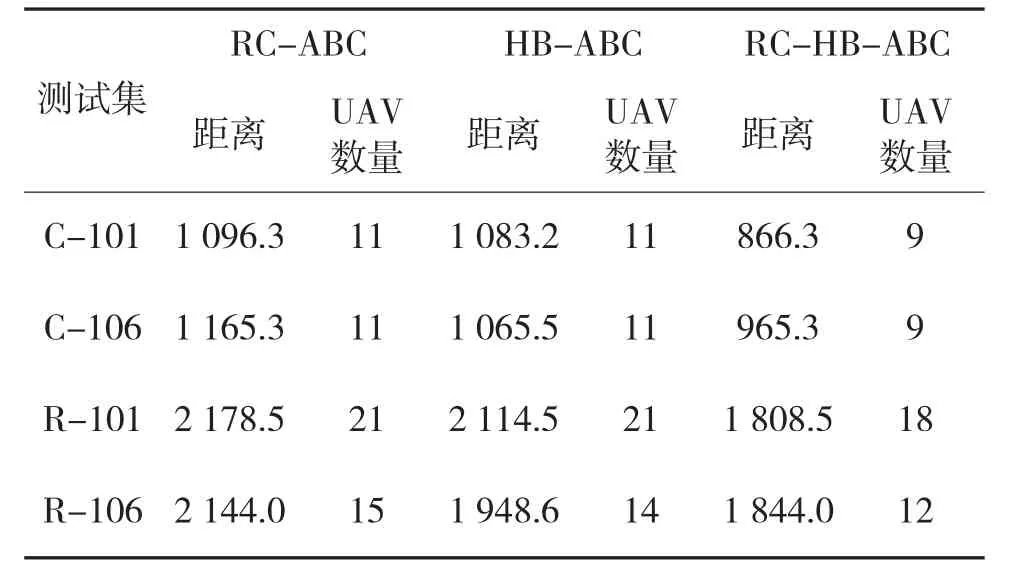
表3 30%动态度下不同ABC算法结果比较

由表2与表3可知，从优化距离的角度来看，将两种策略相结合取得的效果最佳。RC-ABC算法与HB-ABC算法依据测试集动态度的不同，优化结果有差异；但整体上来看RC-HB-ABC算法在动态度测试问题中优化结果相对较好。

为对结果进行具体评估，在10%动态度下，将3种跟踪策略解决R103测试集的收敛曲线展示如图6所示。由图6可知，HB-ABC算法跟踪策略收敛速度较快，但由于搜索深度不够，解的质量相对不是很理想，但在动态目标出现的紧迫度较高时能得到最好质量的解；RC-ABC算法的局部搜索策略能够进行较为深度的搜索，但搜索时间较长，在紧迫度较低的情况下能够得到最好质量的解；RC-HB-ABC算法的搜索策略结合了两种搜索策略的优点，一方面判断使用哪一种具体策略的过程中计算量较小，因此，在时间紧迫度高的情况下收敛速度与HB-ABC的局部搜索策略几乎相同；另一方面在搜索时间较长的情况下，由于是顺次进行两种搜索策略，在某些情况下还能求得比RC-ABC质量更好的解。实验结果验证了所提出算法的有效性以及解决多无人机调度问题的可行性。

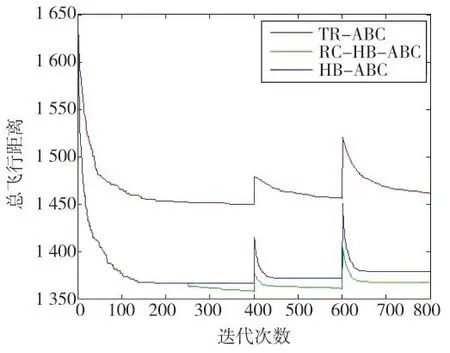
图6 收敛曲线图

4 结论

本文在构建动态环境下多无人机调度问题模型的基础上，设计了一种改进的双重进化人工蜂群算法求解该模型。通过仿真实验，证明该算法能在动态条件下完全侦察到所有目标，取得最大侦察收益，并且完成侦察任务所调用的无人机数量以及飞行距离最短，使飞行代价最小。最后将该算法与RC-ABC以及HB-ABC算法进行比较，实验结果表明该算法能显著提高收敛速度和全局寻优能力。