杂波环境下基于IMM-PSNF的机动目标跟踪算法
2018-11-13马健凯包守亮程水英
马健凯,包守亮,程水英
(国防科技大学电子对抗学院信息处理重点实验室,合肥 230037)
0 引言
对杂波环境下的机动目标进行跟踪,关键在于两点:一是杂波环境下的数据关联问题,二是由于目标机动所带来的状态模型与实际运动模型不匹配问题。数据关联用于在杂波环境下跟踪单目标或多目标,解决点迹与航迹的正确互联[1]。自被提出至今,已经形成了诸多算法:最近邻算法(NNSF)、最强邻算法(SNF)、概率数据互联算法(PDAF)、联合概率数据互联(JPDA)、多假设多目标跟踪算法(MHT)等等。1973年Singer和Sea设计出最近邻滤波器(NNSF),凭借其算法简单、计算量小的优势得以广泛应用[2]。而利用波门中有效量测信号强度最大进行滤波更新的最强邻滤波器(SNF),其算法同样简单有效,但由于不需要计算确认量测到预测值的距离,具有更小的计算量[3]。然而NNSF和SNF都存在同样的问题,认为最近的或最强的量测只来源于目标,过分信任量测使预测波门很小,导致滤波器跟踪机动目标容易发散[4-5]。针对此缺陷,文献[6-7]提出了概率最强邻算法(PSNF)、概率最近邻算法(PNNF),认为应考虑量测来源于虚警的可能以及波门内没有量测的情况。PSNF和PNNF很好地解决了在线计算协方差不准确的缺陷,提高了SNF和NNSF算法的稳定性和精度,但是PSNF要优于PNNF。PDAF是一种全邻滤波器,考虑落入波门内的所有确认量测,利用概率加权构造等效量测进行滤波更新。而PSNF虽是单邻滤波器,但在杂波密度较大的情况下依然能够充分利用幅度信息提高量测选择的准确度,在航迹丢失率和算法复杂度上的表现优于 PDAF[6]。
尽管PSNF、PDAF对非机动目标有较好的跟踪效果,但是对于机动目标,单个运动模型很难准确反映实际目标的运动特征,因此,常常出现目标的丢失和误跟踪。Bar-Shalom和Blom在广义伪贝叶斯算法的基础上,提出了具有马尔科夫切换系数的交互式多模型算法(IMM)[8]。许多优秀的论文已经证明了IMM算法在机动目标跟踪中的有效性[9-10]。因此,将杂波环境下的单模型算法与IMM算法相结合[11]所形成的复合算法,是目前研究杂波环境下的机动目标跟踪的主流算法,其中单目标跟踪算法中以IMM-PDAF最为常见。然而,PDAF毕竟是全邻滤波器,算法复杂度较大;而PSNF作为单邻滤波器,其跟踪效果并不逊于PDAF,可是将PSNF用于机动目标跟踪的算法却很少。
此外文献[12-13]指出,IMM算法用于杂波环境的目标跟踪时,在判决波门的选取上存在不合理性,即各个子滤波器采用各自的回波集合,导致由似然函数计算得到的模型概率可能失效,并提出了综合交互式概率数据关联(C-IMMPDA)算法。文献[14]针对杂波环境下的波门选择问题提出了两级模型概率加权波门技术(TS-MPWG),增强了算法的稳定性,但是该算法只适用于特定的模型。
根据以上分析,本文在证明了最强邻(SN)对量测选择有效性的前提下,充分利用交互多模(IMM)算法对机动目标跟踪的优势,结合基于功率特征的概率最强邻(PSNF)算法,提出了用于跟踪杂波环境下机动目标的IMM-PSNF算法,同时利用文献[15]提出的两级模型概率加权波门技术(MPW-CG),增强滤波器的稳定性。仿真表明,该算法在杂波环境下对机动目标的跟踪精度要高于IMM-PDAF算法,且跟踪性能稳定,航迹丢失率小。
1 概率最强邻(PSNF)
1.1 最强邻(SN)模型的建立
假设目标离散的状态方程和量测方程为

式中,Fk为状态转移矩阵,Γk为过程噪声分布矩阵,Hk+1为测量矩阵。wk、ωk+1是零均值的白色过程噪声和量测噪声,且任意时刻wk与ωk+1是相互独立的,它们的协方差矩阵分别为Qk、Rk+1。
定义最强邻量测z*k在所有确认量测中具有最大的功率a*k,即
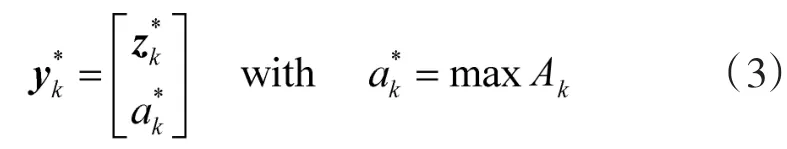
式中,Ak为第k次扫描确认量测的功率集合,且集合Ak中各元素之间是相互独立的。确认量测可表示如下

确认波门采用如下的椭球模型:

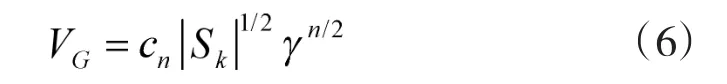
其中,cn是n维单位球的体积,按以下公式计算
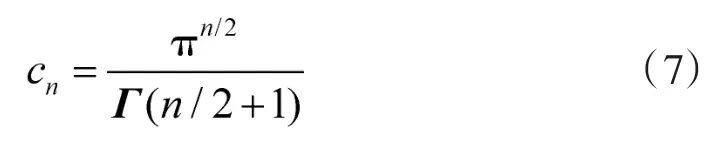
假设确认波门中虚假量测的个数为mF,且mF服从杂波密度为λ的“泊松(Poisson)分布”
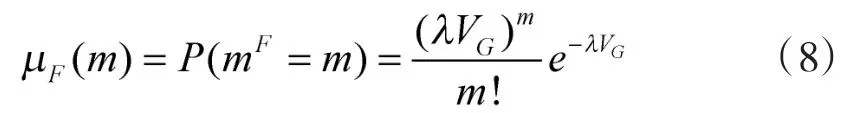
确认波门中真实量测的个数为mT,多数情况下mT=1(真实量测不在波门内mT=0时),先验信息。这里PD为量测超过门限 的概率,PG为源自目标的测量落入确认波门的概率。定义虚警概率为 Pfa,则由下式给出

其中,d代表信噪比(SNR)。来源于真实目标的信号功率服从χ2分布,其概率密度函数(pdf)为

而杂波信号功率的概率密度函数(pdf)为

对各个分量和状态的独立性做如下假设:一个扫描时刻内,虚假量测之间是独立的,在确认波门内服从均匀分布。每个扫描时刻确认量测(真实量测和虚假量测)的功率与位置是相互独立的,与之前任意时刻确认量测的功率和位置也是独立的。
此外,假设目标是存在的,且有一定的概率被检测到。没有检测到存在两种情况:①真实目标量测在波门内,但是没有超过检测门限;②真实目标量测超过门限,但是不在确认波门内。
1.2 PSNF算法
鉴于SNF只考虑最强邻量测来源于目标,一旦选择虚假量测,计算得到的误差协方差就比真实误差协方差小,导致预测波门较小,从而容易产生关联错误,丢失目标的缺陷,概率最强邻算法(PSNF)在此基础上考虑量测来源于虚警以及波门内没有量测的情况。文献[6]证明PSNF要比SNF更稳定,也更精确,而计算量略微有所增加。
在SNF的基础上,PSNF增加了以下3种关联事件:M0为波门内没有量测;MT为最强邻量测来源于目标;MF为最强邻量测来源于杂波。
将波门内没有量测归为第1类事件M0(mk=0),其中;MT、MF归为第2类事件1)。每个扫描时刻根据确认波门内的确认量测数,分两种情况进行滤波更新,算法的具体步骤参见文献[16]。
1.3 PSNF对量测选择的优势
在信噪比d相对较高的前提下,最强邻思想对量测的选择有较大的优势,这也是本文算法的立足点。定义真实目标的信号功率为a+,杂波信号的功率为 a-,则由式(12)、式(13)可以推导出信号功率大
于杂波功率的概率Pa+为
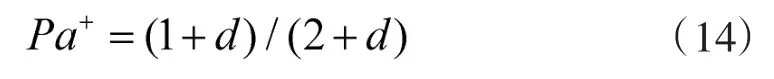
证明过程如下:
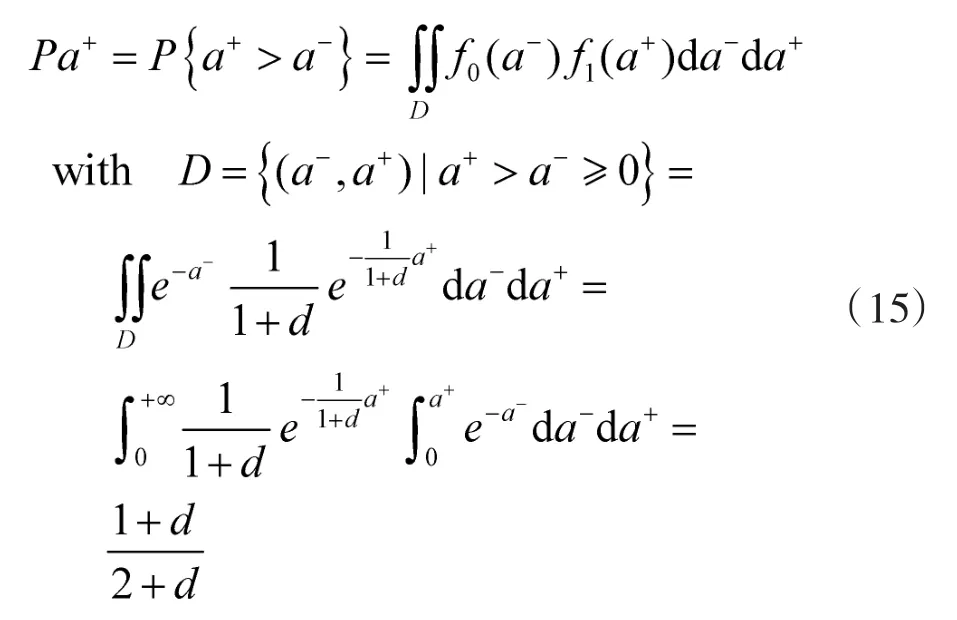
结合目标被检测到的概率为PD,落入确认波门的概率为PG,则滤波器正确选择量测进行滤波的概率PZ为

图1是Pa+、PZ、PDPG随着信噪比d变化而变化的曲线图。不难发现,信噪比在10 dB以上时,目标信号功率大于杂波功率的概率Pa+在90%以上。在d为20 dB的时候,可以达到99%,也就是说,只要真实量测落入确认波门,那么根据最强邻原则,从确认量测中选出真实目标量测的概率为99%;而在全邻滤波器中是将确认波门中所有确认量测进行概率加权,从中可以看出最强邻思想对量测选择的优势。
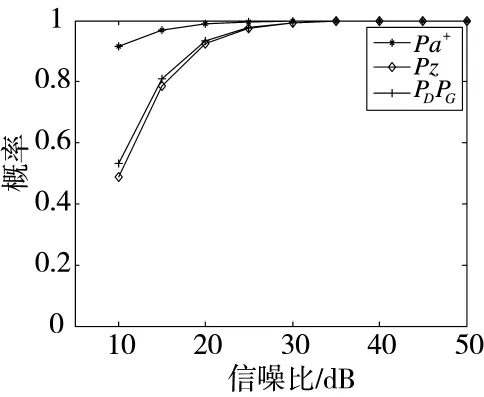
图1 Pa+、PZ、PDPG与 d 的关系
其次,图1中的另外两条曲线分别是PZ、PDPG随d的变化情况,PDPG是真实量测落入确认波门的概率。在全邻滤波器中,真实量测以PDPG的概率落入确认波门,然后与虚假量测一起根据位置关系进行概率加权,真实量测获得的加权概率比落入波门的概率要小,而PZ在目标机动的时候,真实量测将偏离预测值,造成真实量测的加权概率进一步减小;而是PSNF在一个扫描时刻选中真实量测进行滤波更新的概率,易见,它与真实量测落入波门内的概率是很接近的,从这也可以看出最强邻选择量测的有效性。
2 IMM-PSNF算法
图2是本文提出的算法流程图,首先进行模型输入交互,并进行一步预测。根据各模型的回波关联情况,利用两级模型概率加权技术构造统一的波门。然后判断波门中是否有量测,如果没有量测,按照PSNF的第1类(①)事件,即M0情况进行滤波更新;如果有量测,则选择最强的量测,按照PSNF的第2类(②)事件,即情况进行滤波更新。

图2 IMM-PSNF算法流程图
2.1 两级模型概率加权波门(MPW-CG)
杂波环境下的机动目标跟踪,波门的选取是关键问题之一。波门尺寸的大小决定了确认量测数mk。波门太小,目标发生机动时,航迹丢失率很高;波门太大,确认量测中虚假量测增多,计算量增加,跟踪精度降低。同时,在IMM算法中,各子滤波器若采用不同的回波集合,则用似然函数计算得到模型概率可能失效[12],需要使用统一的波门。因此,在基于IMM算法的杂波环境下的机动目标跟踪,确认波门的构造直接影响算法的计算量和精度。本文选择的两级模型概率加权波门(MPW-CG)利用的是中心门(CG)比概率加权门(MPW)大的特点,首先判断概率加权波门中有无量测,若没有,再判断中心波门中有无量测。两级模型概率加权波门,具有效率高、自适应性强,且复杂度不高,文献[15]通过一系列仿真证明了其有效性。
2.2 IMM-PSNF算法步骤
基于交互多模的概率最强邻算法是在交互多模的基础上,将卡尔曼滤波部分用概率最强邻算法(PSNF)代替,其他部分与标准的IMM算法相同。需要注意的是,在滤波更新时,计算确认波门体积使用的协方差是用两级模型概率加权技术得到的协方差Sk,以保证确认波门的一致性。假设目标的运动模式之间的转换是马尔可夫过程,且给定从模型i转换到模型j的转移概率为πij(本文使用3个模型),即

IMM-PSNF的算法步骤如下:
1)模型条件重初始化
首先计算混合概率
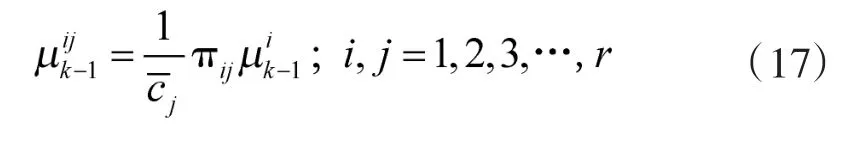
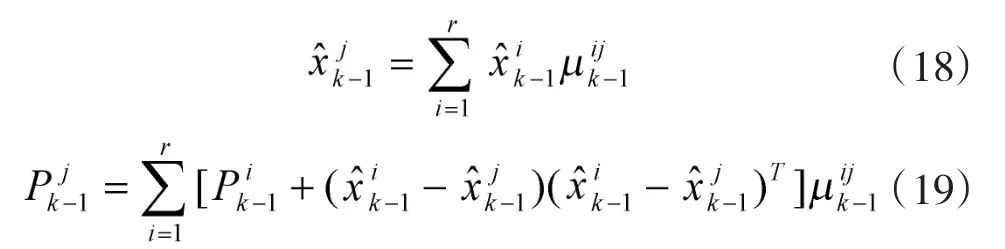
2)模型条件滤波
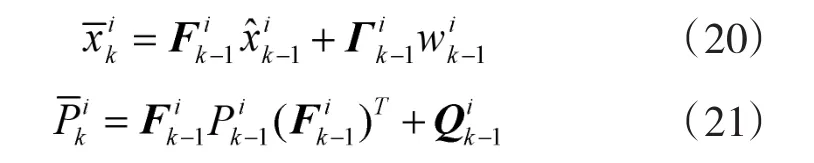
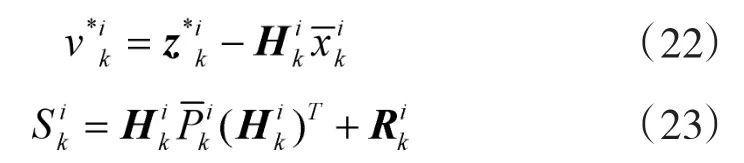
在高斯假设下,计算似然函数

滤波更新先计算混合协方差Sk[14],判断确认波门中确认量测情况,同时求出确认波门体积VG。假如第1类事件发生,即波门内没有量测,则将一步预测值当作该时刻的真实值进行更新,表达式如下
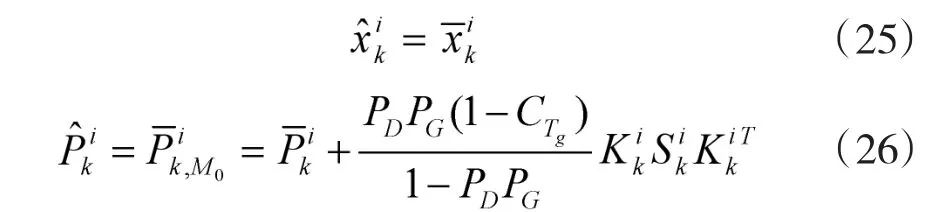
式中,Kik是卡尔曼滤波增益。
假如第2类事件(M0)发生,更新滤波过程如下:

③模型概率更新
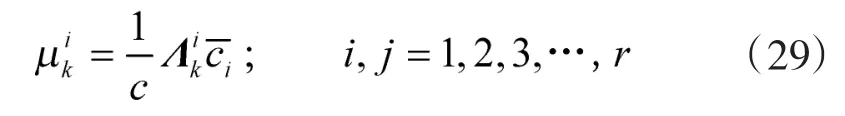
④估计融合

注意:每一个子滤波器利用概率加权波门内的最强量测z*k进行状态更新。
3 仿真结果与分析
3.1 仿真场景及参数设置
选择文献[17]中第6个典型的机动目标运动模型:初始速度为426 m/s,在高度为1.55 km的水平面上运动。运动时间为188 s,采样时间间隔取1 s,其运动轨迹及跟踪效果如图3所示。量测噪声协方差,γ=16,过程噪声分布矩阵,测量矩阵。IMM算法采用CV、CA、CT3个模型进行交互,Markov概率模型转移矩阵,其过程噪声标准差分别为 0.1 m/s2、15 m/s2、10 rad/s2,这里采用的是转弯加速度未知CT模型,转弯加速度标准差为10 rad/s2。如果某次采样时刻估计误差超过量测噪声的10倍,则认为航迹丢失[4],并以此统计航迹丢失率η。
3.2 仿真结果及性能分析
采用本文提出的IMM-PSNF算法对仿真场景中的目标进行跟踪,为体现算法的有效性,与之相比较的IMM-PDAF算法同样利用了两级概率加权波门技术。算法的模型初始概率。
图4和图5分别是信噪比为16 dB,杂波密度λ=10-7个m/s2情况下,做100次Monte Carlo仿真实验的位置和速度均方根误差曲线。由图4可以看出,本文提出的IMM-PSNF算法在跟踪机动目标时,收敛速度较IMM-PDAF算法快,且跟踪精度要高。这主要是因为PDAF是用位置参数进行加权,目标发生机动时,真实量测容易偏离预测值,从而使得对杂波的权值加大,而真实量测权值减小,造成跟踪精度下降。PSNF采用的是功率加权,目标信号强度在统计意义上比杂波信号强,只要真实量测落入确认波门,就能有效选择真实目标量测进行滤波更新,故跟踪精度较高。
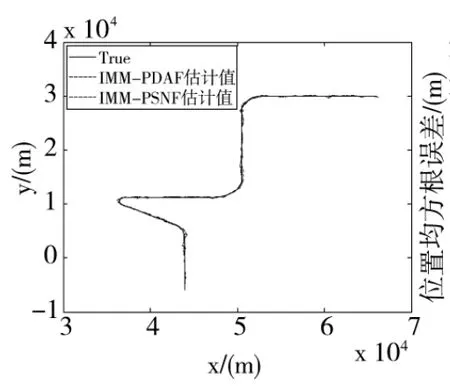
图3 运动轨迹和跟踪效果图

图4 位置均方根误差曲线
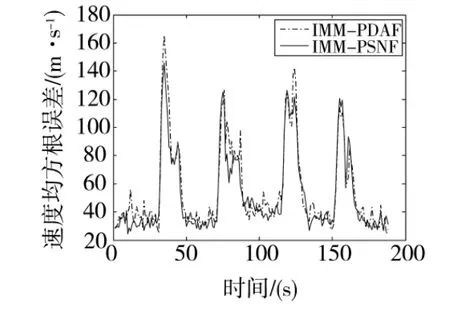
图5 速度均方根误差曲线

表1 航迹丢失率
表1是在不同信噪比条件下,改变杂波密度统计出的航迹丢失率η。该表是1 000次Monte Carlo仿真实验的统计结果。容易看出,IMM-PDAF算法在跟踪机动目标时航迹丢失率较高,而且随着杂波密度λ的增大,航迹丢失率η迅速上升。而本文提出的算法航迹丢失率较低,对杂波密度λ的改变也不敏感。这是因为在杂波密度上升时,波门内确认量测数mk增加,PDAF对每一个量测进行加权,真实量测的权系数进一步减小。而对PSNF而言,杂波强度超过信号强度仍然只是小概率事件,因此,对航迹的丢失影响不大。对于不同信噪比条件下,信噪比下降导致航迹丢失率增加,主要是因为检测概率PD随信噪比SNR的降低而减小。
4 结论
本文针对现有算法在跟踪杂波环境下的机动目标时,随杂波密度的增加,滤波器容易发散且算法复杂度较大的问题,提出将PSNF算法与IMM算法相结合的IMM-PSNF算法。理论分析表明,IMM-PSNF之所以有较好的跟踪效果,是因为其对目标量测的选择具有较大的优势,只要目标量测落入确认波门,就有很大概率被选择用于滤波更新,因此,对杂波密度的变化不敏感,能较好地适应杂波密度变化的环境。仿真结果表明,由于最强邻思想对量测的有效选择,IMM-PSNF不仅跟踪精度比IMM-PDAF高,其航迹丢失率也远远小于IMM-PDAF,且计算复杂度低,具有一定的实际应用价值。
