纯电动汽车驱动桥模态分析
2018-11-11张爽陈长征
张爽, 陈长征
(沈阳工业大学机械工程学院,沈阳110780)
0 引言
随着全球汽车的不断递增,能源短缺和环境污染成为不可忽视的问题,纯电动汽车 (Pure Electric Vehicle,PEV)通过电池带动电动机实现汽车的驱动,保证了噪声低,功率高,与传统的内燃机汽车相比较,在环境保护方面优势巨大[1]。纯电动汽车在各国大力发展和大面积应用,对实现节约能源,保护环境起到了重要作用[2]。电动汽车的噪声振动舒适度等因素对电动汽车的整体评价影响极大。电动汽车承受来自地面传到驱动桥的振动,因此纯电动汽车电驱动桥的固有振动频率和振型是研究汽车振动以及舒适度的重要因素,模态分析技术是研究结构体固有特性的一种方法,对分析纯电动汽车驱动桥的固有频率和振型是必不可少的[3]。
本文利用SolidWorks对纯电动汽车驱动桥进行三维建模,通过ANSYS Workbench中的模态分析模块对驱动桥模型进行分析,提取它的前6阶固有频率和振型,然后再利用试验模态分析方法对纯电动汽车驱动桥实体进行分析,比较两种方法获得模态参数的同异,肯定了有限元方法获得参数的正确性;再将获得的模态参数与外界激励耦合情况进行研究,为进一步研究纯电动汽车驱动桥的动态特性打下基础。1 模态分析基本理论基础
模态分析是研究结构动力特性的一种方法[4],对驱动桥进行模态分析可以确定其固有频率和振型。模态分析所得的参数为进一步对振动系统进行动态设计和故障诊断提供有力的数据支持。
对于一个具有n个自由度的线性系统而言,其振动方程可表示成
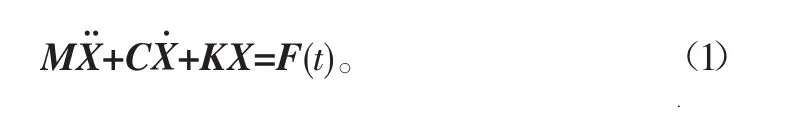
由于驱动桥的阻尼系数较小,在做模态分析时,可以不考虑阻尼,模态是结构的固有特性[6],外载对其不产生影响,所以式(1)可以简化为

设上式的解是

A是幅值向量。
将式(3)代入式(2)得

要使A有非零向量解,则系数行列式必须是零,即
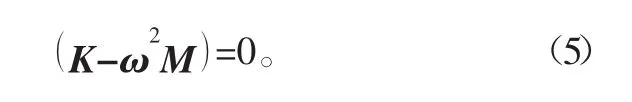
式(5)是关于ω2的n次方程。求出方程n个特征值第i个特征值的平方根ωi便是系统的第i阶固有频率。
令A(i)表示与ωi相对应的振型向量,将ω2i代入式(4)得
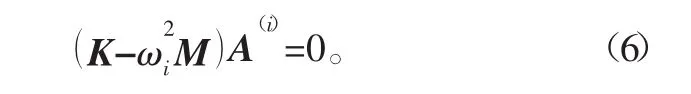
令i=1,2,…,n,可得出n个向量方程,便可求出n个主振型A(1),A(2),…,A(n),至此,可知n个自由度系统对应的n阶固有频率和模态[8]。
2 纯电动汽车驱动桥的有限元模态分析
2.1 纯电动汽车驱动桥的三维模型建立
纯电动汽车驱动桥是纯电动汽车的动力输出构件,将驱动电动机、行星减速器和行星差速器集成在驱动桥壳内,具有驱动和输出同轴,减轻产品的总体质量,降低自身的振动与噪声等优点,同时也提高了驱动桥的可靠性。根据企业提供的数据,通过三维软件建立驱动桥的三维模型如图1所示。然后将建立好的驱动桥模型以x_t文文件保存。
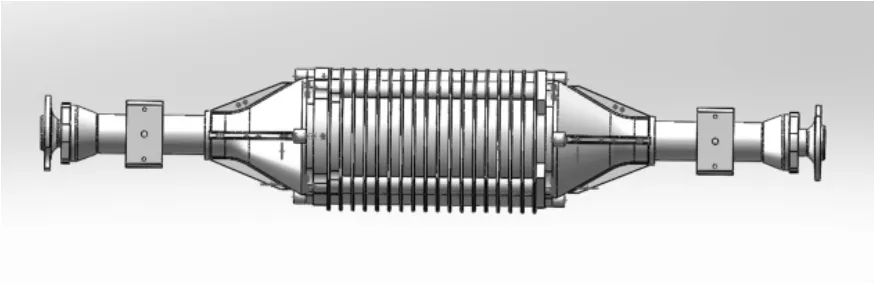
图1 驱动桥的三维模型
2.2 基于ANSYS Workbench纯电动汽车驱动桥模态分析
将驱动桥的三维模型导入到ANSYS Workbench中的modal模块中,首先对模型进行参数设置,根据企业提供的驱动桥各个部件的材料信息,了解到纯电驱动车桥的电动机机壳材料是ZL104,端盖的材料是Q7450,半轴套管的材料是40Cr,分别对各部件进行设定。

图2 驱动桥模型的网格划分结果
在设置好驱动桥的材料属性后,对模型进行网格划分,针对每个不同的部位,使用不同的划分方法,关键部位网格需要密集一些,划分结果如图2所示。
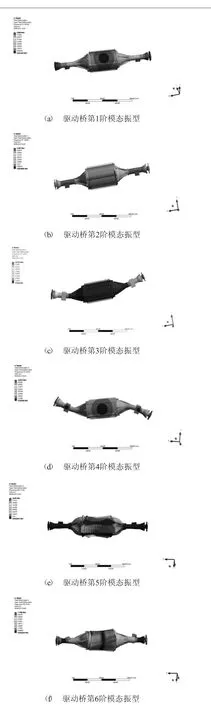
图3 驱动桥前6阶模态振型
对模型网格划分后,使驱动桥处于无约束的自由状态下,获得驱动桥的前6阶模态固有频率及其的振型,如图3示是前6阶模态振型,计算获得的6阶模态频率如表1所示。
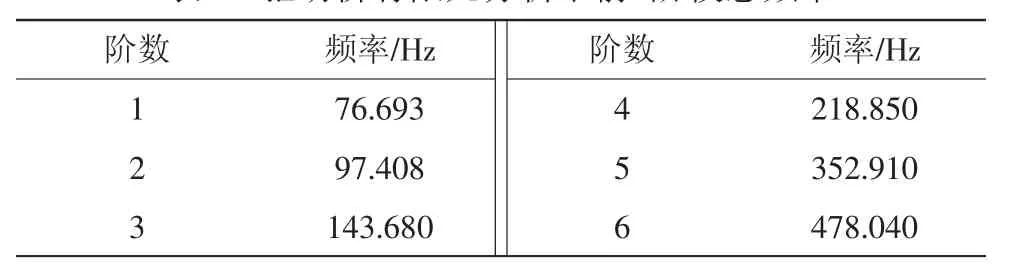
表1 驱动桥有限元分析下前6阶模态频率
3 纯电动汽车驱动桥的试验模态分析
根据纯电动汽车驱动桥的实际情况,将驱动桥通过弹性绳悬吊,布置好激振点和各个测点,然后连接试验所需测量仪器,运用力锤对驱动桥进行多次敲击获得试验的模态数据,获得的试验模态数据图如图4所示,试验得到的前6阶固有频率值与有限元模态分析的结果对比如表2所示。

图4 试验模态数据图
由表2中结果可知,驱动桥的有限元模态频率与测得的试验模态频率都不相同,但差别不大,经过计算,偏差在所允许的误差范围内(15%以内)。证明有限元模态分析的准确性,为进一步研究驱动桥的动态特性做好了准备。
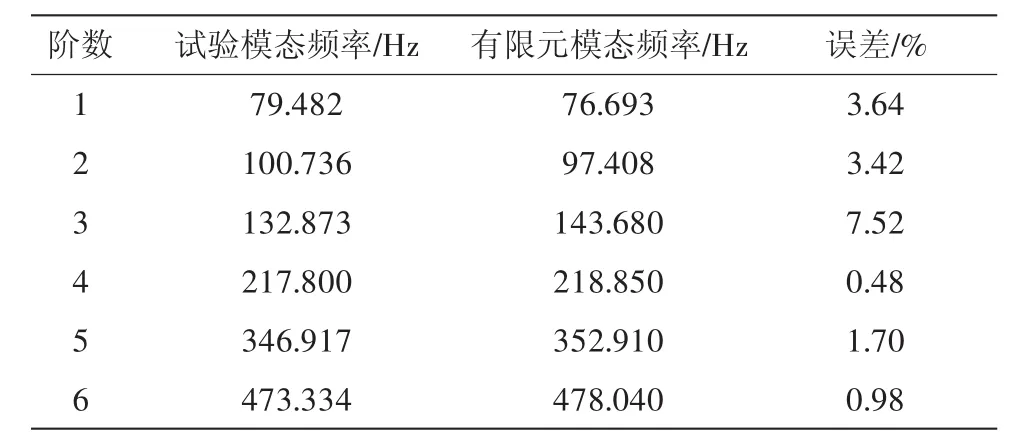
表2 有限元模态分析结果与试验模态分析结果对比
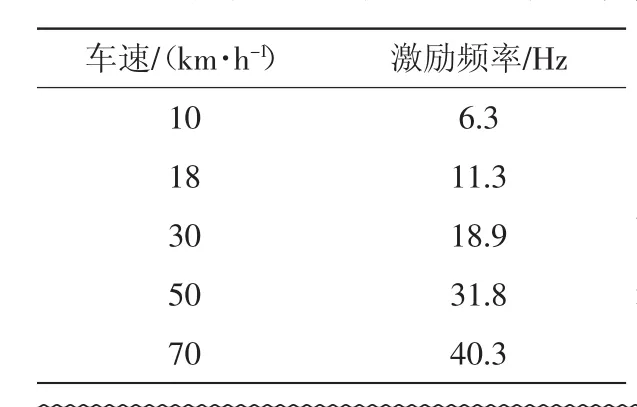
表3 汽车车速对应产生的激励频率
4 与路面激励比较
纯电动汽车行驶在交通公路上时,容易激发驱动桥的弯曲或扭转变形,我们主要应避开纯电动驱动桥与公路路面产生共振或减少振动量值。表3所示是汽车车速对应产生的激励频率。
根据表3可知,电动汽车振动系统承受路面作用的激励多属于0~50 Hz的垂直振动,通过上文的试验模态分析,得到驱动桥固有频率的范围为79~475 Hz之间,由于驱动桥前几阶模态固有频率不在此范围内,因此不会因为路面的激励引起驱动桥的共振。
5 结论
通过有限元模态分析法获得的驱动桥固有特性的结果发现,驱动桥的固有频率在75~480 Hz范围内,在低频状态下驱动桥上下振动,在高频状态下驱动桥扭转振动。本文通过有限元模态分析方法对纯电动汽车驱动桥进行了分析,并且与试验模态分析法相对比,结果表明驱动桥的有限元模态分析法的正确性。通过有限元模态分析以及试验模态分析获得的驱动桥模态参数与路面激励的固有频率相比较,结果显示,驱动桥各阶模态参数都不在路面激励频率内,不会产生共振,保证了驱动桥运行的可靠性。
