螺旋杆桁架式筏架隔振性能研究

张锦光,宋星驰,宋春生,周佳

（武汉理工大学机电工程学院，武汉430070）

0 引言

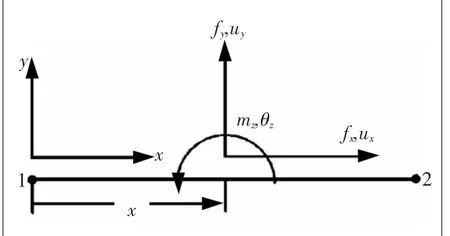
图1 杆件振动模型

潜艇的隐身性能在国防建设中具有重要的战略意义，降低潜艇噪声，提高潜艇隐身能力是海军建设的重要目标[1]。浮筏系统隔振作为一种新型的隔振技术，具有良好的抗冲击能力和稳定性，而且中间筏架具有很大的机械阻抗，可以提高隔振效果，已在舰船上进行了广泛的应用[2-3]。针对筏架结构，研究人员进行了大量的研究，希望可以最大限度地提高浮筏系统隔振性能。孙良贵[4]对四组不同结构形式的中间筏架的物理性能和动态特性进行了分析，给出了几种筏架对隔振效果的测试结果。张衡[5]设计了几种框架板式筏架，得到了组合板具有良好的稳定性和隔振性能。针对海水泵，谢志强[6]设计了一种具有良好的隔振性能的浮筏隔振装置。林立[7]通过对立体框架式浮筏进行研究，给出了浮筏系统的结构设计方法。但传统筏架一般多采用比较简单的板、梁一类的结构，而板梁组成的框架结构的筏架形式比较单一，缺少新的概念，要进一步提高隔振性能存在一定的制约因素[8]。随着近年来对波在周期性结构中传播理论的研究深入，周期性结构筏架被提出。由于桁架式筏架突出的隔振性能，现在已经成为了新的研究方向。Bondaryk[9]对一种桁架结构的舱筏进行了研究，实验结果显示桁架式筏架的隔振效果可以提高到约50 dB。Kohrs[10]研究了多层最小单元格周期性桁架结构的声波传递特性，通过分析无限大轻型桁架梁的振动响应，得到其振动传递的频率通带和禁带的特征曲线。Romeo[11]研究了三重最小单元格周期性结构的波传递特性，得到了几种特定结构的波传递的频率通带和禁带特性。Ruzzene[12]研究了不同最小单元体桁架梁的振动传递特性，对四边形、蜂窝状等最小单元结构的桁架梁在水中的声辐射效率进行了计算。上海交通大学的刘见华[13]研究了波在周期加筋板中的传递特性。程世祥[14]对一种新型周期桁架结构浮筏进行了研究，得到了周期性桁架结构浮筏相对于传统的浮筏结构具有更好的振动抑制作用。本文在前人的研究基础上，提出了一种螺旋杆结构，通过对螺旋杆振动传递特性的研究，设计了一种新型的螺旋杆混合桁架式筏架结构。并且通过仿真分析和实验研究对比分析了新型的螺旋杆桁架式筏架结构和传统的直杆桁架式筏架结构的隔振性能。

1 杆件振动传递力学模型

如图1所示，构成桁架的杆件单元可以当成包含两个平动自由度和一个转动自由度共三个振动自由度的弯曲梁单元处理。

在局部坐标系下，杆件单元的输入参数与输出参数可以表示为：

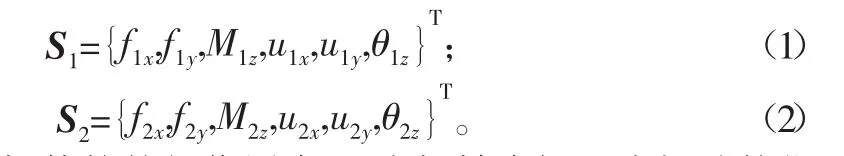
式中：f为杆件的外部作用力；M为扭转力矩；u为振动的位移值；θ为扭转角位移值；x,y,z分别为坐标系的轴向、横向和纵向，1、2为杆件两端点编号。

杆件的弯曲振动方程为：

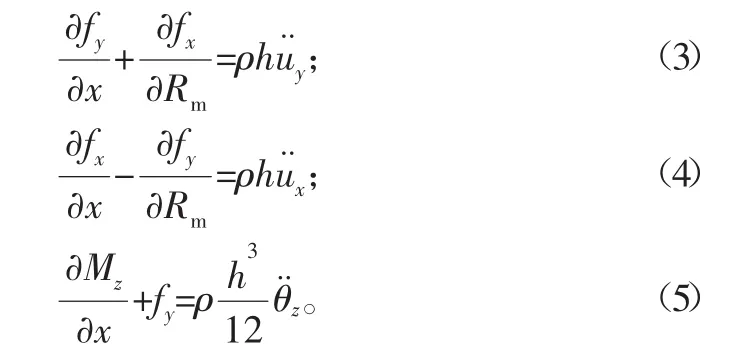
式中：ρ为材料密度；h为横向等效梁高；Rm为弯曲梁曲率半径。

由材料力学，可得下面的关系式：

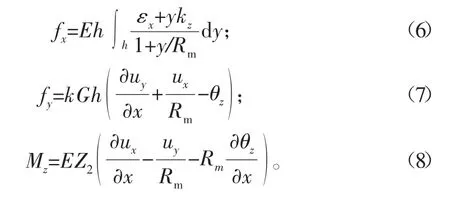
将弯曲振动方程式（3）、式（4）、式（5）和作用力方程式（6）、式（7）、式（8）联合求解得到中各参量微分方程为：

其中：

其中，Z1=h（1+Z*）。简谐激励作用下方程的解为

将式（10）代入矩阵方程（9），得到下式：

由矩阵方程的理论，矩阵方程有非零解的充要条件是系数行列式值为零，即

求解得矩阵方程的特征根为λi，则方程可表示为

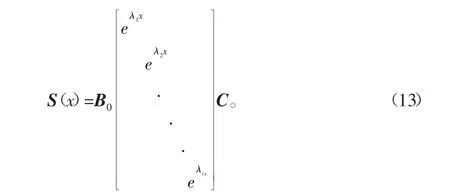
其中，C为系数矩阵，和加载条件有关。

设杆件单元的长度为l，则振动由单元端点1传递到端点2的传递方程式为

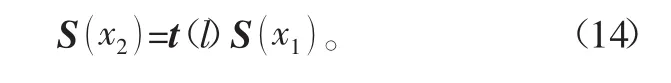
其中，

式（14）即表示杆件单元上的振动传递关系。而一般的桁架都是由杆件组成，如图2所示，桁架最小单元两端一共有4个输入输出点，对比杆件单元结构要复杂，本次每个点上依然取3个自由度。

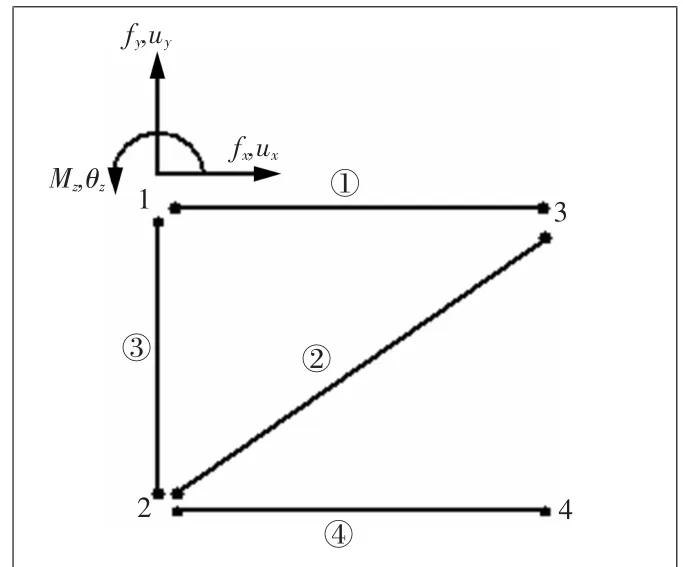
图2 桁架式筏架最小单元振动模型

当最小单元第i个作用点的输入力用{f}i表示，振动速度相应用{g}i表示时，第i个作用点的参数可具体表示为

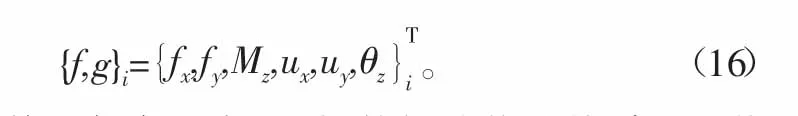
则最小单元任意两点i和j间的振动传递关系可用传递矩阵表示为

式中i、j为1、2、3、4，传递矩阵为

桁架式筏架结构最小单元作用点i、j间的振动传递矩阵关系可以通过有限元计算得

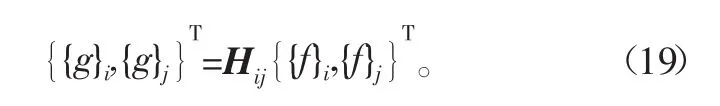
其中导纳矩阵可表示为

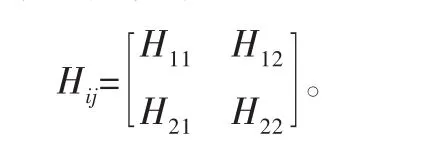
由导纳矩阵方程可以得到输入点i和输出点j的传递矩阵为

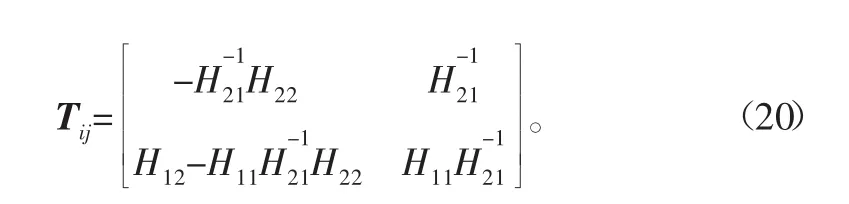
当最小单元体有m个输入点和n个输出点时，传递矩阵可表示为

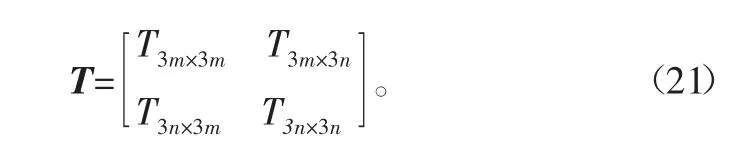
桁架式筏架是由最小单元体串联而成，所以筏架结构的传递矩阵为

2 杆件长度对振动传递的影响

杆件的结构参数主要包含杆件的长度和横截面积，通过保持杆件的横截面积不变，探讨杆件长度的变化对筏架振动传递的影响。建立如图3所示的桁架模型，选取每根杆件的内径和外径分别为5 mm和10 mm，采用接头质量配平的方法来保证整体的质量一样。本文分别选择长度为150 mm、300 mm、500 mm的杆件，研究桁架总长为1500 mm时，不同杆件长度的振动传递性能。桁架结构如图3所示，在1号接头质心处加载1 N的横向简谐激励力，整个结构的阻尼设为0.003，计算另一端点处的振动位移响应，取位移参考值为10-12m（下同）。得到如图4所示的不同杆件长度的振动位移响应值。

图3 桁架模型

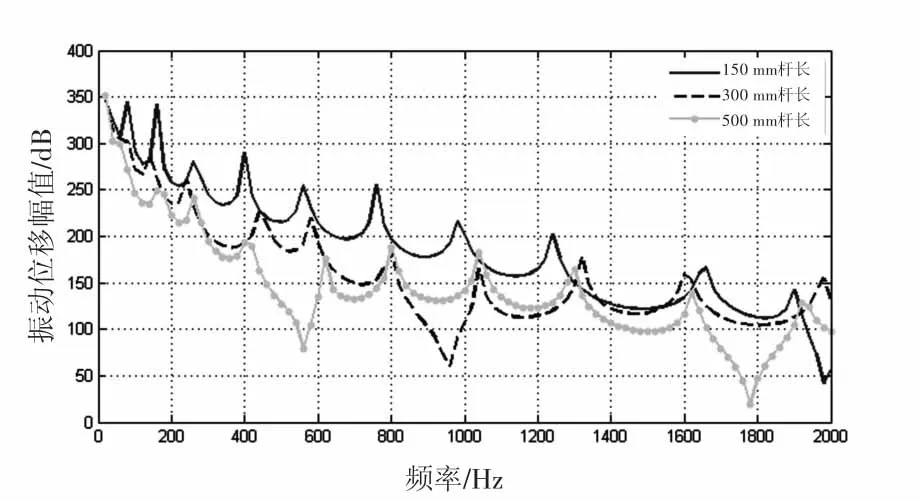
图4 不同杆长振动位移响应曲线

图4表明在0～600 Hz的中低频率范围内，随着杆件长度的增加，桁架对应阶次的振动位移响应值明显减小。理论分析中表明杆件两端点间的振动传递与Rm/h相关，当梁曲率半径一定时，杆件越长振动传递效率越低，与动力学分析结果一致。

3 螺旋杆桁架式筏架振动性能研究

上述研究表明，振动的传递率随着传递杆件的长度变长而减小。当桁架结构两端的距离一定时，螺旋杆结构可以在空间内增大杆件的长度，增大振动传递的距离，因此提出螺旋杆结构，并对其振动传递特性进行分析。

3.1 一维螺旋杆桁架分析

建立总长为1500 mm的一维螺旋杆桁架和直杆桁架，直杆桁架的构成杆长为300 mm,内外径分别为5 mm和10 mm，螺旋杆桁架的构成杆螺距为60 mm,圈数为5,横截面直径为14 mm的螺旋结构。如图5所示，最后桁架的总质量均为7 kg。

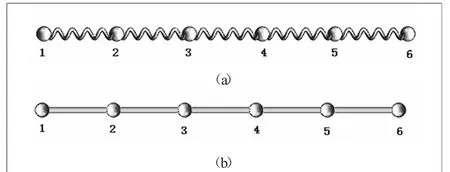
图5 一维桁架

在一维桁架的端部1处加载1 N的横向简谐激励力，在ANSYS中对螺旋杆桁架和直杆桁架进行振动分析，得到另一端部6处的振动位移曲线，如图6所示。

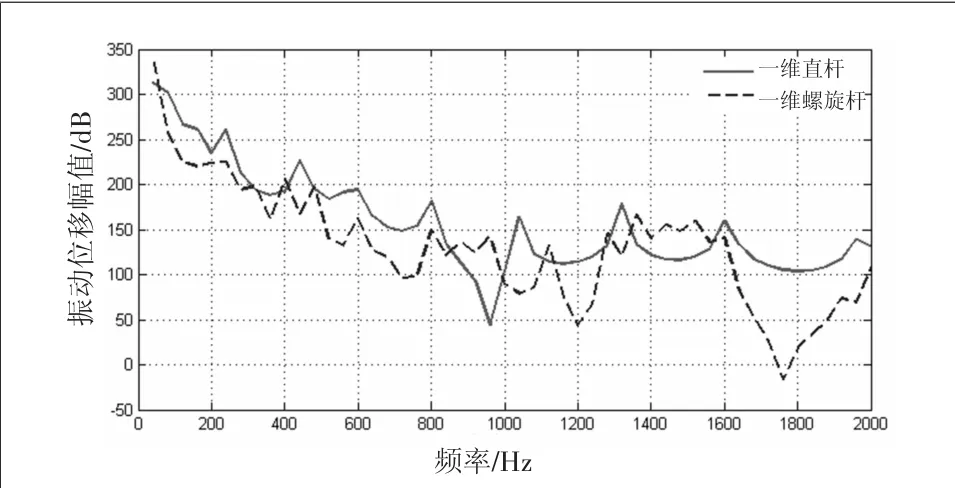
图6 一维桁架振动位移响应曲线

图6显示一维螺旋杆桁架在低频阶段振动位移曲线幅值要明显小于一维直杆桁架，即在低频阶段一维螺旋杆桁架具有比一维直杆桁架更好的隔振性能。当频率增大到800 Hz后，一维螺旋杆桁架的振动抑制能力相较于一维直杆桁架则不如低频阶段显著，但整体上一维螺旋杆桁架振动抑制效果较好。

3.2 二维螺旋杆桁架分析

二维桁架结构如图7所示，每个单元格的尺寸均为300 mm×300 mm,每个接头的直径均为58 mm，螺旋杆和直杆的尺寸均和一维桁架相同。对二维螺旋杆桁架和二维直杆桁架进行振动分析，加载条件和一维分析相同，分析两者的振动传递特性。

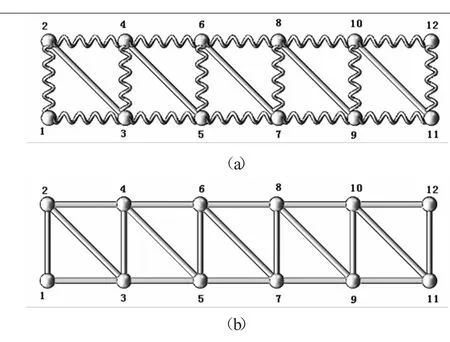
图7 二维桁架

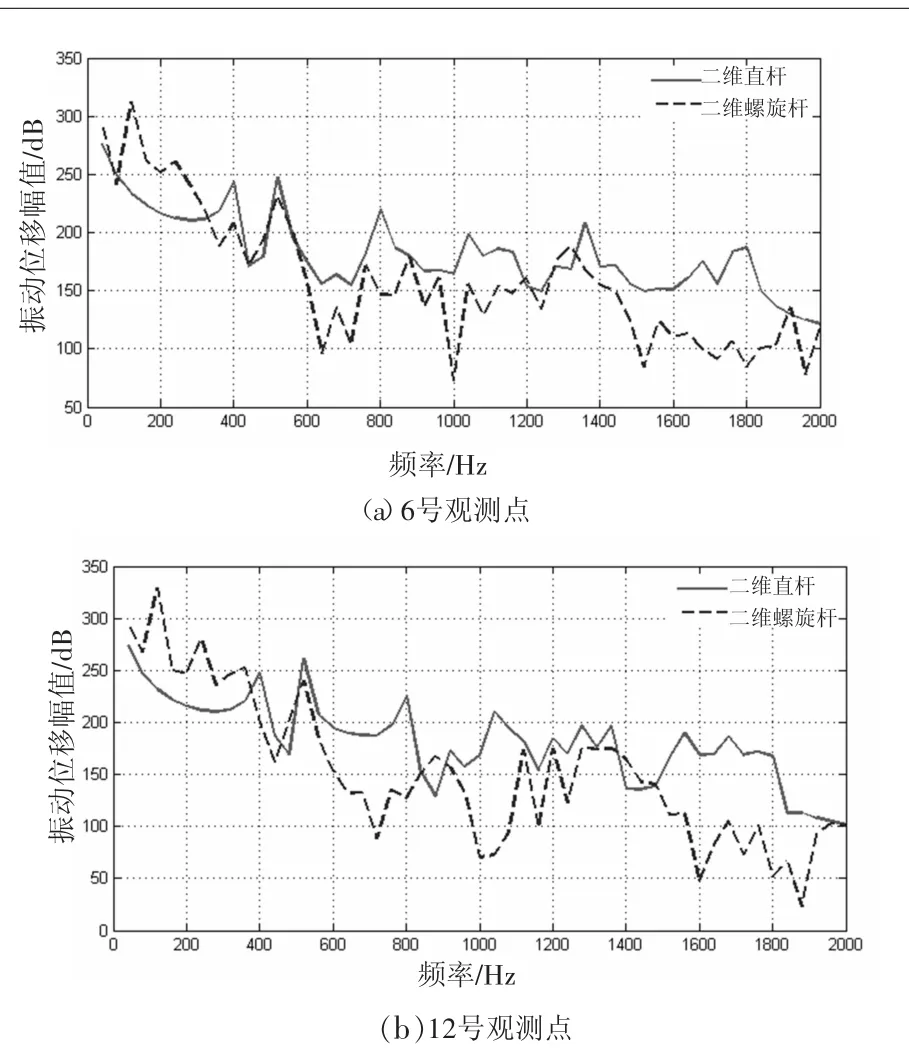
图8 二维桁架振动位移响应曲线

图8给出了二维直杆桁架和二维螺旋杆桁架的振动位移响应幅值对比结果。分析发现，由于螺旋杆桁架的刚度较低，在低频段出现较多的峰值点，导致螺旋杆桁架结构在低频阶段振动传递抑制能力较差。在中高频阶段，螺旋杆桁架的振动传递路径比直杆桁架长，振动的能量损耗更多，因此表现出更好的振动抑制作用。

比较一维螺旋杆桁架和二维螺旋杆桁架的振动传递特性可知，在低频阶段，虽然一维螺旋杆桁架和二维螺旋杆桁架由于刚度较低都具有较多的共振峰值，但在抑制振动传递方面，一维螺旋杆桁架和二维螺旋杆桁架具有较大的差异。一维螺旋杆桁架较一维直杆桁架具有更好的抑制振动传递效果，而二维螺旋杆桁架的振动抑制则明显不如二维直杆桁架。

分析两者结构，二维螺旋杆桁架是由一维螺旋杆桁架通过横向的螺旋杆连接而成，推测是横向和轴向两根螺旋杆之间的相互耦合作用使两者存在较大的差异。本文将横向的螺旋杆换成直杆，进一步分析螺旋杆结构对桁架的振动传递的影响。如图9所示为修改后的二维螺旋杆桁架结构，进行振动分析，得到振动位移幅值对比如图10所示。

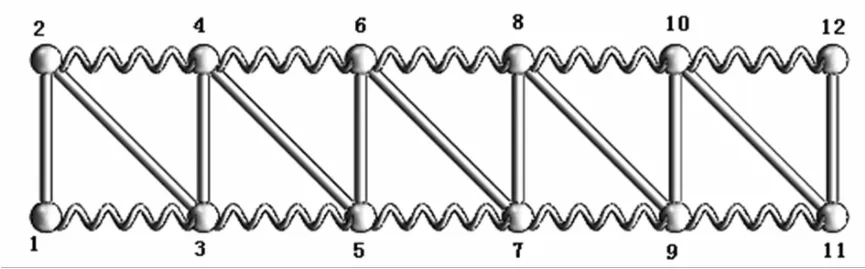
图9 二维横向螺旋杆桁架

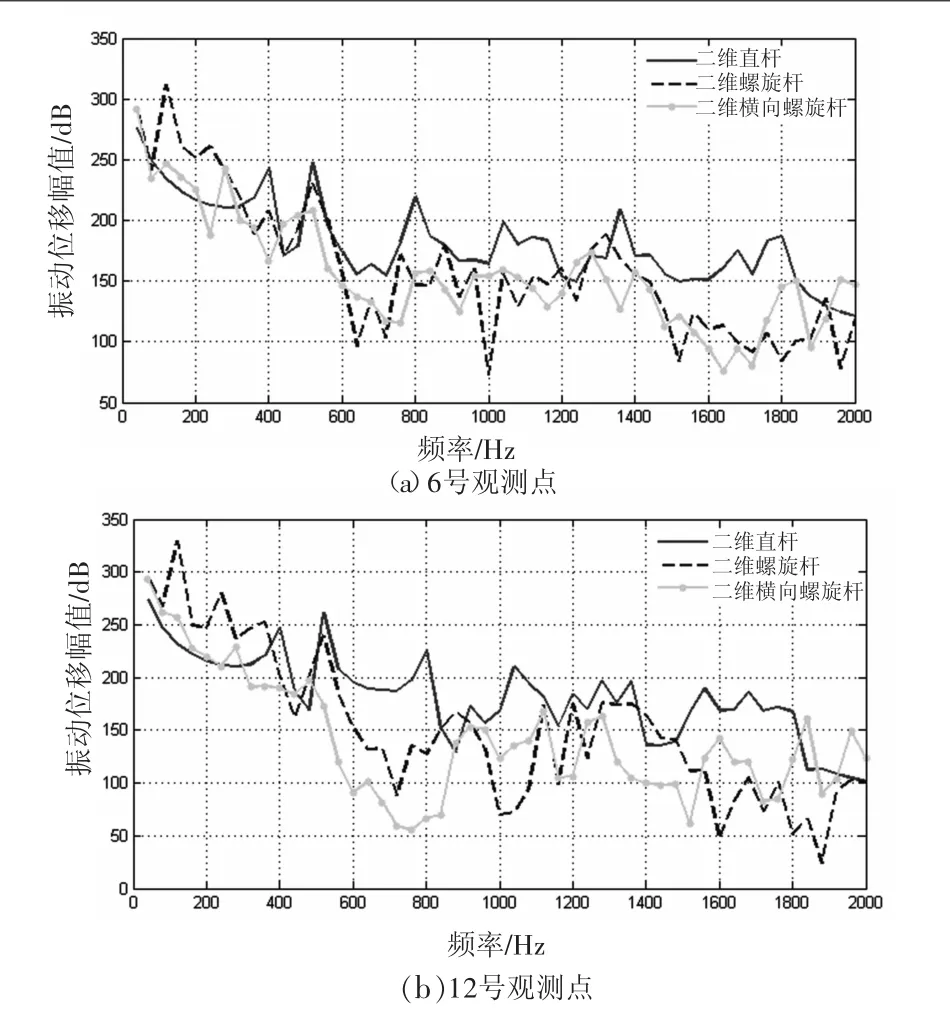
图10 三种桁架振动位移曲线

图10显示，低频阶段，二维横向螺旋杆桁架的振动抑制能力较二维螺旋杆桁架有了明显的提升；高频阶段，虽然二维横向螺旋杆桁架的振动抑制效果相对于二维螺旋杆桁架有所下降，但是对比二维直杆桁架依然具有较好的振动抑制能力，而且随着传递路径的增加，二维横向螺旋杆桁架的优势更加明显。

综上所述，螺旋杆之间存在的耦合作用，使二维螺旋杆桁架的振动抑制能力发生了改变。因此，在设计螺旋杆桁架式筏架时应该尽量避免交叉连接螺旋杆的结构出现，尽量避免在同一最小单元体中出现两根螺旋杆构件。3.3 螺旋杆桁架式筏架的振动传递分析

基于上述结论，设计螺旋杆和直杆混合的桁架式筏架，如图11所示，在一般的桁架式筏架中用螺旋杆代替部分的直杆结构，构造一种新型的筏架。最小单元体均为226 mm×226 mm，直杆的内外径分别为5 mm和10 mm，螺旋杆的螺距取56 mm，球形接头直径均为58 mm,材料均选择普通碳钢。

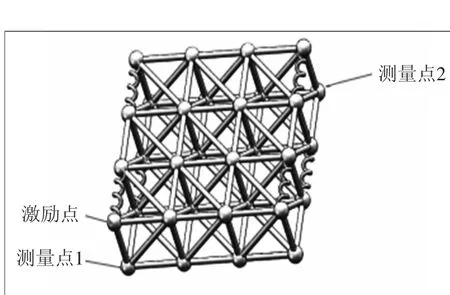
图11 螺旋杆桁架式筏架

分别对直杆桁架式筏架和螺旋杆桁架式筏架结构进行振动分析。分别在直杆桁架式筏架和螺旋杆桁架式筏架的激励点处加载1 N的垂向激励力，计算筏架下底面测量点1和测量点2的振动位移响应。直杆桁架式筏架和螺旋杆桁架式筏架在测量点1和测量点2的振动位移如图12所示。

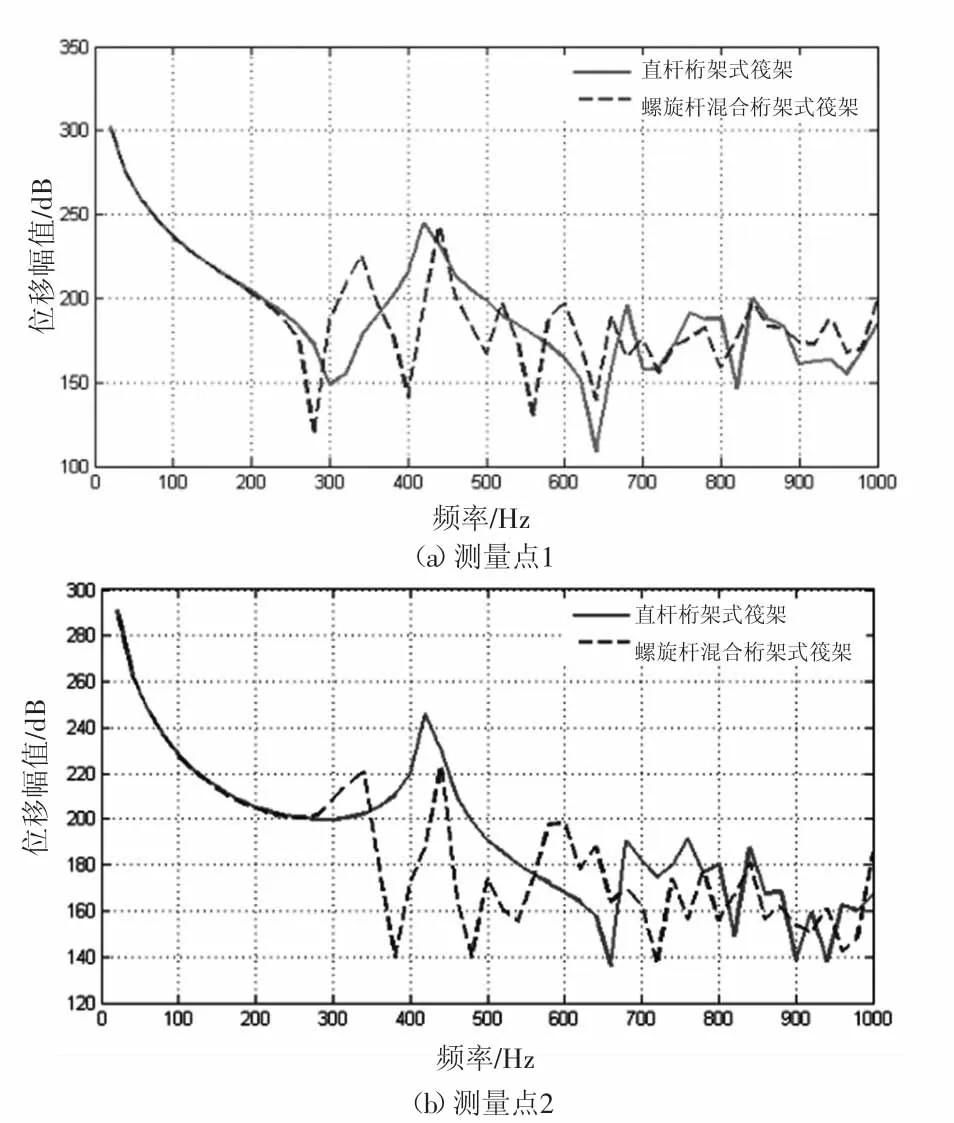
图12 筏架振动传递特性曲线

在0～500 Hz的中低频阶段，螺旋杆桁架式筏架在测量点1和测量点2的振动位移值虽然在较少部分频率范围比直杆桁架式筏架高，但是在整体上，螺旋杆桁架式筏架的振动位移幅值要明显小于直杆桁架式筏架，特别是螺旋杆桁架式筏架的一阶共振峰值要明显低于直杆桁架式筏架。在高频范围，由于筏架表现出整体性，螺旋杆桁架式筏架和直杆桁架式筏架的振动传递区别并不明显。激励点到测量点2的距离较激励点到测量点1的距离长，波传播中损失的能量较多，具体表现为测量点2的隔振效果明显要好于测量点1。因此，引入了螺旋杆结构的螺旋杆桁架式筏架比直杆桁架式筏架具有更好的振动抑制效果。

4 实验探究

浮筏隔振实验系统如图13所示，实验系统主要由振动电动机、橡胶隔振器、桁架式筏架、空气弹簧、基座等组成。电动机分别用4个BE-25隔振器弹性安装在浮筏底部上，筏架再通过4个086060H-1型空气弹簧安装在基座上，基座通过螺栓固定在地面上。为了防止空气弹簧超过行程，筏架和基座之间安装了限位器。电磁作动器的型号为JZK-50，配套使用的功率放大器选用为输出额定功率为800 W的YE5874A。

图13 浮筏隔振系统实验平台

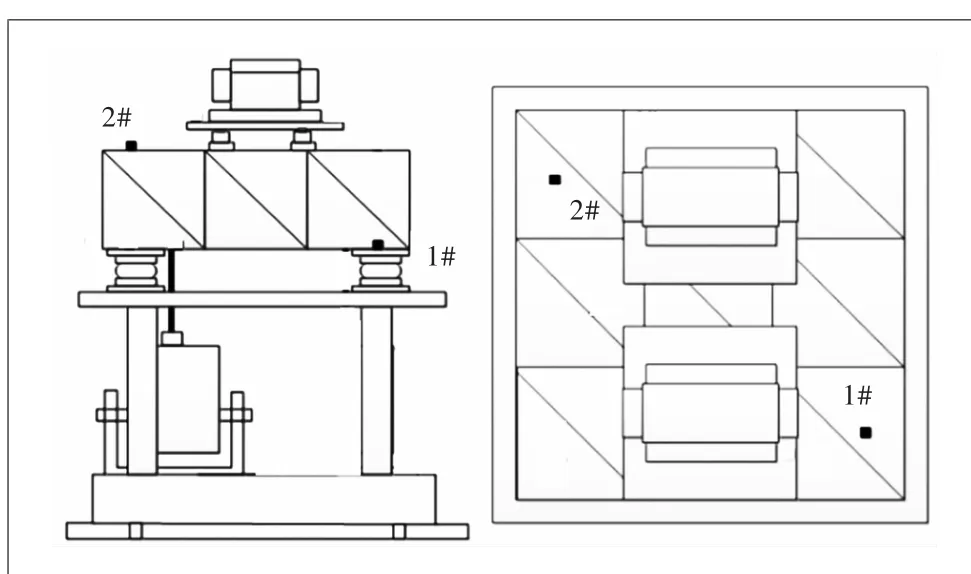
图14 传感器布置图

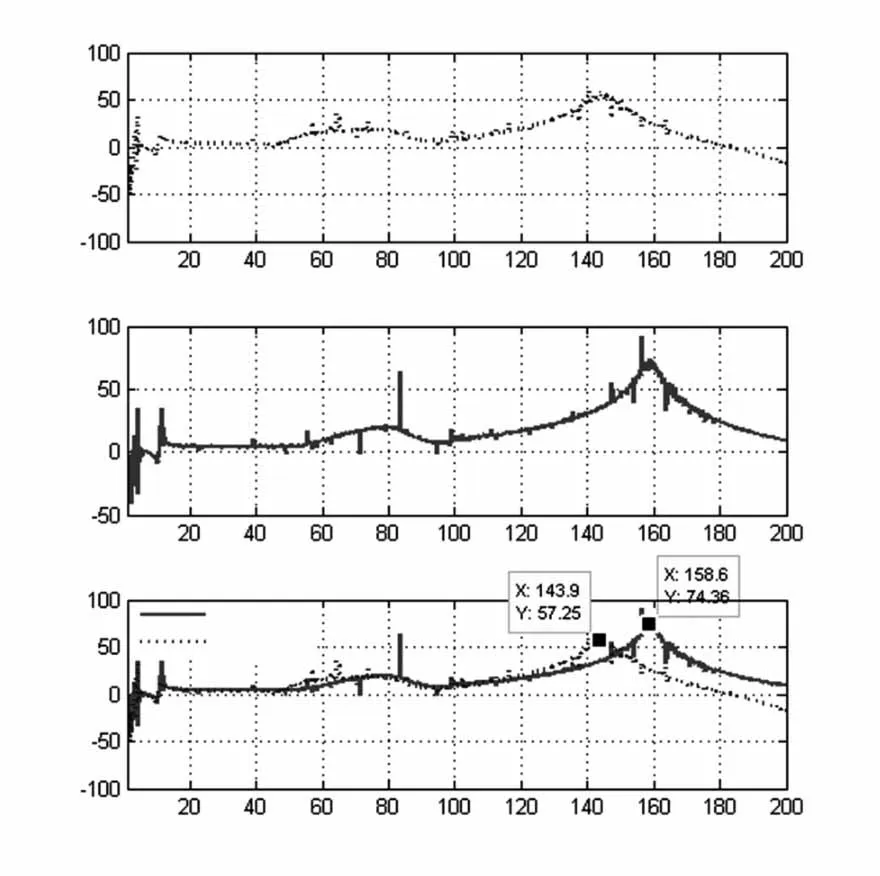
图15 扫频激励下桁架式筏架振级落差

如图14所示，分别布置2个加速度传感器测量筏架输入端、筏架输出端的加速度，然后通过计算加速度振级落差对桁架式筏架的振动传递特性进行评估。本实验采用空气压缩机向空气弹簧充气至0.4 MPa,分别以电磁作动器和两台电动机作为激励源。当电磁作动器为激励源时，电磁作动器和配套的功率放大器输入1～200 Hz的线性扫频信号。此时，1号加速度传感器作为桁架式筏架的输入端，2号加速度传感器作为桁架式筏架的输出端。当电动机作为激励源时，通过变频器控制两台电动机的转速为900 r/min和1200 r/min。此时，2号加速度传感器作为桁架式筏架的输入端，1号加速度传感器作为桁架式筏架的输出端。通过分析1号和2号加速度传感器的振级落差来比较筏架的振动传递效率。

将1号和2号加速度传感器测量的频谱数据，在Matlab中进行处理。图15为电磁作动器作为激励源时的加速度振级落差曲线。对比直杆桁架式筏架和螺旋杆桁架式筏架的加速度振级落差曲线，螺旋杆桁架式筏架隔振效果最大可以达到74 dB,相对于直杆桁架式筏架的57 dB具有较好的隔振效果。

当转速分别为900 r/min和1200 r/min的电动机作为激励源时，如图16和图17所示，分别为直杆桁架式筏架和螺旋杆桁架式筏架的加速度振级落差曲线。表1和表2分别为直杆桁架式筏架和螺旋杆桁架式筏架的加速度振级落差。

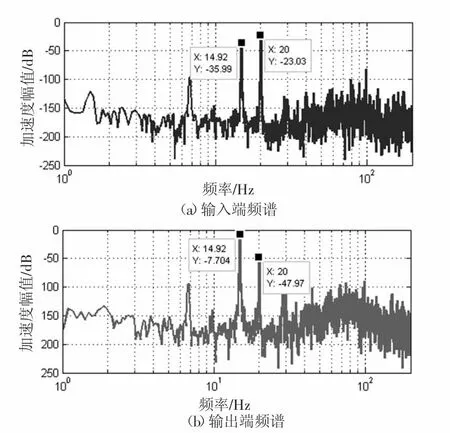
图16 电动机激励下直杆桁架式筏架频谱

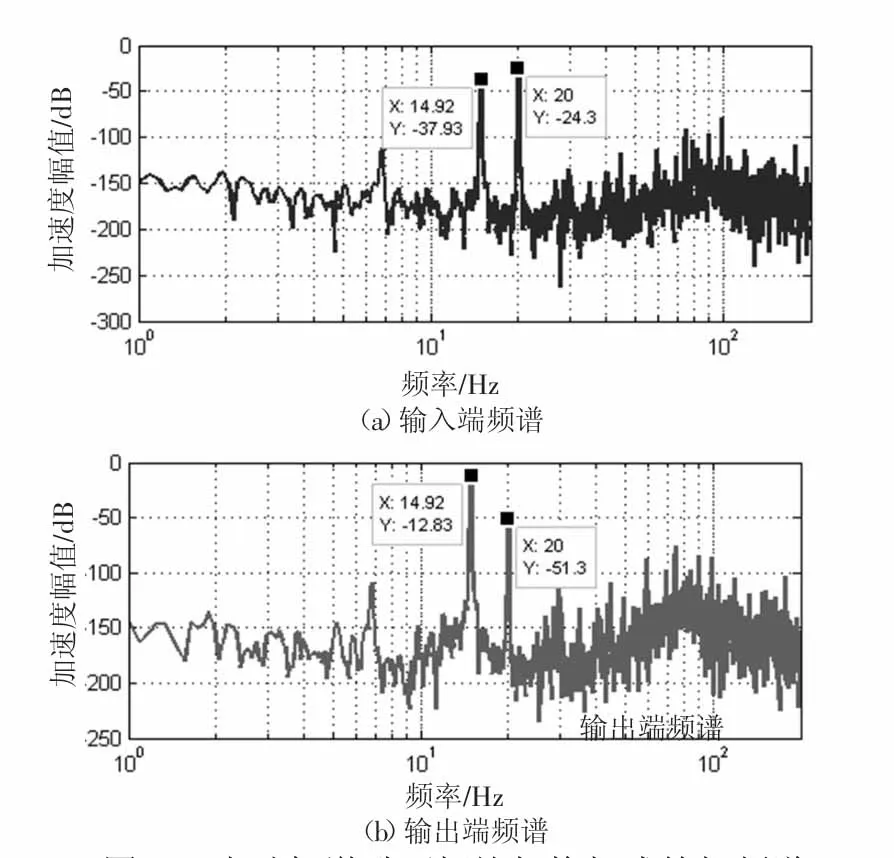
图17 电动机激励下螺旋杆桁架式筏架频谱

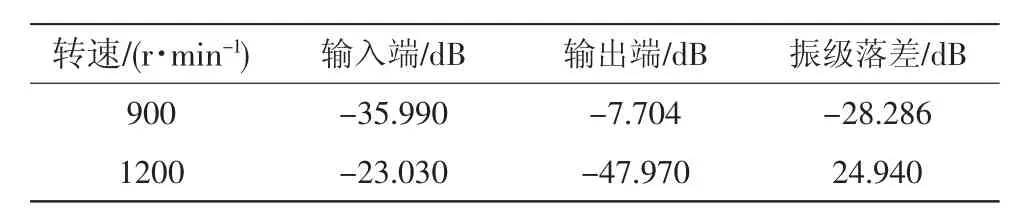
表1 直杆桁架式筏架加速度振级落差

表2 螺旋杆桁架式筏架加速度振级落差

通过表1和表2可知，无论在转速为900 r/min还是在转速为1200 r/min时，螺旋杆桁架式筏架的加速度振级落差都大于直杆桁架式筏架的加速度振级落差，即螺旋杆桁架式筏架的隔振性能较好。而且在转速为900 r/min即在频率为15 Hz时，两种筏架均出现振动放大现象，与扫频实验相一致。

5 结论

本文基于在相同材料中，振动传递路程越长，振动的能量损耗越多，隔振效果越好，提出了一种螺旋杆结构。针对一维螺旋杆桁架和二维螺旋杆桁架进行振动传递的分析，并与直杆桁架进行对比，得出了螺旋杆结构可以提升振动的抑制效果。最后设计了一种螺旋杆桁架式筏架，对其进行仿真分析和实验研究，结果表明，与一般的直杆桁架式筏架相比，螺旋杆桁架式筏架整体上可以更好地抑制振动传递，即具有更好的隔振性能。