似曾相识燕归来 数与形合“e”点通*——例谈浙江省数学高考向量题的解法策略

●李承法 (开化中学，浙江开化 324300)

一年一度的浙江省数学高考向量题八方关注，被广大高考试题研究者所青睐．笔者认为2018年浙江省数学高考第9题依然尽显“浙江风格”，题面简洁，题新意深．试题围绕单位向量、向量的核心考点来创新命题，精彩纷呈．历年浙江卷向量题的核心考点是模、数量积、线性运算．因命题的角度不同，每年都会有新颖的试题情境，特别是特殊向量——单位向量出现时，就有不同的试题和解法．笔者以这道题及近年来浙江卷涉及单位向量的高考试题为例，梳理高考向量题的考查视角和解题策略，并作变式思考．

1 e与模:借用单位向量|e|=1

向量模就是向量长度，涉及它的问题求解通常有几何和代数两个角度:线段长

例1已知a，b，e是平面向量，e是单位向量．若非零向量a与e的夹角为，向量 b满足 b2－4e·b+3=0，则|a －b|的最小值是 ( )

(2018年浙江省数学高考试题第9题)

解法1(几何角度)因为

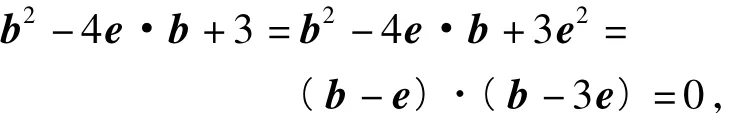
所以向量b的终点在以AE为直径的圆上(如图1)，于是|a－b|的最小值为|BC | =槡3－1．故选A．

评注解法1从分析问题的数量关系入手，借用单位向量e“数”的属性——长度为1，利用方程的相关知识，再运用向量a－b“形”的属性，由几何直观观察可知:当DC⊥OC时，|BC|最小．

图1

图2

解法2(代数角度)设单位向量e=(1，0)，向量 b=(x，y)，因为 b2－4e·b+3=0，所以

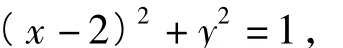
即从而向量b的终点B在以点D(2，0)为圆心、1为半径的圆上(如图2)．设a所在直线方程为l:y=槡3x，则|a－b|表示b的终点到直线l的距离．又圆心D到直线l的距离为

评注坐标法是解决向量问题的重要方法之一，其特点就是用代数的方法处理几何问题，思维起点低，易于操作．解法2用坐标法快速求解，不仅思维量小，运算量也不大，降低了思维起点．前提是合理建系，否则会人为增加运算量．

解法3(代数角度)因为b2－4e·b+3=0，所以

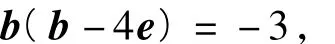
即

整理得

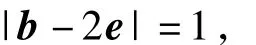
下同解法1，略．

评注本题的核心是对数量积e，b的处理．关于数量积的运算可用极化恒等式．解法3用极化恒等式聚焦本质，将几何与代数有机结合，巧妙转化数量积，快速得到向量b的轨迹，从而找到解决问题的突破口．

解法4(代数角度)由解法3知|b－2e|=1，由图1得

评注问题的“形”往往蕴含着解题的思路与方法．试题是向量模的最值问题，可以从绝对值的“形”入手，进行合理构造，寻求解题思路．解法4由“形”而思，合理构造．基于|a－b|及a，b的模构造三角不等式，充分利用了绝对值的“形”，这里a，b几何意义的确定是关键，同时结合圆的几何性质，解法4显得灵活快捷．

1．1 题源回溯

回溯浙江省数学高考单独命题以来，笔者认为例1与10年前这道高考题(例2)同源．

例2已知a，b是平面内两个互相垂直的单位向量．若向量c满足(a－c)(b－c)=0，则|c|的最大值是 ( )

分析如图30，所以点C在以AB为直径的圆上，故|c|=|OC|的最大值为圆的直径|AB|，即槡2．

图3

(2008年浙江省数学高考理科试题第9题)

此题为向量的模的最值问题，涉及了单位向量并应用了单位向量模为1的属性，形式上看是关于向量c的方程，本质是考查圆的向量式方程．因此说例1与例2是同源试题，只不过例1对单位向量的设置更加灵活，情景更为新颖、独到，令人拍案称绝．

1．2 例1的变式与简解

变式1己知 a=xb+yc(其中 x，y∈R)，|a|=|b|=2，c为单位向量，a·b－(a+b)c+1=0，则|a－b|的取值范围是______．

解法1(代数角度:模的平方)因为

所以要求|a－b|的取值范围，只需求a·b的取值范围．由a·b－(a+b)c+1=0得a·b+1=(a+b)c=|a+b|·|c|cos θ≤|a+b|，其中 θ= ＜a+b，c＞，从而

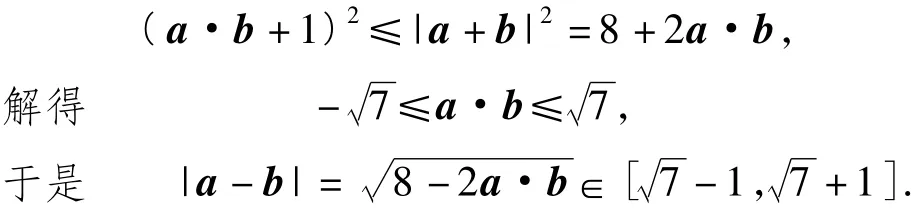
解法2(几何角度:构图建系)如图 4，设 c=(1，0)，A，B是以O为圆心、2为半径的圆上两点．由 a·b－(a+b)c+1=0得

图4

2 e与夹角:几何图形中善用e

除了以圆为背景外，含有向量的模和单位向量e的问题还常常以三角形、平行四边形、圆的弧、圆的弦(直径)等几何图形为背景．

例3己知平面向量 α，β(其中 α≠0，α≠β)，且满足|β|=1，α与 β －α的夹角为120°，则|α|的取值范围是______．

(2010年浙江省数学高考理科试题第16题)

解法1(几何角度)设(如图5)，则

图6

图5

根据α与β－α所成角为120°，知∠ACB=60°为定角，对边AB=|β|=1为定值．作△ABC的外接圆，则点C在(优弧)上运动，恒有∠ACB=60°，从而|α|的取值范围在圆中即为弦AC长度的变化范围，可直接找出临界位置(如图6)，得|α|∈

解法2(代数角度)

思路1作OACB(如图7)，则

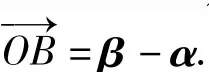
图7

由 题 意 知 ∠OBC=60°，在△OBC中，显然

思路2在△OBC 中，设|α|=x，|β － α|=t，由余弦定理得

即

接着用主元法(t为主元)得此方程(函数)有正根(零点)，对称轴

评注通过几何图形，借用正余弦定理，简化了计算过程．若是用两向量的夹角公式直接翻译条件“α与β－α的夹角为120°”，计算就显得繁琐了，解题目标不容易达成．

3 e与数量积:巧用数量积之投影形式

关于数量积的运算主要有3条路径，即定义法、投影法和公式法，因此涉及e的数量积试题根据情境条件可以选择不同的计算形式．

例4已知 e1，e2是平面单位向量，且 e1·，若平面向量 b满足 b·e=b·e=1，则12|b|= ______．

(2015年浙江省数学高考文科试题第13题)

分析(几何角度)由e1，e2是单位向量，且的夹角为 60°．又 b·e=b·1e2=1，从而b在e1，e2方向上的射影都为1，由图8可知△OAC≌△OBC(HL)，于是在△OAC中，

评注本题用几何法直观快速．解题的关键是对数量积几何意义的理解:向量b在e1，e2方向上的射影都为1．

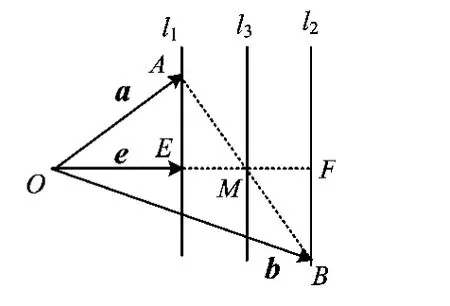
图9

图8

变式2已知平面向量 a，b，e，满足|e|=1，a·e=1，b·e=2，|a －b|=2，则 a·b的最小值为______．(2014年浙江省温州市高三第一次适应性测试数学理科试题第17题)

分析如图9，设 e，a，b是以 O为起点、分别以E，A，B为终点的向量．由向量数量积的几何意义知:点A在垂直于e的直线l1上，且点O到直线l1的距离为1;点B在垂直于e的直线l2上，且点O到直线l2的距离为2．由|a－b|=2知|AB|=2，设M为线段AB的中点，由极化恒等式得

因此求a·b的最小值即求|OM|的最小值．显然点M的轨迹为垂直于e的一条直线l3，而点O到直线l3的距离为，从而

评注平面向量数量积可以转化为数量积的几何意义或者极化恒等式来代数运算．

4 e与线性运算:再用e和数量积的意义

经典的试题经得起时间的洗礼，多年以后总会反复出现，只不过将e重新包装，旧曲换新词，十年后再出新题．如2005年浙江卷向量恒成立问题换成包含空间向量的基本定理，e换成二元线性运算xe1+ye2，就包装成了2015年浙江卷向量恒成立试题(例5)，这当然同样可用通性解法(代数法或几何法)来解决，只不过是将原来考查平面上点线距升级成考查空间的点面距(即点到平面的距离)问题，这可谓是“似曾相识燕归来，数与形合‘e’点通”．

图10

图11

如图11，因为∠OBD=∠OAD=90°，所以点O，A，D，B 共圆，OD 为圆的直径，从而

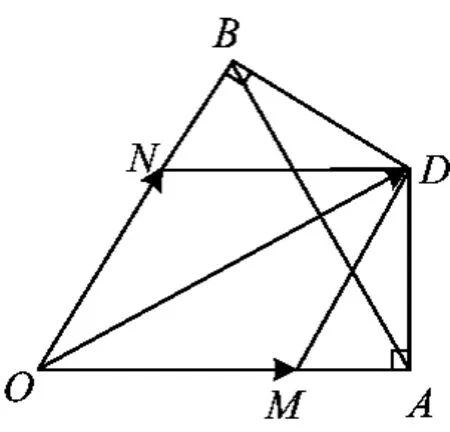
图12

于是

从而BH的长就是点B到平面OMN的距离．

评注本题以空间向量形式呈现常见的几何结论:平面外的点到平面的距离，垂线段最短．一般地，对于共起点的空间向量 a，b，c，|a+λb+μc|(其中λ∈R)表示向量a的终点与以不共线向量b，c所在平面上点的距离(点面距)，容易得到其最(其中n为向量b，c所在平面的法向量)．

5 e与不等式:善用重要不等式

例6已知向量 a，b，|a|=1，|b|=2，若对任意单位向量e，均有则 a·b的最大值是______．

(2016年浙江省数学高考理科试题第15题)

解法1(代数角度)由|(a+b)·e|≤|a·e|+|b·e|

评注本题用了两类重要不等式:

1)|a·e|=|acos＜ a，e ＞ |≤|a|，|b·e|=|bcos＜b，e ＞ |≤|b|;2)|a+b|≤|a|+|b|．

解法2(投影法)设向量a，b的夹角为θ，向量a，e的夹角为α，则可设向量b，e的夹角为θ+α，由向量数量积的几何意义得

解法3(几何角度)如图13，设，(a－b)2=2(a2+b2)=10．作 AA1⊥e 于点 A1，BB1⊥e于点B1，从而共线时，等号成立．若对任意单位向量e，均有

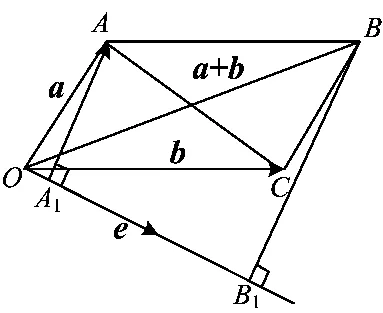
图13

当且仅当单位向量e与向量a+b共线时，等号成立［2］．

6 基于数学核心素养的高考向量复习启示

6．1 调整教学方法，优化教学内容

浙江省数学高考向量试题的考查内容与命题立意充分体现了基础性、综合性、应用性和创新性．因此，向量复习教学中教师要重视“四基”与数学素养的培养提升，做好课堂教学设计，应更多地关注数学的思维、数学的本质，而不要拘泥于对题型的研究、套路的演练，注重向量题的通性通法，注重向量的数形属性的运用教学．

6．2 向量题专项训练策略

每年高考向量问题的变，不论是单位向量e，还是其他向量，不管形式如何变化，我们只有以不变应万变．一是向量基础知识不会变:建议在第一轮复习时，重点放在基础知识的全面落实上，以夯实基础的不变应向量问题的万变;二是高考向量问题的命题思路和着力点不会变:在第二轮复习时，最好采取专项训练的方式，通过专题讲解和专题练习提高思维能力和解题水平，在向量解题教学中，重视发展学生在数学解题中的代数或几何处理能力，优化学生向量知识的认知结构，强化向量的“数”和“形”属性的理解和数学问题的理解，着重寻求问题的通解通法［3］，着重解题策略的选择，实现数形结合．