扎根数学课堂 培育核心素养*
2018-11-10义乌中学浙江义乌322000
●方 治 (义乌中学,浙江义乌 322000)
1 数学核心素养的提出是时代发展的新诉求
回顾高中数学课程目标的发展变化,呈现出几个重要的节点:1956年,《中学数学教学大纲》提出发展学生的“逻辑思维和空间想象能力”,1963年修补为发展学生“正确而且迅速的计算能力和逻辑推理能力”;1978年,《全日制中学数学教学大纲》扩充为“三大基本能力”,即运算、逻辑思维和空间想象能力;2003年,《普通高中数学课程标准(实验)》将“三大基本能力”扩充成了“五大基本能力”,即空间想象、抽象概括、推理论证、运算求解和数据处理能力;《普通高中数学课程标准(2017年)》(以下简称《新课标》)提出六大数学核心素养,体现了数学的本质特征,精准聚焦了数学的关键能力和思维品质,既是对历史的继承和发展,也是时代发展的新需要.纵观各个历史节点所提出的高中数学课程目标,它们的确定呈现出一定的稳定性、延续性和时代性,体现了从知识层面到能力层面再到素养层面的转型.
2 数学核心素养的要义需要教师深度地理解
数学核心素养是适应个人终身发展和社会发展需要的具有数学基本特征的思维品质与关键能力以及情感、态度与价值观的综合体现,是在数学学习和应用的过程中逐步形成和发展的.数学核心素养包括数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析,它们既相对独立、又相互交融,是一个有机的整体[1].
由“双基”内核发展而来的“四基”结构(基础知识、基本技能、基本思想、基本活动经验)为数学核心素养的发展夯实了学习基础.以前的“双基”侧重于对数学原理、定理、概念、公式等结论性知识的反映,但结论性知识的掌握并不是数学学习的全部.正如数学家莱布尼兹所说:数学的本质不在于它的结论,而在于它的思想方法[2].因此“四基”结构比“双基”内核更为科学、合理,不仅注重结果性知识和客观性事实的掌握,而且还关注学生在亲身经历数学活动过程中的个性体验和感悟.从数学角度发现、提出、分析和解决问题能力(简称“四能”)的培养有效支撑了数学核心素养的发展,对比2003年的《课程标准》,新增了“发现问题的能力”,这是《新课标》对学生质疑批判意识和创新能力培养的体现.会用数学眼光观察、数学思维思考、数学语言表达现实世界(简称“三会”)是数学核心素养内隐特征的外在表现形式,是数学核心素养作用于学生后的数学行为表征[3].因此高中数学教师在数学教学中不应仅仅停留在教给学生一些结论性的知识,更应该创设多样的有效情境,让学生在丰富的数学活动中积累经验、感悟思想、领会精神和深化认识.
3 数学核心素养的落地应扎根于课堂的土壤
课堂是学生学习数学的主阵地,核心素养的习得和练就需要根植于课堂,教师应借助恰当的教学情境或者适切的数学问题促使学生发现论证、对比统算,实现具体与抽象、数与形、非数学与数学的多样转化,让学生在准确把握数学本质的同时潜移默化地习得.
3.1 依靠情境和结构抽象生成数学抽象核心素养
数学抽象是数学的基本思想,反映了数学的本质特征.它是对某一类事物或现象共同本质属性的数与形的描述,并用数学符号予以表征.笔者认为数学抽象素养的培养可从具体情境和结构情境的抽象中习得.
1)情境抽象.
数学的抽象性使得部分学生对数学的学习失去信心,也较难产生浓厚的学习兴趣,而数学概念的形成过程就是数学抽象的过程,因此教师应该创设情境,调动学生的学习积极性,让学生在数学化的过程中抽象出数学概念,从而习得数学抽象核心素养.
笔者在进行反证法的教学时,借助反映反证法的具体生动的故事情境引出课题,通过分析故事的逻辑推理方法归纳出反证法的证明要领.这样的预设和引入既提高了学生学习数学的兴趣,又使学生发展了数学抽象核心素养.
故事情境死囚逃生:古代有一贤臣被奸臣坑害,判了死罪,皇上念他过去有功,用抽纸片的形式决定他的命运,一张写“活”字,一张写“死”字,抽到“活”字可赦免,而奸臣夕毒,命人在两张纸片上都写上“死”字.诡计被贤臣的朋友知道,告诉了贤臣,贤臣想了想,高兴地说:“我活了!”
抽象化成数学命题己知两张写着“死”字的纸片,某人抽取了一张.求证:某人“活”了.
证明假设某人“死”了.那么没有抽到的纸片一定写“活”字,可是因为两张都是“死”字,所以没有抽到的纸片一定是“死”字,因此二者矛盾.故某人“活”了.
处决前抽纸片开始了,只见贤臣抽出一张纸片谁也不让看就吞下了肚,监斩官只好看剩下的纸片,剩下的字无疑是个“死”字,于是贤臣被赦免了.
归纳反证法证明命题的一般步骤:①反设,作出与求证结论相反的假设;②归谬,将反设作为条件添加到题设中去,通过一系列正确的推理导出矛盾;③结论,肯定原命题成立.
2)结构抽象.
数学的抽象性很大程度上体现在数学抽象的符号上.学生感觉数学复杂主要是源于对数学符号和结构特征的理解,学生数学抽象素养的提升除了要在抽象的情境中培养外,也需要学生从分析和处理抽象的数学结构特征中去凝练.笔者从2015年全国数学高考新课标卷Ⅱ理科第12题出发进行变式题链的设计与研究,在引领学生分析不同抽象式的结构特征中提升学生的数学抽象核心素养.
例1设函数f'(x)是奇函数f(x)(其中x∈R)的导函数,f(-1)=0,当 x>0时,xf'(x)-f(x)<0,则使得f(x)>0成立的x的取值范围是( )
A.( -∞,-1)∪(0,1)
B.( -1,0)∪(1,+∞)
C.(-∞,-1)∪(-1,0)
D.(0,1)∪(1,+∞)
(2015年全国数学高考卷Ⅱ理科试题第12题)
变式1设函数f'(x)是奇函数f(x)(其中x∈R)的导函数,f( -1)=0,当 x>0时,xf'(x) -2f(x)<0,求使f(x)>0成立的x的取值范围.
变式2设函数f'(x)是奇函数f(x)(其中x∈R)的导函数,f( -1)=0,当 x>0时,xf'(x) -nf(x)<0,求使f(x)>0成立的x的取值范围.
变式3设函数f'(x)是奇函数f(x)(其中x∈R)的导函数,f( -1)=0,当 x>0 时,xf'(x)+f(x)<0,求使f(x)>0成立的x的取值范围.
变式4设函数f'(x)是奇函数f(x)(其中x∈R)的导函数,f( -1)=0,当 x>0 时,xf'(x)+2f(x)<0,求使f(x)>0成立的x的取值范围.
变式5设函数f'(x)是奇函数f(x)(其中x∈R)的导函数,f( -1)=0,当 x>0 时,xf'(x)+nf(x)<0,求使f(x)>0成立的x的取值范围.
变式6设函数f'(x)是奇函数f(x)(其中x∈R)的导函数,f'(x)-f(x)<0,求使 f(x)>0成立的x的取值范围.
变式7设函数f'(x)是奇函数f(x)(其中x∈R)的导函数,f'(x)-2f(x)<0,求使 f(x)>0成立的x的取值范围.
变式8设函数f'(x)是奇函数f(x)(其中x∈R)的导函数,f'(x)-nf(x)<0,求使 f(x)>0成立的x的取值范围.
变式9设函数f'(x)是奇函数f(x)(其中x∈R)的导函数,f'(x)+f(x)<0,求使 f(x)>0成立的x的取值范围.
变式10设函数f'(x)是奇函数f(x)(其中x∈R)的导函数,f'(x)+2f(x)<0,求使 f(x)>0成立的x的取值范围.
变式11设函数f'(x)是奇函数f(x)(其中x∈R)的导函数,f'(x)+nf(x)<0,求使 f(x)>0成立的x的取值范围.
3.2 通过数化和求模过程生成数学建模核心素养
数学建模是对现实问题进行数化处理和表达,然后用所学的数学知识与方法解决问题的过程.教师要善于挖掘生活中有价值的数学问题,让学生亲历数化和求模的过程.结合当下高考的选考现实,笔者设计了如下的现实问题,由于这个问题与学生的相关度很高,因此能迅速激起学生的研究兴趣,学生在解决问题的过程中提升了自身的数学建模核心素养.
例2(现实问题)已知某校选考物理和技术的学生各有若干人.若选考物理的学生中有90人改选技术,则选考技术的学生是选考物理学生的两倍;若选考技术的学生有部分改选物理,则选考物理的总人数是选考技术的6倍,求选考物理的学生原来最少有几人?
解假设原来选考物理和技术的学生各有x,y人,由已知条件可知

再设选考技术的学生有z人改选物理,则
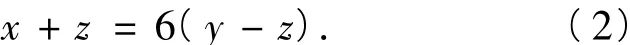
由式(1)和式(2)消去y,可得
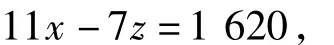
由于x,z都是正整数,因此

故
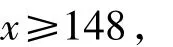
3.3 依托概率统计问题生成数据分析核心素养
数据分析是指针对研究对象获得相关数据,运用统计的思维和方法对数据中的有用信息进行分析和推断然后形成知识的过程.在当下的大数据时代,数据的采集、处理和统计分析的意识和能力至关重要.下面问题的设计意在让学生运用数据分析的方法解决抽样、概率、分布列和期望等概率统计问题,它可以培养学生的数据分析意识和数据处理能力,养成用数据思考问题的习惯,进而提升数据分析核心素养.
例3(概率统计)走班制教学是顺应新时代发展和高考新方案要求的一项重要举措.某校在高二年级实行选课走班教学,学校在同一上课时段为学生提供物、化、生、政、史、地、技7种课程,每个学生从7门课程中选择一门学习,该校高二年级900名学生的选课人数统计如表1所示:

表1 7门课程的选课人数统计
1)根据表1中的数据,写出a,b的值.
2)为了了解学生选课走班的情况,用分层抽样的方法从这900名学生中抽取20人进行座谈反馈.
①从选出的20名学生中随机抽取3人发言,求这3人中至少有2人选择技术的概率;
②从选出的20名学生中随机抽取3人发言,记这3人中选择物理的人数为X,选择政治的人数为Y,设随机变量ξ=X-Y,求随机变量ξ的分布列和数学期望E(ξ).
解1)a=10%,b=135.
2)抽取的20人中选择物理的人数应为20×15%=3,选择化学的人数应为20×20%=4,选择生物的人数应为20×10%=2,选择政治的人数应为20×10%=2,选择历史的人数应为20×15%=3,选择地理的人数应为20×10%=2,选择技术的人数应为20×20%=4.
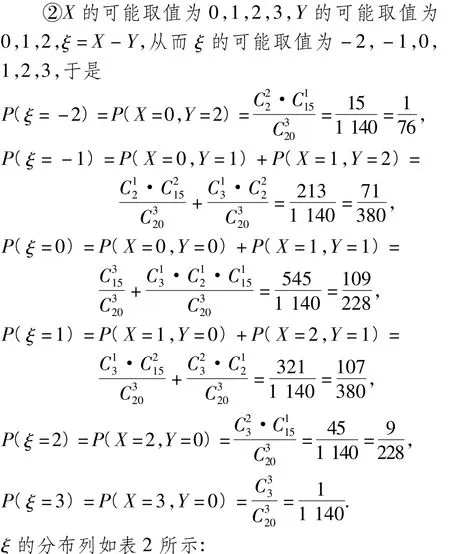
表2 的分布列
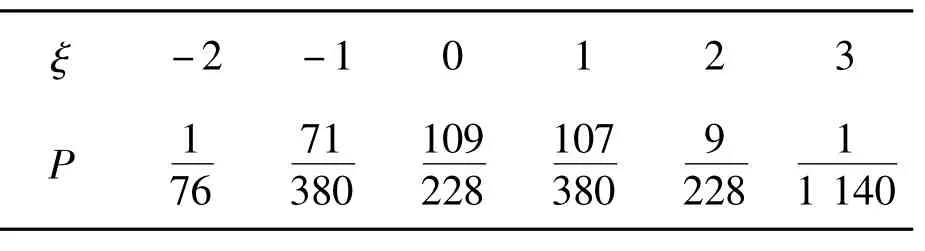
表2 的分布列
ξ -2 -1 0 1 2 3 P 17110910791 763802283802281140

3.4 借助数化形和形转型生成直观想象核心素养
直观想象是指借助几何直观和空间想象感知事物的形态与变化,利用图形理解和解决数学问题的过程.几何直观是通过图形生动形象地反映和刻画数学问题,它可以将某些复杂的数学问题简单化,实现抽象向直观转换.空间想象集中体现在由空间图形出发,凭借空间想象能力去想象空间模型,利用模型的特征解决数学问题.
1)数化形.
某些数学式子从结构特征上分析和还原,发现具有明显的几何特征,我们可以用图形直观反映式子背后的几何意义,让抽象式子几何直观化,在快速解决问题的同时培养学生的直观想象核心素养.
例4(最值问题)设 x,y∈R+,求函数 f(x,的最小值.
解根号里的式子结构如图1所示.设AP=x,AQ=y,∠BAP=30°,∠PAQ=60°,∠QAC=30°,则由三角形的余弦定理可知
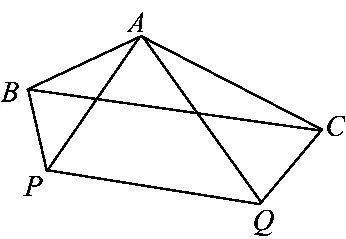
图1

2)形转型.
空间想象是人们对客观事物的空间形式进行观察、分析和认知的抽象思维能力.立体几何问题可有效承载学生直观想象能力的培养,发挥学生的空间想象能力,把图形与模型有效对接,在借助模型特性解决问题的过程中培育学生的直观想象核心素养.
例5(立体几何问题)如图2,在棱长为a的正四面体ABCD中,G为△BCD的重心,M为线段AG的中点,求三棱锥M-BCD的外接球和内切球半径之比.
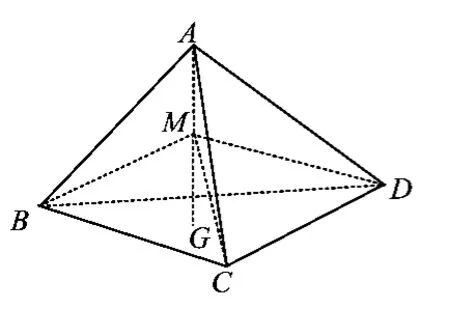
图2

图3
解由于正四面体ABCD的棱长为a,G为△BCD的重心,M为线段AG的中点,因此根据空间几何图形的对称性可知MB=MC=MD,而且
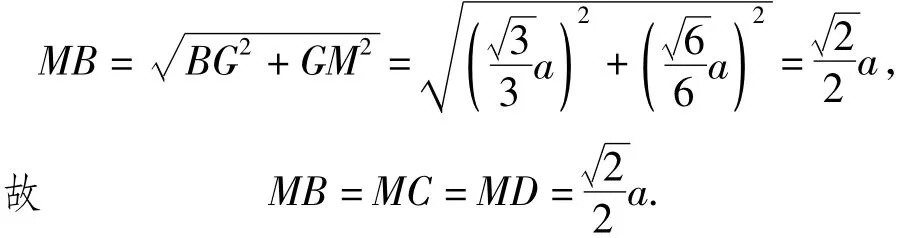
而BC=CD=DB=a,于是 MC,MB,MD 两两垂直,三棱锥M-BCD的外接球直径等于以MC,MB,MD为棱的正方体的体对角线,故三棱锥M-BCD的外接球半径为
假设三棱锥M-BCD的内切球半径为r,则根据球和三棱锥M-BCD的对称性作出一个特殊的截面(如图3所示),其中内切球的球心为O,CD的中点为 E,内切球切面 MCD于点 F.由△MOF∽△MGE可知

3.5 亲历发现和论证过程生成逻辑推理核心素养
逻辑推理是指从一些事实和命题出发,依据逻辑规则推出一个命题的思维过程.它包括合情推理和演绎推理,正如波利亚所说:“数学具有两个面——以欧几里得方式表现出来的数学看上去是一种系统的演绎科学;但在形成过程中的数学看上去却是一种实验性的归纳科学.”[4]在高中数学课堂教学中,教师应创设问题情境,让学生在亲历发现和论证过程中练就逻辑推理核心素养.
求复杂递推数列的通项公式问题就是培养学生逻辑推理素养的良好载体.笔者在上已知数列的递推公式求通项公式时,设计了如下问题,让学生亲历发现和论证的过程.

解由 a1=5,a2=13其中 n≥2)可知 a3=29,a4=61,猜想 an=2n+2-3.
下面用数学归纳法证明an=2n+2-3对一切正整数都成立:

因此当n=k+2时等式也成立,故猜想an=2n+2-3对一切正整数都成立.
3.6 基于同类异算生成数学运算核心素养
数学运算是指在明晰运算对象的基础上,依据运算法则解决数学问题的过程.对于同类问题,基于不同算理展开的不同算法的比较分析可以让学生明晰不同算法的同时掌握最优算法,从而驱动学生生成数学运算核心素养.
曲线上存在两点关于某动直线对称的问题是一类综合性较强的问题.解决此类问题可以联立方程组利用韦达定理或点差法加以解决,对于直线、圆、椭圆、双曲线及抛物线等不同曲线,分析特殊曲线算法的特殊性以及一般曲线不同算法的优劣性,让学生明晰这类问题减少计算量的方法,提升学生的运算能力.

解1)若y=2x-1上存在上两点 A(x1,y1),B(x,y)关于直线 y=kx+对称,则两直线只能

22相互垂直,故k的值为-


