基于核心内容的试题命制*——以一道导数原创题的命制过程为例

●张 玮 胡 满 (学军中学，浙江 杭州 310012)

0 引言

2018年3月，笔者在参与A校高三年级的一次考试命题时，需要提供一道有关导数的试题．笔者认为命制的试题应侧重于考查该学科的主干知识，考查主干知识应侧重于考查其中的核心内容．在高中阶段，以导数的计算、求函数的单调区间作为导数内容的重中之重，而求函数的最大值、最小值、用导数证明不等式、求曲线的切线等内容，都是在求得函数的导数或单调区间之后的一些衍生产物．

2017年是浙江省高考改革后，文理不分科的第一年高考．这一年的高考导数题，主要考查了求函数的导数、求函数的单调区间和值域的问题．虽然2017年浙江省数学高考试题的总体难度明显下降，但是对学生数学能力的考查没有下降．就导数这一块内容而言，2017年的试题对于导数核心内容的考查丝毫没有减少，反而用一种更加直接的方式呈现了出来．因此，笔者认为在新高考的背景下，试题应突出用导数求单调区间这部分内容．经过反复研磨，最终给出了一道由笔者独立编拟的导数原创题(例1)．该题主要考查导数的计算和求函数的单调区间，在此基础之上，进而考查函数最小值的问题．

例1设f(x)=x－ln(ax+a+1)+1．

1)若a=1，求f(x)的单调区间;

2)若对于任意x≥－1，不等式f(x)≥0恒成立，求a的最大值．

综上可知，a的最大值为1．

1 编题的背景

导数是高等数学的基础内容，可以用它来刻画函数的凹凸性，该性质是函数的一个很重要的性质，它可以通过二阶导数的符号来确定．在高中阶段，导数只是用来求函数单调区间的一个有力工具，而求函数单调区间的重要性在于求函数的最值(极值是局部的最值)．在已知最值之后，很多问题才能展开，比如证明不等式等问题．在有关导数的试题中，指数函数f(x)=ex是“常客”，而且它在(0，1)处的切线为 y=x+1，并且当 x≥0时，满足ex≥x+1．这个不等式非常重要，不仅是因为它蕴含了曲线和切线的位置关系，而且它还可以通过适当的代换，得到很多有用的结论．如:

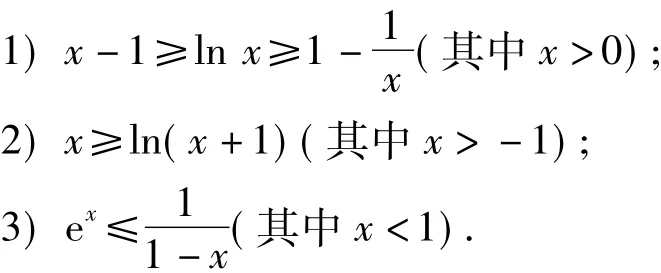
这些不等式的应用活跃在各种考试当中，比如:

例2已知数列{xn}，满足x1=1，xn=xn+1+ln(xn+1+1)(其中 n∈N)，证明:当 n∈N*时，

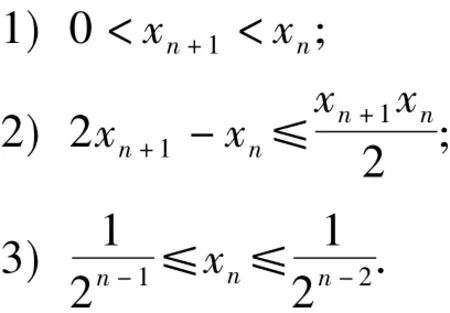
(2017年浙江省数学高考试题第22题)

1)略．

2)分析原命题等价于，即证明

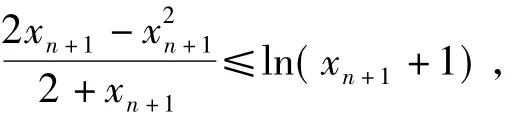
利用结论1)的右边不等式，即得．

3)分析利用结论2)，放缩后可得

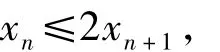
即

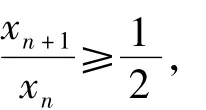
因此左边的不等式得证(右边证明略)．

从中可以看出高考试题对此类不等式也青睐有加．此外在高等数学中，函数f(x)=ex在x=0处的泰勒展开式为

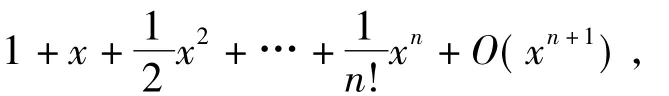
因此不等式ex≥x+1还具有一定的高等数学背景．在高中阶段，由于教材对函数的二阶导数要求不高以及高考导数试题的难度下降等原因，没有选择不等式．但是对于不等式ex≥x+1，笔者希望它能动起来，故考虑再加个参数．不等式ex≥x+a显然过于简单，从而考虑ex≥ax+1;再由y=x+1和f(x)=ex的位置关系可知，a≤1，于是原创题(例1)的函数模型f(x)=ex－ax－1就此确定．之后笔者在2012年湖南省数学高考理科试题中发现了它的踪迹:

例3已知函数f(x)=eax－x(其中a≠0)．

1)对任意x∈R，f(x)≥1恒成立，求实数a的取值集合;

2)略．

(2012年湖南省数学高考理科试题第22题)

分析令t=ax，则 eax－x≥1，从而

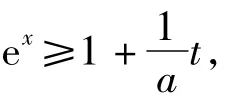
由此原不等式转化为不等式ex≥1+ax的形式．

模型确定之后，接下来的问题就是考什么?由于导数部分的核心内容是导数的计算和函数的单调区间，因此命题方向不能偏．笔者设想:第1)小题可以求单调区间;第2)小题可以设置一些已知条件，然后求参数a的范围或最大值．大方向基本确定了，那么在导数的计算中如何考查?大多数函数的求导中都会包含四则运算，而复合函数的求导过程中，必定包含了基本初等函数的求导公式．因此笔者的想法是:先构造一个函数，得到试题的雏形;然后再通过适当的改造使得函数结构符合考查要求．

2 编题的过程

笔者希望通过求导之后得到一个可以因式分解的式子，方便学生得到该函数的单调区间，从而降低第1)小题的难度．得到试题的第1稿为:

第1稿已知函数f(x)=ex(1+ax+x2)．

1)若a=1，求f(x)的单调区间;

由于第2)小题形式不够美观，笔者对此不太满意，因此想到对不等式作变形，便有了第2稿:

第2稿已知函数f(x)=ex(1+ax+x2)．

1)若a=1，求f(x)的单调区间;

这一稿虽然形式上比第1稿漂亮了点，但是ex出现了两次，且函数f(x)中也有因子ex，感觉过于累赘，且拼凑的痕迹也太过明显．笔者意识到:若不改变函数的结构，上述两稿的问题解决起来相对比较困难，那么该选用什么函数呢?因为最后都归结到不等式ex≥ax+1，所以可以通过对x进行赋值来改变函数的结构．从第2稿不等式的形式，笔者得到了启发，便有了第3稿:

第3稿已知函数f(x)alnx．

1)若a=1，求f(x)的单调区间;

2)若对于任意x＞0，不等式f(x)≥0恒成立，求a的最大值．

第3稿虽然解决了之前两稿的问题，但是函数较为复杂．特别是第1)小题，学生能否求出单调区间，这成为笔者心头的又一担心．经过求导发现

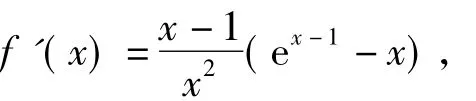
利用ex－1≥x这个结论，第1)小题不难求出．但是对于第2)小题，如果按照笔者的思路去求解，则需要利用等式将问题进行转化，而这是个难点，学生很难想到．回顾平时的课堂教学，要解决第2)小题，学生应该还有两种方法:

方法1进行参变量分离．原不等式化为

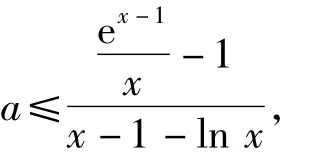
然后再求当x＞0时，不等式右边式子的最小值．

对学生而言这显然很困难，故此路不通．

方法2直接求原函数的最小值，只需要最小值非负即可．经过求导，得

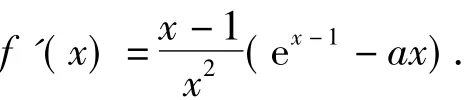
因单调区间不容易求出，故此路不通．由此看来，要解决第2)小题似乎只有“华山一条路”，即只能沿着笔者的设计思路去求解．

若此题作为“老高考”的压轴题，也许还合适;若作为“新高考”的试题，显然也不合时宜，入口太窄，难度太大．一个好的试题，应该有多个入口供学生选择，可以通过不同的角度来诠释．因此，笔者决定继续改．考虑对第3稿的函数作代换，于是决定将x换成x+1，得到函数

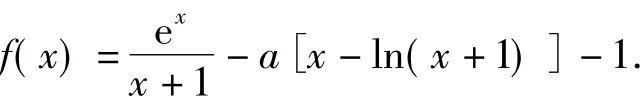
1)求f(x)的单调区间;

2)若不等式f(x)≥1+alnf(x)恒成立，求a的最大值．

第4稿的题干显然更简洁，只是第2)小题中，很容易联想到换元，会使得大部分学生的解法都一样，笔者对此不满意，故继续修改．由于第3稿是用不等式x－1－lnx≥0对x进行赋值，才使得函数变得复杂，因此想要让解析式更简单，就只能简化赋值的式子．笔者采用了第4稿的赋值方式，再对两边取对数，这样就得到了试题(即例1)．

3 试题的另解

在试题的命制过程中，笔者获得了第2)小题的其他两种解法．

解法2当a≤0时，显然符合，故只需考虑a＞0的情形．令 g(x)=ex－ax－1，则

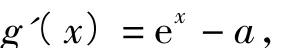
即函数g(x)在(lna，+∞)上单调递增，在(－∞，lna)上单调递减．

若a≤1，则 g(x)≥g(0)=0;若 a ＞1，则g(x)≥g(lna)=a－alna－1，因为 ln1＜1－1，aa所以g(lna)＜0．

因此，a的最大值为1．

解法3考虑参数分离:经检验a=1符合条件，即a的最大值为1．

4 考后的反馈

考后笔者参与了本次考试的阅卷，得到如下数据:本题满分15分，平均得分10．6分;40%左右的学生，得分不小于14分;10%左右的学生第1)小题求导数错误;还有30%左右的学生在做第2)小题时，出现了困难，得分很低，但是都猜出了答案．从得分情况来看，本题的区分度还可以．大部分学生对于高考要求的复合函数求导、求函数的单调区间问题掌握得很好，少部分学生还需要加强导数计算的训练．本题第2)小题，可以通过使［－1，+∞)上的最小值非负得到参数a的最大值．从得分情况来看，求函数在给定区间上的值域问题，还需要加强训练．第2)小题的解答，部分学生使用了解法3，参数分离之后，部分学生使用了高等数学中的洛必达法则，还有部分学生继续用导数求式子最小值．另外从学生的解答中，笔者发现了两种新解法如下:

解法4由第1)小题可知，当a=1时，

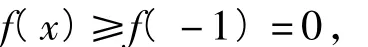
矛盾．

综上可得:a的最大值为1．

解法5当a=0时，f(x)=x+1，显然符合，故a的最大值非负．因为f(－1)=0，故存在δ∈( －1，0)，使得在( －1，δ)内，函数 f(x)单调递增，即导函数f'(x)在(－1，δ)内恒非负．又

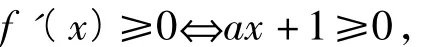
5 考后的反思

从考生答题的情况来看，大部分学生并没有被不等式x－1≥lnx卡住，反而给出了更漂亮的解法．从学生的整体答题情况来看，本文中提到的5种解法都有学生用到，解法的多样性是笔者在命题时所没有料到的．本题入口宽，解法多样，由此来看，应该是一个好的训练题．从第2)小题的答题情况来看，错误百出，这反映出部分学生的基本功不够踏实．2017年的浙江省数学高考导数试题突出导数计算和函数单调区间的考查，因此，在高三临考阶段，对于基础薄弱的学生，应该要更加重视核心内容的训练和讲解，做到有的放矢．

再次翻看学生的解答，笔者发现有少数学生因为没有处理好不等式，导致第 2)小题没有拿到高分，主要原因是不熟悉x－1－lnx≥0．因此若将第1)小题改为“当a=1时，令g(x)=f(x－2)，求g(x)的单调区间和最小值”可能会更好一点．考完后，笔者又重新翻看了2017年浙江省数学高考导数试题，函数中没有参数，不需要讨论，干干净净地考函数．因此，笔者认为:若把例1当作是一般的训练题，比较适合;若当作是高考模拟题，则不太适合．这也启示笔者:在编拟试题时，应尽可能地与高考试题接轨，让高三的师生明确方向．