基于动态数据驱动的反潜战仿真系统目标探测设计

张 翔, 李 革, 王 鹏

(国防科技大学系统工程学院, 湖南 长沙 410073)

0 引 言

反潜战仿真系统通过对目标潜艇建模分析,对其行为状态进行预测,为反潜武器装备研制、反潜作战能力评估、反潜战术战法研究提供支撑。目前大部分反潜战仿真模型在仿真开始时使用固定的参数配置,造成仿真系统不能够捕捉瞬时的变化,不能够对潜艇探测过程中发生的实时情况做出反应。动态数据驱动应用系统(dynamic data driven application system,DDDAS)是一种新机制,它允许在线测量数据动态同化进入正在运行的仿真模型中,同时正在运行的仿真模型也能反过来控制测量过程[1]。将动态数据驱动运用于反潜战仿真系统中,实时融合舰艇真实测量数据进入正在运行的仿真模型中,减轻模型表示或描述的不准确性,弥补模型的不完备性,从而改善模型,更加准确地预测目标潜艇的行为状态。反之,利用仿真对潜艇状态精确的预测来动态控制传感器实际的测量行为,改进收集数据的质量,获得高效准确的测量结果。

1 反潜战DDDAS闭环回路

1.1 原理描述

数据同化是DDDAS的实现基础,它能够把实时测量数据和仿真状态融合起来,决定真实系统的状态[2]。合理的数据同化算法能够极大地提高仿真模型的准确性和可信性。测量控制方法是根据仿真结果控制声呐传感器行为的具体方式,传感器要求反潜舰针对敌方潜艇进行机动,以便确保对距离的准确估计和可观测性[3]。为了保证舰艇的机动路径有利于声呐传感器对目标的探测,采用测量控制算法规划舰艇的机动路径。实时测量的数据被同化进入反潜战仿真模型中,仿真系统、测量系统和反潜战系统形成一个闭环控制回路。如图1所示,反潜战DDDAS有“一大两小”的闭合回路,分别实现不同的功能。在DDDAS的大回路中,反潜战真实系统产生的测量数据传递到基于随机有限集(random fonite set，RFS)的数据同化模块,然后同化后的数据作为基于RFS潜艇模型的输入,仿真模型预测潜艇的状态,反潜舰上的测量控制执行器根据目标潜艇状态产生控制动作,完成对反潜舰测量传感器的控制。两个小回路是“状态更新回路”和“动作控制回路”。其中“状态更新回路”的作用是对潜艇仿真模型状态的更新,基于RFS的测量仿真模型根据潜艇模型预测的潜艇状态,产生预测测量数据,再经过数据同化过程更新潜艇模型的仿真状态。“动作控制回路”通过基于RFS的测量控制系统生成控制参数,反潜舰测量传感器根据控制参数进行调整测量角度等相应测量动作。

图1 反潜战DDDAS的闭环回路Fig.1 Anti-submarine DDDAS closed loop

1.2 模型及数据描述

当模型明显是由一个或多个随机变量所决定,并且这些变量分别表示不确定的过程时,这个模型就是随机的[4]。有限集统计学提供了RFS的数学表示和操作,用RFS来建模潜艇状态和测量数据能使仿真的状态空间模型更加通用化,符合潜艇探测过程中的随机性和不确定性。基于RFS的测量模型和仿真模型能同时传递潜艇的数据和状态的估计,并且允许描述潜艇状态的构成向量是随机的、不同的和无序的。反潜战DDDAS的数据同化算法采用序贯蒙特卡罗(SMC)的方法实现,SMC是一种粒子滤波算法。传统的基于SMC的数据同化算法是以向量的形式表示数据,随机向量的数据同化算法要求每个向量的维数和元素的顺序事先制定并且保持一致。这种测量数据的数据表示方法不能体现潜艇状态的随机性,也不能同时估计潜艇的数目和每个潜艇的状态。考虑到实际测量过程的诸多影响,必须采用恰当的数据描述,使注入潜艇仿真模型的同化测量数据更加准确真实,尽可能的避免由潜艇数量、错误测量、潜艇规避动作等因素导致测量数据的不确定性。

反潜过程中,潜艇出入战场探测区域是随机的,并且噪音等杂波的影响增加了潜艇存在的不确定性。为使目标潜艇的仿真模型更加准确和完善,使用状态空间模型结合随机有限集来构建潜艇仿真模型可以较好地描述目标潜艇存在的随机性和不确定性。数据同化把模型参数和状态当作随机变量,估计的不是一个具体的数值而是每一个变量的状态函数,从而仿真模型是用随机变量和概率密度函数构建的概率模型。一个随机有限集Z={z1,z2,…,zn}可以理解成有限集变量,它可以被建模成离散概率分布ρ(n)=Pr{|Z|=n}和一个对称的联合概率密度fn(z1,z2,…,zn)[5]。

状态空间模型演化方程为

Xk=fk|k-1(Xk-1)+vk

(1)

式中,fk|k-1表示演化方程的确定性部分,并且负责把状态映射到下一个时戳。v是状态演化的随机部分,它使得数据同化变得很必要。为了给出潜艇在战场的存在性和状态的统一的描述,用伯努利随机有限集建模潜艇的状态并描述潜艇状态的动态演化。

反潜舰上的测量系统探测到敌方潜艇是一个概率事件,所以有时不能探测到潜艇而生成测量数据。但是在随机有限集框架下构建通用测量模型是可实现的,测量数据中的探测不确定性和杂波通过Bernoulli随机有限集和Poisson随机有限集的叠加来描述[6]。测量系统产生的测量数据可以建模成随机有限集Z={z1,z2,…,zm},它的优势主要是测量的数目m=|Z|和构成向量z∈Z在测量空间Z⊆Rnz中是随机的,并且对测量数据的顺序不做假设要求。测量数据集Z的测量模型的数学形式为φ(Z|X),其中X是仿真状态的Bernoulli随机有限集。

2 基于RFS的数据同化算法

数据同化算法作为数据同化的重要组成部分,是连接观测数据与模型模拟预测的关键核心部分[7]。在反潜战DDDAS中,重点是把在线测量数据同化进正在运行的仿真模型中,实现这个过程有两个关键点:一是将数据同化过程等同为概率论中的贝叶斯推理,并基于RFS的方式实现;二是以序贯蒙特卡罗粒子滤波(SMC)的方法近似求解状态方程。

2.1 基于RFS的贝叶斯推理

数据同化是通过仿真模型和测量模型等先验分布推导出后验分布,进而更新仿真状态,从概率论的角度,可以看成是一个贝叶斯推理过程。贝叶斯理论能够建立不确定性环境的信任函数,并随时间推演这些函数。贝叶斯推理实质是用系统状态转移模型预测状态的先验概率密度,再使用最近的观测值进行修正,得到状态的后验概率密度。递推过程可以分为预测和更新两个步骤。

利用基于RFS的仿真模型和实际的测量数据,k时刻的后验有限集统计学密度用潜艇存在的后验概率和空间的后验概率描述。

潜艇存在的后验概率为

qk|k=p{|Xk|=1|Z1:k}

(2)

Xk={x}时潜艇的后验空间概率为

sk|k(xk)=p(xk|Z1:k)

(3)

数据同化过程需要同时传递式(2)～式(3)的两个变量。记k-1 时刻仿真状态的后验概率为fk-1|k-1(Xk-1|Z1:k-1)。基于随机有限集的预测方程为

fk|k-1(Xk|Z1:k-1)=

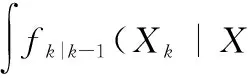
(4)

fk|k-1(Xk|Z1:k-1)=fk|k-1(Xk|∅)fk-1|k-1(∅|Z1:k-1)+

(5)

k-1时刻的后验概率密度函数是(qk-1|k-1,sk-1|k-1(x)),则从式(5)可以推导出预测方程为

qk|k-1=pb·(1-qk-1|k-1)+ps·qk-1|k-1

(6)

(7)

在贝叶斯理论中,更新的有限集统计学概率密度函数可以用如下方程计算，即

(8)

给定测量模型和预测方程式(6)和式(7),更新方程可以从式(8)推导得出

·qk|k-1

(9)

(10)

2.2 SMC近似求解

(11)

式中,δc(x)是狄克拉函数。预测的潜艇存在概率qk|k-1可以通过式(6)计算得到。根据式(7),预测的概率密度函数需要两项的和。从而sk|k-1(x)可以通过如下的粒子系统近似为

(12)

粒子从两个重要性密度中采样得到ρk和βk[8]，即

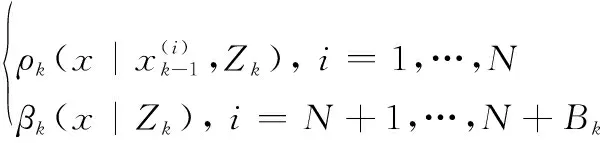
(13)

权重

(14)

式中,Bk是新生的粒子数目。

重要性函数ρk(x|xk-1,Zk)最简单的确定方法就是使用πk|k-1(xk|xk-1)。如果事先没有敌方潜艇行动计划的先验知识,假设它可能在状态空间S(X)中的任意位置出现,使用均匀分布来建模bk|k-1(x)。式(13)中的重要性密度βk同样需要支持bk|k-1(x)。

(15)

然后依据式(11),δk近似计算为

(16)

潜艇存在概率的更新依据式(9)来实现,对应的权重通过式(10)来实现，即

(17)

将权重进行归一化处理,得到归一化后的权重为

,i=1,…,N+Bk

(18)

3 基于RFS的测量控制方法

传感器相对于测量目标距离和角度影响着测量数据的精确性,测量数据的有效性和精确性对于数据同化过程十分重要,有效和精确的测量数据使潜艇的预测状态和更新状态更加精确,从而间接地提高仿真系统的精确度。在反潜战的DDDAS系统中,测量空间和状态空间是确定的,传感器的测量控制动作决定了获取的测量数据的精确性,最优的测量控制动作能保证测量系统的效率最大化并且向数据同化过程提供的测量数据更精确。在此,以传感器得到回报最多的有效测量数据作为评判测量动作的标准,建立回报函数模型。信息论中,测量数据即为获取的信息,回报函数作为每一个控制动作带来的信息增益的评价标准,后延概率密度函数用于表示不确定性的状态。

3.1 回报函数

通过基于RFS的贝叶斯推理得到了潜艇的状态预测和更新方程,但无法解析求解。为了建立对信息增益的描述,采用Rényi发散度作为回报函数。Rényi发散度用来度量两个概率密度不相似度的程度。反潜战仿真系统中,潜艇的状态具备马尔可夫链属性,即潜艇的下一状态仅与当前状态有关,与历史状态无关。所以,当前状态的概率密度与历史状态概率密度不相似程度越大,即Rényi发散度越大,信息增益就越大,相应的测量控制动作就越好。Rényi发散度定义为

(19)

式中,α(α≥0)表示对概率分布尾部的重视程度。

令uk表示在tk时刻能够使测量系统在tk+1时刻接收到测量数据而选择的控制动作,Uk表示在tk时刻可以采用的控制动作的集合,则有uk∈Uk。在tk时刻,不同的控制动作在tk+1时刻产生不同的预测测量数据集合Zk+1,而因为不同测量数据经同化后形成的仿真模型不同,所以潜艇仿真模型fk+1|k和测量仿真模型φk+1都取决于控制动作uk的选择。

如式(20),最优的控制动作是在每个仿真状态中最大化Rényi信息发散度的控制动作,它的确定需要考虑预测概率密度函数p和预测测量集合Z。

(20)

式中,φ(v,p,Z)是和控制动作v对应的实值回报函数。预测测量集合支持回报函数φ的计算。预测测量集合是假设控制动作已经执行之后获得的预测数据的集合,会产生不确定性。为了克服这种不确定性的影响,在式(20)中引入期望。式(20)中的回报函数是Rényi发散度为

依据uk产生预测概率密度函数为

fk+1|k(Xk+1|Z1:k,u0:k)=

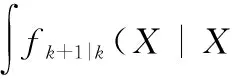
(21)

依据预测测量集合Zk+1的后验密度fk+1|k+1(Xk+1|Z1:k+1,u0:k)由式(8)写为

fk+1|k+1(Xk+1|Z1:k+1,u0:k)=

(22)

省略φ中的p和Z两个参数。依据式(19),回报函数φ可以表示为

(23)

在式(23)中A=fk+1|k+1(Xk+1|Z1:k+1,u0:k),B=fk+1|k(Xk+1|Z1:k,u0:k)。

3.2 回报函数的计算

由于数据同化过程和更新过程中的概率密度函数是伯努利有限集统计学概率密度函数,令式(23)中的fk+1|k(Xk+1|Z1:k,u0:k)和fk+1|k+1(Xk+1|Z1:k+1,u0:k)分别用(qk+1|k,sk+1|k(x))和(qk+1|k+1,sk+1|k+1(x))表示。从而可得

(24)

fk+1|k+1(Xk+1|Z1:k+1,u0:k)=

(25)

依据集合积分规则,式(23)中定义的回报函数φ可以简化为

φ(uk)=

(26)

依据式(20),最优控制动作可以表示为

(27)

现在通过SMC近似计算式(27)。计算所有测量数据对应的回报函数的均值作为φ(v)的值。Zk+1(v)是采用了控制动作v∈Uk后产生的预测测量数据集合,每一个Zk+1(v)都是由预测概率密度函数 (qk+1|k,sk+1|k(x))产生的。

式(26)中的积分记为

·[sk+1|k+1(x)]αdx

(28)

(29)

将积分代入式(26),每一个控制动作的回报函数的计算如下

(30)

综上,将φ(v)代入式(27)即可得到最优控制动作。

4 仿真实验

以反潜战中典型的舰艇反潜为例,验证基于动态数据驱动的反潜战仿真系统的可行性和有效性。主要是对数据同化算法和实时测量控制的实验,数据同化实验主要验证数据同化过程对仿真模型的校准效果,测量控制实验主要验证设计的测量控制方法的有效性。

4.1 数据同化实验

假设在反潜战系统中,潜艇匀速运动,速度近似5节,初始位置位于坐标(0,-8 000)(坐标单位:m)。反潜舰速度为4节,初始位置(0,0)m。扫描周期是30 s,探测概率近似高斯分布σD=5 000。每次扫描获得的杂波数服从泊松分布λ=1。数据同化过程的参数是:粒子数N=5 000,出生概率pb=0.01。

若探测传感器准确测量目标潜艇的位置(0,-8 000)m,通过潜艇仿真模型得到准确的轨迹为图2中蓝色轨迹,在此处假设为潜艇的真实轨迹。而这在现实环境中几乎难以做到,探测过程必然存在偏差。假设实际探测到潜艇的位置是(500,-8 500)m,通过潜艇仿真模型得到的轨迹为图中红色轨迹,很明显探测的误差使仿真模型运行的结果造成了很大的偏差,仿真结果甚至是不可用的。为仿真模型加入数据同化过程,将测量数据同化后作为模型的输入。如图2所示,绿色轨迹为同化后的仿真模型运行的潜艇轨迹,同样把存在误差的探测结果输入仿真模型,但一段时间后向潜艇真实轨迹接近并且逐渐收敛,仿真结果是有效可信的。对同化前后的潜艇位置进行误差分析对比,同化前探测误差对仿真轨迹造成的偏差越来越大,而同化过程不断校准仿真模型使位置偏差保持收敛,从而大大提高了仿真精确度。

图2 潜艇真实及同化前后仿真轨迹图Fig.2 Submarine’s real trajectory and simulation trajectorybefore, after assimilate

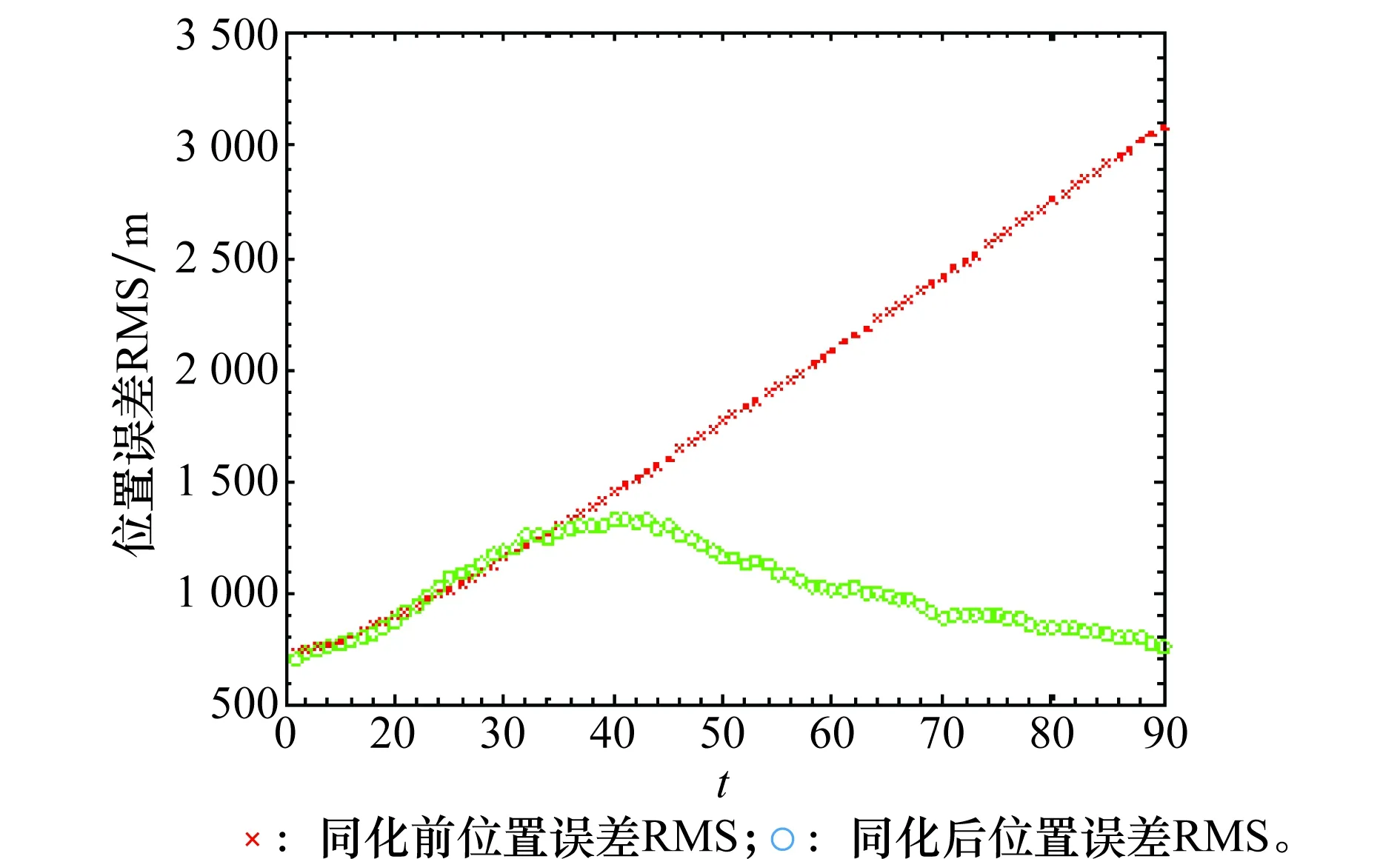
图3 数据同化前后误差RMSFig.3 Position Error before and after data assimilate

4.2 测量控制实验

在第1个实验的基础上,在t=51时刻加入测量控制过程,控制动作设置为对测量传感器的角度控制。反潜舰的速度是4节,朝向是-20°。行驶完一段之后,测量传感器根据回报函数调整角度以获取最优测量数据。pD,max=0.98表示传感器最大探测概率为0.98。以X轴正方向为0°,将角度范围确定在[-180°,180°)之间,以20°为间隔划分18个方向,从每个方向θ=-180°,-160°,…,160°中找出最优的角度。通过固定θ角获得t=51时刻的RMS位置误差,令500次蒙特卡罗仿真计算的误差平均值作为RMS位置误差。

实验计算的18个方向角度的RMS位置误差如图4所示,从-180°开始RMS位置误差逐渐增大,到20°时达到最大,然后一直到160°开始减小。RMS位置误差越小,则表示选取的角度越好,可知在t=51时刻将传感器角度调整为-180°为此时最优控制动作,传感器可以获取最优的测量数据。在500次蒙特卡罗仿真中,各个角度被测量控制算法选中的次数如图5。对应图4,位置误差越大的角度被选中的次数越小,最优角度-180°被选中了203次。通过实验表明测量控制算法能够为传感器获取最优测量数据提供有效可信的控制动作,即传感器调整的角度。

图4 不同角度RMS位置误差Fig.4 Position Error in different angle

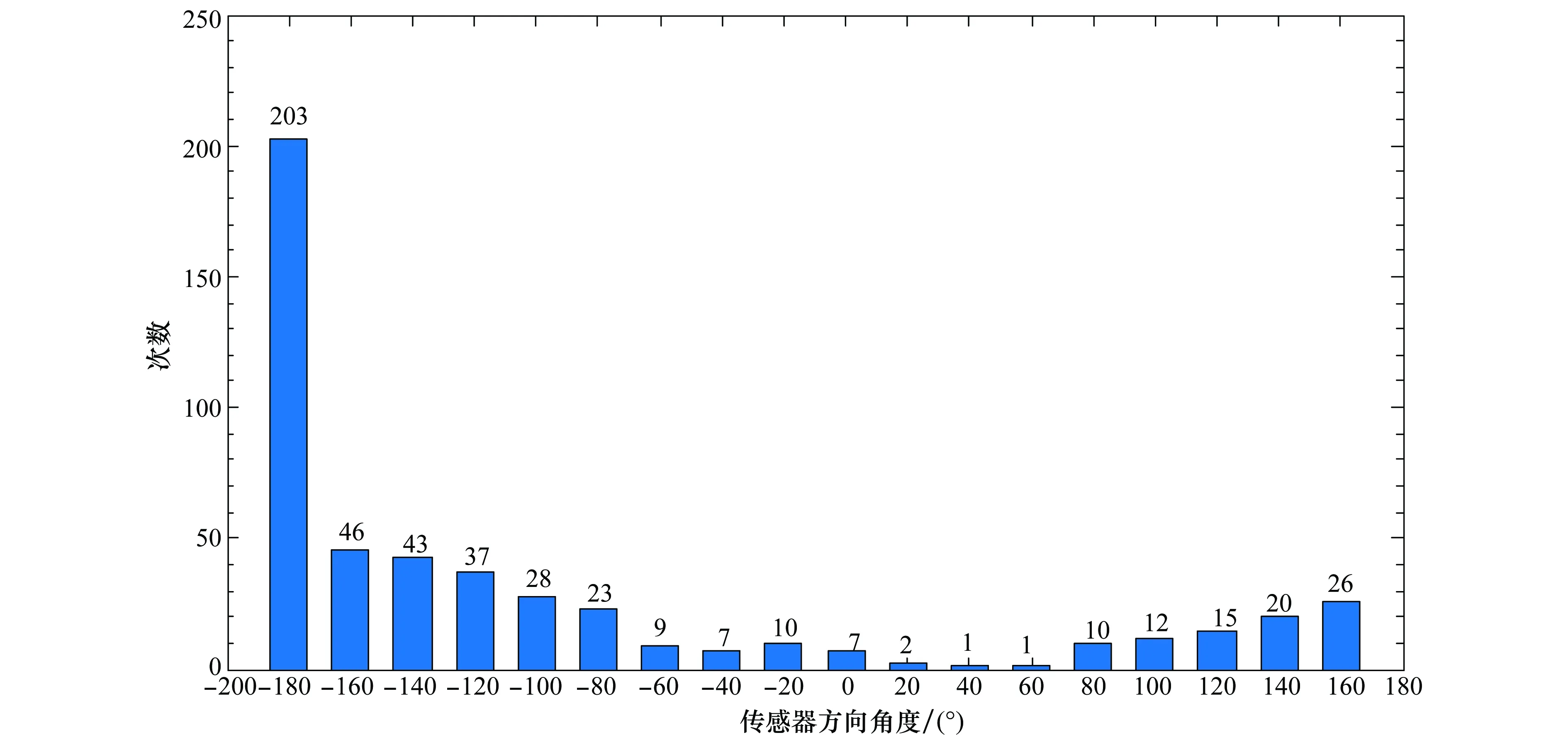
图5 测量控制算法的不同角度选择次数Fig.5 Number of different angles measurement control algorithm has chosen

5 结 论

基于动态数据驱动的反潜战仿真系统有效的将真实反潜战系统与虚拟反潜战仿真模型结合,使仿真可以在执行过程中动态地从真实系统接收数据并做出响应,反过来,仿真结果也可以动态地控制真实系统,指导测量控制过程。为完善改进目标潜艇的仿真模型,采用RFS理论构建仿真模型,能很好的描述现实战场空间中潜艇的存在状态。用粒子滤波的近似求解方法解决了基于RFS的潜艇状态方程无法求解析解的问题,建立评判传感器测量效果的回报函数,并确定最优控制动作。在舰艇反潜作战场景下,进行数据同化实验和测量控制实验,仿真结果表明提出的数据同化算法能够同化真实测量数据,提高仿真模型精确度,测量控制方法能够得到获取最优测量数据的传感器动作控制方案。本文设计利用数据同化算法和测量控制优化决策方法,形成了反潜战的DDDAS系统,提高对潜艇目标的探测精度。