基于原子范数的多跳频信号时频参数估计
2018-11-09东润泽张坤峰杨银松
东润泽, 郭 英,2, 张坤峰, 杨银松
(1. 空军工程大学信息与导航学院, 陕西 西安 710077; 2. 通信网信息传输与分发技术重点实验室, 河北 石家庄 050081)
0 引 言
跳频通信的侦察主要分为跳频信号检测、参数估计和网台分选3个部分[1-3],其中跳频信号的参数估计是对敌方跳频网台进行干扰的关键环节。近年来针对多跳频信号的参数估计主要包括时频分析[4-5]、稀疏重构[6-8]和原子分解[9-11]3种方法。时频分析方法通过得到清晰稳健的时频图然后实现对参数的估计,虽然一些改进的时频分布能抑制交叉项从而得到更加清晰的时频图,但是该方法依然存在对噪声敏感、跳频参数估计不准确的缺点。文献[6]通过在空间频率域构建超完备稀疏字典,利用稀疏贝叶斯重构信号完成频率参数估计,但未考虑频率不在字典网格上的情况。文献[7]通过稀疏重构来获取高聚集度的时频图,但只适用于在已知频率集中的信号。原子分解算法是通过构建原子字典来对接收信号进行表示,进而利用匹配跟踪(matching pursuit, MP)算法完成对跳频信号参数的估计,但是构造的原子字典是离散的,信号的参数空间却是连续的,在不知道信号先验信息的情况下很难构造出匹配的原子字典[12]。文献[13-14]提出一种基于稀疏线性回归(sparse linear regression, SLR)的参数估计方法,在低信噪比情况下能获得清晰的时频图,但在处理多跳频信号时信号配对存在困难。文献[15]针对有限网格与实际信号连续的参数之间存在的不匹配问题提出一种无网格压缩感知的方法,该方法思路新颖,在信号去噪[16-17]、波达方向(direction of arrival, DOA)估计[18-20]和雷达成像[21-22]等领域得到了广泛应用。
综上所述,目前对多跳频信号的参数估计主要是将信号的连续参数空间进行离散化,然后构建有限字典来对参数空间进行表示,并未考虑字典和信号不匹配的情况。针对该问题,本文在文献[17]基础上,利用跳频信号在时频域的稀疏性构造可以描述连续变量的无限原子集合,通过对接收信号进行重叠划分建立每段信号的原子范数最小化模型,通过求解其对偶问题完成对每段信号的估计,利用对偶多项式完成对每个分段信号的频率估计,再把每个分段信号内存在的频率合起来得到跳频信号频率集的估计,并通过统计各个分段内频率分量的数目完成跳变时刻的检测。
1 数学模型
1.1 跳频信号数学模型
假设在观测时间(0,T]内共有N个跳频信号,则接收信号可表示为
(1)
式中,sn(t)表示第n个跳频信号;cn表示第n个跳频信号的幅度;v(t)表示均值为零,方差为σ2的高斯白噪声。设第n个跳频信号sn(t)的跳周期为Tn,在观测时间内共有K个完整跳,第k(k=1,…,K)个完整跳的中心频率为fn k,初相为φn k,最开始非完整跳的持续时间为Δtn 0,中心频率为fn 0,初相为φn 0,则sn(t)可表示为
(2)
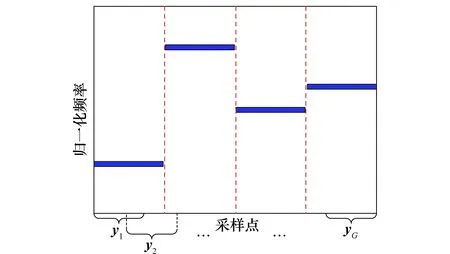
式中,rect(t)表示单位矩形脉冲函数,0 ,m∈(0,M] (3) 定义A为一个原子集合,假设A中的任一原子a不在其他原子构成的凸包conv(Aa)内,且凸包conv(A)是以原点为中心成中心对称的,即A中的原子都是凸包conv(A)的极值点,a∈A当且仅当-a∈A,则原子范数‖·‖A定义[23]为 ‖x‖A=inf{t> 0|x∈tconv(A)}= (4) ≤1}= sup{〈t,x〉|‖x‖A≤1}=sup{〈t,a〉|a∈A} (5) 根据跳频信号在时频域具有的稀疏性,首先定义原子集A中的原子[15]为 [a(f,φ)]h=ej2π(hf+φ),a(f,φ)∈CH (6) 式中,f∈[0,1]表示归一化频率;h∈(0,H]表示A中的原子是H维的复向量;φ∈[0,2π),则原子集A={a(f,φ)|f∈[0,1],φ∈[0,2π)}。 跳频信号具有在其持续时间内频率随机跳变的特性,为了使接收到的跳频信号能够被A中的原子所表示,需要对其进行等间隔划分,将长度为M的一段信号划分为G段长为H的信号,每段之间重叠长度为i,则有 (7) 将这G段信号按列组成观测矩阵Y=[y1,y2,…,yG],Y∈CH×G如图1所示。则式(3)可重写为Y=S+V,其中,S和V分别代表原信号矩阵和高斯白噪声矩阵,S=[s1,s2,…,sG],vg~N(0,σ2IH),vg∈V。 图1 跳频信号划分示意图Fig.1 Schematic diagram of frequency hopping signal division (8) 将式(8)转化为无约束最优化问题为 τ‖sg‖A (9) 式中,τ为正则化参数。 根据文献[17],原子范数最小化问题(9)的对偶问题为 (10) ,a(f,φ)〉= (11) (12) (13) u=[u1,u2,…,uN] ,tg〉 s.t.TH(Q)=e1 (14) 式(14)的对偶形式为 (15) 因此原子范数最小化问题(9)等价于 (16) (17) 图2给出了由截取的一段长为64点的跳频信号得到的对偶多项式的值,其纵轴以τ进行归一化,信噪比为10 dB。对每一段信号进行频率定位得到的频率分量取并集,我们就得到了跳频信号的频率集。 图2 基于对偶多项式的频率定位Fig.2 Frequency localization based on dual polynomials 假设观测时间T=5.12 ms,跳频信号个数N=3,采样率fs=200 kHz,采样点数M=1 024,3个跳频信号同步跳,频率集分别为[108,20,46,134]kHz、[46,130,96,160]kHz和[140,72,122,32]kHz,跳周期为1.28 ms,信噪比为10 dB。重叠划分得到的每段信号长为H=64,每段之间重叠i=32,则共有G=31段信号。对每一段信号分别进行频率定位,每一段信号对应的频率分量个数如图3所示。 图3 各段信号包含的频率分量个数Fig.3 Number of frequency components contained ineach segment of the signal 对所有分段信号的频率分量个数求平均,我们认为频率分量个数大于平均数的分段信号包含了跳变时刻,即第8,16和24段,取每一段的中心点为跳变时刻点,分别为第256,512,768。然后以检测出的跳变时刻点为边界,重新划分接收信号为4段,再进行频率定位,得到的时频图如图4所示。 图4 多跳频信号同步跳时频图Fig.4 Time frequency diagram for synchronous multiplefrequency hopping signals 设置3个跳频信号异步跳,频率集分别为[60,128,78]kHz、[154,180,104,40,162]kHz和[92,70,104,154,66,126,104]kHz,跳周期分别为2.33 ms、1.28 ms和1.04 ms,每个跳频信号第一跳的持续时间分别为275、153和155个采样点数,其他条件和信号划分方式同实验1,得到的时频图如图5所示。 为验证噪声对本文算法估计跳频频率的影响,设定信噪比从0 dB以1 dB为步长递增至10 dB,跳频信号个数N分别取2和3,其他条件和信号划分方式同实验1,取第一段长为64点的信号,在每个信噪比下进行100次蒙特卡罗实验,图6给出了归一化频率的MSE随信噪比变化的曲线。可以看出,本文算法对跳频信号频率的估计性能随着信噪比的增大而提高,当信噪比大于0 dB时,频率估计的MSE低于200 Hz。与文献[6]稀疏重构算法相比,本文算法的误差降低了一个数量级,与文献[10]原子分解算法相比,本文算法在相同信噪比下具有更好的估计性能。 图5 多跳频信号异步跳时频图Fig.5 Time frequency diagram for asynchronous multiplefrequency hopping signals 图6 频率估计均方误差随信噪比的变化Fig.6 Change of mean square error with signal to noiseratio of frequency estimation 本文从跳频信号参数估计的基字典不匹配问题出发,提出了一种基于原子范数的多跳频信号参数估计方法。该方法与以往方法相比不需要预先设定基字典,能够直接获得信号的频率集,而不是从跳频图案中对频率集进行估计,在低信噪比下具有良好的估计性能。
1.2 原子范数及其对偶范数

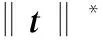
2 算法原理
2.1 原子范数最小化问题
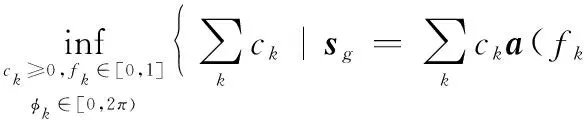
2.2 基于对偶范数的半定规划问题
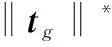




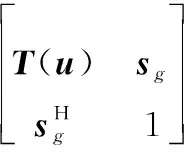
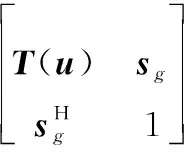

2.3 基于对偶多项式的频率定位


3 仿真实验与分析
3.1 实验1

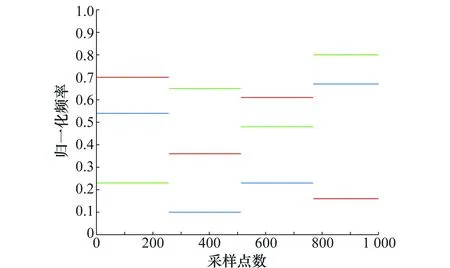
3.2 实验2
3.3 实验3


4 结束语
