基于干涉相位的两步法高精度无模糊时延估计
2018-11-09赵培焱彭华峰
赵培焱, 彭华峰, 邓 兵, 贺 青
(盲信号处理重点实验室,四川 成都 610041)
0 引 言
时延估计是现代信号处理的重要内容,广泛应用于无源定位、雷达声纳、导航遥测等军事领域,以及生物医学、工业探伤等民用领域[1]。经过多年发展,形成了以广义互相关[1](generalized cross-correlation, GCC)和互谱法[2]为代表的时延估计方法,并在实际工程中取得了广泛的应用。近年来,随着工程应用的深入和领域的拓展,对时延估计精度的要求也在不断地提高,如在航天测控等领域出现了一种以相时延为基本观测量的新型的高精度时延估计方法[3-4],并已经成功应用于实际任务[5-6]。但是,相时延估计面临整周模糊度解算的问题[3-6],往往需要对测控信号的频点[3,5-6]或测量基线[4]进行一系列特殊设计,且现有文献和实际任务中的方法[3-6]均无法一次性获得高精度且无模糊的时延估计。针对该问题,本文充分挖掘信号本身所携带的信息,提出一种两步法解决思路,第一步用大频率孔径获得低精度无模糊预估值,第二步利用该预估值引导解模糊,得到较为满意的估计结果,并通过仿真实验对所提方法的性能进行了评估。
1 信号模型
在无源定位、航天测控等领域,时延测量系统原理可以用图1表示。

图1 时延估计原理图Fig.1 Schematic of time delay estimation
两测站接收的信号模型可表示为
(1)
式中,s(t)表示目标源信号;r1和r2分别表示对应路径的衰减;τ表示信号到达两测站的时延;n1(t)和n2(t)为加性高斯白噪声,n1(t)和n2(t)不相关且分别与源信号s(t)不相关。
对接收信号进行采集,且忽略两站同步误差,可得
(2)
式中,n=0,1,…,N-1,N为信号采样点数。
对采样后的信号做N点DFT可分别得到离散频谱为
(3)
式中,k=0,1,…,N-1,N为DFT点数;S(k)=DFT[s(n)],Yi(k)=DFT[yi(n)],Ni(k)=DFT[ni(n)],i=1,2。
用X(k)表示两信号的互相关谱(简称互谱)可得
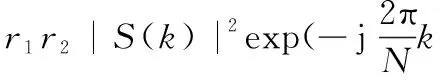
(4)
式中,k=0,1,…,N-1,N(k)为总噪声;根据加性高斯白噪声的特性,N(k)也为加性高斯白噪声,可以表示为
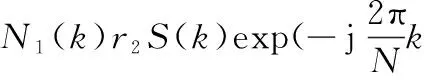
(5)
式(4)中所示的互谱,如暂不考虑噪声的影响,可以从结构上分为两部分,即互幅度谱和互相位谱,分别用A(k)和Ф(k)表示,即
A(k)=r1r2|S(k)|2,k=1,2,…,N
(6)
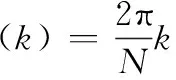
(7)
从式(7)中可以看出,待估计的时延参数τ存在于互相位谱信息中。由于相位的周期性,所以在互相位谱中各个频点的相位均是局限于[-π,π]内的。记Wk为频点k相位的整周模糊度,则互相位谱的完整表达应为
Ψ(k)=Φ(k)+2πWk,k=1,2,…,N
(8)
2 不同时延定义的区别与联系
当信号通过某一传输系统(自由空间也可以看作是某种系统)或网络时,信号输出相对于输入总会产生时间滞后,这就是系统时延。根据信号处理的不同应用场景,时延有不同的定义,比较常见的有包络时延、群时延和相时延。
包络时延[7]:调制信号经过传输系统,输出信号包络相对于输入信号的时间延迟。其表达式可表示为
(τ)|
(9)
式中,Ry1y2(τ)为信号的相关函数,其表达式表示为
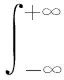
(10)
群时延[7]:调制信号通过传输系统时,单位频率上信号相位产生的延迟,即相位对频率的微分。其理论表达式为
(11)
式中,φ(ω)为系统的相位响应函数。
相时延[7]:单一频率信号或群信号中某个单频分量通过传输系统,输出信号相对于输入信号的滞后时间。表达式为该频率上的相位同该信号角频率比值为
(12)
上述3种定义分别是从不同的角度来描述时延,包络时延利用信号的幅度信息,群时延和相时延利用的是相位信息;从另一个角度来看,包络时延是在时域处理,群时延和相时延是在频域处理。式(11)是从微分定义出发定义群时延,但实际工程中不便于具体计算,从测量角度定义群时延为[7]
(13)
从式(13)出发并借助频率孔径(Δω)的概念,可以将时延的3种定义统一起来。
性质1对于非色散系统,当Δω为信号整个带宽时,包络时延与群时延相等。
证明假设两路信号时延为τ(ω),根据互相关函数的定义式(10)有

(14)
将式(14)变换到频域,根据FFT的时移性质可得
X(ω)=FFT(Ry1y2(τ))=FFT(y(t-τ))[FFT(y(t))]*=
S(ω)exp(jωτ(ω))S*(ω)=|S(ω)|2exp(jωτ(ω))
(15)
在式(15)中提取互相位谱
φ(ω)=jωτ(ω)
(16)
当传输系统为非色散系统时
φ(ω)=jωτ
(17)
对式(17)的等号两端微分,即包络时延等于群时延。
证毕
性质2当Δω趋于0时,群时延等于相时延。可以从式(12)中直接得到,无需证明。
根据性质1和性质2,包络时延和相时延都可以看作是群时延的两种特例。在时延测量中,分辨率与精度是两个重要指标。根据式(13),在相位测量精度一定时,Δω的选择将直接影响群时延测量精度与分辨率。Δω越大,测量分辨率越高,但精度越低;Δω越小,测量精度越高,但分辨率越低[7]。无法仅通过一次测量获得分辨率和精度都足够高的时延估计,这是时延测量的基本矛盾。
3 基于干涉相位的两步法方案
3.1 两步法的基本思路
工程实践中,通常希望获得精度和分辨率都足够高的时延估计。但通过第2节的分析可知,无法仅通过一次测量就获得这样的估计值。另一方面,频率孔径Δω在时延测量中扮演中重要的角色。对于包络时延,Δω趋于信号全频段,此时分辨率最高,但精度最低;对于相时延,Δω趋于0,此时精度最高,但分辨率最低。这与现实经验并不矛盾,两个单频信号做互相关操作,理论上应当得到无数等幅度的“周期峰”,无法通过峰值搜索来确定时延。相关函数的“周期峰”和互相位谱丢失整数倍2π的现象,可以统称为整周模糊。如果借助某种方法预先将模糊度解算出来,便可以获得高精度、无模糊(高分辨率)的时延估计。
第2节包络时延、群时延和相时延的定义,尽管表达形式有所不同,但其理论上都是对同一物理量的表征,在统计意义上应该具有相同的期望值,即满足
(18)
式中,E(·)表示取期望。
根据上述分析,针对无法一次性获得高精度无模糊时延估计的问题,提出两步法解决思路。第一步利用大孔径(信号全频段)获得无模糊低精度的预估值,第二步用其引导小孔径(单一频率)模糊度解算,最终得到高精度无模糊的时延估计。
3.2 基于Kalman的滤波干涉相位误差消除
从式(17)中可以看出,互相位谱的干涉相位与频率呈线性关系,故也被称为“干涉条纹”,条纹斜率即待估时延。系统传播、同步偏差、设备热噪声等都可能使得干涉相位测量值与理论值存在一定偏差。在统计信号处理框架下,干涉相位可以看作一个随机过程,若其状态转移矩阵先验已知,就可以利用Kalman滤波器对信号进行滤波处理,以改善其信噪比。
根据Kalman滤波理论,状态转移方程与测量方程可以表示为
(19)
式中,wk-1和vk分别表示过程噪声和测量噪声,两者相互独立且均为零均值高斯白噪声;xk为频点k的状态向量,定义为
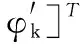
(20)
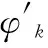
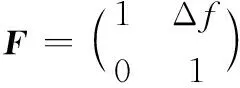
(21)
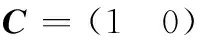
(22)
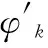
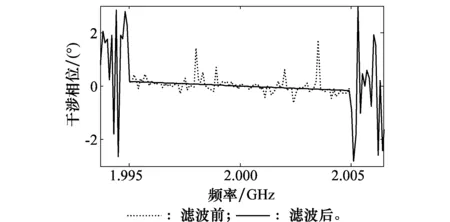
图2 滤波前后干涉相位对比图Fig.2 Comparison of interferometry phase before and after filtering
3.3 理论分析
利用预估值解模糊时,预估值精度需要满足一定的条件,方可保证解算的正确性。以群时延预估值为例,可以通过式(23)得到整周模糊的估计值。
(23)
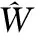
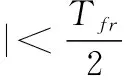
(24)
根据3σ准则,可以得出
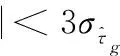
(25)
合并式(24)和式(25),可得
(26)
满足式(26)时,解模糊正确率理论上为99.7%。例如对于射频载频为2 GHz的信号,群时延预估值精度要求为±83.33 ps。在信号处理领域,克拉美-罗下界(Cramer-Rao lower bound, CRLB)是常见的理论下界。CRLB是在信息论的理论框架下推导的,与具体采用的方法无关,只与模型提供的信息量有关。传统一步法模型下的CRLB(single stage CRLB, SS-CRLB),可以表示为

(27)
式中,T为信号持续时间;B为带宽,信噪比(signal-to-noise ratio, SNR)。例如对于T=0.1 ms,B=10 MHz,SNR=10 dB的信号,CRLB为24.66 ps,满足式(26)的要求,采用适当的方法,能引导正确的模糊解算。
两步法模型中的第一步就是传统的模型,但第二步利用了信号的射频信息,以及待估值的结构信息,所以两步法模型信息量大于一步法模型。因此,两步法估计值理论上能突破SS-CRLB,这在第4节仿真部分将得到验证。
3.4 基于中位数信任域的统计方法
传统相时延估计方法中只利用率单一频点(如载频处)的相位进行估计,但实际工程中接收到的信号通常都是有一定带宽的,含有丰富的频率信息,传统方法的频带利用率显然不高;其次,只利用单一频点处的信息,估计结果易受相位噪声干扰,影响估计精度。为此,利用基于中位数信任域的统计方法[8]进行统计处理,进一步提升估计精度。该方法可表示为
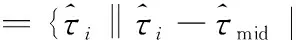
(28)
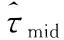
(29)
3.5 算法步骤
步骤1对两路接收信号做FFT,分别得其频谱;
步骤2利用两路信号频谱生成互谱,并提取互相位谱;
步骤3对互相位谱进行Kalman滤波,抑制相位噪声;
步骤4依据滤波结果得到时延预估值;
步骤5对信号频段内所有频点解算整周模糊,利用滤波后的干涉相位测量值得该频点上的相时延估计;
步骤6设定信任域半径,按照式(28)、式(29)对多个频点得到的估计值统计平滑,最终得到高精度无模糊的时延估计值。
上述步骤1~步骤4为本文定义两步法的第一步,对应大频率孔径;步骤5~步骤6为第二步,对应单频孔径,可见该方法综合了大、小孔径的优点。
4 仿真与分析
首先定义时延估计的均方根误差(root mean square error, RMSE)如式(30)所示
(30)

仿真实验1固定信号带宽和采集时间比较不同方法均方根差(root mean square error, RMSE)随SNR的变化情况。条件设置为:信源编码采用二进制频移键控(binary phase shift keying, BPSK),码元速率为10 Mbps,射频载频为2 GHz,采样率为5 GHz,信号采集时间为0.1 ms,真实时延设为30倍采样间隔,即τ=6 ns,第二步统计过程中的信任域半径D=10 ps。SNR从0~30 dB,每隔3 dB取一个值进行1 000次蒙特卡罗实验,统计RMSE变化曲线如图3所示。
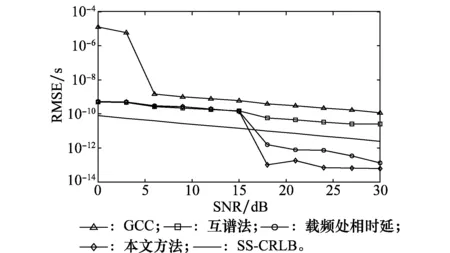
图3 不同算法RMSE随SNR变化曲线对比Fig.3 Comparison of changes of RMSE with SNR
仿真实验2固定信号SNR和采集时间比较不同方法RMSE随信号带宽的变化情况。基本条件设置同实验1,SNR设为20 dB,信号带宽从0~30 MHz,每隔2 MHz取一个值进行1 000次蒙特卡罗实验,统计RMSE变化曲线如图4所示。
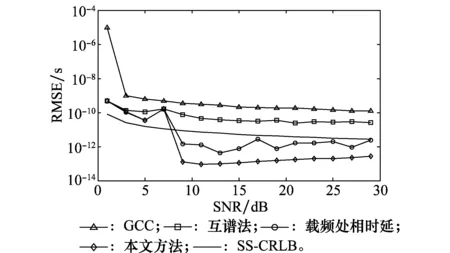
图4 不同算法RMSE随带宽变化曲线对比Fig.4 Comparison of changes of RMSE with bandwidth
需要注意的是,由于相位对噪声的敏感性,为保证估计的准确度,实际系统中需采用高精度的时频同步方案,如基于光纤连接线的时频传递方案[9]。为简化仿真中采集的同步过程,采用射频直采的方式。
从图3和图4中可以看出,本文方法估计精度明显优于对照方法,包括经典的GCC法,互谱法以及文献[3]中的单一载频处的相时延法。参与比较的还有式(27)所示的SS-CRLB。
图3中在SNR低于15 dB的区域,GCC方法精度最低,本文方法、互谱法以及载频相时延法性能差别不大,且都在SS-CRLB范围内;随着SNR的逐渐增大,所有方法的精度都有所提升,其中GCC法和互谱法的增长趋势同SS-CRLB一致,这和理论分析相符,但载频相时延法和本文方法却突破了SS-CRLB,其原因已在第3.3节中描述。进一步看出,本文方法的精度优于载频相时延法,得益于在信号频段内所有频点处都进行了估计,并引入了统计平均的过程,一定程度上平滑了相位噪声的影响。图4中以带宽为7 MHz为界分为了两部分,在小于7 MHz的区域,现象同图3相仿;大于7 MHz的区域却有所区别,载频相时延以及文本方法估计精度不再随带宽的增加而有明显提升,后者精度同样优于前者。综上,本文方法实现了高精度无模糊的时延估计,性能优于传统方法,对于10 MHz的信号,SNR高于18 dB时,估计精度优于1 ps。
5 结 论
借助频率孔径的概念,将包络时延、群时延和相时延的定义统一起来,揭示了分辨率与精度的矛盾是时延测量领域的基本矛盾。针对无法通过一次测量得到分辨率和精度都高的时延估计,提出两步法解决方案。第一步用大孔径获得无模糊、低精度的预估值,第二步利用预估值引导高精度相时延模糊度解算,最终得到高精度、无模糊的估计值。在第一步中,利用Kalman滤波器改善干涉相位抗噪声性能;在第二步中充分利用信号频段内丰富的频率信息得到多个估计值,采用基于中位数信任域的方法对多个结果统计平均,提升了频带利用率,进一步提高了估计精度,对于10 MHz的信号,SNR高于18 dB时,估计精度优于1 ps。该方法简单可靠、运算量小,具有较高的工程应用价值。低信噪比和窄带条件下高效的解模糊方法是下一步研究重点。
