数据丢包环境下的多传感器协同跟踪策略研究
2018-11-09高晓光万开方
高晓光, 李 飞, 万开方
(1. 西北工业大学电子信息学院, 陕西 西安 710129; 2. 电子信息控制重点实验室, 四川 成都 610036)
0 引 言
随着军事技术的发展,集团化、规模化、信息化作战逐渐成为现代战争的主要形式,尤其是制信息权,更是成为决定战争成败的关键。要实现对多个来犯目标的有效拦截,及早发现目标并对其稳定跟踪是关键。在综合利用多传感器对目标进行探测和跟踪过程中,为实现资源的高效利用,提升对目标的跟踪效果,获得信息优势,需要对有限的传感器资源进行动态的资源管理与协同跟踪调度[1]。
关于多传感器协同跟踪调度问题,已有众多文献对其进行过研究。文献[2]基于信息熵理论提出了多传感器管理算法,建立了相应的目标模型并给出了求解算法;文献[3]将目标权重与信息熵理论相结合,考虑目标不同威胁度值的不同,最终给出了基于目标权重的多传感器多目标跟踪信息熵模型;文献[4]基于信息理论提出了基于分辨力的传感器分配模型,并且给出了重加权多模型滤波模型,弥补了多模型滤波模型的缺陷;文献[5]给出了基于克拉美罗下界的多传感器管理模型,克拉美罗下界为滤波的理论下界,因此在进行跟踪资源协同分配时无需考虑滤波方法的选择;文献[6]基于弹道导弹防御系统,给出了基于该系统的多传感器跟踪框架;文献[7]建立了基于Renyi信息差理论建立了多传感器管理模型,并给出了相应的求解算法;文献[8]将伯努利滤波应用到多传感器多目标跟踪过程中,同时基于Renyi信息差理论建立了目标模型,针对多目标跟踪具有很好的效果。
综合分析现有研究不难发现,现有传感器协同调度问题的研究主要集中在传感器分配策略上,即假定数据可以成功传输到融合中心。然而在实际战场环境中,由于天气,地形等电磁环境的影响,特别是敌方电子干扰的存在,使得跟踪传感器的测量数据在远距离传输过程中很容易发生数据丢包,不能成功地传输到融合中心。这种在传输过程中造成的数据损失势必会对最终的融合结果以及传感器调度策略造成影响。因此,数据丢包环境下的多传感器协同控制问题成为实际战场环境中亟需解决的问题。
目前对这类数据丢包环境下的多传感器协同控制问题尚缺乏足够的研究。文献[9]研究了数据丢失的概率模型,但并没有给出数据补偿,这样并没有消除数据丢失对融合结果的影响。本文在文献[9]的基础上,讨论了造成数据丢包的几种情况,给出了几种丢包模型,同时分别制定了相应的补偿策略,最后给出了仿真验证,证明了这种补偿策略的有效性。
1 问题描述
考虑如下作战想定:在空中预警系统中,由一架预警机和多架侦察机组成的作战编队对入侵目标进行跟踪[10]。某一时刻,传感器探测到NT个入侵目标。探测传感器将目标信息传输给控制中心,控制中心将目标信息传输给预警机,并由预警机控制多架侦察机对入侵目标进行跟踪,如图1所示。初始时刻,预警机分配传感器对目标进行探测,传感器将探测信息传输给预警机,预警机根据一定的优化准则重新制定传感器目标配对策略,并重新组合传感器对目标进行照射。重复以上过程,直至跟踪精度满足要求为止。同时,在实际战场环境中,由于电磁干扰等因素的存在,使得侦察机上的传感器的测量数据不能及时有效的传输到预警机,即发生数据丢包,从而影响最终的跟踪精度。因此,必须制定一定的丢包补偿策略,以防止因数据丢包导致的目标失跟。

图1 作战想定示意图Fig.1 Description of Missile Battle Scenario
通过以上描述可知,该跟踪优化问题是一个多传感器多目标决策问题。首先对数据丢包进行描述,建立丢包模型;然后给出丢包补偿策略,当发生数据丢包时,应基于相应的补偿策略进行数据补偿,使数据丢包带来的损失降至最低;最后给出求解算法,基于以上思路,本文建立了问题求解模型,并给出了相应的求解算法和最终的仿真验证。
2 目标建模
2.1 数据丢包环境下协同跟踪控制架构
在集中式传感器管理框架中,丢包环境下的协同控制结构分为两部分:跟踪策略制定部分和跟踪策略执行部分,如图2所示。
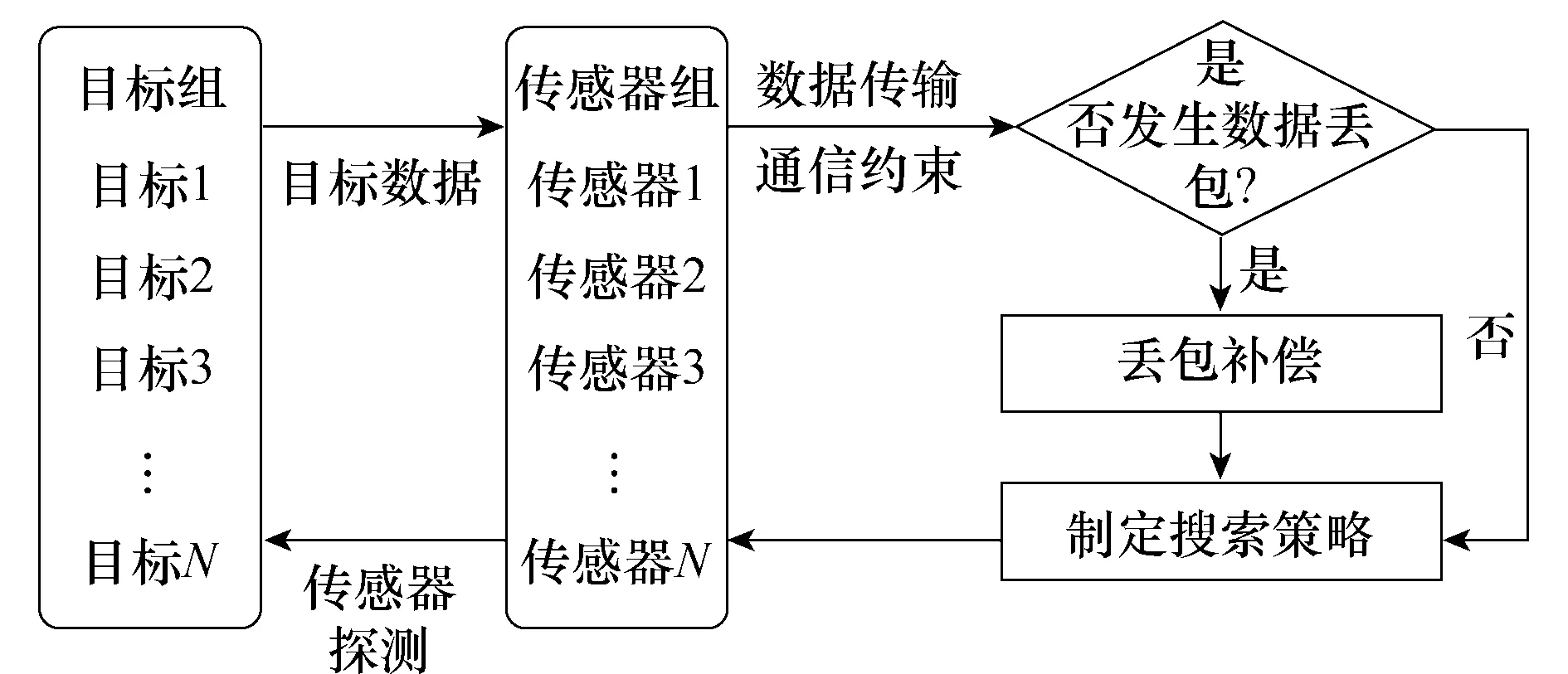
图2 控制架构图Fig.2 Control architecture
数据丢包条件下,融合中心在接收到传感器测量的目标实时数据之后,首先判断是否发生了数据丢包,如果数据接收正常,则直接根据既定的优化准则制定搜索策略;如果发生数据丢包,则调用丢包补偿算法,通过既定的丢包补偿策略修补数据,然后将修补后的数据输入到搜索策略制定模块,根据既定的优化准则制定搜索策略。最后,融合中心将搜索策略传输到传感器组,各传感器根据接收到的搜索策略重新组网,对目标进行重新扫描。以上过程重复循环,直到完成整个跟踪任务。整个任务规划伪代码如下:
Mission Planning
①Fori=1 toNdo
②Input: Target Data
③ifTarget Data is losing
④ Data compensate;
⑤endif;
⑥Strategyplanning;
⑦Output: strategy;
⑧endfor;
2.2 数据丢包模型及补偿策略制定
数据丢包是指在数据传输时,数据不能传输到融合中心或只能部分地传输到融合中心。造成数据丢包的原因主要有3方面:①战场复杂的环境,在实际作战过程中,由于天气、地形等复杂环境的影响,使得探测数据不能准确传输的融合中心,甚至造成数据丢失;②敌方干扰,是指敌方对我方施加一定的电子干扰,影响我方的数据通信链路,从而造成数据丢包;③通信带宽的限制,由于我方融合系统通信带宽的固有限制,使得同一时刻只能允许特定数量的数据通过,即只有部分测量数据能够传输到融合中心。基于以上描述,建立数据丢包模型。
定义随机变量ηi来表示传感器i的数据传输情况。若测量数据成功传输到融合中心,则ηi=1;若测量数据没有传输到融合中心,则ηi=0。且ηt满足伯努利方程[11],即
(1)
式中,λi为传感器测量数据成功传输到融合中心的概率,如图3所示。

图3 传输示意图Fig.3 Transmission schematic
本文假设各个传感器成功传输的概率是相同的,即λ1=λ2=…=λi=…=λn=λ。
如图3所示,各传感器对指定目标进行测量,并将测量数据传回到融合中心进行融合处理,以实现对目标的跟踪。设目标的状态方程和各传感器的非线性观测方程[12-13]分别为
(2)
对式(2)进行线性化处理得
(3)
(4)
式中,X(tk)表示tk时刻的目标状态向量;w(tk)是系统的白噪声向量,其协方差矩阵为Q(tk);F(tk)∈Rn×n是tk时刻的状态转移矩阵;G(tk)∈Rn×n是tk时刻的输入分布矩阵;Zj(tk)表示tk时刻第j个传感器的量测向量;vj(tk)是量测噪声,其协方差矩阵为Rj(tk);H(tk)是观测方程的观测矩阵噪声;vi,vj和w相互之间统计独立,且与初始状态X(t0)无关。
当发生数据丢包时,融合中心不能准确获得传感器测量的目标数据。如果直接剔除该传感器,则由于数据缺失使得融合结果不准确,最终导致跟踪精度降低。因此,本文提出了数据丢包后的补偿策略。以每个传感器为基本补偿单位,分为如下两种情况进行讨论。
(1)单个传感器跟踪单个目标。在这种情况下,如果发生数据丢包,则融合中心将完全失去目标当前时刻的观测值,从而导致跟踪失败。因此,要想在数据丢包的情况下继续保持对目标的跟踪,必须对当前时刻的测量数据做出合理估计。基于以上描述,本文给出了相应的补偿策略。当单个传感器跟踪单个目标时,若发生数据丢包,则把该目标上一时刻对下一时刻即当前时刻的预测值,作为当前时刻目标测量数据的估计值,以此来替代丢包数据,完成对丢包数据的重构。并把重构数据用于最后的数据融合处理,完成数据补偿。
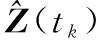
(5)
(2)多个传感器跟踪单个目标。在这种情况下,对该目标进行跟踪的传感器集合中,设其中一个或几个传感器的测量数据在传输过程中发生数据丢包,其他传感器数据传输正常。在这种情况下,应对发生数据丢包的传感器的测量数据做出合理估计。根据以上描述,本文给出的补偿策略是,当某个传感器的测量数据发生丢包时,把该目标上一时刻对下一时刻即当前时刻的预测值,和其他正常工作的传感器获得的目标当前时刻的测量值,进行加权求和,作为丢包数据的估计值,以此完成丢包数据重构。对重构数据进行滤波,即数据补偿。
设某一时刻tk有n个传感器同时跟踪一个目标。在测量数据传输到融合中心的过程中,传感器ni(i=1,2,…,n)发生数据丢包,其他传感器的测量数据分别为Znj(tk),j=1,2,…,n且j≠i。对于传感器ni,其上一时刻tk-1预测的当前时刻的状态为Xni(tk),则最终得到的传感器ni的测量数据为该预测状态值与其他传感器的当前测量值的加权求和,即
κ1Zn1(tk)+κ2Zn2(tk)+…+
κiXni(tk)+…+κnZnn(tk)
(6)
式中,κi为权值,满足
0≤κi≤1

(7)
综上,可以得到某传感器用于最终跟踪融合滤波的观测数据为
(8)
2.3 数据丢包环境下的序贯扩展卡尔曼滤波模型
序贯扩展卡尔曼滤波是用多个传感器的测量值对目标的状态进行估计的一种融合算法[14]。其基本思想是:对每一个传感器运行一个独立的扩展卡尔曼滤波器,对其进行排序,然后依次将前一个滤波器的状态估计值作为下一个滤波器的状态预测值。本文在第2.2节给出的丢包模型下,推导出数据丢包环境下的序贯扩展卡尔曼滤波模型。
根据上节给出的目标状态方程和观测方程,首先给出状态一步预测值x(tk)和预测误差协方差矩阵P(tk)为
x(tk)=F(tk-1,tk)x(tk-1)
P(tk)=F(tk-1,tk)P(tk-1)FT(tk-1,tk)+…+
G(tk-1,tk)Q(tk-1,tk)GT(tk-1,tk)
(9)
设某一时刻有n个传感器对某一目标进行跟踪测量,下面给出相应的序贯状态估计:
x(tk)=(x(tk))n,i∈n
(10)

(11)
状态估计协方差矩阵P(tk)为
(12)
2.4 基于信息熵的多传感器协同跟踪控制规划模型
Shannon用发生概率的倒数来表示一个事件的信息,假设每一个事件的发生概率为pi,则信息定义[15]为
ΔI(pi)=lg(1/pi)=-lg(pi)
(13)
那么信息熵定义为信息的期望值,即
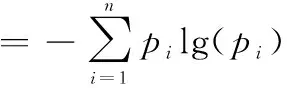
(14)
信息熵只描述了系统的不确定性,并不能反映信息量的大小。因此,用量测前后信息熵的差值即信息增量来表征信息量的变化,即
I=H(k|k-1)-H(k|k)
(15)
跟踪任务下,目标的不确定性可以用目标量测前后的滤波协方差矩阵表示,由此可得跟踪任务下信息增量的形式为
(16)
式中,‖cP‖为协方差阵的矩阵范数
在实际计算中,只需要信息增量的相对大小,并不需要其绝对值。因此,可以用矩阵范数的变化来近似表示信息增量,即
I=‖cP(k|k-1)‖-‖cP(k|k)‖
(17)
为简化计算,可以用矩阵的迹替代矩阵范数近似计算,即
I=tr{cP(k|k-1)}-tr{cP(k|k)}
(18)
设有M个传感器同时跟踪N个目标。M个传感器组网对目标进行跟踪,共有2M-1个子传感器网络Si。i∈2M-1跟踪策略即在充分考虑目标威胁度值的同时,尽量减少目标状态的不确定性,即使得每次量测前后的信息增量最大。因此,以目标威胁度值为权值,结合得到的信息增量,得到基于信息熵的传感器跟踪管理任务模型为

(19)
式中,mi为目标i的威胁度值;Iimax为传感器组网对目标i进行跟踪测量所能获得的最大信息增量;si表示子传感器网络;[si]表示组成子传感器网络si的传感器的个数。约束条件表示同一时间所有传感器都要工作,并且对目标i应至少有一个传感器对其进行照射。
3 算法设计
本文基于二值粒子群算法,设计了求解上述优化模型的算法。传感器对目标的照射只有两种情况,照射或者不照射。设照射为1,不照射为0,则每个粒子的每一位的取值只有两种情况,因此本文选取二值离散粒子群算法对问题进行求解。计粒子种群的大小为N=20。
由上面假设,二值离散粒子群算法的计算步骤如下:
步骤1初始化粒子群,对每个粒子进行二进制编码。
步骤2计算每个粒子的适应度值。本文中的适应度值为传感器对目标配对所获得的信息增量。
步骤3更新个体最优Pbest及全局最优Gbest
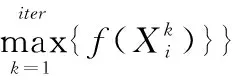
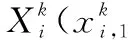
(21)
(22)
其中

(23)
步骤4更新速度,对每个粒子的每一位更新速度。首先计算每个粒子的每一位的速度

(24)
然后利用sigmoid函数将粒子速度映射到[0,1],即
Sig(vij)=1/(1+exp(-vij))
(25)
步骤5更新粒子位置:
(26)
式中,rand()是一个随机数,从区间[0,1]产生。
步骤6如果满足条件,则输出全局最优粒子值,并输出其对应的适应度值。否则转到步骤2,重复迭代。
算法流程图如图4所示。
4 仿真分析
4.1 仿真参数
仿真中,假设由5个传感器对3个运动目标进行跟踪。传感器为机载传感器,载机在指定区域作盘旋机动,对入侵的3个目标进行跟踪,并将测量的到的目标数据传递给融合中心,由融合中心制定搜索编队策略,然后传感器根据搜索策略重新进行测量。目标的初始数据由地面或空中融合中心传输给跟踪系统。假设笛卡尔坐标系下目标的机动模型为
(27)
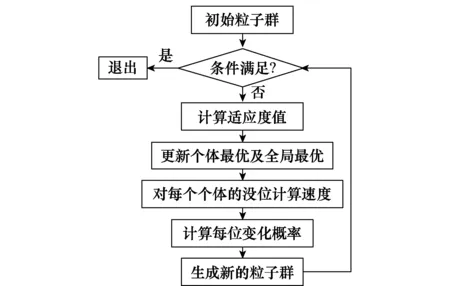
图4 算法流程图Fig.4 Algorithm flow
各目标的初始位置和速度参数如表1所示。

表1 目标初始参数
传感器在极坐标下的测量模型为
(28)
以传感器的位置为坐标原点,各传感器在笛卡尔坐标系下的初始位置如表2所示。

表2 传感器初始位置
各目标的状态转移模型为
F=[1,t,0,0;0,1,0,0,0;0,0,1,1;0,0,0,1]
初始协方差为
P=[100,0,0,0;0,0,0,0;0,0,100,0;0,0,0,0]
初始状态估计值为
仿真次数为100,采样周期为t=1 s。
4.2 仿真验证1:数据接收正常
正常情况下,传感器将测量得到的目标数据传输到融合中心,融合中心对目标进行滤波融合,并根据第3节提出的优化准则,制定新的搜索策略。传感器接收到新的搜索策略后,重新组网,继续对目标进行探测,直到完成跟踪任务,具体仿真结果如图5所示。
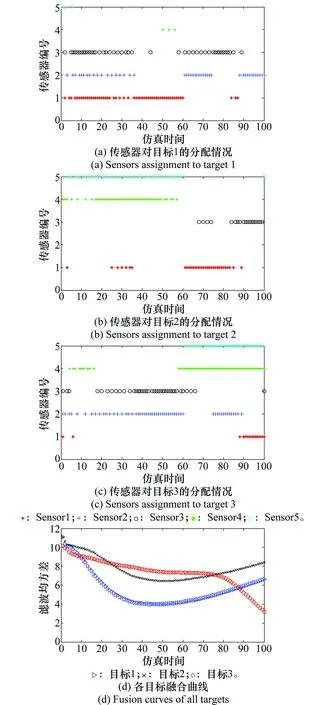
图5 数据接收正常时各目标仿真图Fig.5 Simulation chart of each target when data receives normal
图5给出了传感器对各个目标的分配策略,并给出了整个过程中各目标滤波均方差的变化情况。由图5可知,各目标的融合曲线很快收敛到稳定值,稳定后的滤波均方差小于10,完全可以满足实际作战需要。
4.3 仿真验证2:数据丢包
实际战场环境中,由于电磁干扰等不确定性因素的存在,造成传感器的测量数据在传输到融合中心的过程中发生数据丢包。假设在40~50 s时间段内,传感器1和传感器2发生数据丢包,其他条件不变,得到仿真结果如图6所示。
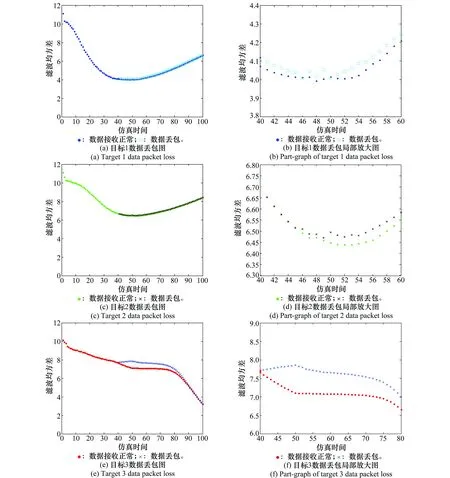
图6 数据丢包仿真结果Fig.6 Data packet loss simulation results
图6分别给出了目标1、目标2、目标3在数据丢包情况下的融合曲线和局部放大图,以及数据传输正常和数据丢包情况下传感器对目标的分配情况。通过目标数据丢包放大图可以看出,传感器1和传感器2发生数据丢包对各个目标均造成了不同程度的影响。通过对比丢包前后的仿真图可知,在数据丢包的40~50 s时间段内,传感器1和传感器2较少照射目标1和目标2,因此,目标1和目标2所受影响较小,丢包后融合曲线虽然发散,但并不是很大;在该时间段内,传感器1和传感器2主要照射目标3,因此数据丢包对目标3的影响较大。40~50 s内,融合曲线发散很大。
4.4 仿真验证3:丢包补偿
通过上面仿真可知,当发生数据丢包时,如果不进行补偿,最终的融合曲线将出现一定程度的发散,甚至会导致目标丢失,因此必须对丢包数据进行补偿。根据本文提出的补偿策略,给出丢包补偿仿真结果如图7所示。
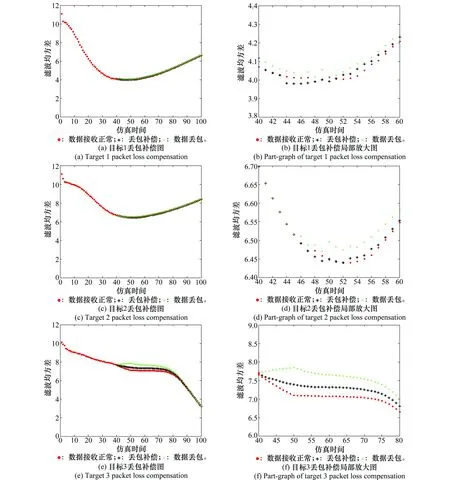
图7 丢包补偿仿真结果Fig.7 Packet loss compensation simulation results
图7(a)~图7(e)分别给出了各目标在丢包补偿策略下的融合曲线和局部放大图。对于目标1和目标2,虽然受数据丢包影响较小,但通过局部放大图可以看出,补偿后的融合曲线相对于补偿之前的融合曲线仍具有极好的补偿效果;对于受数据丢包影响较大的目标3,补偿策略具有显著的效果,不仅抑制了滤波曲线的发散,同时最终的融合曲线也非常接近正常情况下的融合曲线。由仿真结果可以看出,本文提出的补偿策略具有很好的补偿效果,可以有效的缓解短时间内数据丢包对最终融合结果所造成的不良影响,保证一定的目标跟踪精度。
图8和图9分别给出了丢包补偿前后传感器对目标的分配情况。对比丢包补偿前后传感器对目标的分配情况。在发生数据丢包的40~50 s时间段内,传感器1和传感器2更多地分配给目标1和目标2,而不是像丢包补偿之前那样全部分配给目标3,这样就有效地减小了传感器1和传感器2的数据丢包对目标3融合结果的影响,即通过其他目标的参与,使得更多的目标来分担数据丢包带来的损失,而不是只让一个目标来承担。对于目标3,在40~50 s时间段内,补偿之后传感器1和传感器2的照射时间相对于补偿之前大幅度减小,同时,剩余正常工作的传感器在该时间段内的照射时间相应增加。从而最终保证在数据丢包情况下,各目标的融合结果虽然受到一点影响,但是仍能保持在一定精度范围内,有效抑制了滤波发散,保证了目标的有效跟踪。

图8 数据丢包下传感器对目标的分配情况Fig.8 Distribution of the sensor to the target under the data packet loss
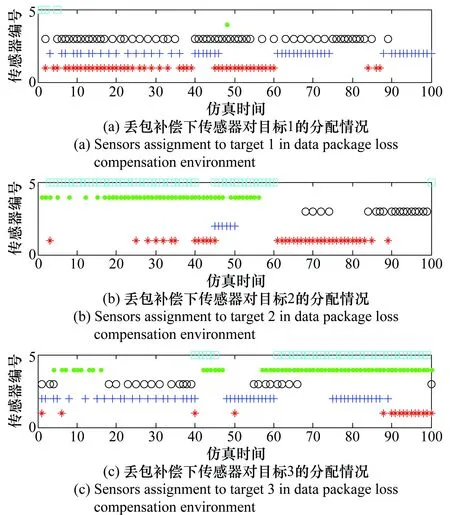
图9 丢包补偿下传感器对目标的分配情况Fig.9 Distribution of the sensor to the target under thepacket loss compensation
5 结 论
本文针对实际战场中复杂的电磁环境,首先分析了实际战场环境中传感器数据丢包对最终数据融合造成的影响,给出了数据丢包模型,然后根据两种不同的数据丢包模型,分别给出了数据丢包补偿策略。基于信息熵理论建立了数据丢包环境下的多传感器跟踪任务管理模型,并给出了基于二值粒子群的求解算法。最后通过仿真验证证明了本文提出了数据补偿策略的合理性和有效性,可以在实际战场环境中减小数据丢包带来的损失,有效抑制滤波发散,将最终融合结果保持在一定精度。
