基于Rayleigh衰落信道下MISO-MU-CSDCSK通信系统性能分析
2018-11-09许嘉平张天骐
张 刚, 许嘉平, 张天骐
(重庆邮电大学信号与信息处理重庆市重点实验室, 重庆 400065)
0 引 言
作为一种重要的非线性科学分支,混沌理论目前已经成为一门十分诱人的前沿课题[1]。混沌信号具有许多特殊性质及优点,例如:初始条件敏感性、非周期性、长期不可预测性、严格的自(互)相关特性、产生设备简单等,所以在保密通信中具有巨大的应用价值[2-5]。在典型的非相干混沌数字保密调制系统中,差分混沌移位键控(differential chaos shift keying, DCSK)[6]应用最为广泛,许多混沌调制系统都是基于该系统改进得到。DCSK系统在误码性能方面比相关延迟移位键控(correlation delay shift keying, CDSK)[7]具有优势,但是由于花费了一半的时间传输参考信号,所以传输速率较低。文献[8-10]提出了不同方案来解决DCSK传输速率低的问题。目前基于多用户混沌调制方案非常适合混沌通信发展的需求,具有更强的发展空间。文献[11]最早将多用户引入DCSK通信系统中,多址DCSK(multi-access DCSK, MA-DCSK)被提出;文献[12]对MA-DCSK系统展开了全面的性能分析。2002年,文献[13]提出了可变延迟多址DCSK(variant delay multiple access-DCSK, VDMA-DCSK)通信系统,该系统利用发送给每个用户的参考信号和信息信号之间的间隔均不相同来实现多用户传输。然而,以上多用户混沌键控通信系统均存在严重的用户间干扰问题,误码性能差,且需要大量的延迟电路造成系统设计复杂不易实现。为了解决上述问题,文献[14]提出了一种基于正交可变扩频因子(orthogonal variable spreading factor, OVSF)码的多址DCSK方案,并将其应用于射频识别(radio frequency identification, RFID)系统中。文献[15]提出了一种基于正交频分复用(orthogonal frequency division multiplexing, OFDM)的多用户DCSK通信系统,该系统表现出较好的误码性能,但是系统设计的复杂度太高。文献[16]提出了多用户分段移位DCSK(MU-SSDCSK)通信方案,通过消去码间干扰,增强了系统误码性能,具有一定的借鉴性。
将DCSK系统与多天线技术结合应用是目前混沌通信的热门问题。文献[17]提出了多输入单输出DCSK(multiple input single output DCSK,MISO-DCSK)。文献[18]提出了多输入单输出正交自参考DCSK(MISO orthogonal reference modulated DCSK, MISO-ORM-DCSK)。上述系统通过引入多天线技术都提高了系统的误码性能,所以MISO技术应用于混沌数字调制具有很好的前景。
为了更好的提高多用户系统的误码性能,本文提出了一种多用户循环移位DCSK(multiuser cyclic shift differential chaos shift keying, MU-CSDCSK)系统。首先,根据用户数量将延迟后的参考信号均分为N段,分段后的信号依次送入不同的循环移位器作为信息载体传播,利用Walsh码确保各用户传输信号严格正交。为了抑制信道噪声的影响,又深入分析了多输入单输出多用户循环移位DCSK(multiple input single output-MU-CSDCSK, MISO-MU-CSDCSK)系统。在Rayleigh衰落信道中对该系统进行了仿真分析,结果表明,该系统能够有效的改善误码性能,具有很高的应用价值。
1 基于DCSK的非相干混沌通信
1.1 DCSK通信系统
DCSK系统利用传输参考(transmitted reference, T-R)技术,将混沌参考载波信号和经过调制的信息信号传输到接收端。DCSK系统发射图如图1所示。DCSK系统的帧结构包括两个时间相同的时隙,前半部分传输混沌参考信号,后半部分传输信息信号。若bk=+1,两个时隙内的信号相同;若bk=-1,则两个时隙内的信号相反。
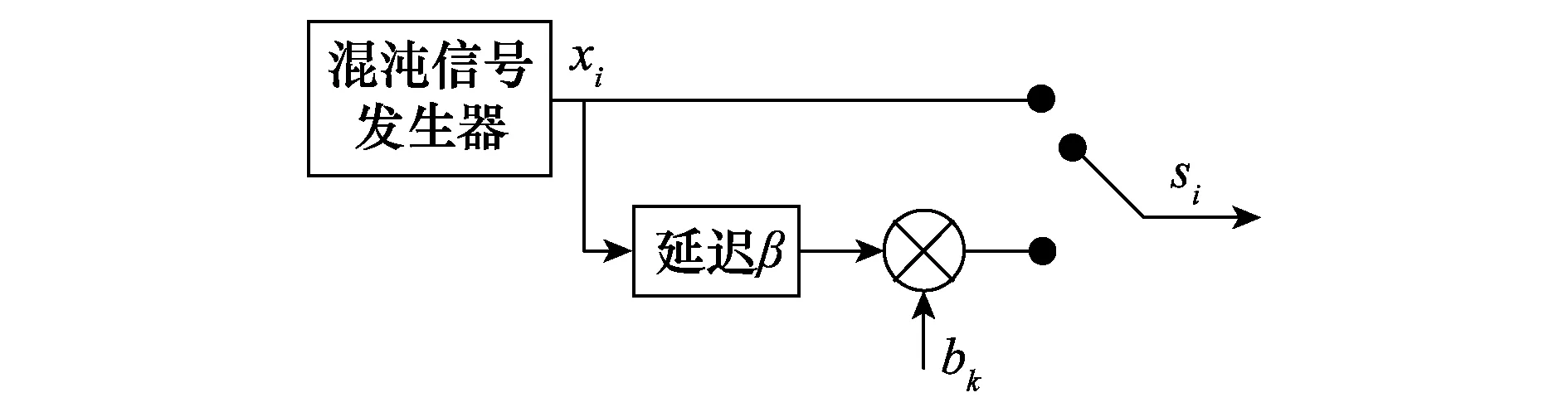
图1 DCSK系统发射图Fig.1 Transmitter block diagram of the DCSK
由图1可知DCSK系统的传输信号si可表示为
(1)
式中,xi为参考信号;i代表的是第i个采样点;bk为二进制信息;k代表的是第k个时间帧;β是混沌采样点数,根据扩频因子(spreading factor, SF)的定义,DCSK系统满足SF=2β。
为了恢复出信息bk,将接收信号ri与其延迟β后的信号ri-β作相关运算,并将运算值送入相关器判决。其接收图如图2所示。

图2 DCSK系统接收图Fig.2 Receiver block diagram of the DCSK
假设信号传输过程中只受到加性高斯白噪声(additive Gaussian white noise, AWGN)的影响,相关器输出结果Zk表示为
(2)
ri=si+ξi
(3)
式中,ri为接收信号;ξi为加性高斯白噪声。将式(1)、式(3)代入式(2)得
ξi-β)(bkxi-β+ξi)=
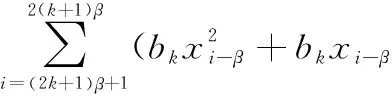
(4)
式中,第一项为均值不为零的有用信号;后三项为均值为零的噪声干扰项。所以最佳判决门限为零,若第一项为正,则传输信息bk=+1;若第一项为负,则传输信息bk=-1,即
(5)
1.2 MU-CSDCSK通信系统
Hadamard矩阵是一种正交矩阵,并且矩阵中的元素为“+1”或者“-1”。Walsh码可由多阶Hadamard矩阵展开取行得到,具有完美的互相关特性,能够有效抑制甚至消除多址干扰。利用下面所给的Hadamard矩阵构建一个2p阶的Walsh码,即
(6)
式中,p=1,2,……;W20=[1]为基础Hadamard矩阵。式(6)中的每一行都代表一个Walsh码序列,序列长度由Walsh码阶数p确定。
图3给出了MU-CSDCSK系统传输信号的帧结构图。每帧由两个长度为Ts时隙组成:参考时隙和信息时隙。参考时隙中,长度为β的混沌序列作为参考信号;信息时隙中,N个相同长度并携带不同二进制信息的混沌序列作为信息信号。DCSK系统中,传输1 bit的信息需要2Ts时间,而在MU-CSDCSK系统中,2Ts时间内可以传输Nbit的信息。因此,MU-CSDCSK系统可以获得比DCSK系统更高的传输速率。
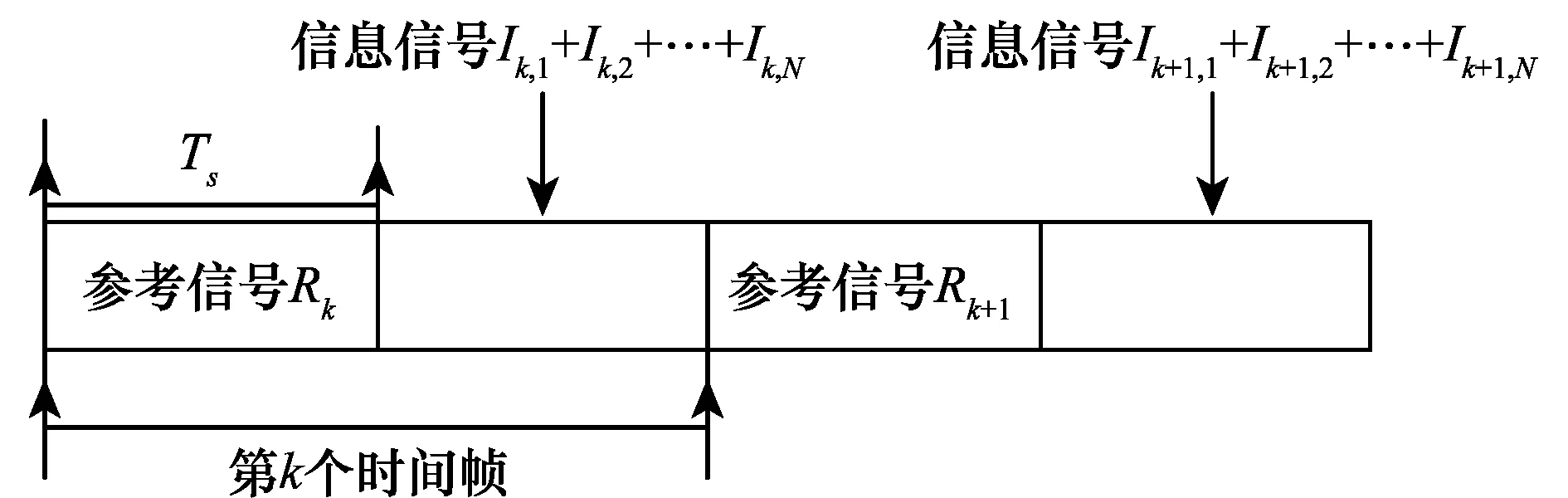
图3 MU-CSDCSK系统的帧结构Fig.3 MU-CSDCSK frame format
MU-CSDCSK系统的发射图如图4所示。首先混沌信号发生器产生一个混沌序列yi,k,yi,k经过符号函数生成归一化混沌序列xi,k,其映射表示为
,yi∈(-1,1)
(7)
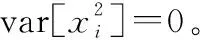
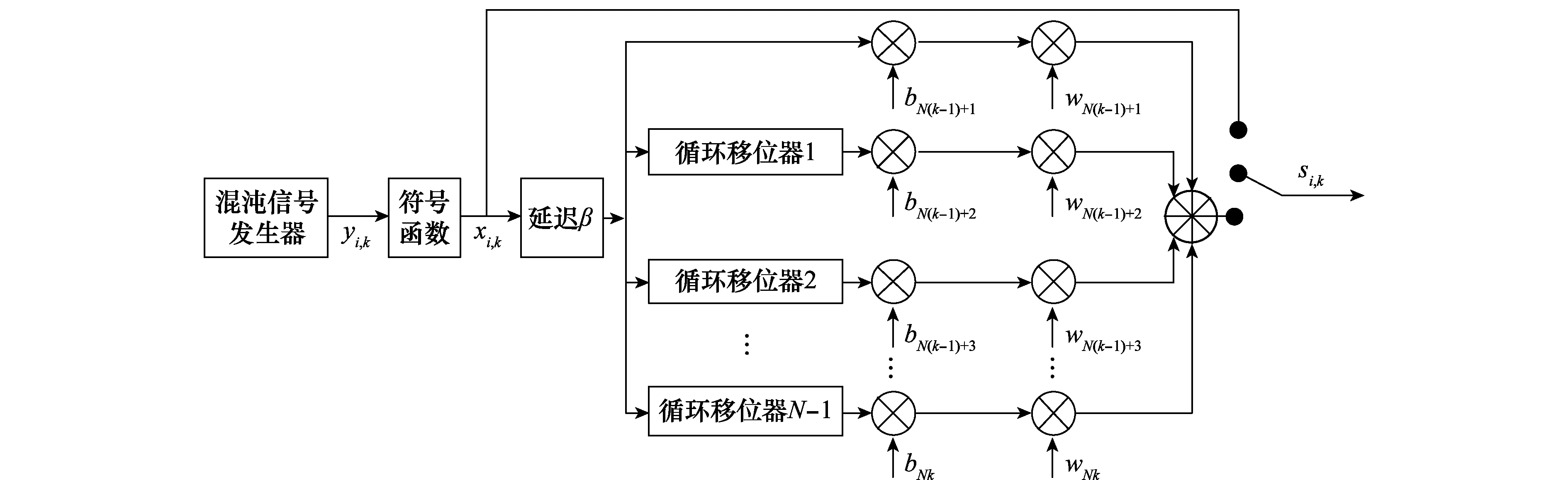
图4 MU-CSDCSK系统发射图Fig.4 Transmitter block diagram of the MU-CSDCSK
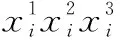
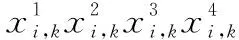
(8)
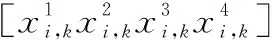
(9)
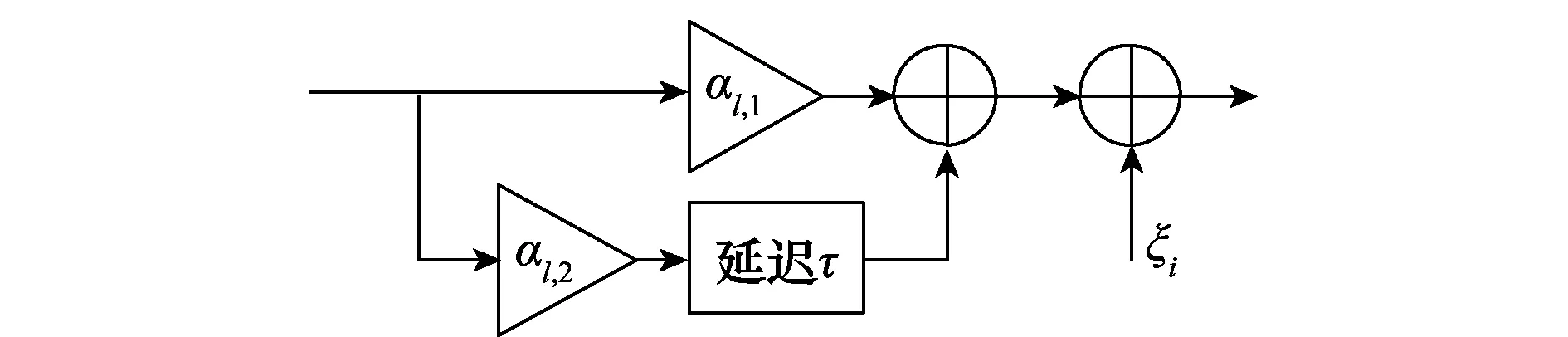
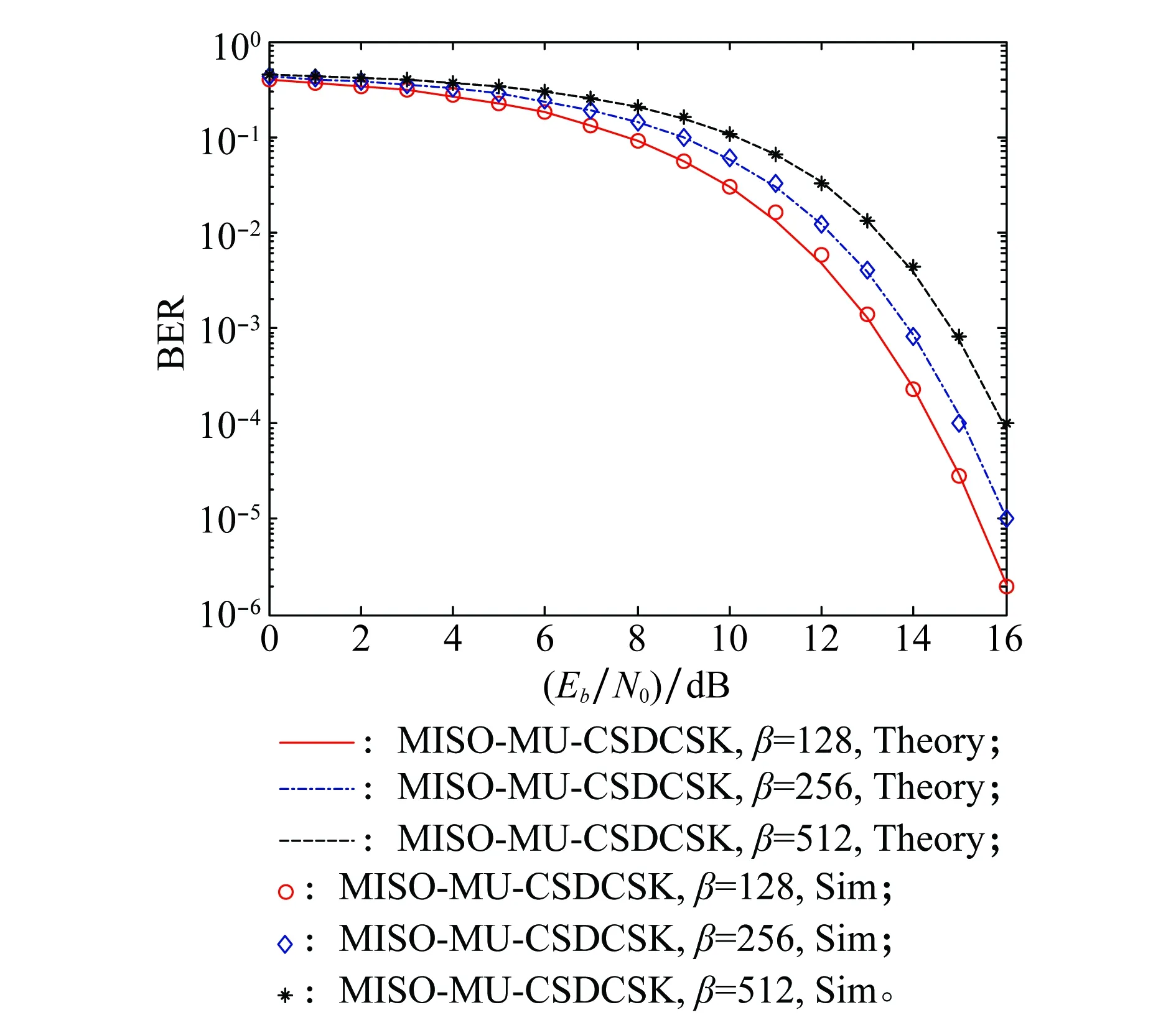
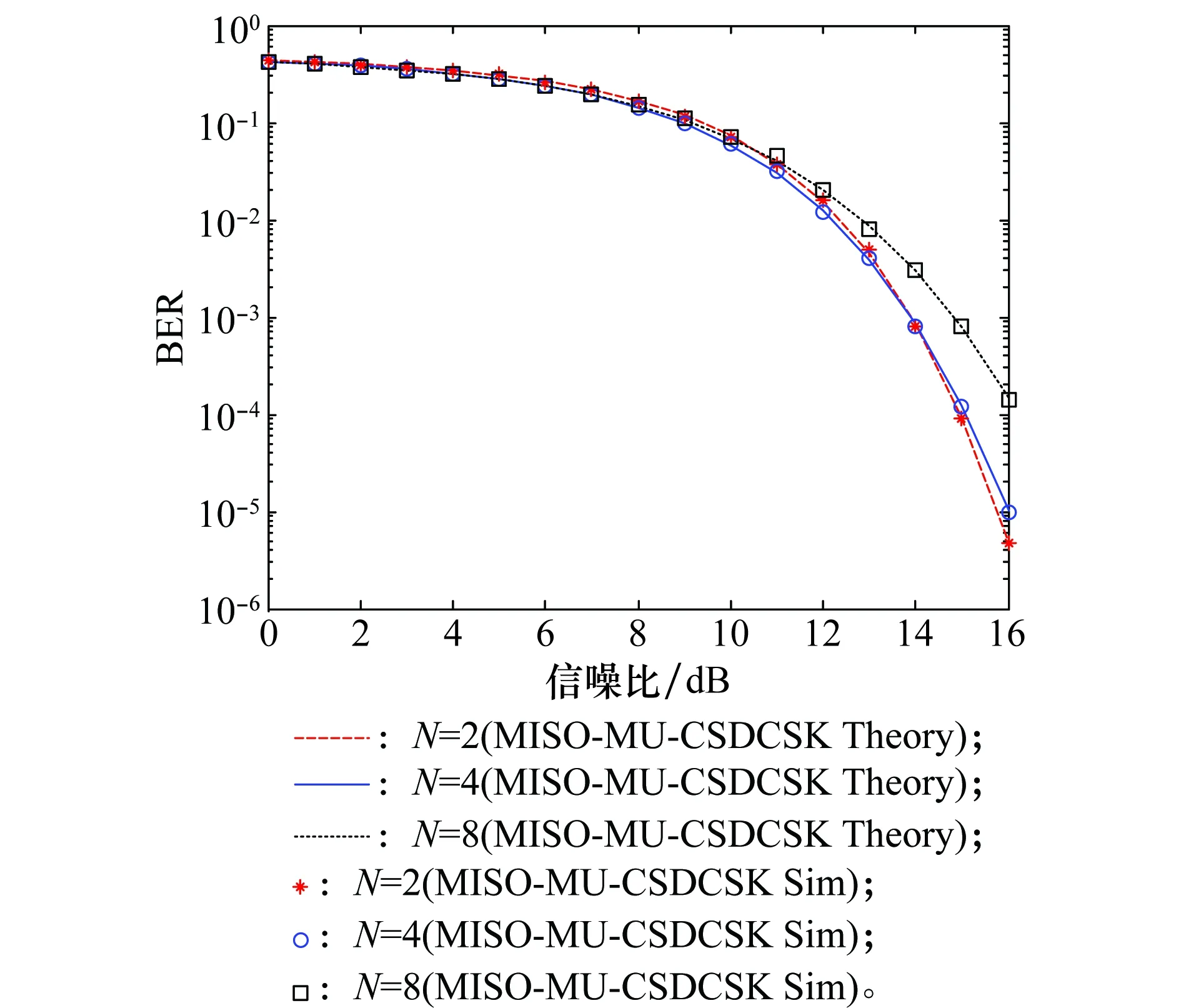
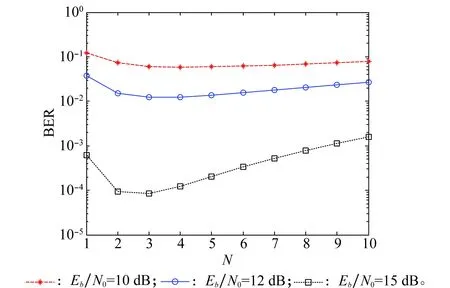
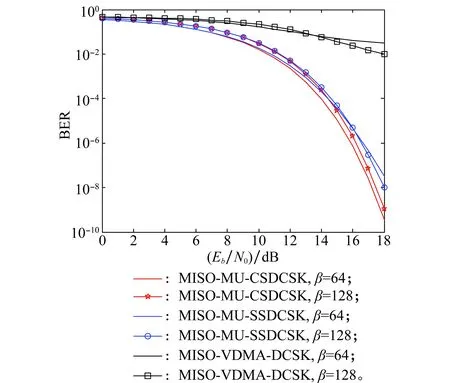
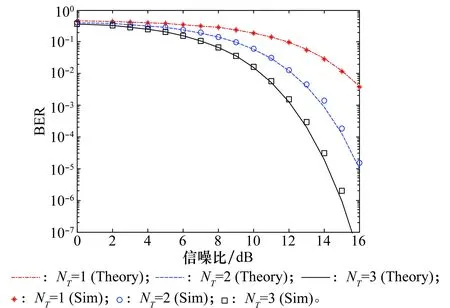
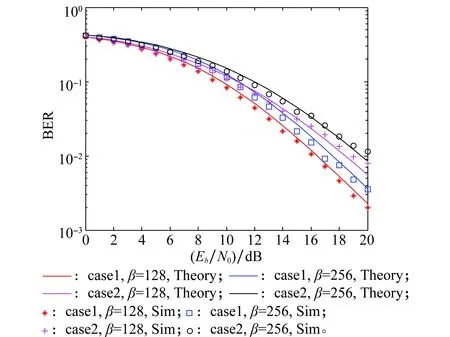
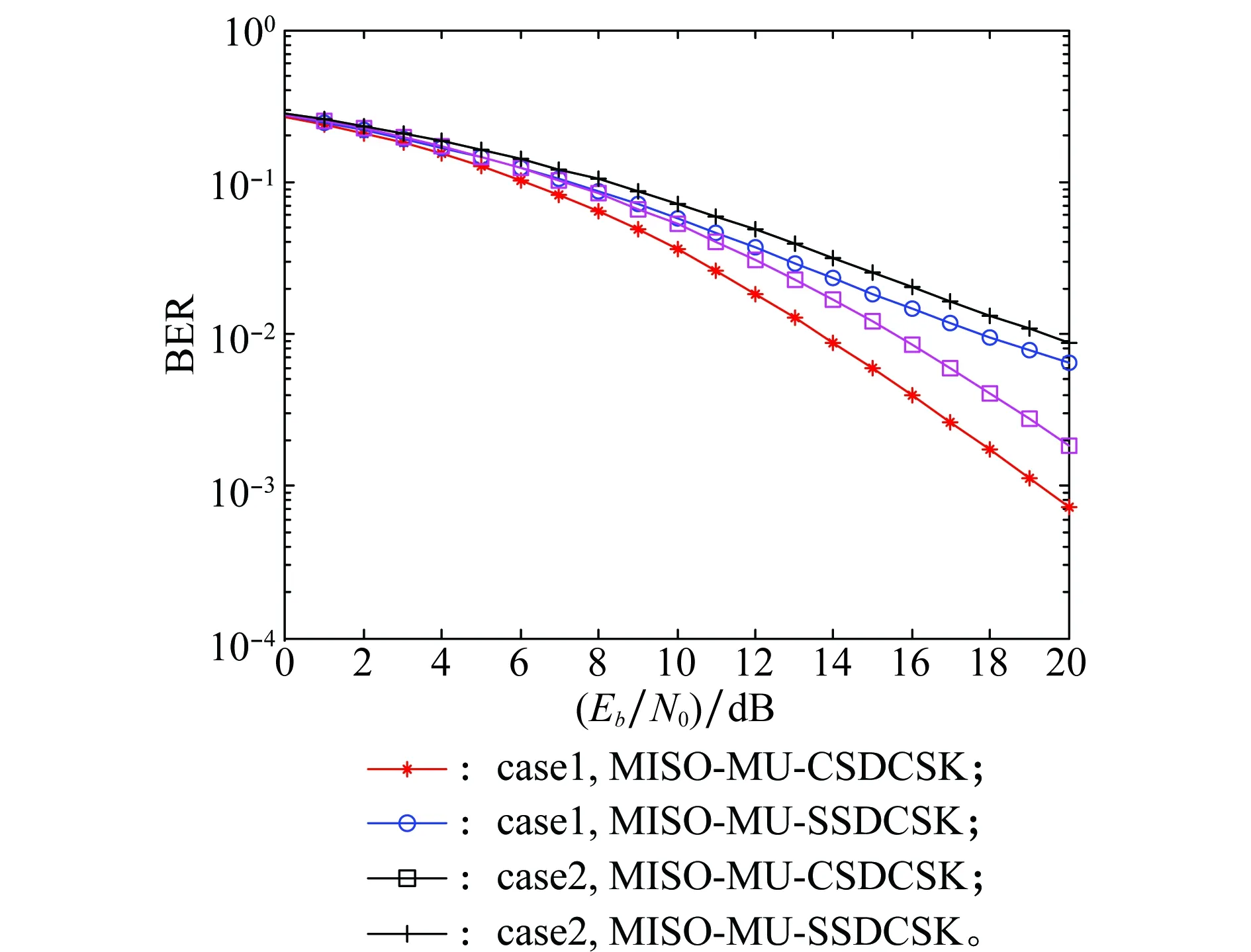
式中,bN(k-1)+n表示为第k帧中第n用户的数据信息且bN(k-1)+n∈{-1,1};1 MU-CSDCSK系统的接收图如图5所示。接收器首先将接收信号ri,k延迟β得到延迟信号ri-β,k,将ri-β,k依次送入各循环移位器得到与相应各用户载波信号相同的信号,然后将ri,k和经过各个循环移位器操作后的信号以及调制时分配给对应用户的Walsh码作相关,最后将相关值送入门限判决器,解调出各用户的传输信息。 MU-SSDCSK系统混沌信号yi,k、归一化混沌信号xi,k、传输信号si,k以及接收信号ri,k的波形图如图6所示。由波形图可以看出混沌信号yi,k的幅度是介于(-1,+1)杂乱无章取值,满足混沌数字通信中对于混沌信号的需求。yi,k经过符号函数映射后产生归一化混沌信号xi,k,从波形图中可以看出xi,k幅度取值只有-1和+1两种情况,所有满足MU-SSDCSK系统对于混沌参考信号的需求。MU-SSDCSK系统的传输信号si,k(假设扩频因子2β=64)前32次迭代中只发送参考信号,所以幅度只有-1和+1两种情况,后32次迭代中发送四用户信息信号,所以其幅值变化范围为(-4,+4),且取值为整数,满足预期效果。接收信号ri,k包括发射信号以及高斯白噪声干扰信号,所以波形图与传输信号存在误差,尤其在前32次迭代过程中,但是这正符合实际通信情况。 图5 MU-CSDCSK系统接收图Fig.5 Receiver block diagram of the MU-CSDCSK 图6 yi,k,xi,k,si,k,ri,k波形图Fig.6 Waveform of yi,k,xi,k,si,k,ri,k (10) 多径Rayleigh衰落信道经常应用于无线通信系统之中,相对于高斯信道更具有现实意义,本文信道模型以两径Rayleigh衰落信道为例进行分析。信道模型如图7所示。 图7 两径Rayleigh衰落信道模型Fig.7 Two-ray Rayleigh quasi-static block faded channel model αl,1和αl,2是满足两径Rayleigh衰落分布的随机变量且相互独立,τ(τ<<2β) 表示两条路径之间的延迟。假设在一个时隙时间内,信道系数保持不变,发送信号经过两径Rayleigh衰落信道后,则接收信号ri,k表达式为 αl,2si,k-τ+ξi (11) 对第k帧第n用户为例进行分析: (12) 在式(12)中 (13) 对式(13)进一步化简为 (14) (15) ξi,kξi-β,kwi,u (16) 式(14)中前两项为有用信号项,后四项为用户干扰项,由于Logistic映射的自相关旁瓣为零以及Walsh码正交特性,所以后四项为零。式(15)和式(16)为噪声干扰项,由于噪声均值为零,根据式(17)可实现信息解调: (17) 通过高斯近似法推导MISO-MU-CSDCSK系统在Rayleigh衰落信道中的误码率公式。并且所有的结果都是基于以下假设条件完成的: (1)ξi为Rayleigh衰落信道中的高斯白噪声,其均值为零,方差为N0/2;对于ξi和ξj,当i≠j时相互独立;并且ξi与混沌信号xi相互独立。即 E{ξiξj}=E{ξi}E{ξj}, var{ξiξj}=var{ξi}var{ξj} E{xiξj}=E{xi}E{ξj}, var{xiξj}=var{xi}var{ξj} (2) 二进制信息{+1,-1}等概率出现。 实际混沌通信中对序列采样点数β的取值一般较大,并根据上述假设条件,式(12)近似服从高斯分布,具体误码率推导公式为 (18) E[B]=E[C]=0 (19) Var(A)=0 (20) (21) (22) 通过式(18)~式(22)可以得到判决变量ZN(k-1)+n的均值和方差为 (23) var[ZN(k-1)+n]=var[A]+var[B]+var[C]+ 2cov[A,B]+2cov[A,C]+2cov[B,C]= (24) 式中,cov[X,Y]代表X与Y的协方差并且cov[A,B]=cov[A,C]=cov[B,C]=0。 由MISO-MU-CSDCSK系统帧结构可以推导出平均比特能量为 (25) MISO-MU-CSDCSK理论误码率公式为 (26) 将式(23)~式(25)代入式(26),则第k帧的第n用户的误码率为 BER= (27) (28) 式中,erfc(·) 为互补误差函数,表示为 (29) (30) γb的概率密度函数为 (31) 考虑到Rayleigh衰落信道对于信号幅度的衰减,根据式(28)和式(31),可以得到MISO-MU-CSDCSK系统误码率为 (32) 不失一般性,对于第k帧其他用户的误码率与式(32)相同。 当αl,1=1且αl,2=0特殊情况下,Rayleigh衰落信道退化为高斯信道,误码率公式可简化为 (33) 当NT=1时,式(33)即为MU-CSDCSK系统的理论误码率公式。当NT=1,N=1时,式(33)即为FM-DCSK系统的理论误码率公式。 由式(28)可知,N、β和γb是影响误码率的重要因素。当混沌序列长度β和γb固定时,存在最佳用户数Nopt使得MISO-MU-CSDCSK系统的误码率最小。首先定义一个函数f(N) (34) 对函数f(N)关于N求导,并且令求导函数为零。 (35) (36) 最佳用户数Nopt为 (37) 由式(37)可知,当β越大γb越小时,对应的最佳用户数Nopt越大;相反最佳用户数Nopt越小。 本小节对MISO-MU-CSDCSK系统在AWGN信道及两径Rayleigh衰落信道中进行了蒙特卡罗仿真分析。图中所有仿真曲线值都是在100 000次仿真结果取平均值前提下得到的。为了表述简单明了,“Theory”表示理论分析,“Sim”表示蒙特卡罗仿真分析。 图8是当天线数NT=2,用户数N=4时,不同混沌序列长度(β=128,256,512)条件下MISO-MU-CSDCSK系统的理论比特误码率仿真曲线和蒙特卡罗仿真曲线对比图。由图8可知,理论曲线与蒙特卡罗仿真曲线完美吻合,证明系统理论推导准确。另一方面,在信噪比Eb/N0一定的情况下,混沌序列长度β越小误码性能越好,证明误码率会随β的增大而恶化。 图8 系统理论误码率和蒙特卡罗仿真比较Fig.8 Comparison of experimental and theoretical values ofMIS0-MU-CSDCSK system 图9是当天线数NT=2,混沌序列长度β=256时,不同用户数(N=2,4,8)条件下MISO-MU-CSDCSK系统误码性能随信噪比变化图。当用户数N固定时,系统误码率随信噪比Eb/N0的增大而逐渐较小。由图9可知,当Eb/N0较小时,N值越大系统误码率越小,当Eb/N0较大时,N值越小系统误码率越小。所以在一定条件下MISO-MU-CSDCSK系统存在最佳用户数使系统的误码率最低。 图9 误码率随信噪比变化曲线Fig.9 Curve of BER with SNR 图10是当天线数NT=2,采样序列β=256时,不同信噪比(Eb/N0=10 dB,12 dB,15 dB)条件下,MISO-MU-CSDCSK系统误码率随用户数N变化趋势图。起初,随着用户数增加系统误码率逐渐降低,但当用户数增大到一定值后,随着用户数的增加系统误码率开始上升。所以在不同信噪比条件下系统存在最佳用户数Nopt。当β=256,Eb/N0为别为10 dB,12 dB和15 dB时,通过图10可以观察到最佳用户数Nopt分别为4,3和3,从而验证了式(37)的准确性。 图10 误码率随用户数变化曲线Fig.10 Curve of BER with the number of users 图11显示的是NT=2,N=4时,不同混沌序列长度(β=128,256,512)条件下MISO-MU-CSDCSK系统与MISO-MU-SSDCSK系统和MISO-VDMA-DCSK系统误码性能对比图。由图11可知,MISO-MU-CSDCSK系统误码性能明显优于MISO-VDMA-DCSK系统。这是由于MISO-MU-CSDCSK系统首先进行了循环移位使用户载波信号各不相同,并通过Walsh码的正交性消除了用户间干扰,大大提高了系统误码性能。与MISO-MU-SSDCSK系统相比,在信噪比Eb/N0较小时,两种系统几乎重合;但是当Eb/N0较大时,MISO-MU-CSDCSK系统误码性能优于MISO-MU-SSDCSK系统,当混沌序列长度β较小时尤为明显,具有优越性。 图11 不同系统性能对比图Fig.11 BER performance comparison of different systems 图12是当N=4,β=256时,不同发射天线(NT=1,2,3)条件下MISO-MU-CSDCSK系统误码性能随信噪比变化图。由图12可知,系统理论误码率与蒙特卡罗仿真曲线吻合,再次证明了系统的可操作性。随着发射天线数的增加系统误码率急速降低,证明增加发射天线数,可以有效地提高系统误码性能。 图12 误码率随天线数变化曲线Fig.12 Curve of BER with the number of antennas 分析MISO-MU-CSDCSK系统在Rayleigh衰落信道下的误码性能,讨论以下两种不同路径增益情况下的系统误码性能。 Case1两条路径具有相同的平均能量增益,即 /2 (38) Case2两条路径的平均能量增益相差10 dB,即 (39) 图13显示的是在Rayleigh衰落信道中当天线数NT=2,用户数N=4时,不同混沌序列长度(β=128,256)条件下MISO-MU-CSDCSK系统理论比特误码率仿真曲线和蒙特卡罗仿真曲线对比图。 图13 Rayleigh衰信道中系统理论误码率和蒙特卡罗仿真比较Fig.13 Comparison of experimental and theoretical values inRayleigh fading channel 从图13可以看出,理论误码率与蒙特卡罗仿真结果基本吻合。在信道增益相同或者不同时,β=256时的误码率总是劣于β=128时的误码率,这是因为β较大时,信道噪声的负面影响越来越严重。图13显示任何β值下,Case1情况下的误码性能总是优于Case2,即等增益优于非增益的情况。 图14显示的是在Rayleigh衰落信道中当天线数NT=2,用户数N=4,β=64时,信道增益相同和不同时,MISO-MU-CSDCSK系统和MISO-MU-SSDCSK系统性能比较图。图14显示,在任意信噪比条件下,MISO-MU-CSDCSK系统的误码性能总是优于MISO-MU-SSDCSK系统,即MISO-MU-CSDCSK系统具有更强的抗信道衰落能力,误码性能更好。 图14 不同信道增益下误码率性能比较Fig.14 Comparison of BER performance in Rayleigh fadingchannel with different gains MU-DCSK技术可以更大程度地提高系统的传输速率,所以具有一定的发展优势。但是传统多用户差分混沌移位键控系统存在码间干扰而造成误码率较高,针对上述问题本文提出了一种基于循环移位的MU-CSDCSK系统。为了更大程度地优化误码性能,将MISO技术应用到MU-CSDCSK系统中,并利用高斯近似法推导了MISO-MU-CSDCSK系统在Rayleigh衰落信道中的误码率公式,通过蒙特卡罗仿真验证了系统的可行性。结果表明:本文所提出的系统能够有效改进多用户差分混沌移位键控系统误码性能较差问题,具有很好的应用价值。 对于MU-DCSK而言,MISO技术的应用可以很好地优化误码性能,但是对于MISO技术与MIMO技术和单输入多输出(signale input multiple output, SIMO)技术的对比应用没有作深入分析。在接下来的研究当中会针对多用户差分混沌移位键控的MIMO技术和SIMO技术作深入研究,将多天线技术与混沌键控技术深入融合。并且针对系统传输安全性问题也需要进行深入分析。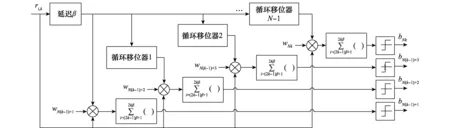
1.3 MISO-MU-CSDCSK通信系统
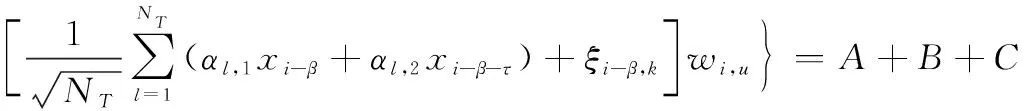

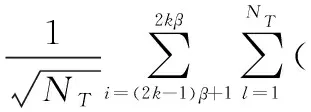
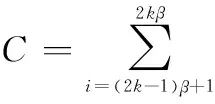
2 MISO-MU-CSDCSK系统性能分析
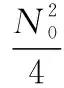
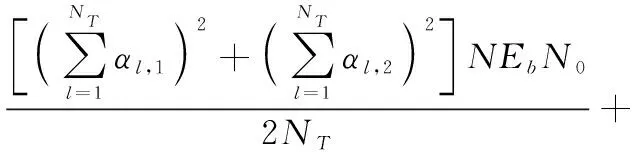
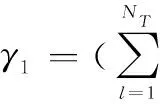
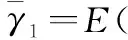
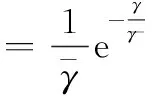

3 仿真分析
3.1 AWGN信道下系统仿真分析
3.2 Rayleigh衰落信道下系统仿真分析

4 结 论
