基于合作博弈的多机飞行冲突解脱策略

蒋旭瑞, 吴明功, 温祥西, 涂从良, 聂党民

(1. 空军工程大学空管领航学院, 陕西 西安 710051; 2. 国家空管防相撞技术重点实验室,陕西 西安 710051; 3. 中国人民解放军94347部队, 辽宁 沈阳 110043)

0 引 言

近年来,我国航空运输需求不断增长,给空中交通管理带来了巨大压力。在现行机场-终端-航路航线的运行模式下,难以突破“人在回路”的制约,空域整体利用率不高。针对这一状况,“自由飞行”[1]是一个有效的解决思路。在自由飞行条件下,飞行员在保证安全间隔的基础上,自主选择航线以提升效率。然而,飞行路线的多向性必然导致飞行冲突的可能性增加。为保证飞机间的安全间隔,寻求一种中、短期飞行冲突解脱方法尤为重要[2]。目前工程上应用最多的冲突解脱方法是几何法,主要采用线性外推的方法预测飞机航迹[3-4]。其主要缺点在于,对于多机冲突解脱的情况,不能保证得到的解是全局最优的。Eby把在机器人领域广泛应用的规避障碍物的方法势能法引入到飞行冲突解脱中[5],势能法具有很强的鲁棒性,能够适应复杂环境,但要求飞机连续大角度机动或速度大范围改变,产生超出边界条件的解。以遗传算法为代表的优化算法是冲突解脱方法中研究较早的智能算法[6-7],遗传算法冲突模型的选择对算法的复杂度有很大的影响,且运算量大。以双机冲突为例,遗传算法运行时间为12.35s,在多机冲突中难以实时解算。

近年来,博弈论在解决冲突、优化资源配置方面的优势被逐渐应用于飞行冲突解脱领域。Tomlin等人使用非合作博弈论研究两机冲突,计算出目标机在最差航迹下我机保持安全间隔的初始状态[8],并在文献[9]中采用微分对策理论证明了密集平行进近阶段邻近两机的可能失误不会违反间隔要求。崔军辉[10]等人使用微分对策理论对感知-规避问题给出了安全区域对无人机飞行策略和制导律的影响。朱衍波使用效益博弈解决双机飞行冲突[11],为博弈论在飞行冲突解脱中的应用提供了指导性思路,但在他的研究中,避让飞机和避让策略的确定是单独的,且支付函数中惩罚与补偿的引入可能剔除满足安全标准的最优解。

基于此,本文针对多机冲突特点,提出了合作博弈飞行冲突解脱模型。以联盟福利最优解均衡各方效益,使可能冲突的飞机各避让较小角度,既保证联盟整体利益,体现公平性要求,又使各机根据重要程度实现了效益均衡。在考察了评价航空器冲突解脱效果的指标后,提出了3种效用函数,分别对应航空器的时间最短策略、避让角度最小策略和综合最优策略。在冲突解脱过程中,首先计算出局中人每一个满足安全间隔标准的可行策略的效用值;其次,对局中人任意策略组合的效用值加权求和得到联盟福利函数;再次,解算出使联盟福利函数最大的策略集合,即为合作博弈的联盟福利最优解;最后,通过粒子群算法求解,降低了运行时间。希望通过以上方法,根据偏好快速获得各方均满意的解脱策略,辅助飞行员决策及管制员调配,实现实时的中、短期冲突解脱。

1 合作博弈与联盟福利最优解

合作博弈是指在协议的约束下各方利益都有所增加,或者在不损害任意一方利益的前提下,有参与者利益增加,从而整个联盟的利益有所增加。与非合作博弈相比,合作博弈更加强调集体主义和团体理性(collective rationality),主要研究了参与者达成合作时如何分配合作所得收益的问题。联盟内部的信息互通和存在有约束力的可执行契约是达成合作博弈的两个前提条件。

合作博弈在发展的过程中提出了众多的解概念,其基本思想就是要设计出一种公平解,促使参与者在不损害联盟利益的前提下获得更高的收益。这里我们以联盟福利最优解[12-13]为解配置均衡各方利益,联盟福利最优解要满足以下3个条件:

(1) 联盟参与人具有为联盟整体谋求最大福利的行为;

(2) 联盟参与人具有追求公平的偏好;

(3) 联盟参与人追求个人利益和公平性不能以牺牲联盟福利为代价。

2 模型的建立与分析

从合作博弈的理论基础中可以发现,多机飞行冲突解脱就是一个多方合作博弈的过程。有冲突风险的航空器是参与博弈的局中人,具有若干飞行解脱策略,它们通过地面、机载通信导航设备实现信息互通,以全国统一的飞行管制为基础形成具有强执行力的稳固联盟,围绕各自的避让支付代价展开合作博弈。一方面,从个体的角度出发,希望自己的避让飞行代价小;而另一方面,从联盟整体角度考虑,要以安全间隔为约束条件并合理均衡各方利益。在航空器重要程度相当的前提下,希望各避让较小角度,避免有的航空器不避让,有的机动角度过大,安全性降低。这种追求整体利益最大化的特点符合联盟福利最优解的特性。

2.1 合作博弈冲突解脱模型

当航空器探测到下一阶段可能发生飞行冲突,各局中人I={i|i∈[1,N]}的所有解脱策略组成策略空间Si(sij∈Si表示参与人i的第j个策略),在安全间隔的约束下互相博弈,获得相应效用u={u1,u2,…,un}。效用函数ui:S→R,表示第i位参与者在不同策略组合下所得的收益。把每个参与者的各一个策略组成的某策略集合{s1,s2,…,sn}对应收益{u1,u2,…,un}加权求和得到联盟福利函数:

·uij

(1)

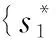
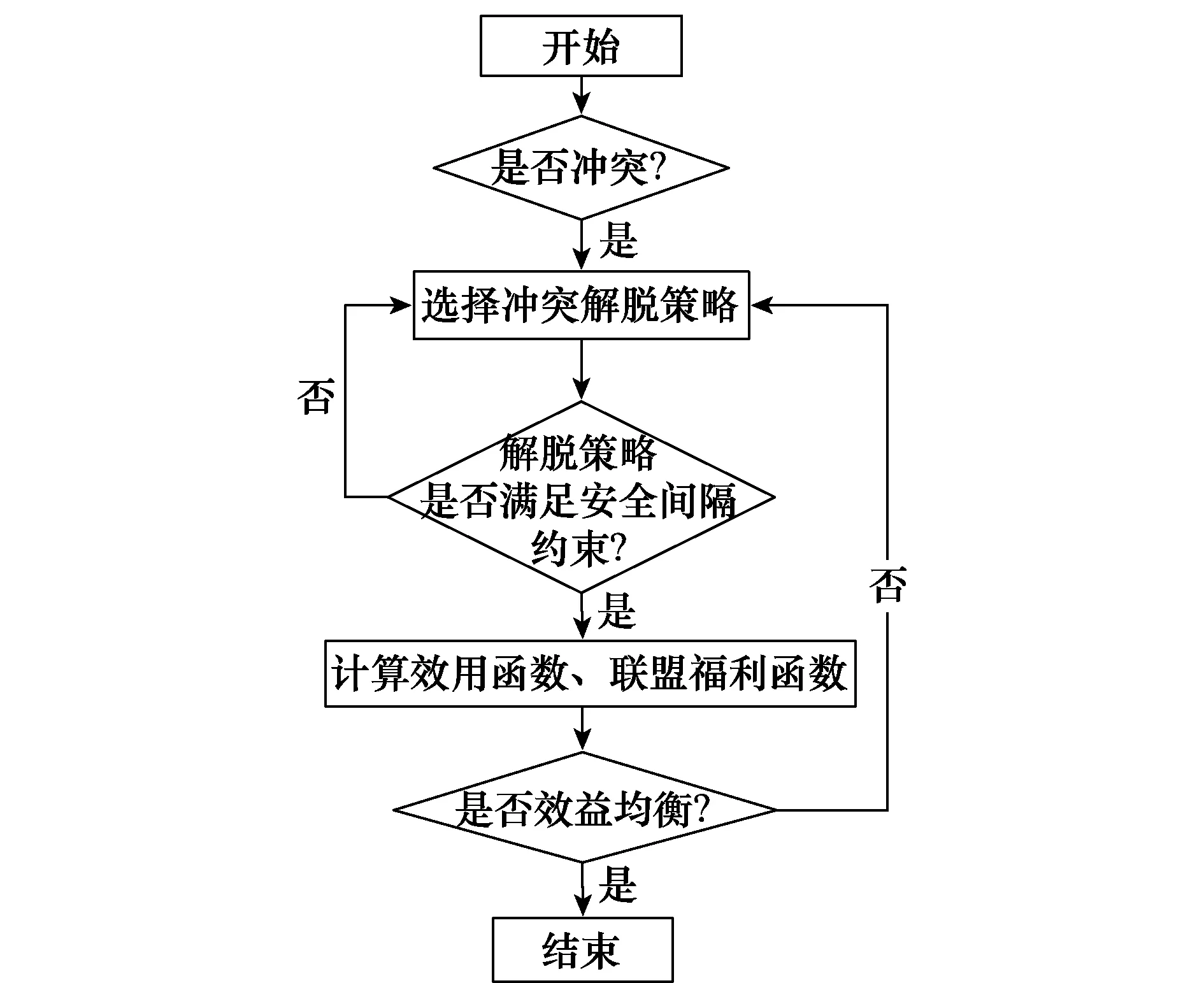
图1 博弈冲突解脱基本流程Fig.1 Flow graph of conflict resolution based on cooperativegame theory

模型中,研究的主要对象是可能发生危险冲突的航空器组成的联盟。参与者之间通过联盟获取更高的效用,而对于某个体航空器而言,所选择的策略不一定是收益最高的。以联盟福利最优解为解配置,在保证航空器联盟安全的前提下,根据付出的总避让代价最小的原则,确定出需要避让的飞机及其机动策略,文中主要研究了航向解脱。

根据飞行操纵的实际情况,将模型简化如下:

(1)在自由飞行条件下,除起飞和降落阶段以外,都是在指定高度层飞行。因此,将模型简化为二维平面的冲突解脱问题。

(2)从安全角度考虑,非战斗机一般不进行大角度机动,我们规定航空器航向角改变范围为[-30°,30°]。在实际飞行中,为方便飞行员操作,管制员一般以整5°指挥飞机航向机动,这里把航向角变化范围也离散成相差5°的策略集合,如图2所示。

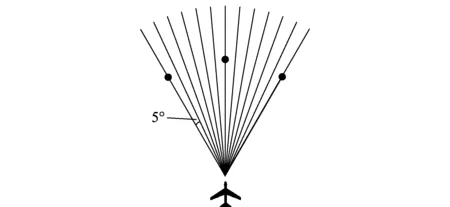
图2 解脱角度离散化Fig.2 Angle discretization

(3)把航空器视为质点,机载雷达探测半径为100 km,在50 km以内建立告警区,10 km以内划设保护区。

当2架飞机进入对方告警区,我们认为存在飞行冲突的潜在威胁,进入解脱流程。为防止当前冲突的双机解脱后与周围飞机发生新的冲突,探测范围内的所有航空器均参与博弈确定避让策略,避免二次解脱。当两机距离小于10 km,我们认为飞行冲突发生,避让失败,即

≤Ssafe

(2)

式中,(xi,yi)和(xj,yj)分别为航空器i、j在平面上的坐标；Ssafe为两机的安全间隔10 km。解脱流程从进入告警区开始,至到达目的地为止。

2.2 效用函数的提出

效用函数又称支付函数,是参与人从博弈中获得的效用水平,主要由避让支付的代价决定。航空器在冲突解脱中支付越少机动成本将获得越高的效用,选择不避让的航空器将获得最高的收益。从航空器整个冲突解脱流程出发,考察各机效益。对于航空器个体而言,在避让中支付的代价,主要由飞行时间、飞行航程(航路费)、航空器耗油量和转弯角度决定。模型假设飞机进入航线飞行后采用巡航速度飞行,且避让时速度大小不变,航程可以表示为时间的函数，即

Stotal=vcruise·ttotal

(3)

式中,Stotal为总航程;vcruise为巡航速度;ttotal为总飞行时间。由于解脱策略仅考虑航向机动,不涉及高度、速度的变化,耗油量可以表示为飞行总时间的函数，即

Q=βttotal

(4)

式中,Q为耗油量;β是燃油消耗率,主要受航空器机型影响。可以看出,影响航空器解脱效用的指标与飞行时间存在密切关系,可以把时间的函数作为博弈中的效用函数,对应的解为时间最优策略，即

(5)

式中,t是该航空器飞行解脱的时间,从进入告警流程开始到解脱结束恢复航线为止。另外,避让的偏转角度也是衡量避让效益的一个重要指标,效用函数对应的解策略为角度最优策略，即

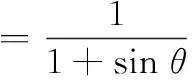
(6)

式中,θ是航空器避让偏转角度,偏转越大,越不利于飞行安全。综合考虑时间和转角的因素,我们提出了时间、角度的综合避让方案,其效用函数可以表示为

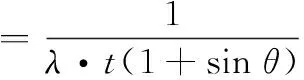
(7)

式中,λ是调节参数，λ越大,表明策略更注重时间指标,反之λ越小,更注重转角指标。

2.3 策略公平性与联盟福利最优的统一性

从第1节中我们知道,如果所得的策略集合单单是公平解,联盟整体福利因为兼顾公平而受到损失,这个解就不是最优的。为了证明联盟福利最优解作为解决飞行冲突解配置的有效性,我们推导了任意航迹交叉角θ下策略公平性与联盟福利的关系。双机对头飞行场景如图3所示。

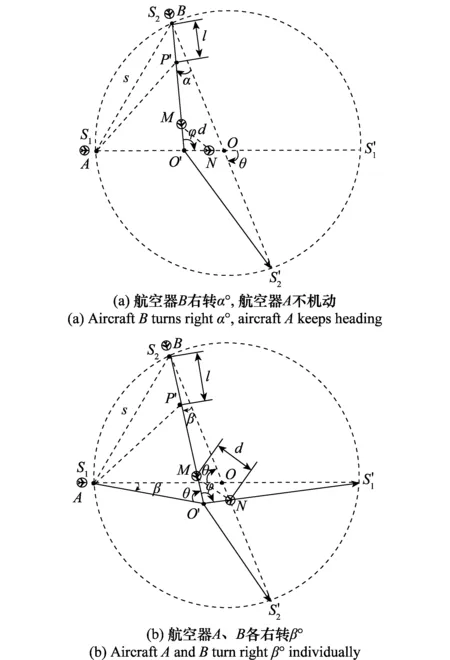
图3 双机汇聚飞行场景 Fig.3 Centering flight of two aircraft

(8)

在ΔS1OS2中,由正弦定理知

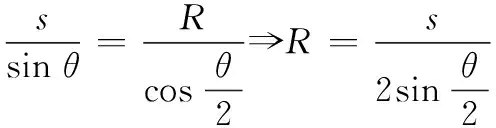
(9)

对于单机解脱的情况,两机距离之和为

(10)

在ΔO′OS2中

φ=π-θ-α

(11)

由正弦定理知

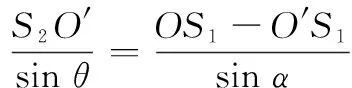
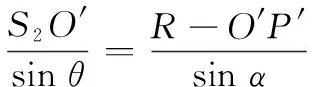
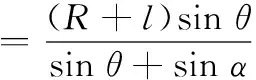
(12)

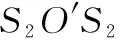
′)2=(S2O′)2+(S2S2′)2-2cosα·S2O′·S2S2′

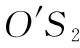
(13)

在ΔS1S2P′中,由正弦定理知

⟺

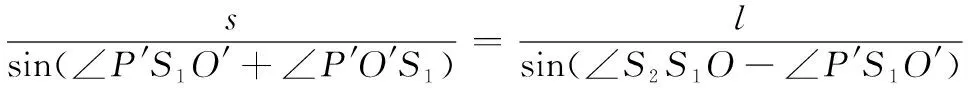
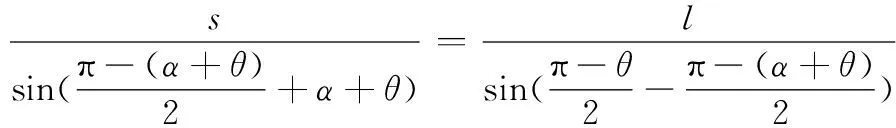
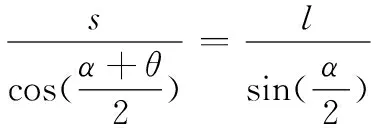
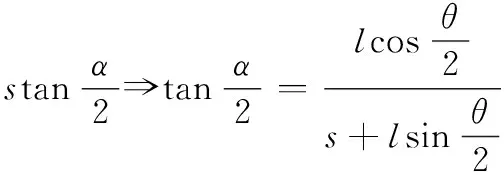
(14)

将式(8)、式(9)、式(11)～式(14)代入式(10)中,可得L1的表达式。

对于双机解脱的情况,两机距离之和为

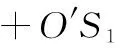
(15)

在ΔS1S2O′中,由正弦定理知

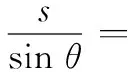
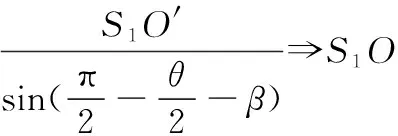
(16)

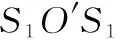
′)2=(S1O′)2+(S1S1′)2-2cosβ·S1O′·S1S1′

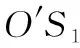
(17)

同理

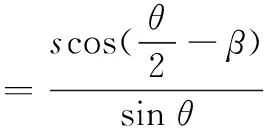
(18)

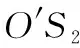
(19)

在ΔS1S2P′中,由正弦定理知

⟺

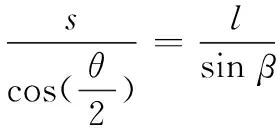
(20)

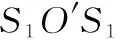
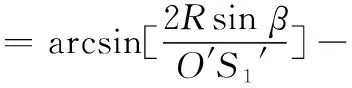
(21)

将式(8)、式(9)、式(16)～式(21)代入式(15)中,可得L2的表达式。令f(θ)=L1-L2,作出L随航迹交叉角θ的变化曲线,如图4所示。

当航向交叉角小于20°时,近似于平行飞行,在冲突解脱问题中,仅通过航向机动调配代价很大,故不作考虑。图4中,函数f(θ)=L1-L2恒大于零,即两机汇聚飞行状态下,无论航向交叉角θ如何变化,单机大角度机动避让较双机同时同角度避让支付代价更大,联盟福利最优解配置的公平性与整体效益性是统一的。另外,航向交叉角越小,双机同时避让的优越性越能体现。

3 基于粒子群优化算法的冲突消解

粒子群优化(particle swarm optimization, PSO)算法是进化算法中的一种用于优化的并行算法。它从随机解出发,经过迭代找出最优解,通过适应度评价解的品质。因其实现容易、精度高、收敛快等特点被广泛应用。

在合作博弈冲突解脱模型中,当冲突机数量较少时(如三机冲突解脱),通过遍历所有航空器的行动集合可以较快地寻优,但当冲突机数量较多时,遍历所有策略组合耗时过长,难以满足实时解脱要求。在六机冲突场景中,遍历13种行动组合共136=4 826 809种情况,仿真运算时间较长。利用粒子群优化算法快速求解,其主要思路如下:

(1)适应度函数

将联盟福利函数作为该问题的适应度函数。

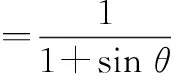
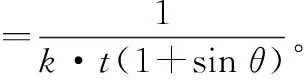
(2)编码方式

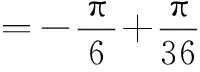
(3)约束条件

①通过取整函数保证运算每一步粒子位置值均为整数;

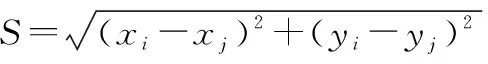
通过不断选择、改变超出边界的位置值保证解的可行性[14]。对于粒子中位置值小于1的情况作如下处理:

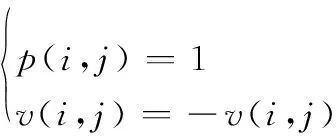
(22)

对粒子位置值大于13的作如下处理:

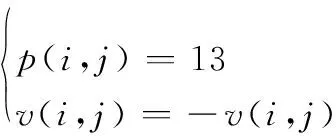
(23)

求解的主要流程如图5所示。

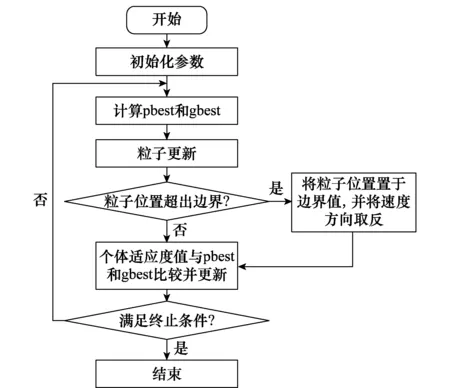
图5 粒子群算法冲突消解主要流程Fig.5 Process of PSO

4 仿真分析

为了验证基于合作博弈的飞行冲突解脱效果,在Matlab环境中分别对三机和六机冲突场景进行了仿真。其中,三机冲突的解算遍历所有策略,根据提出的3种效用函数偏好,得出相应的最优航迹;六机冲突利用粒子群优化算法消解冲突,得出3种策略对应的解脱航迹。以最短时间策略为例,与遍历法求得的航迹进行了比较,从运算时间和适应度两个指标,表明了粒子群算法优化结果的有效性与稳定性。

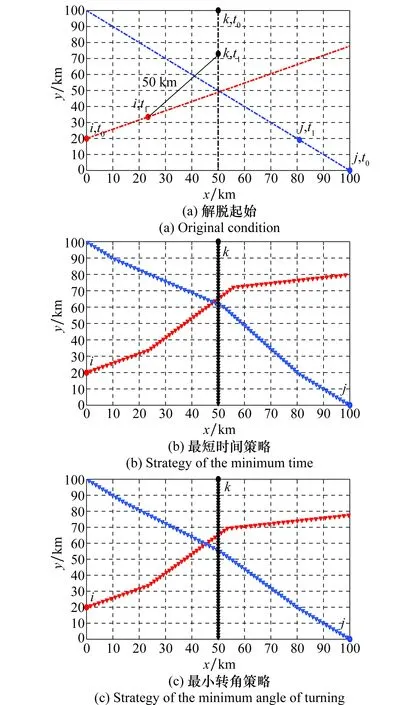
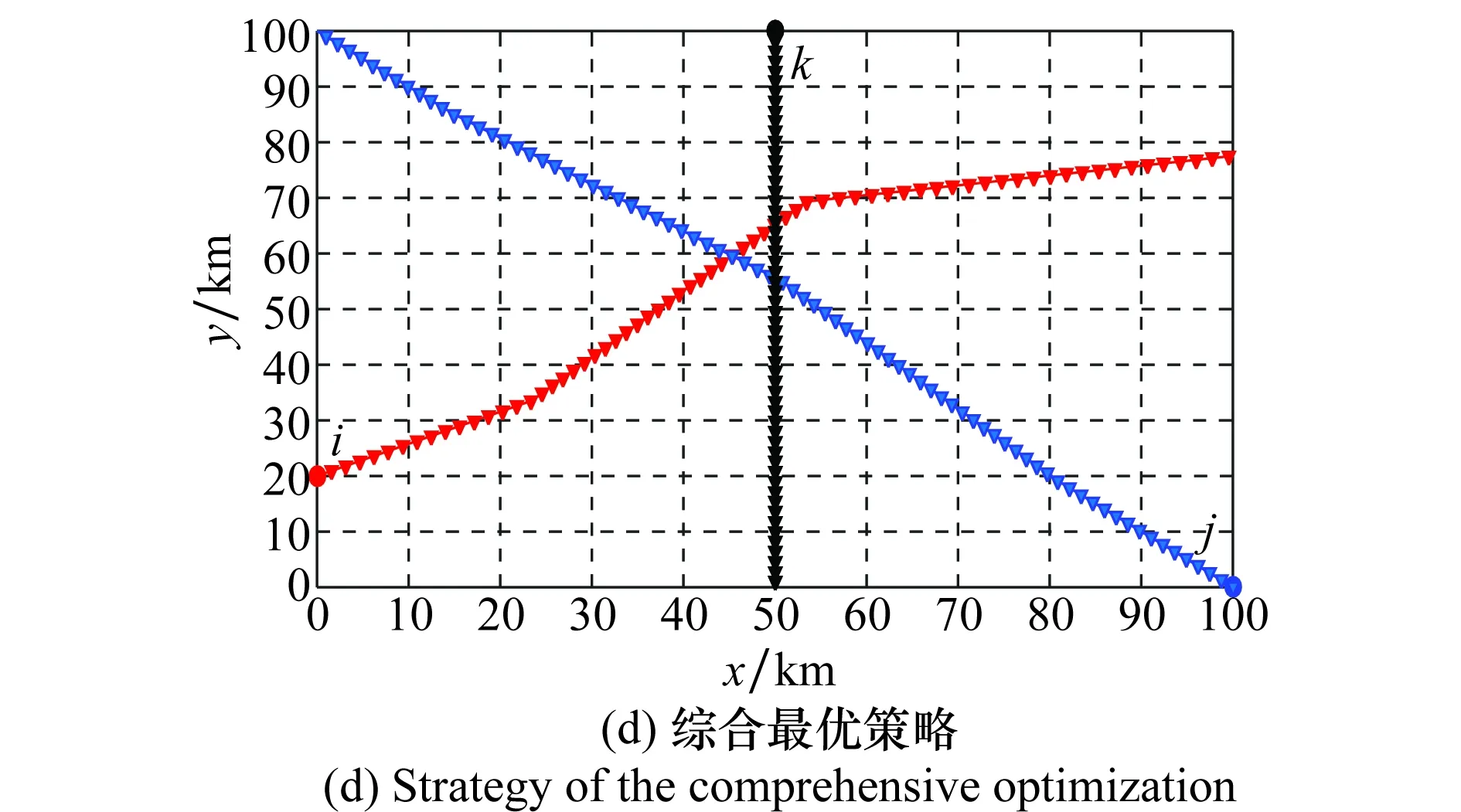
图6 三机冲突解脱轨迹Fig.6 Trajectory of three aircraft resolution

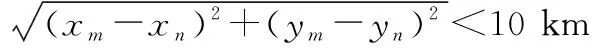
表1 3种策略下航空器机动角度

最小转角和综合最优策略解脱航迹是相同的。从解脱效果看,有效避免了解脱过程中某架航空器采取大角度机动而其他航空器不避让的情况,在均衡效益的同时,实现了联盟利益的最大化。

为了进一步验证模型可行性,针对提出的3种策略,我们对六机冲突场景进行了仿真:a、b、c、d、e、f为6架航空器,在t0时刻分别位于初始位置(20,0),(80,100),(80,0),(20,100),(100,50),(0,50)向目的地飞行,其他参数设置与三机冲突是一致的。

以最短时间策略为例,通过粒子群算法与遍历法求得策略比较,检验了粒子群优化算法的收敛性与稳定性。设置粒子种群数N=20,维度D=6,迭代次数M=50。因满足安全间隔要求的解数量有限,为提高算法跳出局部最优的能力,取较小的学习因子c1=c2=0.8和较大的惯性因子ϖ=0.8。我们考察算法的收敛性,观察策略的适应度值随收敛代数的变化情况,结果如图7所示。

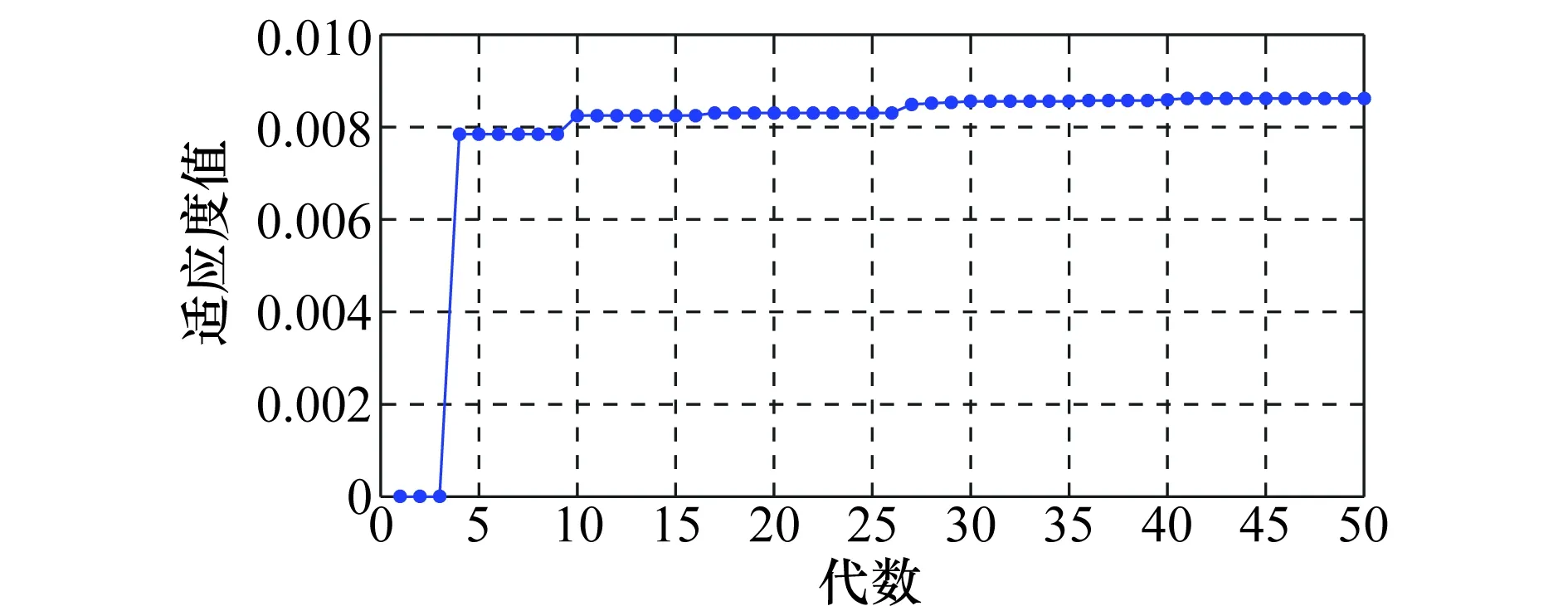
图7 适应度值随收敛代数的变化Fig.7 Change of fitness with the convergence times

从图7中可以看出,算法在第4、10、17、27、36代跳出局部最优,在41代时收敛于全局最优0.008 6,算法收敛性较好。

下面进一步考察算法稳定性,我们对粒子群算法的消解进行了多次仿真,与遍历出的最优策略比较,结果如表2所示。

表2 粒子群优化效果比较

表2首行是遍历法求解的时间最短策略,其余各行是粒子群算法多次运算的结果,以上行动选择均满足安全间隔要求。仿真结果表明,在该参数设置下,粒子群算法多次运行结果适应度值均收敛于0.008 6,与遍历算法求解的联盟福利函数值相等,算法稳定性较好,且运行时间大大缩短。吴君等人的研究中,遗传算法用于两机冲突解脱需12.35 s[15];王渊等人的研究中,改进蜂群算法用于两机冲突需8.22 s[16]。文中提出的合作博弈冲突解脱模型,遍历法用于三机冲突解脱运行时间仅0.36 s,经粒子群算法优化后六机冲突平均运行时间为3.13 s,为实时冲突解脱提供了参考。

利用粒子群优化算法解算最短时间策略、最小转角策略和综合最优策略的解脱航迹如图8所示。

图8 粒子群优化算法消解冲突解脱轨迹Fig.8 Conflict resolution track based on PSO

在这3种偏好解脱策略下,达到均衡点时各机机动角度如表3所示。

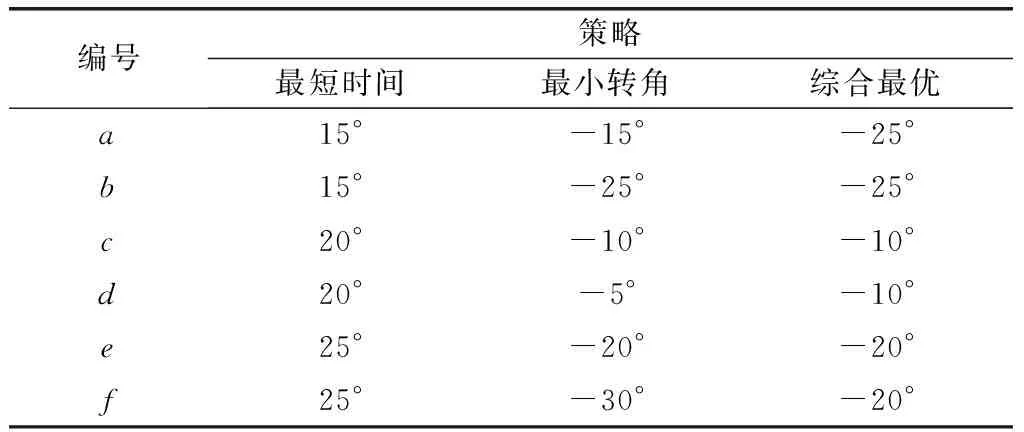
表3 3种策略下航空器机动角度

从仿真结果可以看出,该方法在六机冲突中也能解算出有效的行动选择。我们还可以发现,3种不同效用函数下得出的行动选择均为同向避让,与管制指挥调配规则是一致的。另外,我们还比较了不同策略下各机完成航线飞行的飞行时间,结果如表4所示。

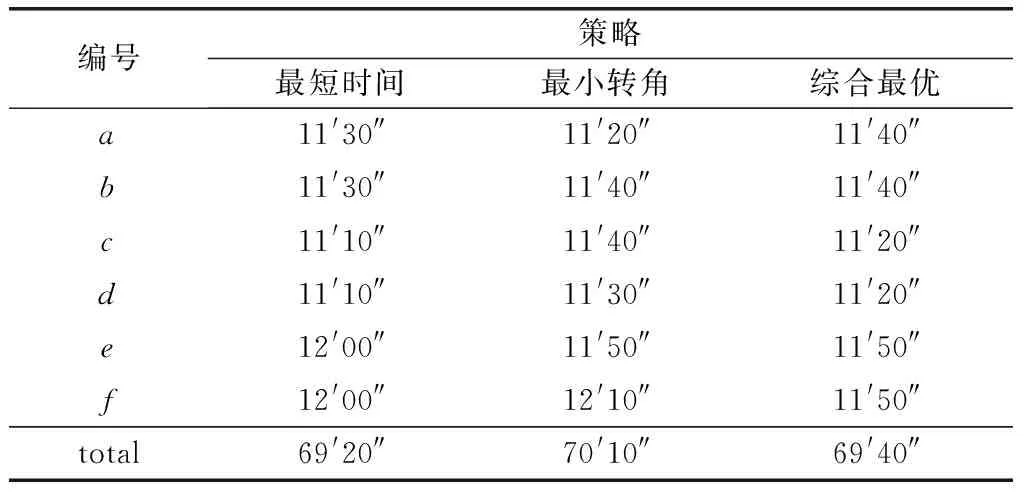
表4 不同策略下各机转角及航线飞行时间

从表4中可以发现,最小转角策略在一定程度上增加了飞行时间,但联盟总机动角度最小,综合最优策略是基于两种策略的一种折中策略,各机的避让时间都在可接受范围内。与遗传算法相比,该算法在将解脱角度离散化处理时,牺牲了部分精度,但以整5°改变航向更加符合飞行实际,且付出的额外时间成本不大。

5 结 论

本文把合作博弈理论应用于飞行冲突解脱领域,提出了合作博弈冲突解脱模型,论证了把联盟福利最优解作为飞行冲突问题解配置的可行性,根据解脱效果的偏好,提出了3种效用函数,在保证飞行联盟整体解脱代价最小的前提下,有效均衡了各方效益,解算出相对公平的解脱行动,并在此基础上通过粒子群算法有效降低了运行时间,实现了实时的冲突探测与解脱。此外,模型可通过调整航空器权重ki,根据飞机的重要程度实现效益均衡;通过调整效用函数中的调节系数λ改变偏好设置,或重新设计效用函数,使解脱策略满足实际的需求。