合成孔径雷达相干与非相干干扰性能分析
2018-11-09杨立波高仕博胡瑞光韦海萍肖利平
杨立波, 高仕博, 胡瑞光, 韦海萍, 肖利平
(1.北京航天自动控制研究所, 北京 100854; 2.宇航智能控制技术国家级重点实验室, 北京 100854)
0 引 言
合成孔径雷达(synthetic aperture radar, SAR)作为高分辨成像雷达,在军事侦察、导弹制导等领域发挥着重要作用[1-10],随着其军事应用的日益广泛和深入,对SAR的干扰技术研究已成为电子对抗领域的重要课题[11-17]。研究分析干扰技术,对SAR及对抗设备研制具有重要意义。
对SAR的干扰包括非相干干扰和相干干扰,通常认为SAR通过二维匹配滤波能够获得很高的处理增益,非相干干扰由于失配于匹配滤波器,干扰功率要求大,而相干干扰能够利用其与雷达信号之间的相干性,提高干扰信号的相关处理增益,可极大降低干扰机辐射功率要求[18-23]。这种观点在形成点目标干扰时是成立的,但是,SAR通常是对大面积场景进行成像,为降低SAR的信息感知能力,电子对抗系统常需形成具有一定距离向和方位向宽度的干扰信号,此时,相干干扰需要将众多点目标信号叠加,而各点目标信号在时域上有很大的重叠范围,这会导致对相干干扰功率需求增大,直观理解,相干干扰不一定具有功率优势。目前尚未见到公开文献对这一问题进行系统性分析。本文采用理论分析和计算机仿真验证的方法,分析了非相干干扰、一维卷积干扰和二维相干干扰的成像前后功率特性,推导了3类干扰的成像处理增益(imaging processing gain,IPG)和干信比(interference-signal power rate, ISR)方程,得出了相干干扰IPG随干扰区面积增大而减小,一定条件下相干干扰与非相干干扰干信比相同的结论。这一结论对SAR及干扰机研制都具有一定指导意义。
1 干扰信号模型及功率特性
1.1 非相干干扰
非相干干扰主要是噪声压制干扰,由于SAR按照脉冲重复频率对信号进行了二维排列,而噪声干扰通常是时间的一维函数,因此,雷达接收到的基带干扰信号可建模为
Jn(tr,ta)=n(tr+ta)
(1)
从后面的分析看出,结论与干扰信号的分布特性和相关特性无关,因此,式(1)中的n(·)为任意的广义平稳随机过程,并设其功率为PJn。由于通过了雷达接收机,n(·)的带宽与雷达带宽相同。
1.2 一维卷积干扰
一维卷积干扰与雷达发射信号相干,设雷达发射信号为
πkr(tr-Ts/2)2}
(2)
式中,rect(·)为单位矩形窗函数;tr为距离向快时间;kr为发射信号线性调频斜率;Ts为发射信号的时宽。
对于SAR,一维卷积干扰可表示为
JR(tr,ta)=h(tr,ta)*s(tr)
(3)
式中,ta为方位向慢时间,h(tr,ta)为短时信号,设其时宽为Th,则
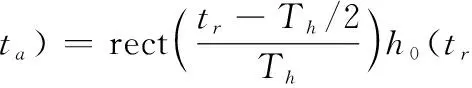
(4)
式中,h0(tr,ta)为平稳随机过程,功率为Ph0,距离向带宽与发射信号带宽相同,设为B,统计特征在各方位时刻相同。
一维卷积干扰信号可理解为h(tr,ta)通过了冲激响应为s(tr)的线性时不变系统,表面上看可采用功率谱密度的方法分析其功率,但由于Th通常不会远大于Ts,系统输出尚未达到稳态,因此,下面采用时域的方法分析其功率。
干扰信号的功率为


(5)
设在带宽B内,h0(tr,ta)在距离向的功率谱密度为常数,则
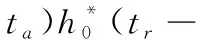
(6)
式中,sinc(·)为辛克函数。将式(6)代入式(5),整理可得


(7)
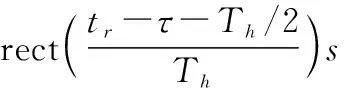


(8)
将式(8)代入式(7),有
(τ′)s(τ′)dτ′
(9)
根据Th与Ts的大小关系,积分后有以下两种结果:
(1) 当Th (10) (2) 当Th≥Ts时 (11) 由于最大功率与干扰机等效辐射功率相对应,下面采用最大功率来表征一维卷积干扰的功率,即 ,Th) (12) 可见,在一定范围内,随着干扰区距离宽度(cTh/2)的增大,距离相干干扰功率也相应增大,当干扰区距离宽度达到SAR成像前距离分辨率(cTs/2)之后,干扰功率不再增大。 二维相干干扰与雷达发射信号和方位向多普勒相位历程都是相干的,忽略距离向和方位向的耦合,二维相干干扰信号可表示[24]为 Jd(tr,ta)=g(tr,ta)*s(tr)*a(ta) (13) 点目标的方位响应函数为 (14) 式中,Ta为合成孔径时间;ka为多普勒调频斜率。 短时信号可表示为 (15) 式中,Tdr、Tda为距离向和方位向时宽,决定了距离向和方位向干扰区域宽度;g0(tr,ta)为二维平稳随机过程,其功率为Pg0。距离向带宽与发射信号带宽相同,方位向带宽与多普勒带宽相同。 采用与一维卷积干扰相同的分析方法,其功率可表示为 s(τr)a(τa)s*(τr′)a*(τa′)}dτrdτadτr′dτa′ (16) 设在距离向带宽和方位向带宽内,g0(tr,ta)的功率谱密度为常数,则 Pg0sinc[(τr′-τr)B]sinc[(τa′-τa)D] (17) 式中,D为多普勒带宽。将式(17)代入式(16),积分可得,二维相干干扰的最大功率为 ,Tdr)min(Ta,Tda) (18) 可见,在一定范围内,随着干扰区面积的增大,二维相干干扰功率也相应增大,但当干扰区方位向宽度大于SAR成像前方位分辨率(vTa),距离向宽度SAR成像距离分辨率(vTs/2)后,干扰功率不再增大。 SAR成像处理过程是两次一维卷积,可表示为 I(tr,ta)=J(tr,ta)*s*(tr)*a*(ta) (19) 式中,J(tr,ta)为接收到的干扰信号;I(tr,ta)为处理后的图像。 非相干干扰的成像处理过程可看作随机过程依次通过两个一维线性时不变系统,系统输出达到稳态后,成像处理后的信号也为平稳随机过程,因此可采用功率谱密度的方法分析其功率。 经过距离向匹配滤波后,输出信号的功率为 (20) 式中,pJn(fr)为干扰信号功率谱密度;|hr(fr)|2为距离向匹配滤波器传递函数绝对值的平方,即 (21) 由于pn(fr)的带宽为B,式(20)积分后可得 (22) 根据式(1)可知,干扰信号在方位向为平稳随机过程经脉冲重复频率的采样信号,其带宽与脉冲重复频率相同,由于脉冲重复间隔远大于干扰信号相关时间,干扰信号在方位向不相关。距离向匹配滤波没有改变干扰信号原来的功率谱密度的形状,滤波后的功率谱密度只是变为了原来Ts/B,相当于通过了一个比例环节。所以,距离向匹配滤波后,干扰信号在方位向的功率谱密度为 (23) 式中,fp为脉冲重复频率。 方位向匹配滤波器传递函数绝对值的平方为 (24) 经方位匹配滤波后,输出信号的功率为 (25) 一维卷积干扰在成像处理后为 IR(tr,ta)=h(tr,ta)*s(tr)*s*(tr)*a*(ta) (26) 式中 s(tr)*s*(tr)=Tssinc(trB) (27) h(tr,ta)虽为距离向的短时信号,但在Th>1/B情况下,h(tr,ta)的带宽不大于B,所以 (28) (29) 干扰信号在方位向为无截断信号,方位向匹配滤波后输出信号也是平稳的,所以,采用与非相干干扰通过方位匹配滤波相同的方法分析其功率,有 (30) 二维相干干扰经成像处理后为 Id(tr,ta)=g(tr,ta)*s(tr)*a(ta)*s*(tr)*a*(ta)= g(tr,ta)*Tssinc(trB)*Tasinc(trD) (31) 在Tdr>1/B、Tda>1/D情况下,g(tr,ta)在距离向的带宽不大于B,在方位向的带宽不大于D,则 (32) 其功率为 (33) 为分析在相同干扰等效辐射功率的情况下,不同模式干扰成像处理后的ISR,定义干扰信号为 (34) 式中,PJ和PI为干扰信号成像处理前后功率;No、Ni为热噪声成像处理前后的功率。 热噪声在成像处理前后的功率比与非相干干扰成像处理前后的功率比相同,有 (35) 所以,非相干干扰的IPG为 IPGn=1 (36) 一维卷积干扰的IPG为 (37) 式中,ρTs为SAR成像前距离分辨率;wh为一维卷积干扰的距离宽度。二维相干干扰的IPG为 (38) 式中,ρTa为SAR成像前方位分辨率,wdr、wda为二维相干干扰的距离宽度和方位长度,fp/D为方位过采样率。 所以,成像处理后的ISR为 (39) 式中,Pt为雷达发射峰值功率;Gt为雷达天线增益;Rt为目标距离;σ为分辨单元的雷达截面积;PjGj为干扰等效功率;kj为干扰功率的失配损失因子;Gθ为雷达在干扰机方向的天线增益;Rj为干扰机到雷达的距离。 将非相干干扰、一维卷积干扰和二维相干干扰的处理增益代入上式,可得出这3类干扰的ISR。 由以上分析可看出,在相同条件下,ISR正比于IPG,一维卷积干扰与非相干干扰的ISR之比等于一维卷积干扰的IPG,二维相干干扰与非相干干扰的ISR之比等于二维相干干扰的IPG。一维卷积干扰的IPG与干扰区距离宽度有关,当干扰区宽度小于SAR成像前距离分辨率时,IPG为SAR成像前距离分辨率与干扰区宽度之比,当干扰区宽度大于或等于SAR成像前距离分辨率时,其IPG为1,不再具有功率优势。二维相干干扰的IPG与干扰区距离宽度和方位长度有关,当干扰区距离宽度和方位长度分别小于SAR成像前距离分辨率和方位分辨率时,其IPG为SAR成像前分辨单元的面积与干扰区面积之比的方位过采样率倍,特别地,点目标干扰时,干扰的距离宽度和方位宽度分别为成像后距离分辨率和方位分辨率,IPG为成像前后分辨单元的面积之比乘以方位过采样率,有 (40) 即为二维处理增益,干扰获得最大处理增益,ISR达到最大。当干扰区距离宽度和方位长度分别大于或等于SAR成像前距离分辨率和方位分辨率时,其IPG为方位过采样率,通常也接近于1,此时其功率优势也不明显。由于在分析过程中,没有约束干扰信号的分布特性,该结论对任意分布都是成立的。 为验证上述分析结果,对3类干扰进行了仿真试验。SAR载频为10 GHz,脉宽为1 μs,带宽为75 MHz,合成孔径时间为0.75 s,多普勒带宽为100 Hz,脉冲重复频率为120 Hz,即方位过采样率为1.2。在仿真中,设置Pt为200 W,Rt为20 km,Gt为37.8 dB,σ为-3 dB,PjGj为500 W,Gθ为15 dB,Rj为18 km,kj为-3 dB,这样根据式(39),非相干干扰的ISR为3.01 dB,并设置了干扰区与SAR成像前距离和方位分辨率的不同比例条件,这样可通过图像、成像后的干扰功率和信号功率分析IPG和ISR。 如图1~图3为成像处理后的图像,其中,图1(a)为无干扰时的成像结果;图1(b)为非相干干扰的成像结果;图2(a)为Th=2Ts时一维卷积干扰成像结果;图2(b)为Th=0.5Ts时一维卷积干扰成像结果;图3(a)为Tdr=2Ts,Tda=2Ta时二维相干干扰成像结果;图3(b)为Tdr=0.5Ts,Tda=0.5Ta时二维相干干扰成像结果。 图1 无干扰和非相干干扰SAR图像Fig.1 SAR image withnot jamming and SAR image withnon-coherent jamming 图2 一维卷积干扰SAR图像Fig.2 SAR image with One dimensional convolution jamming 图3 二维相干干扰SAR图像Fig.3 SAR image with two dimensional coherent jamming 对比图1、图2、图3可看出,在Th=2Ts和Tdr=2Ts,Tda=2Ta条件下,在干扰区域内,一维卷积干扰、二维相干干扰与非相干干扰的效果相当,可获取主要图像特征;对比图2(a)和图2(b),Th=0.5Ts时,在干扰区域内,一维卷积干扰的效果优于Th=2Ts时的干扰效果;对比图3(a)和图3(b),Tdr=0.5Ts,Tda=0.5Ta时,在干扰区域内,二维相干干扰的效果明显优于Tdr=2Ts,Tda=2Ta时的干扰效果。 进行1 000次仿真,统计IPG与ISR均值,结果如表1所示。从表中可看出,仿真得出的结果与理论分析一致。 表1 不同参数下的干扰IPG和ISR 本文从功率角度分析了非相干干扰、一维卷积干扰和二维相干干扰的性能,相干干扰的ISR与干扰区域大小有关,当干扰区域距离宽度比SAR成像前距离分辨率大时,一维卷积干扰较非相干干扰没有功率优势,当干扰区距离宽度和方位长度都大于SAR成像前距离和方位分辨率时,二维相干干扰也没有明显的功率优势。这一结论对SAR及干扰机研制都具有指导意义,对于SAR来说,在保证作用距离的条件下,尽可能采用小脉宽信号,对于SAR干扰机来说,非相干干扰仍是可采用的极为有效的干扰样式。1.3 二维相干干扰


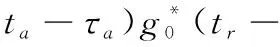
2 干扰信号成像处理后的功率特性
2.1 非相干干扰

2.2 一维卷积干扰


2.3 二维相干干扰

3 干扰信号成像处理增益与干信比

4 3类干扰的仿真分析




5 结束语
