基于凸约束下泰勒估计的主瓣干扰抑制算法

王 伟, 李 壮, 姜 维, 李 欣

(1. 中国电子科技集团公司第二十九研究所, 电子信息控制重点实验室, 四川 成都 610000; 2. 哈尔滨工程大学自动化学院, 黑龙江 哈尔滨 150001)

0 引 言

近年来,自适应波束形成器被广泛应用于无线通信、语音处理、雷达、声纳、医学成像和其他领域[1-3]。传统的自适应波束形成算法如采样矩阵求逆[4-5]、迭代自适应[6-7]、自适应旁瓣对消[8]等,在白噪声环境下,对旁瓣干扰具有很好的干扰抑制效果[9]。当存在主瓣干扰时,利用传统方法进行波束形成,算法会在方向图主瓣内形成零陷造成主波束畸变、旁瓣电平升高等问题,输出信干噪比(signal-to-interference noise ratio, SINR)也会大幅度下降[10]。目前,解决主瓣干扰问题的方法有很多,如文献[11]的大孔径天线阵列,文献[12]的正交极化阵列,上述方法抑制主瓣干扰都是以增加系统复杂度为代价的。文献[13]对阻塞矩阵预处理(blocking matrix preprocess, BMP)类方法进行了总结,包括传统BMP、对角加载BMP以及线性约束BMP。文献[14]改进了阻塞矩阵的构造方法。BMP类算法在已知信号到达角的条件下具有良好的主瓣干扰抑制效果,但存在损失系统自由度和破坏白噪声特性的问题[15]。文献[16]将特征投影矩阵法与干扰噪声协方差矩阵(interference noise covariance matrix,INCM)重构法[17]相结合,解决了传统特征投影预处理(eigen-projection matrix preprocessing, EMP)方法存在的方向图主波束峰值偏移问题。EMP方法由于是在特征空间进行操作,相较于BMP方法鲁棒性更好,且不会造成阵列自由度的损失,但功率较大的主瓣干扰会使得波束形成时旁瓣零陷变浅。文献[18]利用Capon空间谱估计方法构建主瓣干扰信号分量,削弱主瓣干扰对旁瓣零陷的影响。

以上主瓣干扰抑制算法都是基于INCM建立的。EMP方法利用INCM而不是信号协方差矩阵主要出于两点原因,一是在波束形成时避免由于期望信号相消导致的旁瓣电平升高问题;二是防止期望信号的混入导致主瓣干扰对应特征矢量筛选错误。实际中,由于期望信号存在于训练序列中,INCM往往无法直接获得。文献[19]将迭代自适应角度估计与EMP方法相结合,利用迭代自适应法得到的空间谱重构出INCM。但迭代自适应算法[20]精度受网格点数制约,网格点选取越密集,计算量越大。

上述的各种方法都是利用采样协方差矩阵(sampling covariance matrix,SCM)近似代替真实协防差矩阵。当采样信号独立同分布时,SCM为真实协方差矩阵的最大似然估计。然而实际中,采样点数较少或采样信号存在重尾现象,此时SCM将与真实协方差矩阵存在较大误差[21],导致后续波束形成和干扰抑制性能下降。文献[22]对泰勒协方差矩阵估计进行改进[23],提出了泰勒估计加凸约束的协方差矩阵估计方法,该方法计算量低,收敛速度快,在低采样点和低网格点条件下可以得到更为精确的估计协方差矩阵。

受该文献启发,提出了基于凸约束下泰勒估计的主瓣干扰抑制算法。相比于现有方法[24-25],本文方法模拟了实际中采样信号可能出现的低快拍和重尾现象且适用于期望信号存在于训练序列条件。利用估计出的主瓣干扰导向矢量筛选主瓣干扰特征矢量,省去繁琐的INCM重构过程的同时增加了算法鲁棒性。最后,利用线性约束法进行自适应波束形成,避免由于期望信号相消导致方向图畸变、输出SINR降低等问题。仿真结果证明了本文方法具有更稳健波束形成效果和更高的输出SINR。

1 阵列模型

考虑N个阵元组成的均匀线阵,假设阵元间各向同性并忽略阵元间互耦作用,阵元间距为半波长,接收信号模型可表示为

x=Aβ+ε

(1)

式中,A=[a1,a2,…,aL],L为信号个数;β和ε分别代表零均值的信号和噪声;a为信号的导向矢量,可以表示为

a=[ej2πdsin θ/λ,…,ej2π(N-1)dsin θ/λ]

(2)

信号协方差矩阵可以表示为

Σ

(3)

式中,pj为对应信号的方差;Σ=diag(σ1,σ2,…,σN)为NCM。定义P=diag(p1,p2,…，pL),则R可以写作R=APAH+Σ。

传统方法利用SCM近似替代真实协方差矩阵,假设采样点数为K,则SCM可以表示为

(4)

这种做法存在两个缺点,其一,当采样点数较少时协方差矩阵估计精度较低;其二,实际中采样数据往往存在重尾现象或存在异常值,在这种情况下,用该方法估计得到协方差存在较大误差。

2 凸结构约束下的泰勒估计

针对低采样点条件下传统方法SCM估计精度不够的问题,寻找一种高鲁棒性的协方差矩阵估计方法是解决问题的关键。泰勒估计是一种稳健的极值估计方法,表达式为

(5)

s.t.R=APAH

(6)

对任意P>0,代价函数可以表示为

(7)

凸约束下的泰勒估计迭代过程如表1所示。

表1 凸约束下的泰勒估计

表1中,

(8a)

(8b)

(8c)

通过迭代过程可以看出,该方法用对特征值的迭代替代了传统泰勒估计方法对整个协方差矩阵的迭代。这样做大大减少了算法的复杂度,迭代收敛速度更快。

在得到高精度的估计协方差矩阵的基础之上,针对传统EMP方法主瓣干扰特征矢量筛选困难,需要重构INCM,输出SINR较低等问题,本文将空间谱估计与EMP方法相结合,提出了改进抗主瓣干扰自适应波束形成算法。

3 本文算法

EMP方法的难点在于准确的筛选出主瓣干扰对应的特征矢量。传统方法利用特征矢量与期望信号的相关性来筛选主瓣干扰特征矢量,这就要求协方差矩阵中不能含有期望信号,否则会导致特征矢量筛选错误,主瓣干扰无法得到有效抑制。然而,当期望信号存在于训练序列时,INCM无法直接获得,重构INCM的过程计算量较大,且与真实INCM往往存在较大误差,这些都会导致算法干扰抑性能下降。本文方法将空间谱估计与EMP方法相结合,重新定义主瓣干扰对应特征矢量筛选标准,在期望信号存在于训练序列条件下,主瓣干扰抑制以及自适应波束形成性能优异。

(9)

MUSIC空间谱可以表示为

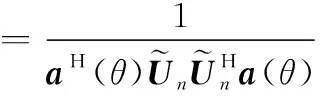
(10)

使θ变化,通过寻找波峰得到各信号的估计到达角。主瓣干扰信号到达角可以通过主瓣宽度进行判别,可得

(11)

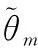
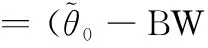
(12)

传统方法通过下式筛选主瓣干扰对应特征矢量um,即

θ0)|2≥c|a(θ0)|2

(13)

式中,c(c>0)是一个依据经验选取的系数,在实际中难以直接获得。文献[16]对传统方法进行了改进,利用相关性筛选主瓣干扰对应特征矢量

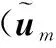
(14)

式中,ρ是相关系数,可以通过式(15)求取

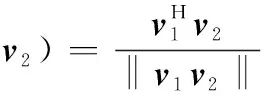
(15)

式中,v1,v2为维度相同的向量;‖·‖表示欧式范数。

当协方差矩阵中存在期望信号分量时,利用上述算法筛选主瓣干扰对应特征矢量,由于期望信号相关度更高,会导致特征矢量筛选错误,造成严重的后果。本文方法由于估计出了主瓣干扰的到达角,通过与估计主瓣干扰导向矢量的相关性判别主瓣干扰特征矢量,在期望信号存在于协方差矩阵条件下,将不会产生特征矢量筛选错误问题。主瓣干扰特征矢量筛选标准可以更新为

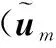
(16)

特征投影矩阵求解公式为

(17)

式中,I为N×N的单位矩阵,阵列输出可以表示为

Y=Bx

(18)

利用最小方差无失真响应(minimum variance distortionless response,MVDR)等方法进行波束形成,由于特征投影矩阵B的存在,波束形成时会产生峰值偏移,输出SINR降低等问题。本文方法由于对信号到达角进行估计,因此可以考虑通过线性约束进行波束形成。为了使得期望信号方向形成最大增益,自适应波束方向图应尽可能的逼近静态方向图。同时还要在旁瓣干扰处形成零陷,达到抑制干扰,提升输出SINR的目的。上述问题可以通过式(19)描述。

(19)

式中,wq为静态权矢量,C是除主瓣干扰信号以外的所有信号导向矢量组成的矩阵,f是列向量,线性约束部分可以表示为

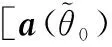
(20)

通过构造拉格朗日函数可以求解自适应权值矢量,即

J(w)=‖w-wq‖2+Re{ηH(CHw-f)}

(21)

式中,η为拉格朗日乘子,令η=2λ,对式(21)求导得到

λ=0

(22)

将式(22)代入式(20)整理得到自适应权矢量为

w=(I-C(CHC)-1CH)wq-C(CHC)-1f

(23)

最后,阵列输出可以表示为

Z=wHY=wHBx

(24)

本文提出的算法流程如图1所示。

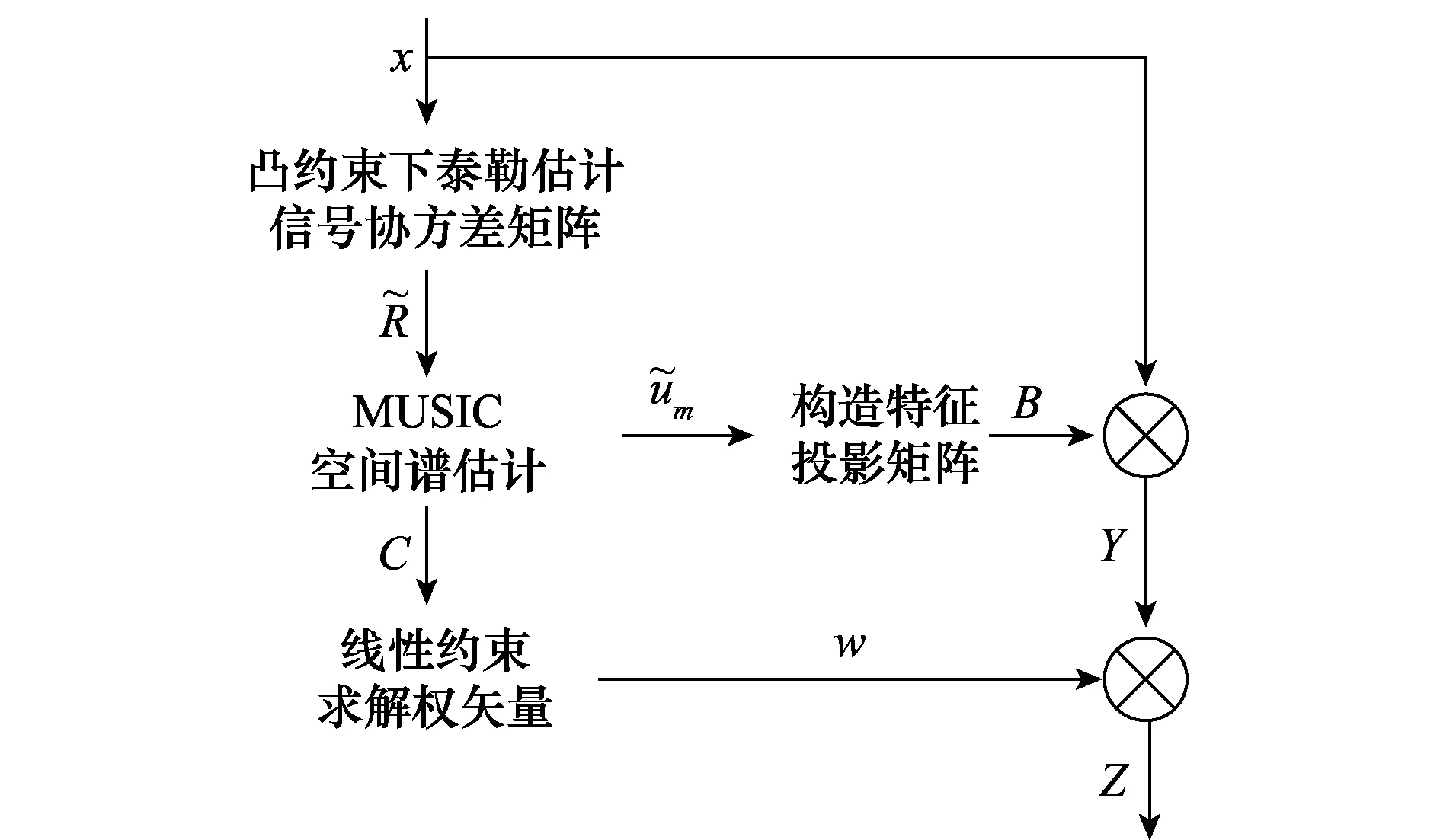
图1 本文所提算法流程框图Fig.1 Processing block diagram of the proposed algorithm

对比文献[19]中算法流程,可以看出,本文算法更为简洁,省去了多次对INCM进行重构的过程,算法复杂度大大降低。利用凸约束下的泰勒估计对信号协方差矩阵进行估计,使得估计出的协方差矩阵非常接近真实协方差矩阵,为低采样点条件下提高波达方向(direction of arrival, DOA)估计精度和谱峰检测概率奠定了基础。利用MUSIC算法进行空间谱估计,并利用估计出的主瓣干扰导向矢量筛选主瓣干扰对应特征矢量,在期望信号存在于训练序列条件下提升了算法的鲁棒性。利用线性约束求解自适应权矢量,解决了期望信号存在于训练序列条件下,MVDR等传统自适应波束形成算法由于期望信号相消造成的方向图畸变问题。

4 仿真实验与分析

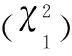
(25)

实验1信号协方差矩阵估计误差

信号协方差矩阵的估计误差会对特征子空间类的算法产生较大影响。传统算法利用采样协方差矩阵近似替代真实协方差矩阵,对协方差矩阵的估计误差很少深入分析。事实上,在采样点数较小或采样信号存在重尾现象的条件下,采样协方差矩阵的估计误差很大,导致后续算法性能严重下降。本实验利用标准均方误差(normalized mean square error, NMSE)来评估协方差矩阵的估计误差,即

(26)

每一组数据都由100次蒙特卡罗实验取平均值,信号数=5,阵元数=16,仿真结果如图2所示。本实验对比了3种协方差矩阵估计方法,传统SCM法,泰勒估计法和本文采用的凸约束下的泰勒估计法。

图2 信号协方差矩阵估计误差Fig.2 Estimation error of the SCM

通过观察图2仿真结果可以看出,随着采样点数的增加,3种方法的估计精度都有所提高。低采样点数条件下,SCM估计存在较大误差,而本文所采用的凸约束泰勒估计方法估计精度高,且采样点数变化对估计精度影响较小。

实验2MUSIC空间谱及估计误差

主瓣干扰由于空间位置上与期望信号相近,且功率较大,在采样点数较低的情况下,利用SCM进行空间谱估计会存在谱峰偏移,谱峰消失等问题。本文仿真了3种信号协方差矩阵估计方法下MUSIC空间谱估计的性能,同时对估计误差进行了研究。MUSIC算法的估计误差可以通过噪声子空间的估计误差来反映,定义估计误差为

(27)

图3是采样点数N=20的条件下,3种方法MUSIC估计出的空间谱。

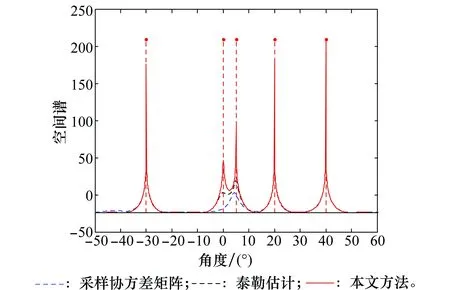
图3 MUSIC DOA估计(N=20)Fig.3 DOA estimated by MUSIC (N=20)

通过仿真图可以看出,传统采样协方差矩阵在低快拍条件无法分辨出期望信号和主瓣干扰信号。而本文所采用的方法谱峰清晰无偏移,通过谱峰搜索可以得到准确的DOA估计值。图4为噪声子空间估计误差随采样点数变化的曲线,蒙特卡罗实验数为100。

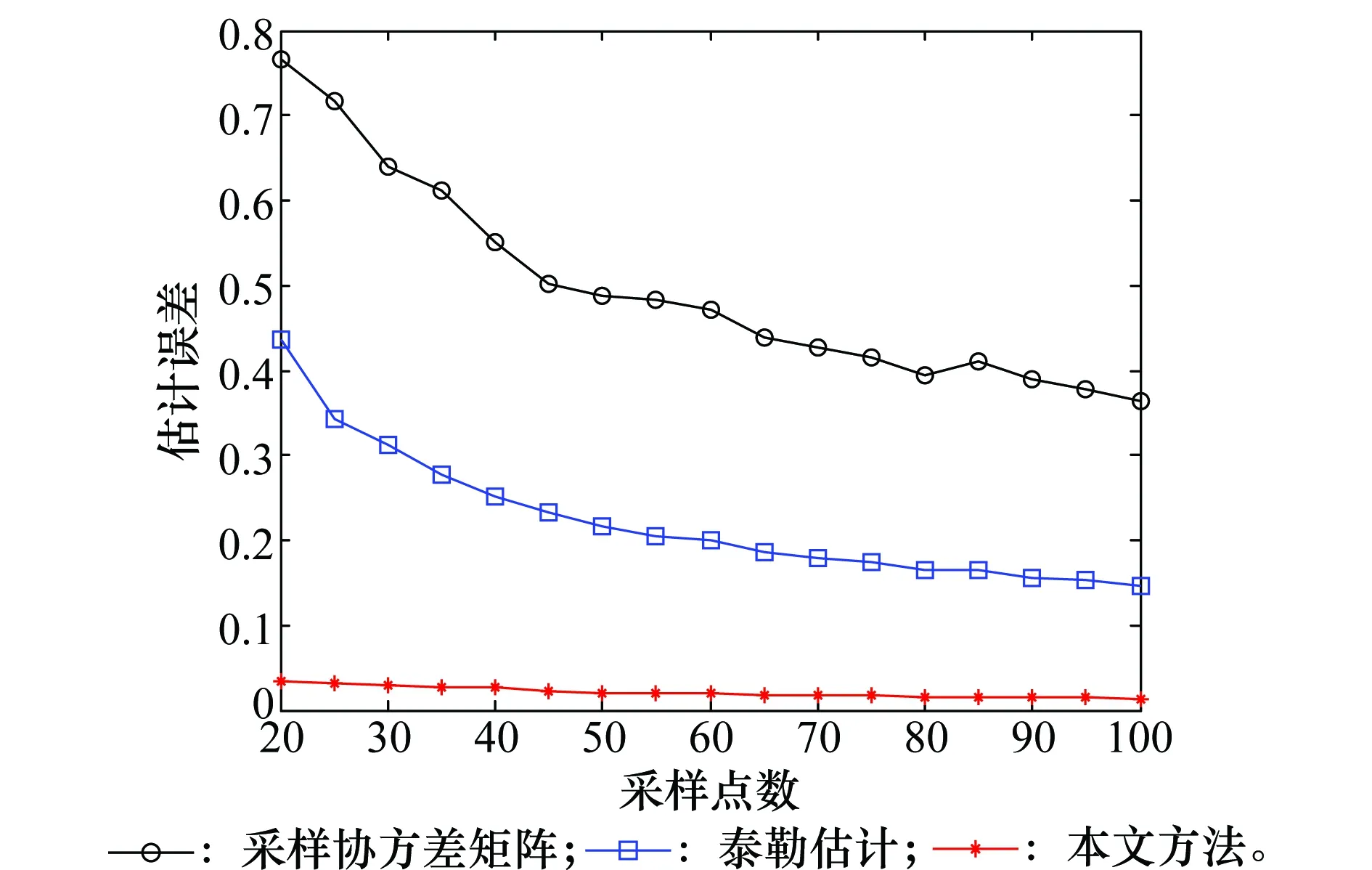
图4 噪声子空间估计误差Fig.4 Estimation error of noise subspace

通过曲线可以看出,本文方法对噪声子空间估计精度较高,且性能受采样点数影响较小。

实验3波束形成方向图

图5给出了本文方法、传统EMP方法、文献[16]提出的协方差矩阵重构EMP方法的波束形成方向图,采样点数为20。

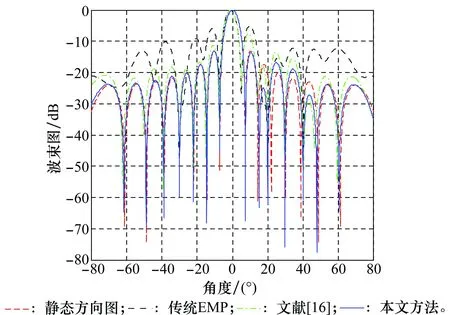
图5 自适应阵列方向图Fig.5 Beam pattern of adaptive array

通过仿真图形可以看出,由于期望信号存在于训练序列中,且受到特征投影矩阵B的影响,传统EMP方法波形畸变严重。在低采样点条件下,协方差矩阵估计精度较低导致协方差矩阵重构EMP方法也出现了旁瓣电平升高以及主波束峰值轻微偏移的问题。本文方法利用线性约束进行波束形成,在低采样点数和期望信号混入训练序列条件下仍具有良好的波束形成效果。波束形成方向图在期望信号方向形成主瓣,主波束无畸变和偏移问题,旁瓣电平逼近静态方向图水平,同时在旁瓣干扰位置能够准确的形成-60～-70 dB的深零陷,相较于现有算法,本文方法具有明显的性能优势。

实验4输出SINR

图6是训练序列中存在期望信号条件下几种算法输出SINR随采样点数变化的曲线。蒙特卡罗实验数为100。

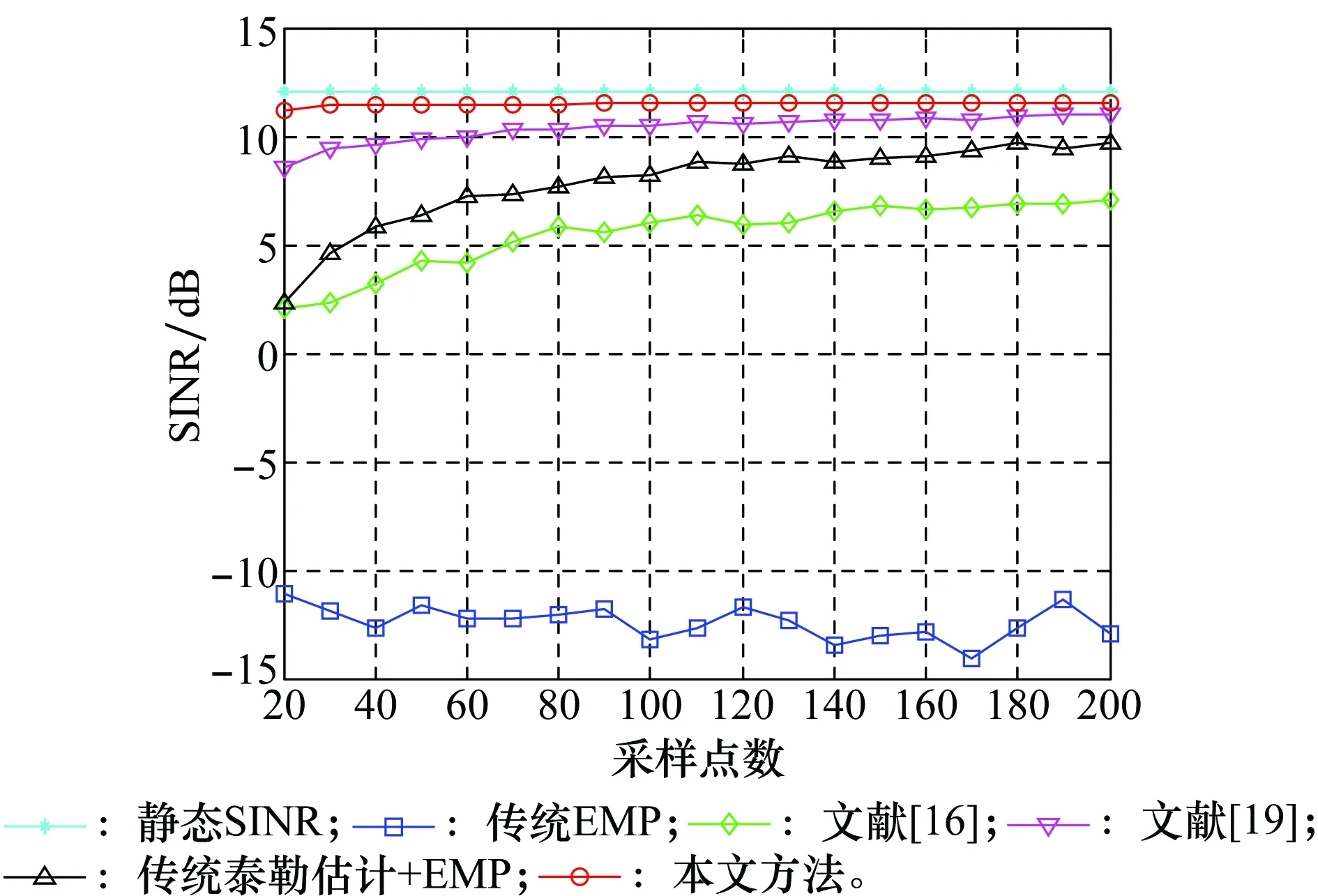
图6 输出SINR随快拍数变化Fig.6 Output SINR versus the number of snapshots

分析仿真图形,由于期望信号的存在以及特征投影矩阵B的影响,传统EMP方法输出SINR非常低,进行协方差矩阵重构后(文献[16])输出SINR有明显改善,但期望信号相消仍然使得输出SINR有所下降。文献[19]方法由于利用迭代自适应法重构了INCM,解决了波束形成时期望信号相消的问题,在采样点数较高的条件下输出SINR与本文方法相近,但在低采样点条件下,本文算法仍具有明显优势。相较于泰勒估计方法,本文所采用的凸约束下泰勒估计法对信号协方差矩阵估计精度更高,对主瓣干扰抑制更加彻底,从仿真图中可以看出,本文方法输出SINR接近静态输出水平。

实验5均匀面阵仿真

上述实验对本文所提出方法的估计误差,干扰抑制性能等进行了详细的分析,实验5将通过仿真验证算法拓展到二维阵列的有效性。实验采用10×10的均匀面阵,坐标系建立参考文献[27],阵元间距为半波长,期望信号SNR为0 dB,来波方向为俯仰0°,方位0°;主瓣干扰SINR为10 dB,方向为俯仰5°,方位5°;旁瓣干扰SINR为20 dB,方向为俯仰45°,方位-30°。图7为采样点数为20的条件下,MUSIC估计出的空间谱。

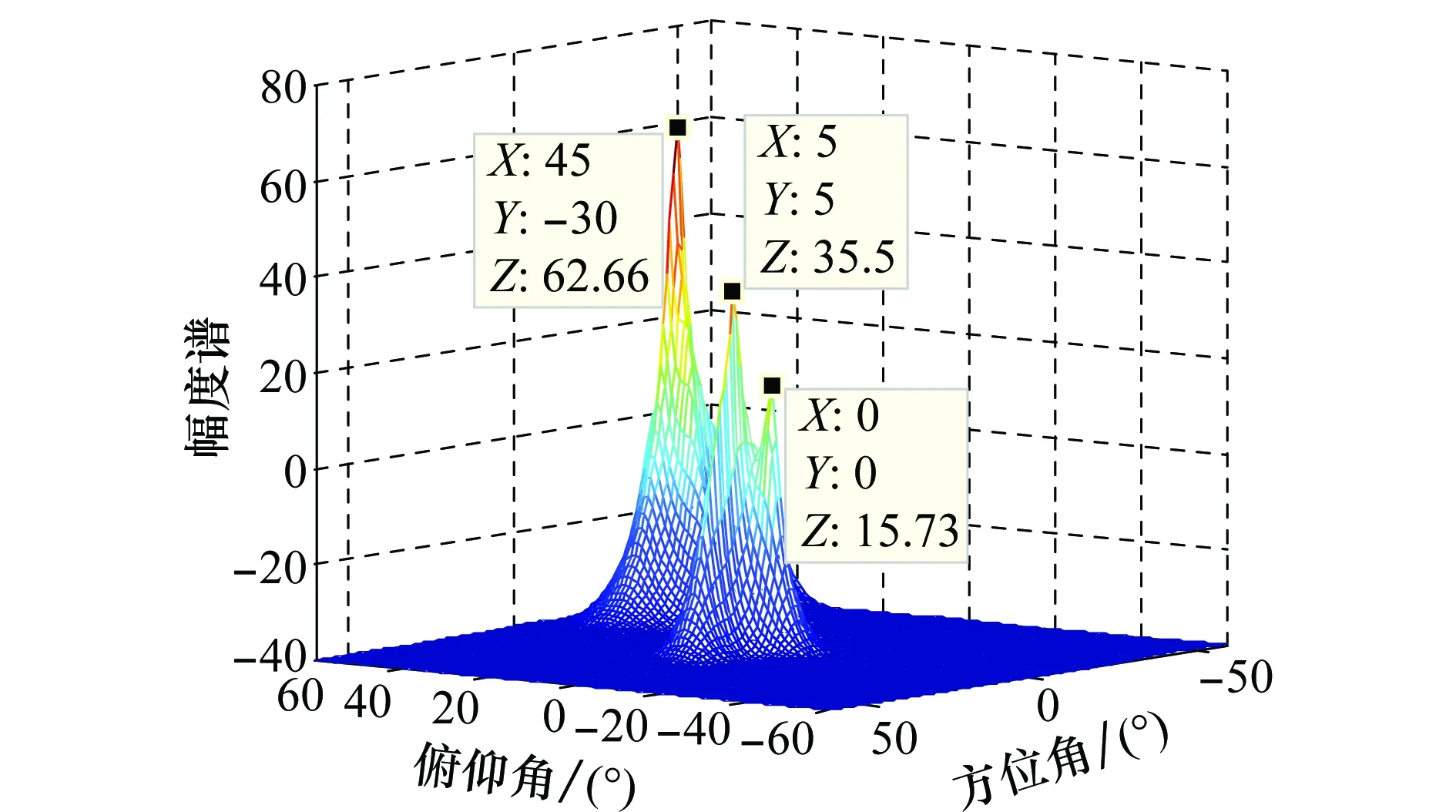
图7 均匀面阵MUSIC空间谱Fig.7 MUSIC space spectrum of uniform plane array

通过仿真图可以看出,本文算法应用于二维阵列在低采样点条件下可以清晰的分辨出空间分布较近的期望信号与主瓣干扰信号。图8为主瓣干扰抑制后的波束形成方向图。

图8 均匀面阵方向图Fig.8 Beam pattern of uniform plane array

通过仿真图可以看出,由于主瓣干扰被消除,方向图主波束无畸变和峰值偏移的问题,在旁瓣干扰位置能够准确的形成零陷,可以对旁瓣干扰进行有效抑制。

5 结 论

提出了基于凸约束下泰勒估计的抗主瓣干扰自适应波束形成方法。本文方法适用于训练序列存在期望信号和低采样点条件。相比现有EMP类主瓣干扰抑制算法,本文方法省去了繁琐的重构INCM的过程,方法复杂度更低。利用线性约束进行自适应波束形成,能够在期望信号方向形成主瓣,旁瓣干扰位置准确的形成深零陷,同时能够获得较低的旁瓣增益,避免了期望信号相消引起的波形畸变和输出SINR降低问题。理论分析和仿真结果显示,本文方法输出SINR明显高于其他对比算法,说明该算法对主、旁瓣干扰抑制更加充分,算法性能优越。