约束条件下两个Pareto总体的参数估计

(吉林师范大学博达学院，吉林 四平 136000)

0 引 言

近年来，随着统计学的发展，对序约束下多个总体参数估计的研究已有很大发展.目前对k个有序正态均值的极大似然估计(MLE)、多个指数总体参数的极大似然估计、二项分布的混合估计以及最小最大估计、可容许估计等方面的问题已经有了明确的研究成果.但现有研究均未考虑约束条件下两个Pareto总体的参数估计问题.

1 半序约束下两个Pareto总体参数的Bayes估计

设X11,X12,...,X1n1和X21,X22,...,X2n2是分别来自于参数为(b1,θ1)和(b2,θ2)的Pareto总体的样本，并且彼此独立.这里，Pareto总体的密度函数为：

p(x|θi)=θibiθix-(θi+1),x>bi>0,θi>0(i=1,2)如果根据实际问题所提供的知识，有

θ1θ2

(1)

要根据以上样本，求(1.1)式成立时，(θ1,θ2)的Bayes估计.

1.1 先验分布的选取

根据文献[1]，如果单样本总体的先验分布选取参数为(a,b)的Gamma分布时，(θ1,θ2)在约束条件(1.1)下的先验分布为：

并且在平方损失下，后验期望向量(E(θ1|X),E(θ2|X))为(θ1,θ2)的Bayes估计.其中X=(X11,...,X1n1,X21,...,X2n2)

1.2 后验密度

设Xij服从Pareto 分布，j= 1,2,...,ni，i=1,2，Xij相互独立.假定根据某些已知信息，有(1)式成立，则由因子分解定理及充分性原则，即可通过

来求(θ1,θ2)的Bayes估计，即(θ1,θ2)的Bayes估计为(E(θ1|T1,T2),E(θ2|T1,T2))，为此，先计算后验密度.

引理1.2.1[3]X～Pareto(b,θ)，则lnX～Exp(lnb,θ),进而有

θ(lnT-lnb)～Exp(1)=Ga(1,1)

引理1.2.2X1,X2,...,Xn是来自Pareto(b,θ)的简单样本，则

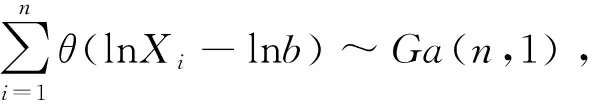
命题1.2 在约束条件(1)下，当单样本总体的先验分布为Gamma分布时，Pareto分布的

后验密度为：

证明： 由引理1.2.2，(T1,T2)关于(θ1,θ2)的条件密度为

于是，(T1,T2)的边际密度

即

化简整理得：

m(t1,t2)=

∵

(2)

∴m(t1,t2)=

∴后验密度

=

1.3 Bayes估计

命题1.3 在约束条件(1)下，当单样本总体的先验分布为Gamma分布时，两个Pareto总体参数的Bayes估计为：

E(θ1|T1,T2)=

证明：

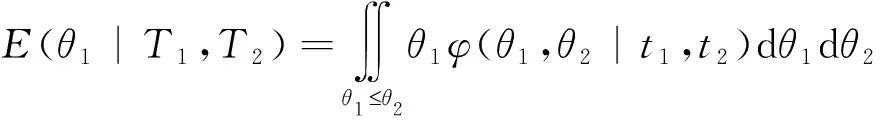
由(2)式，

同理

2 锥序约束下两个Pareto总体参数的极大似然估计

2.1 单样本Pareto总体参数的极大似然估计

引理2.1 设X～Pareto(x|b,θ)，抽取样本X1,X2,...,Xn，则θ的极大似然估计为

证明： 对于样本X1,X2,...,Xn，似然函数

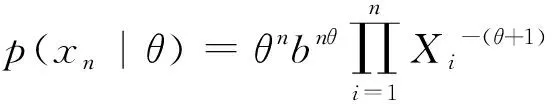
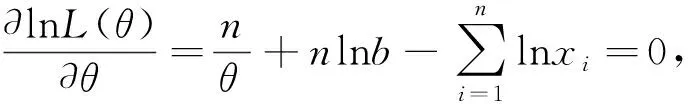
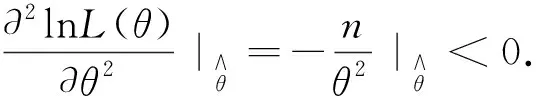
2.2 两个Pareto总体参数的约束极大似然估计问题

设X11,X12,...,X1n1和X21,X22,...,X2n2是分别来自于参数为(b1,θ1)和(b2,θ2)的Pareto总体的样本，并且彼此独立.这里，Pareto分布的密度函数为：

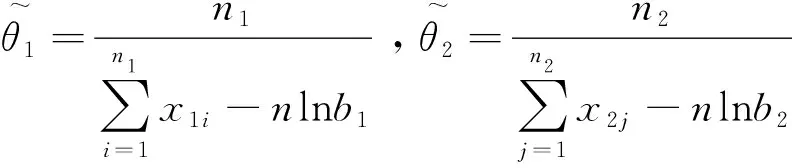
此时样本X11,X12,...,X1n1,X21,X22,...,X2n2的似然函数

因此，对数似然函数为

lnL(θ1,θ2)=n1lnθ1+n2lnθ2+n1θ1lnb1+

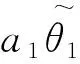
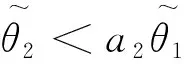
{(θ1,θ2):θ2=a1θ1}上的点，这相当于在约束θ2=a1θ1下，求Laglange函数

的最大值点，即约束极大似然估计.由Laglange乘子法可得

解之可得θ1,θ2的极大似然估计分别为

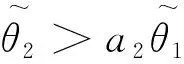
G(θ1,θ2,a)=n1lnθ1+n2lnθ2+n1θ1lnb1+n2θ2lnb2-

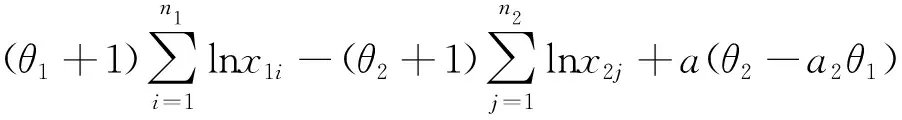
的最大值点，同样解得θ1，θ2的约束极大似然估计分别为：

3 结 语

在半序约束下，当先验分布为Gamma分布时，计算了Pareto总体参数的后验密度，并给出了两个Pareto总体参数的Bayes估计；在锥序约束下，根据Laglange乘子法，计算了两个Pareto总体参数的极大似然估计.