基于排名的变量型主成分分析法在学生综合成绩评价中的应用
2018-11-09,
,
(佳木斯大学 理学院,黑龙江 佳木斯 154007)
0 引 言
学生的综合素质的培养是国家未来人才培养的重要基础,学生的课程学习成绩是学生综合素质的一个最直观的反映,也是学校教学效果的重要反映。通过对课程成绩进行综合评价和排名,同时不但能够了解学生的学习成绩所处的层次,而且是教育管理工作中各种评教重要依据,是教育教学效果评价的重要内容。
综合评价方法大体分两类,不同之处主要体现在指标体系的权重确定方法上。一种方式是主观赋权法,如综合指数法,层次分析法、专家评审法等。其中层次分析法在学生成绩的综合评价中应用较多。另一种方式是客观赋权法,如主成分分析法,因子分析法,灰色关联法等。近几年来,主成分分析法常常用于成绩的综合评价上,均方差法主要用来确定评价指标体的权重[5],秩和比综合评价法主要用于医疗卫生等领域当中的多指标评价问题[6]。
在对学生成绩评价时,各科总成绩的高低仍然是目前所采用的主要因素。基于原始数据,利用变量型主成分分析法探索各指标的权重,并从学生成绩排名的角度出发,重新探究学生的综合成绩,希望对学生的能力有一个更加全面的评价。
1 相关原理介绍
1.1 主成分综合评价法

1.2 基于变量的主成分分析法
对于同样的n名学生,p门课程,这里用X1,X2,…,Xp表示样本观测值即不同学生各门课程的成绩,也就是说,此时的n名学生作为评价指标,而各门课程作为样本。首先,利用主成分分析法,根据累积贡献率确定主成分的个数。其次,对主成分的内在含义进行适当的分析。接下来,计算各个样本(课程)的主成分得分,分数的高低反映了各门课程的重要性程度,然后对主成分得分进行数据转换,将其转换为各门课程的权重。最后,在各门课程权重的基础上,重新计算学生的综合成绩,并与原始成绩进行统计比较。
2 模型建立与求解
2.1 基于排名的主成分分析法
数据来源为某中学学生成绩,课程门数9门,学生人数1383人,部分数据见表1:

表1 学生成绩部分数据
基于排名的主成分分析法具体算法步骤如下:

图1 原始成绩与主成分综合成绩的回归关系
(i)数据的导入与标准化
(ii)根据标准化数据表计算相关系数矩阵,并求出对应的特征值和特征向量;
(iii)计算累积贡献率,选取主成分;
(iv)将标准化原始数据带入,计算学生成绩排名的主成分综合得分;
(v)根据得分进行排序并与原始排名进行比较。
应用Spss结合MATLAB软件得到结果见表2。
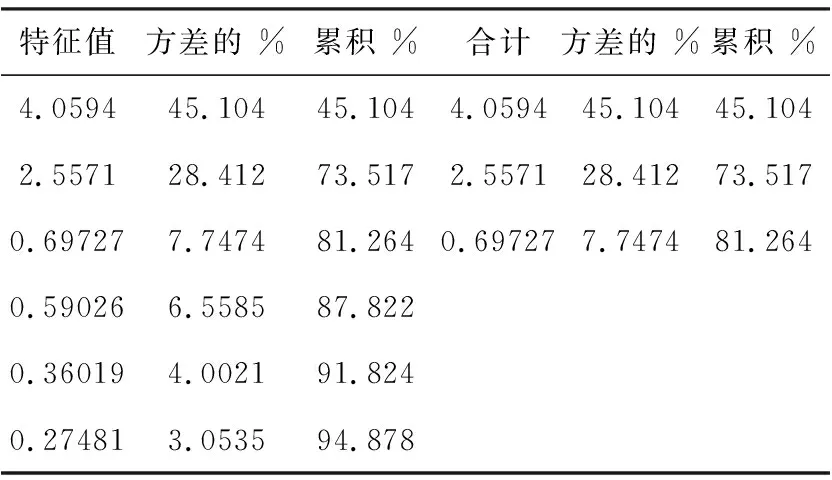
表2 相关特征值以及方差贡献率
表2是根据累积贡献达到80%以上选取的主成分,即提供了原始数据指标81.3%的信息,同时可以使原始指标的数量由9个下降到3个。相应的主成分因子载荷矩阵见表3。

表3 主成分因子载荷矩阵及特征向量矩阵
从表3可以看出,第一主成分对理数、生物、化学、物理几个分数解释的比较充分,第二主成分对语文、英语、政治、历史、地理几个分数解释的比较充分,已经包含了所有的科目。因此,第一、第二主成分的表达式为:
Z1=0.042x1+0.091x2+0.330x3+0.440x4+
0.450x5+0.449x6-0.343x7-0.260x8-0.314x9
Z2=0.410x1+0.443x2+0.324x3+0.169x4+
0.147x5+0.118x6+0.364x7+0.424x8+0.392x9由此可以得到学生各科排名的主成分综合成绩。接下来将排名主成分综合成绩与原始成绩、基于分数的主成分综合成绩进行统计比较,具体结果见表4。
表4原始成绩与排名主成分、分数主成分成绩的相关性

相关性原始成绩分数主成分排名主成分原始成绩10.9160.899分数主成分0.91610.994排名主成分0.8990.9941
从结果来看,三者具有很强的正相关性。
此外,利用线性函数进行回归分析见表5及图1.

表5 主成分成绩与原始成绩排名的线性回归分析
从结果来看,回归曲线的R2值为0.808,F值接近6000,二者的线性回归关系显著。
2.2 基于主成分分析法的指标权重
目前,主成分分析法在综合评价问题中的应用,主要体现在文中2.1所研究的综合成绩的分析上面,即相当于“样本评价”。其实,对于各个评价指标,也是可以进行综合评价的,甚至可以给出各个指标的“排名”,并由此确定各个指标的权重。
对导入的原始成绩数据做一个转置,利用同样的算法得到结果见表6:
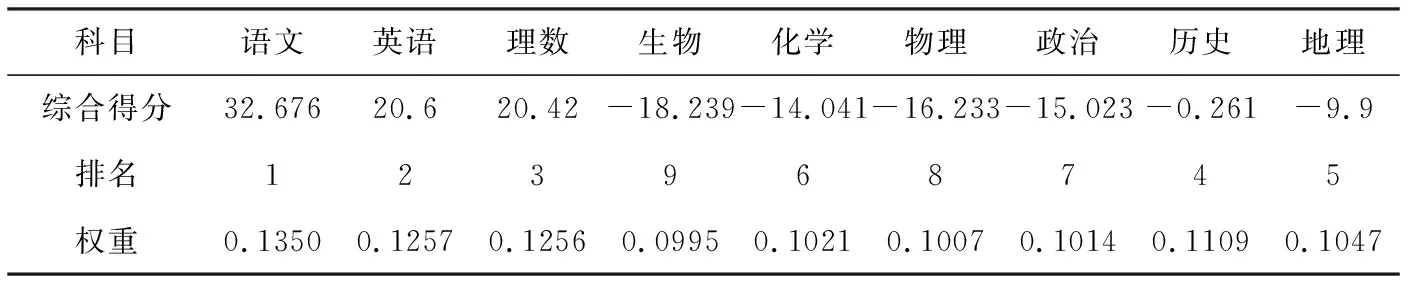
表6 各科主成分得分及权重

进一步考察该结果与原始排名的统计关系,结果见表7:
表7主成分权重综合成绩与原始成绩排名的线性回归分析

方程模型汇总R2Fdf1df2Sig.参数估计值常数b1线性.996317429.64811381.0001.500.998
从结果看,主成分权重下的综合成绩与原始成绩的相关性非常强,R2值达到了0.996。
2.3 综合评价结果分析
2.3.1 基于排名的主成分结果分析
从前面的结果来看,主成分权重的综合成绩以及排名的主成分综合成绩,与原始成绩排名的正相关性是比较显著的,但三者之间还是有明显差异的,那么这种差异反映了学生的学习状况,可参照前5个学生样本数据见表8。
表8提取前十个学生样本数据
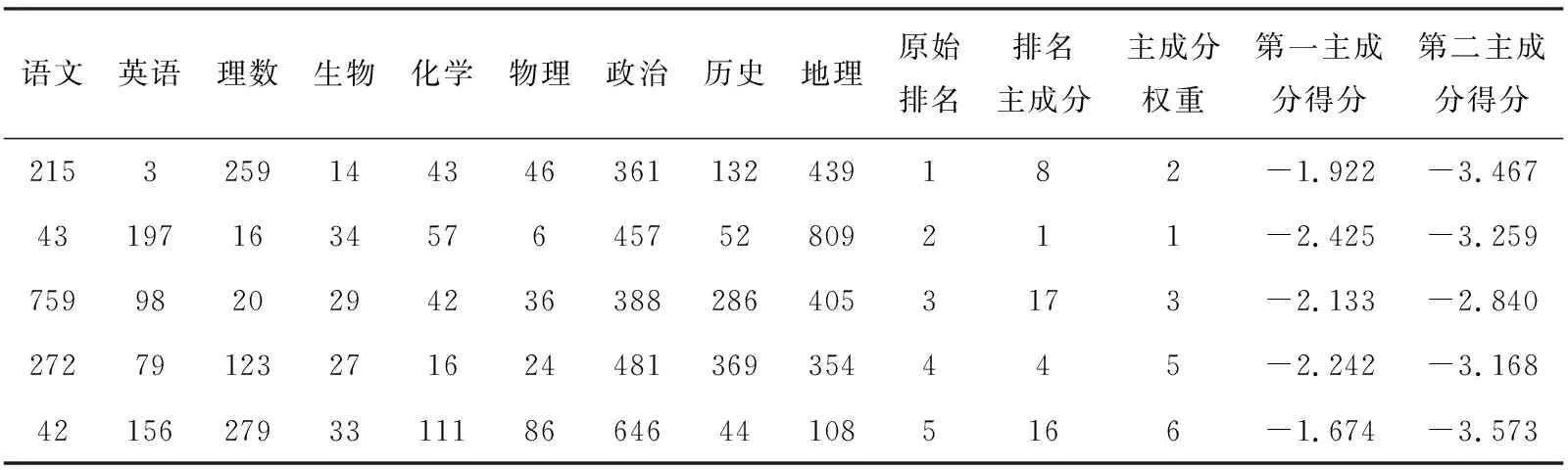
语文英语理数生物化学物理政治历史地理原始排名排名主成分主成分权重第一主成分得分第二主成分得分2153259144346361132439182-1.922-3.46743197163457645752809211-2.425-3.25975998202942363882864053173-2.133-2.84027279123271624481369354445-2.242-3.168421562793311186646441085166-1.674-3.573
从前5个学生的成绩来看,第一主成分分数的高低很好的反映了学生理科成绩的优劣。例如原始排名第二的学生第一主成分的得分最低,从成绩表上也明显能够看出该生的理科成绩很突出。此外,总分排名第一的学生,排名主成分综合成绩为第八,与原始成绩第二但排名主成分综合成绩第一的同学相比,能够看出,两个学生文理科排名各有高低,但第一名同学的理科成绩排名相对较低,从而导致综合排名下降。
2.3.2 主成分权重下的综合成绩分析
对于很多学生来说,未必在所有的科目上都能取得较好的成绩,即存在所谓的“偏科”现象,在“偏科”学生的心里,显然其所偏的科目在其心目中的重要性要更大一些。
主成分分析法作为基于数据的客观评价方法,得到的各个科目的权重,反映了该总体(某年级)实际的“偏科”程度,这对于全面衡量学生的综合能力是很有意义的。从具体计算结果看,2.2中得到的主成分权重综合评价结果与原始成绩的相关性很高,同时结果的差异也是比较明显的,原始总成绩高的在主成分权重综合成绩中的排名未必高。结合表1和表8中的数据,可以看到原始成绩排名第一的在主成分权重综合排名中排第二,说明该生在权重相对较大的科目中取得了相对较高的分数。
3 结 语
学生综合素质的评价,是一个多因素的复杂问题,分数作为其中一项重要的衡量方式,还是有较强的局限性的。因此,如何充分利用多种有效的成绩评价方法,对学生的综合成绩进行合理的评价就显得十分必要了。采用的评价方法能从某个角度说明成绩评价的内在意义,并具有现实的意义,希望能够给教育工作者以参考性的意见。
此外,研究对象是某一年级的全部学生,最终的排名是一个“大排名”,而从实际情况看,所采集的样本是来自于多个班级的,而各个班级内的综合成绩的研究以及班与班综合成绩的对比,也是有待进一步研究的。例如,学生在班级内的排名位置与其在整个年级的排名位置所反映的学生状态、某个班级在整个年级的排名位置所反映的班级状态等问题都是很有研究意义的,还有待进一步研究。
