钢-混凝土组合楼板对钢框架结构抗震性能的影响

李永梅，王 浩，李玉占，王 成



钢-混凝土组合楼板对钢框架结构抗震性能的影响

李永梅1, 2，王 浩1，李玉占3，王 成4

(1. 北京工业大学工程抗震与结构诊治北京市重点实验室，北京 100124；2. 北京工业大学城市与工程安全减灾省部共建教育部重点实验室，北京 100124；3. 中国核电工程有限公司河北分公司，石家庄 500021； 4. 中交第四公路工程局有限公司，北京 100022)

为了研究钢-混凝土组合楼板对钢框架结构抗震性能的影响，建立考虑楼板空间作用的梁-分层壳混合有限元模型和空框架模型．通过对两模型分别进行静力推覆分析和动力增量分析，揭示组合楼板对钢框架结构地震作用下弹塑性工作性能的影响规律．结果表明，组合楼板对梁产生增强作用，在地震作用下使结构抗侧刚度和抗侧承载力增大、结构周期和位移反应减小，但是考虑楼板组合作用的框架延性、滞回性能和耗能能力会降低，甚至可能改变结构预期的“强柱弱梁”的破坏模式，使结构偏于不安全．

钢框架；组合楼板；梁-分层壳混合模型；空间组合作用

房屋钢结构的楼板必须具有足够的承载力、刚度和整体性．压型钢板组合楼板具有性能优越、施工简便等特点，在钢框架结构住宅体系中应用广泛．钢框架结构体系采用组合楼板时，钢梁上翼缘通过抗剪连接件与压型钢板-混凝土组合楼板形成组合梁．竖向荷载作用下钢梁承受拉力、混凝土翼缘板承受压力，充分发挥两种材料的优势；侧向力作用下楼板和钢框架之间协同工作．《高层民用建筑钢结构技术规程》(JGJ,99—98)[1]建议：组合框架弹性分析时，中、边梁惯性矩分别取1.5倍、1.2倍钢梁惯性矩，以考虑楼板对组合梁刚度的贡献；但弹塑性分析时，不考虑楼板与钢梁的共同工作．试验表明[2]：即使进入弹塑性阶段，钢梁和混凝土楼板之间也存在显著的组合作用．由于规程建议的组合梁刚度放大系数值和钢梁相对于混凝土板的刚度无关，故对于钢梁相对楼板刚度较小的情况，可能会低估楼板空间组合作用对刚度的贡献、使设计偏于保守，而对于钢梁相对楼板刚度较大的情况，可能又会高估其贡献、使设计偏于不安全．

Northridge地震震后调查中发现，混凝土楼板与钢梁间的协同受力作用，造成大量梁柱节点的下翼缘应力水平偏高，提前发生脆性破坏[3]．因此，为了反映钢框架弹塑性受力全过程中楼板空间组合作用的工作机理和规律，本文建立合理考虑楼板组合作用的梁-分层壳混合有限元模型，研究楼板对结构抗震性能的影响，对于钢框架抗震设计具有现实意义．

１ 组合楼板的梁-分层壳混合有限元模型

针对壳-实体精细有限元模型计算效率较低而发展起来的梁-分层壳混合有限元模型(如图1(a)所示)，采用分层壳单元模拟组合楼板[4]，用梁单元模拟钢梁，用梁、壳节点耦合并设置偏心的方法实现楼盖的空间组合作用[5]．基于复合材料力学原理，将壳单元分成压型钢板层、混凝土板层和钢筋层，如图1(b)所示．压型钢板作为各向异性材料，计算分析时如果划分为细小的各向同性平板单元，必然会造成划分的单元数太多，实际工程设计难以实现，故将其按照等效为正交各向异性平板的方法，定义压型钢板层．在压型钢板层和钢筋层之间，划分成数层混凝土板层．按面积相等的原则，将焊接于压型钢板上的钢筋等效为钢筋层．通过制定材料角描述钢筋分布方向、将实配钢筋均匀“弥散”到该层的原理，计算得到压型钢板层、钢筋层的厚度．有限元计算时，首先得到壳单元中心层的应变和曲率，然后根据壳单元各层材料在厚度方向满足平截面假定，由中心层应变和曲率得到各钢筋和混凝土层的应变，由材料本构方程得到相应的应力，最后积分得到整个壳单元的内力．分层壳单元考虑了面内弯曲-面内剪切-面外弯曲之间的耦合作用，比较全面地考虑组合楼板在面内和面外的刚度和变形，更准确地反映结构的空间整体性能和各构件之间的协调关系．

需指出的是，梁-分层壳混合有限元模型可较为精细地考虑楼板对组合框架刚度和内力的贡献，但未考虑钢梁与混凝土板间的滑移效应．

图1 梁-分层壳混合有限元模型

2 工程模型

某3层住宅钢框架结构，首层、2层、3层计算高度分别为4.2,m、3.6,m、3.6,m，结构平面见图2．抗震设防烈度8度(0.2)，场地土类别Ⅱ类，设计地震分组为第2组．屋面为上人屋面．沿轴线布置混凝土空心小型砌块墙体．楼、屋面恒载(含板自重)标准值分别为6,kN/m2和6.5,kN/m2．底层柱脚、梁柱节点均为刚接．采用压型钢板-混凝土组合型楼板，压型钢板型号为YX-75-230-900(I)-1.2，板厚150,mm，栓钉按完全剪力连接设计．应用PKPM2010版软件STS、SATWE模块，将中梁、边梁刚度分别放大1.5倍、1.2倍[1]，按结构抗震等级为2级的“梁铰型”破坏机制进行抗震设计．混凝土强度为C30，楼板钢筋采用上下两层分离式配筋，上、下层配筋率分别为0.6%,和0.3%．梁柱选用钢材Q235B，楼板钢筋采用HRB400.梁、柱分别采用焊接H型钢和焊接方钢管，截面尺寸见表1．

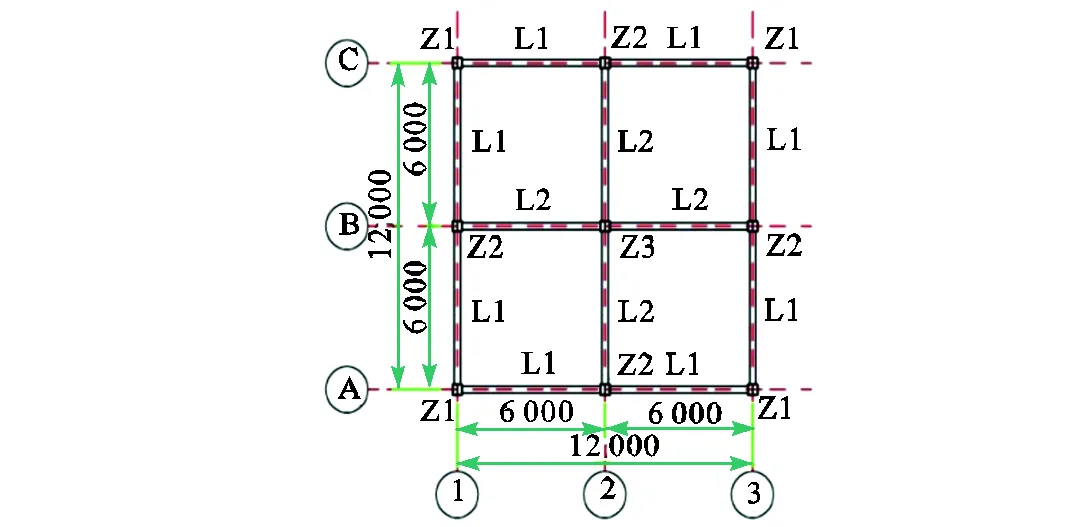
图2 结构平面布置

表1 框架截面

Tab.l Crosssection of the frame

构件编号截面尺寸/mm 柱Z1方钢管 B300×10 Z2方钢管 B300×14 Z3方钢管 B300×16 梁L1H200×200×7×9 L2H300×250×7×9

对节点域、梁、柱截面尺寸采用多重控制原则，即结构构件设计应力比达到0.9左右，且分别满足多遇、罕遇地震作用下弹性、弹塑性层间位移角变形控制条件；符合2级框架抗震等级“强柱弱梁、强剪弱弯”、节点域等各项抗震措施要求．

根据PKPM计算结果，采用SAP2000有限元分析软件，在保持结构质量分布基本不变的情况下，建立是否考虑楼板组合效应的两种框架对比模型，如图3(a)、(b)所示．

图3 有限元模型

模型A为梁-壳混合有限元模型，即楼板采用分层壳，梁、柱采用框架单元，通过壳元与梁元共用节点来模拟梁板协同工作．模型B为无楼板的空框架模型，即仅采用框架单元．模型A重力荷载代表值按1.0倍恒载＋0.5倍活载的面荷载施加在分层壳表面.

模型B按照梁端弯矩相等的原则，将楼板面荷载折算成梁上线荷载进行计算，以保证两个模型的总质量基本相同．

钢筋、混凝土本构关系分别如4(a)、(b)所示．通过离散铰来考虑梁柱的非线性行为[5]．梁单元采用主方向的3铰，柱单元采用-2-3铰．对于-2-3铰，指定一个屈服面来代表对轴力、次弯矩2和主弯矩3的不同组合最先屈服的位置．-2-3曲线和单轴3曲线形状相同，且均关于原点对称，如图4(c)所示．钢材、混凝土分别为Kinematic强化模型和Takeda模型[6-7]，滞回曲线如图4(d)、(e)所示.

图4 钢筋、混凝土和塑性铰本构关系及滞回曲线

3 结构静、动力弹塑性分析

首先，由模态分析得到结构自振周期．考虑楼板空间组合作用的模型A和空框架模型B前两阶平动振型周期分别为0.74,s、0.86,s，第3阶扭转周期为0.56,s；PKPM计算模型前两阶平动周期为0.72,s、0.75,s，第3阶扭转周期为0.53,s．由此可见，模型A与PKPM模型自振周期非常接近，说明有限元分析模型的合理性．另外，由于楼板的约束效应，使结构的整体刚度增加，故模型A比模型B自振周期减小，结构地震作用增大．

3.1 结构静力推覆分析

通常情况下，采用均匀分布形式将得到Pushover曲线的下限[5]，故选择均匀分布形式对两模型分别进行考虑-效应的Pushover推覆分析，得到两模型基底剪力-顶点位移曲线，如图5所示．

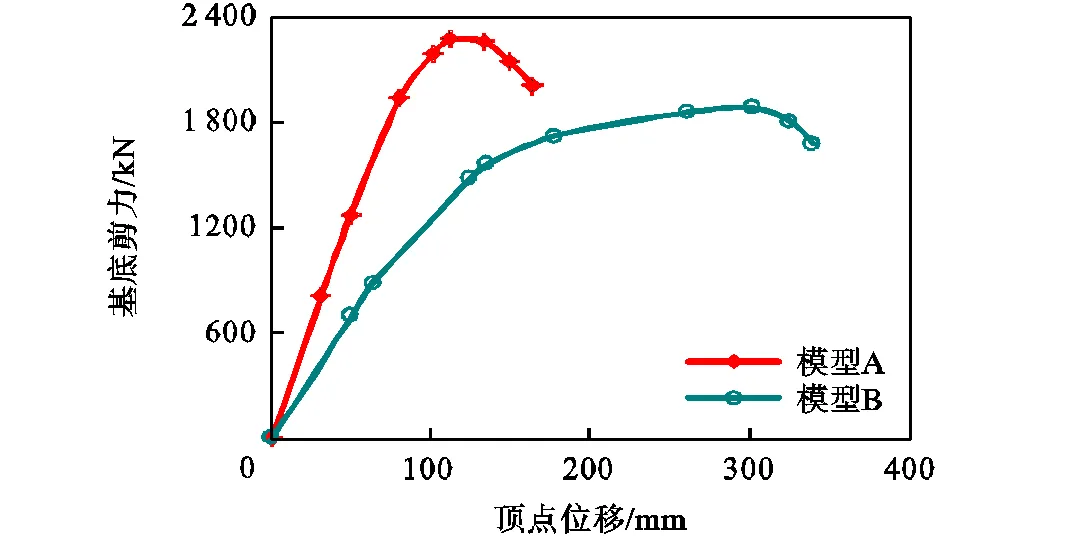
图5 基底剪力-顶点位移曲线

由图5可见，两模型均经历从弹性到弹塑性，再到屈服，最终进入失稳状态．模型A、B最大基底剪力分别为2,266,kN和1,879,kN，最大顶点位移分别为112,mm和302,mm．模型A基底剪力比模型B提高了20.6%,；但顶点位移减小了62.9%,．两模型相比，由于模型A组合楼板和梁组合在一起协同工作，对结构的承载力以及刚度影响很大，其顶点位移明显小于模型B，但是模型A最大基底剪力显著大于模型B．结构整体进入屈服阶段后，模型A较模型B水平段短．由此说明，模型A较模型B的抗侧刚度及侧向承载力显著提高，但延性显著降低．即忽略楼板空间组合作用的空框架模型低估了结构实际承受的地震剪力，高估了结构延性．这与文献[5]结论一致.

3.2 结构动力增量分析

选用具有代表性的EL-Centro(1,940,NS)波和Kobe(1,995,NS)波，采用Rayleigh阻尼体系，在不同地震峰值加速度强度(简称PGA)下，分别对两模型进行一簇结构动力弹塑性分析[8]，获得每级PGA下结构的最大层间位移角和最大顶点位移角，绘制最大层间位移角和最大顶点位移角与PGA的关系曲线，如图6和图7所示．

由图6、图7可见，两模型最大层间位移角和最大顶点位移角起始段均存在一个明显的直线段范围；随着PGA增加，呈现出曲线，直至曲线趋于水平直线、斜率趋于零．这表明结构经历从弹性到弹塑性，再到屈服，最终进入整体动力不稳定状态．对比两模型曲线可知：在相同地震动作用下，模型A最大层间位移角和最大顶点位移角均小于模型B．这说明组合楼板和钢梁组合在一起，能够对梁产生增强作用，使结构抗侧刚度增大、位移反应减小．另外，模型A、模型B在EL-Centro波和Kobe波作用下，当PGA分别达到700 gal、800 gal和790 gal、860 gal时，发生动力失稳破坏．由此可见，两种地震动作用下，考虑组合楼板作用的模型A较空框架模型B的极限承载力分别降低14.3%和8.9%．这与Pushover分析“模型A较模型B侧向承载力提高”的结果相悖．

（a）EL-Centro波

（b）Kobe波

图6 最大层间位移角与PGA的关系曲线

Fig.6 Relationship curves between the maximum story-drift ratio and PGA

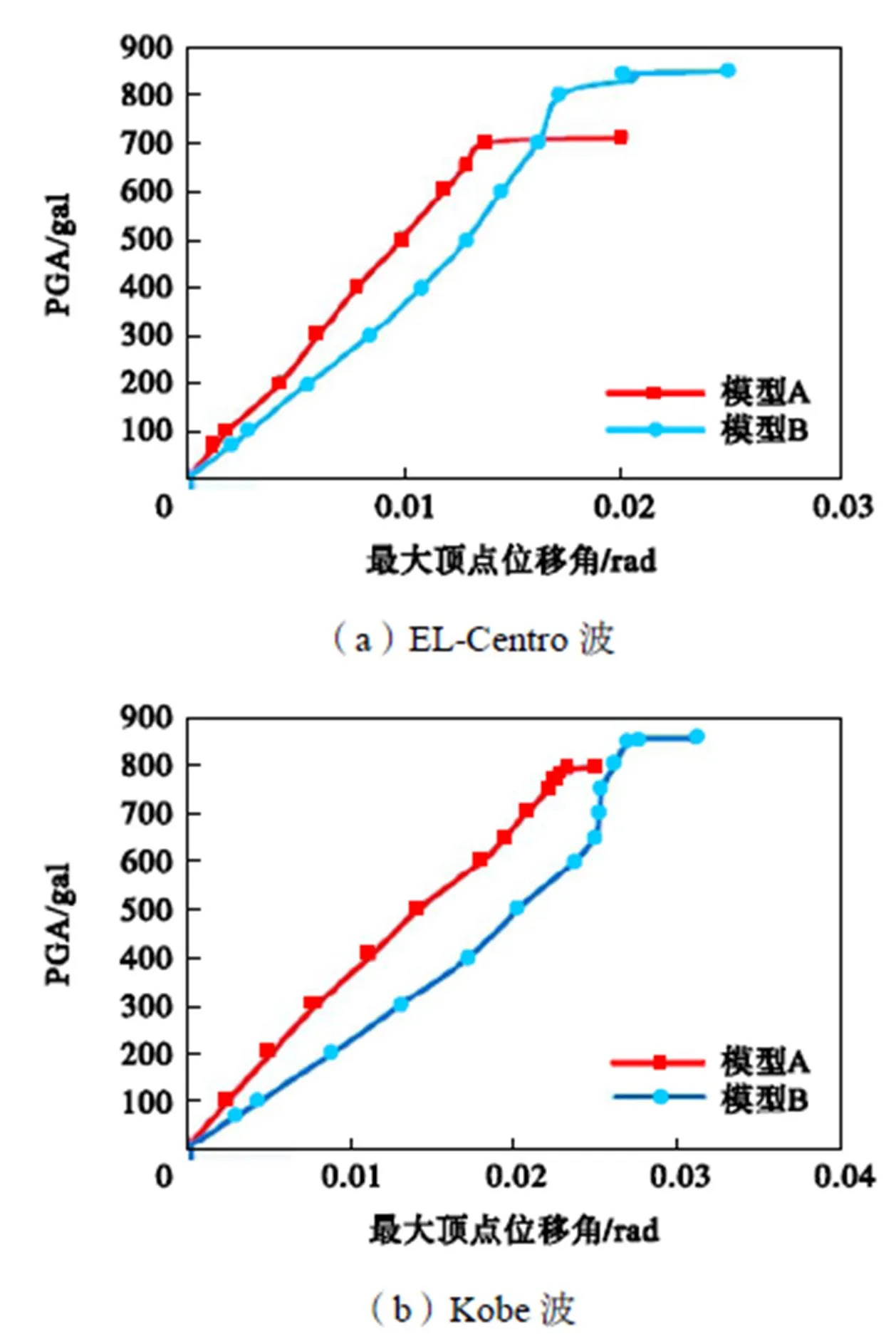
图7 最大顶点位移角与PGA的关系曲线

4 地震作用下组合楼板影响结构破坏模式的机理

仍采用上述算例，分析组合楼板框架模型和空框架模型在地震作用下的层间位移角分布、临界失稳时塑性铰分布、滞回曲线和组合楼板参与受力的程度．

4.1 顶点位移与基底剪力关系

在EL-Centro波和Kobe波作用下，当PGA达到模型A动力失稳破坏的700,gal时，两模型基底剪力与顶点位移曲线如图8所示．

图8 基底剪力与顶点位移关系曲线(PGA＝700,gal)

由图8可见，在两条地震波作用下，由于混凝土板裂缝开闭及滑移的影响，两模型顶点与基底剪力的滞回环形状明显不同；带楼板模型A滞回环形状呈非对称，空框架模型B滞回曲线正反方向基本呈现对称，且滞回环圆滑、饱满．由此表明，空框架结构的耗能能力显著优于有组合楼板的框架结构．

由图8还可见，EL-Centro波、Kobe波作用下，当PGA达到700,gal时，模型A最大基底剪力分别为2,044,kN和2,069,kN，最大顶点位移均为129,mm；模型B最大基底剪力分别为1,655,kN和1,649,kN，最大顶点位移分别为184,mm和209,mm.与模型B相比，模型A基底剪力分别提高了23.5%,和25.5%；但顶点位移分别减小了29.9%,和38.3%.由此可见，因组合楼板使结构的侧向刚度增大，在相同地震作用时，模型A最大基底剪力明显大于空框架模型B，但延性亦明显降低．综上所述，空框架结构的耗能能力和延性显著优于有组合楼板的框架结构.

另外，注意到当结构发生推覆破坏时，用Pushover方法求得模型A最大基底剪力2,266,kN、最大顶点位移112,mm，与结构发生动力失稳破坏相比，大约是IDA方法求得结构最大基底剪力的1.1倍、最大顶点位移的92.4%,．由此可见，两种方法求得的结构最大基底剪力和最大顶点位移基本一致．

4.2 层间位移角分布

在EL-Centro波多遇、设防、罕遇地震作用下，以及模型A达到动力临界失稳数值700,gal时，两模型各层最大层间位移角分布如图9所示．

由图9(a)～(c)可知，在多遇、设防和罕遇地震作用下，两模型最大层间位移角均发生在第2层，模型A各层最大层间位移角均小于模型B；但由图9(d)可知，当PGA达到动力临界失稳700,gal时，模型A、B最大层间位移角分别发生在首层和第2层，且首层模型A最大层间位移角大于模型B．由此说明，组合框架底层的位移反应比空框架大，组合楼板改变了结构的破坏模式．

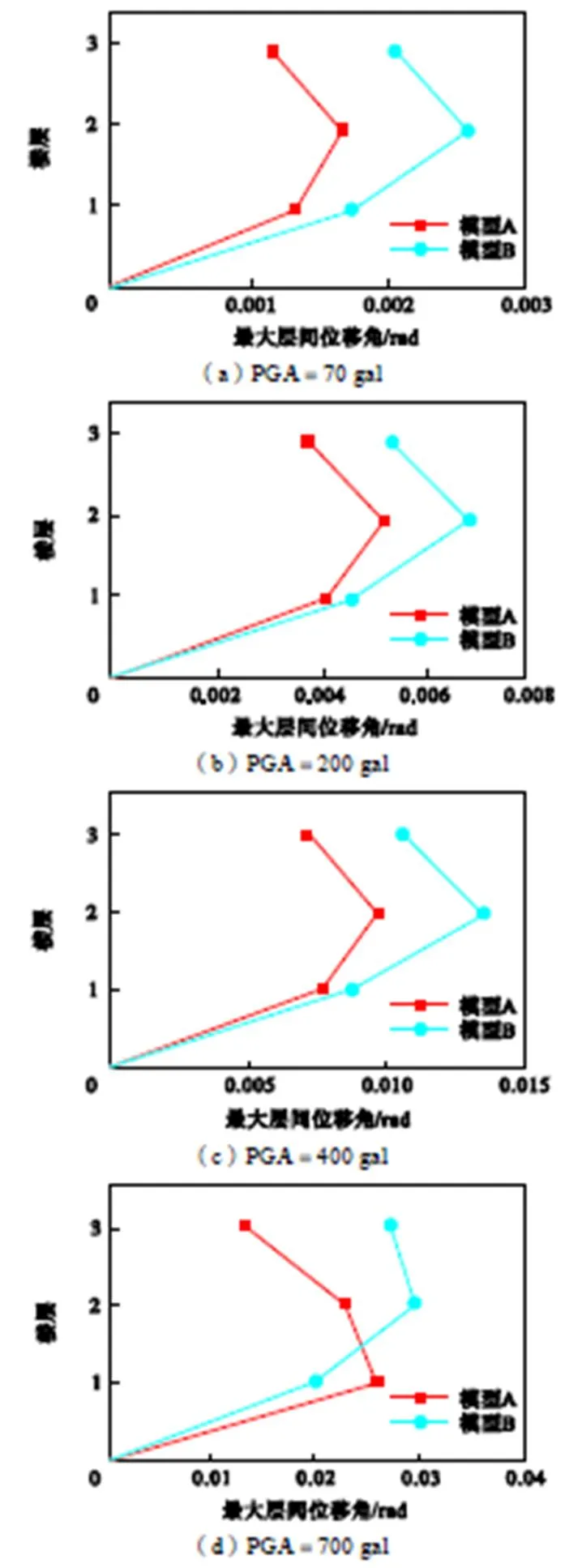
图9 各级地震水平作用下最大层间位移角分布

4.3 塑性铰分布情况

考察EL-Centro波作用下两模型临界失稳时，塑性铰分布情况，如图10所示．

由图10可见，当结构临界失稳时，两模型首层柱底端均出现了塑性铰，模型A柱铰数量多于模型B、梁端塑性铰少于模型B．模型A首层柱底和柱顶均出现塑性铰，形成柱上、下端同时出铰的“层侧移机构”，此时梁端塑性铰发展处于初期阶段，属于典型“强梁弱柱”脆性破坏模式．模型B仅首层柱底端出现塑性铰，且梁端塑性铰发展比较充分，属于“强柱弱梁”延性破坏模式．究其原因，主要是组合楼板和钢梁共同作用，提高了梁的抗弯刚度以及抗弯承载力，模型A底层柱先于梁进入屈服，底层的位移反应比空框架模型B大，直接导致预期的“强柱弱梁”破坏机制难于实现．

图10 临界失稳时塑性铰分布情况

4.4 组合楼板参与结构受力的程度

图11 模型A梁端、柱端最大弯矩与PGA的关系曲线

表2 模型A梁端、柱端最大弯矩之和与PGA的关系

Tab.2 Relationship between the maximum moment at the end of beam or column and PGA for model A

5 结 论

(1) 梁-分层壳混合有限元模型可较为精细地考虑楼板对组合框架刚度和内力的贡献．

(2) 楼板的空间组合作用在框架体系弹性及弹塑性受力的全过程中始终存在．

(3) 尽管静、动力弹塑性分析求得的空框架结构和带楼板框架结构模型的最大基底剪力和最大顶点位移基本一致，但是两种分析模型是否考虑楼板的组合作用，求得的极限承载力规律截然不同，即Pushover分析求得“带楼板模型较空框架模型侧向承载力提高”、而IDA分析得到“带楼板模型求得的结构动力极限承载力小于空框架模型”的结论．

(4) 由于楼板的组合作用，使结构的整体刚度增加，自振周期减小，结构地震作用增大，位移反应减小，延性、滞回性能和耗能能力降低．

(5) 楼板加强了钢梁的抗弯刚度和抗弯承载力；对梁、柱弯矩分配、塑性铰出现位置影响较大．在强烈地震作用下由于考虑楼板组合作用导致大幅度提高的梁端抗弯承载力被低估、“超强”现象严重，最终改变结构预期的“强柱弱梁”破坏模式、发生结构倒塌现象．

(6) 钢-混凝土组合框架结构设计宜考虑钢梁和楼板的组合作用，避免框架梁“超强”导致梁端承载力被低估、“强柱弱梁”的抗震设计准则达不到预期、结构偏于不安全的情况出现．

［1］ JGJ 99—98 高层民用建筑钢结构技术规程[S]. 北京：中国建筑工业出版社，1998.

JGJ 99—98 Technical Specification for Steel Structure of Tall Building[S]. Beijing：China Architecture & Building Press，1998(in Chinese).

［2］ 石永久，苏 迪，王元清. 混凝土楼板对钢框架梁柱节点抗震性能影响的试验研究[J]. 土木工程学报，2006，39(9)：26-32.

Shi Yongjiu，Su Di，Wang Yuanqing. An experimental study on the seismic performance of beam-column joints in steel frames with the effect of concrete slabs considered[J].，2006，39(9)：26-32(in Chinese).

［3］ 聂建国，陶慕轩，黄 远，等. 钢-混凝土组合结构体系研究新进展[J]. 建筑结构学报，2010，31(6)：71-80.

Nie Jianguo，Tao Muxuan，Huang Yuan，et al. Research advances of steel-concrete composite structural systems[J].，2010，31(6)：71-80(in Chinese).

［4］ 北京金土木软件技术有限公司. SAP2000中文版使用指南[M]. 北京：人民交通出版社，2012.

Beijing Gold Civil Software Technology Co LTD.2000[M]. Beijing：China Communication Press，2012(in Chinese).

［5］ 陶慕轩，聂建国. 考虑楼板空间组合作用的组合框架体系设计方法(Ⅱ)-刚度及验证[J]. 土木工程学报，2013，46(2)：39-50.

Tao Muxuau，Nie Jianguo. Design guidelines of composite frame systems considering the slab spatial composite effect-Part Ⅱ：Stiffness and verifications[J].，2013，46(2)：39-50(in Chinese).

［6］ Hejazi F，Zabihi A，Jaafar M S. Development of elasto-plastic viscous damper finite element model for reinforced concrete frames[J].，2014，42(5)：284-293.

［7］ Hwang H M，Jaw J W. Probabilistic damage analysis of structure[J].，，1990，116(7)：1992-2007.

［8］ 徐龙河，单 旭，杨冬玲，等.考虑损伤累积效应的钢框架结构抗震分析与设计[J]. 天津大学学报，2012，45(6)：493-498.

Xu Longhe，Shan Xu，Yang Dongling，et al. Seismic analysis and design for steel frame structure considering damage accumulation effects[J].，2012，45(6)：493-498(in Chinese).

(责任编辑：樊素英)

Influence of Steel-Concrete Composite Slab on Seismic Behavior of Steel Frame Structure

Li Yongmei1, 2，Wang Hao1，Li Yuzhan3，Wang Cheng4

(1．Beijing Key Laboratory of Earthquake Engineering and Structural Retrofit，Beijing University of Technology， Beijing 100124，China；2．Key Laboratory of Urban Security and Disaster Engineering，Ministry of Education， Beijing University of Technology，Beijing 100124，China； 3．Hebei Branch Company of China Nuclear Power Engineering Co.，Ltd，Shijiazhuang 500021，China 4．CCCC Fourth Highway Engineering Co.，Ltd，Beijing 100022，China)

In order to study the influence of steel-concrete composite slab on the seismic behavior of steel frame structure，the beam-stratified shell mixed models of profiled steel sheeting-concrete composite slabs are set up with the spatial composite effect on slabs taken into consideration．Pushover analysis and dynamic incremental analysis are made，respectively，of a steel frame structure with and without slabs，and the influence of composite slabs on the seismic behavior of steel frame structure in elasto-plastic working state under earthquake is presented．It can be found that the slab spatial composite effect will enhance the strength of beams so as to increase structural lateral stiffness and bearing capacity and decrease structural period and displacement response．But the slab spatial composite effect may reduce structural ductility，hysteresis quality and energy dissipation，and even change the structural expected failure mode of“strong column and weak beam”，which is likely to make the structure unsafe.

steel frame；composite slab；beam-stratified shell mixed model；spatial composite effect

the Natural Science Foundation of Beijing，China(No.,8152008).

TU398；TU318

A

0493-2137(2018)11-1181-07

2018-01-07；

2018-04-16.

李永梅（1971—  ），女，副教授.

李永梅，liym@bjut.edu.cn.

北京市自然科学基金资助项目(8152008).

10.11784/tdxbz201801047