螺旋线插补速度规划及其插补参数求解方法

王太勇，尤中桐，辛全琦



螺旋线插补速度规划及其插补参数求解方法

王太勇，尤中桐，辛全琦

(天津大学机械工程学院，天津 300350)

提出了一种基于曲率特性与7段式S型加减速的阿基米德螺线插补算法．该插补算法的速度规划综合考虑了螺旋线变半径特性与曲率特性对运行速度的持续限制，以求得到合理的速度规划结果．针对一般插补参数求解方法存在较高速度波动率的问题，设计了一种基于改进牛顿迭代的预估-校正法．该方法以1阶泰勒展开法求解迭代初值，然后利用改进牛顿迭代计算限定的次数得到精确值，最后通过仿真对比与实验说明其优势与应用价值，该方法可有效降低速度波动率，且满足数控系统实时性要求．

阿基米德螺线；加减速规划；速度波动；改进牛顿迭代

制造业迅猛发展，在航空、航天、汽车、模具制造等领域，复杂曲线类零件的应用越来越广泛．是否具有空间参数曲线实时插补功能，是衡量数控系统加工能力的一个重要标志[1]，然而除少数国外高端数控系统(西门子840D、法那科30i等)具有复杂参数曲线插补功能外，国内大多数数控系统通常只提供直线、圆弧插补功能[2-3]，所以拓展插补功能是数控技术领域创新性发展的重要任务之一．在这方面，一些学者立足于阿基米德螺线(简称为螺旋线)的工程实际应用，进行了其数控加工方法研究，大致可划分为以下3个方向．

(1) 基于时间分割法．罗良玲等[4]基于时间分割思想，以当前点位置与一个插补周期内的进给量作为已知条件，推导出插补点间的递推公式，进而求得各轴的增量．但是递推公式成立的前提是参数增量足够小，而这会限制最大运行速度，降低效率．

(2) 基于数控系统宏功能．针对内置锥形螺纹与螺旋线形凸轮的加工，刘萍等[5]、邵伟平[6]与沈文华等[7]分别设计了基于FANUC宏程序的螺旋线插补模板．但是其本质是基于等参数法的小线段或小圆弧段逼近螺旋线，然后再进行直线、圆弧插补，该逼近计算过程由数控系统完成，增加了计算负担，影响实时性．

(3) 基于极坐标机床．Qiu等[8]提出了一种采用微段螺旋线逼近待加工曲线的拟合算法，并详细分析了逼近误差，但是微段螺旋线的加工需要借助极坐标数控机床．鉴于此，Hu等[9]搭建了基于极坐标系的加工平台，利用数控转台转动与线性轴径向移动合成螺旋线轨迹．但是加工时，螺旋线中心必须与数控转台回转中心重合，这就给工件的装夹、调整带来了不便.

本文以螺旋线参数化插补为出发点，提出了一种基于曲率特性与7段式S型加减速[10]的螺旋线插补算法．阐述了该插补算法的速度规划方法，引入自适应插补的概念，考虑了曲率变化对运行速度的持续限制，保证在插补精度、柔性加减速等约束条件下得到合理的速度规划结果．利用加权与相似三角形原理，提出了一种基于改进牛顿迭代的预估-校正法来求解插补参数，阐明了其计算原理，最后通过仿真与实验说明其优势与应用价值：在满足数控系统实时性要求的前提下，能有效降低速度波动率，减少迭代次数．

1 阿基米德螺线方程

阿基米德螺线是一种平面二维曲线．在《论螺线》一书中，阿基米德给出了如下定义：当一点沿动射线以等速率运动的同时，这条射线又以等角速度绕点旋转，点的轨迹被称为“阿基米德螺线”．

如图1所示，假设射线的初始长度为0，其与轴的初始夹角为0，点的运动速率为0，那么阿基米德螺线的极坐标方程可表示为

 (1)

式中：为点到坐标系原点的距离；为射线与轴正向的夹角；0与0为常数．

由式(1)可得到对应的直角坐标参数方程为

 (2)

利用微积分方法，可以得到螺旋线的弧长积分公式为

(3)

进一步可求得式(3)对应的1阶导数为

(4)

更一步可求得式(3)对应的2阶导数为

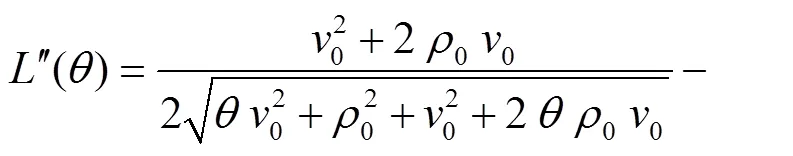
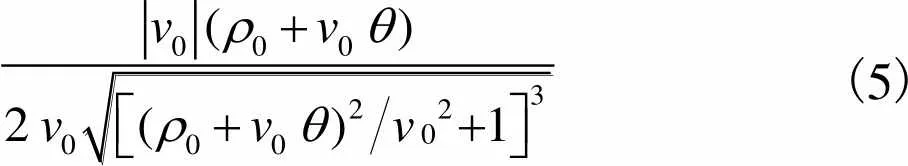
(5)

由2阶泰勒展开式得到

(6)

进一步变换，可得

(7)

所以已知弧长与当前位置参数1，求解式(7)这个一元二次方程可得到对应的位置参数增量．

2 基于弓高误差约束的螺旋线自适应插补

参数曲线插补计算过程中，主要包括径向误差和弓高误差，由于径向误差很小，通常可以忽略[11]．为保证加工精度，实时插补时相邻插补点间的弓高误差必须在允许范围内．图2为插补点间的弓高误差示意图，其中ER为弓高误差，r为当前插补点的曲率半径，L为当前插补点与下一插补点之间的直线距离，θ和θ1分别为当前插补点和下一插补点所对应的位置参数．由图2所示的几何关系，可得

 (8)

所以进给速度达到弓高误差约束后，在螺旋线曲率半径变化的持续限制下，进给速度

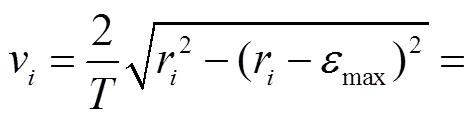
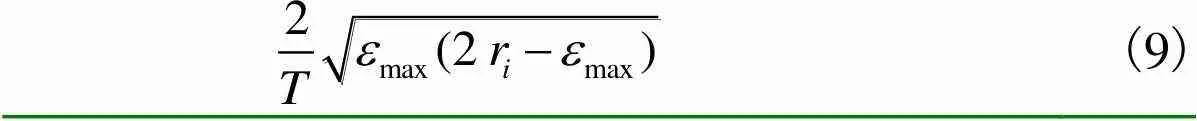
(9)

式中：为插补周期；v为该插补周期的进给速度；max为允许的最大弓高误差．

根据式(9)求出的实际进给速度，可以求得该插补周期内的位移，进而利用第4节的插补参数计算方法求得下一插补参数．

3 螺旋线插补算法的速度规划

3.1 速度规划原理

速度规划就是针对某一段参数已知的螺旋线，根据给定的起始速度、终止速度和编程速度，经过一系列计算判断，确定插补该段螺旋线的速度变化规律．由于本文在速度规划上综合了7段式S型加减速与基于弓高误差约束的自适应插补，所以速度规划结果最多由以下几部分组成：加速、匀速、减速、自适应速度变化．其中加、减速方式分为4种类型：①加加速-匀加速-减加速；②加加速-减加速；③加减速-匀减速-减减速；④加减速-减减速．

3.2 速度规划算法

假设起始速度为s，终止速度为e，编程速度为，最大加加速度为max，最大加速度为max，螺旋线起点处s与终点处e在弓高误差约束下的最大速度分别为s_ce与e_ce，由螺旋线的变半径特性可知，螺旋线上其他点在弓高误差约束下的最大速度均介于二者之间．另外这里只考虑s＜s_ce、e＜e_ce且s＜、e＜．根据编程速度与s_ce和e_ce的关系，分为3种情况进行讨论．

情况1≥s_ce且≥e_ce

超过了弓高误差约束下的最大速度，此时无需考虑对速度规划的影响，最大速度仅由弓高误差限制．接下来的关键就是根据起始速度，求解加速达到弓高误差约束速度的位置点与其对应的加速阶段时间．假设以s加速达到弓高误差约束速度的位置点参数为s_ce，根据式(10)可以计算，以起始速度进行加速度从0加到max而后减为0的加速过程所需要的距离S1，所需时间2,，速度变化量v1．螺旋线的总长为Stotal，可利用式(3)求得

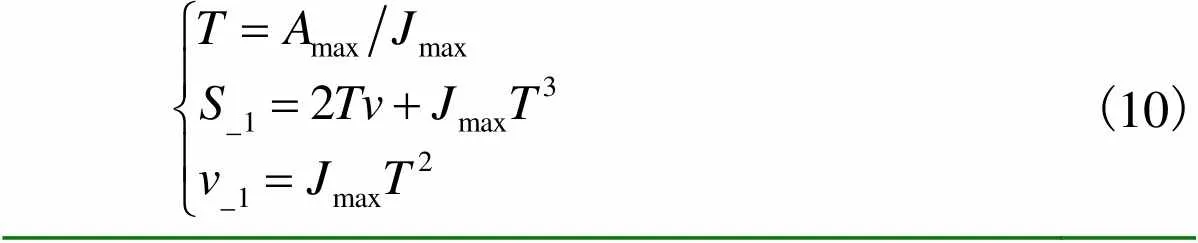
 (10)

(1) 若S1＞Stotal，则在求解s_ce时，加速方式一定为加加速-减加速，且s_ce一定位于区间[s，e]内．

(2) 若S1≤Stotal，则需要进一步判断当前速度_c＝s＋v1是否超过了当前位置点s_c处的弓高误差限制．由式(7)，代入＝S1与＝θ可求得Δ，进一步得到s_c＝s＋Δ，再利用式(1)与式(6)可得到当前位置点弓高误差限制的最大速度v．

若_c＜v，则在求解s_ce时，加速方式一定为加加速-匀加速-减加速，且s_ce一定位于区间[s_c，e]内．

若_c＞v，则在求解s_ce时，加速方式一定为加加速-减加速，且s_ce一定位于区间[s，s_c]内．

确定了加速方式与解所在的区间[ss，ee]，便可利用二分法求解s_ce的精确值．过程如下所述．

(1) 取区间中点temp＝0.5(ss＋ee)．

(2) 利用式(3)计算起始点s到中点temp的距离1，进而利用式(11)和式(12)计算运行到该点达到的速度1．

当加速方式为加加速-匀加速-减加速时，

 (11)

当加速方式为加加速-减加速时，

 (12)

(3) 根据该中点的位置参数temp，利用式(1)与式(6)得到弓高误差限制的最大速度2．

(4) 比较1与2的大小关系，缩小二分区间范围．若1与2之差满足精度要求，则停止计算，temp即为待求的s_ce．若1＜2，则令ss＝temp；若1＞2，则令ee＝temp；返回步骤(1)继续计算．

采用上述方法进行反向加速即可求得e_ce，这里不再赘述．

在求得了s_ce与e_ce后，根据二者的大小关系可确定整个螺旋线的速度规划结果：若s＜s_ce＝e_ce＜e，速度规划结果为加速[s，s_ce]-减速[s_ce，e]；若s＜s_ce＜e_ce＜e，速度规划结果为加速[s，s_ce]-自适应插补[s_ce，e_ce]-减速[e_ce，e]；若s＜e_ce＜s_ce＜e，则达不到弓高误差约束的最大速度，速度规划结果为加速[s，se]-减速[se，e]，这时需要求解实际的加速终点se．分析可知，此时加速终点对应的参数一定位于区间[e_ce，s_ce]内，采用二分法进行求解，步骤如下所述．

(1) 取区间中点temp＝0.5(e_ce＋s_ce)．

(2) 利用式(3)分别计算起始点s与e到中点temp的距离s与e，通过判断s(e)与_1的大小关系确定加速方式(对e来说是反向加速)，再利用式(11)或式(12)计算运行到该点达到的速度ss与ee，同时记录下相应的加减速方式．

(3) 比较ss与ee的大小关系，缩小二分区间范围．若ss与ee之差满足精度要求，则停止计算，temp即为待求的se．若ss＜ee，则令e_ce＝temp；若ss＞ee，则令s_ce＝temp；返回步骤(1)继续计算．

情况2介于s_ce与e_ce之间

相比于情况1，这里在求得了s_ce与e_ce后，还需要考虑编程速度与螺旋线半径变化趋势的影响．假设在弓高误差约束下对应的位置点参数为θ，若存在匀速段，其终点位置参数为ue(求法在后文给出)，螺旋线半径逐渐增大(即0＞0)．根据s_ce、e_ce与F三者的大小关系，可确定整个螺旋线的速度规划结果．若s＜F＜s_ce＜e_ce＜e，速度规划结果为加速[s，F-匀速[F，ue]-减速[ue，e]．若s＜s_ce＜F＜e_ce＜e，速度规划结果为加速[s，s_ce]-自适应插补[s_ce，F]-匀速[F，ue]-减速[ue，e]．若s＜s_ce＜e_ce＜F＜e，速度规划结果为加速[s，s_ce]-自适应插补[s_ce，e_ce]-减速[e_ce，e]．若s＜e_ce＜s_ce＜e，则达不到弓高误差约束的最大速度，按照前文二分法可求解实际的交汇点m与达到该点的速度m，然后比较与m的大小关系：若＜m，说明速度超限，速度规划结果为加速[s，F]-匀速[F，ue]-减速[ue，e]；若＞m，则无需考虑的影响，速度规划结果为加速[s，m]-减速[m，e]．若s＜e_ce＝s_ce＜e，则实际的交汇点即为s_ce(e_ce)，记达到该点的速度为m，比较与m的大小关系：若＜m，说明速度超限，速度规划结果为加速[s，F]-匀速[θ，ue]-减速[ue，e]；若＞m，则无需考虑的影响，速度规划结果为加速[s，s_ce]-减速[s_ce，θ]．

匀速段的终点位置参数ue可由下述方法求解．

(1) 通过判断－e与v1的大小关系，利用式(13)和式(14)求解e反向加速到所需要的时间，再进一步计算所运动的距离．

若－e＞v1，则有

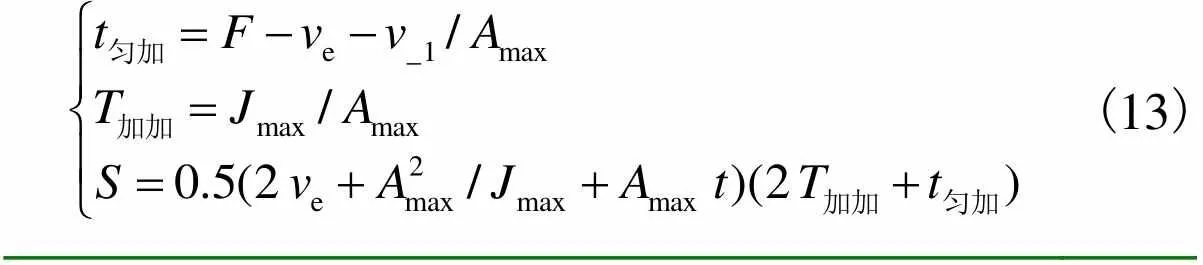
 (13)

若－e＜v1，则有

 (14)

(2) 利用式(7)求解参数增量Δ，进一步可得到ue＝e－Δ，同时记录其加减速方式．

采用相同的分析方法可得到螺旋线半径逐渐减小(即0＜0)情况下，整个螺旋线的速度规划结果．

情况3≤s_ce且≤e_ce

这时无需考虑弓高误差对运行速度的限制，问题转变为已知起始速度、终止速度、编程速度与运动距离的S型加减速规划，具体规划方法可参考文献[12]，这里不再赘述．

上述速度规划算法的完整流程如图3所示．

至此，根据速度规划结果与其对应的加减速方式，可求得各段的运行时间、关键点的速度、加速度、加加速度等信息，为求解插补参数做准备．

需要说明的是，上述算法中的二分法在实际应用过程中，二分次数仅十几次就可以达到计算要求，并不会对数控系统的实时性造成太大影响．

图3 速度规划算法流程

4 插补参数实时计算

插补点计算的关键在于插补参数的求解，即已知当前插补参数与该插补周期内的位移，求解下一插补参数，其求解的精度与速度直接决定了最终的插补效果与加工质量．常用的泰勒展开法在求解插补参数时，由于存在截断误差，导致插补点求解不够精准，引起较大的速度波动．鉴于此，本文采用了一种基于改进牛顿迭代的预估-校正法，其原理如下．

4.1 预估初值的确定

由1阶泰勒展开式可知

 (15)

式中：θ为已知的当前插补参数；θ＋1为待求的下一插补参数；Δ为两点间的弧长．将该插补周期内移动的距离代入式(15)可得到下一插补参数

 (16)

利用式(16)即可计算得到下一插补参数的预估初值，为后续的迭代校正所用．

4.2 改进牛顿迭代

假设(θ)与(θ＋1)分别为当前插补点与所求下一插补点的位置，根据速度波动率[13]的定义可构造函数

 (17)

实际求解θ＋1时，通常期望式(17)等于0，即不存在速度波动．由于式(17)为复杂的非线性方程，这里采用数值解法——改进牛顿迭代进行求解，迭代初值采用预估初值．

迭代公式如下：

 (18)

与传统的牛顿迭代不同的是，改进牛顿迭代在每次迭代计算后并不是把本次迭代计算得到的结果直接作为下次迭代的输入值，而是按照下述基于加权与相似三角形原理的规则进一步求解下次迭代的输入值，使其更接近理想解，以加快收敛速度．

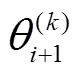
 (19)

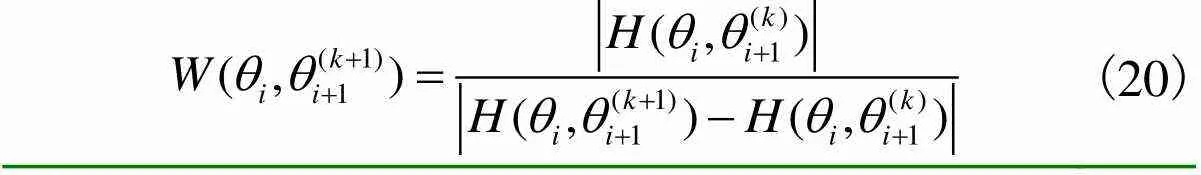
 (20)

 (21)

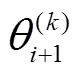
(22)

(23)

图5 理想解大于二者

图6 理想解小于二者

4.3 插补参数计算流程

根据第4.1节与第4.2节所述内容，可以得到插补参数的计算流程如图7所示，具体步骤如下所述．

图7 插补参数计算流程

5 算法仿真与分析

上文算法已经通过C语言编程实现，获得的数据利用Matlab R2014b进行可视化，在计算机上进行该算法的仿真测试分析．测试环境如下：操作系统为Windows 7旗舰版；内存为8,GB；CPU为Inter(R) Core(TM)i5-4570 3.20,GHz×4；显卡为AMD Radeon HD 8490．

这里仅以螺旋线＝10＋/π(∈[0，π])(此时0＞0，0＜0时与此类似，就不再占用篇幅分析)作为待插补曲线，通过给定不同的初始条件，获得对应的速度与加速度曲线，说明其正确性．假设最大加加速度max＝10,000,mm/s3，最大加速度max＝1,000mm/s2，插补周期＝0.002,s．对应不同的最大允许弓高误差max、初始速度s、终止速度e以及编程速度，可以规划得到不同的速度与加速度曲线.这里给出4种较为典型的情况，其他情况就不再一一罗列．

(1) 最大允许弓高误差max＝0.000,5,mm，初始速度s＝96,mm/s，终止速度e＝102,mm/s，编程速度＝200,mm/s．速度规划结果为加速-自适应插补-减速，对应的速度与加速度曲线如图8所示．

(2) 最大允许弓高误差max＝0.000,5,mm，初始速度s＝96,mm/s，终止速度e＝98,mm/s，编程速度＝103,mm/s．速度规划结果为加速-自适应插补-匀速-减速，对应的速度与加速度曲线如图9所示．

图8 情况1速度与加速度曲线

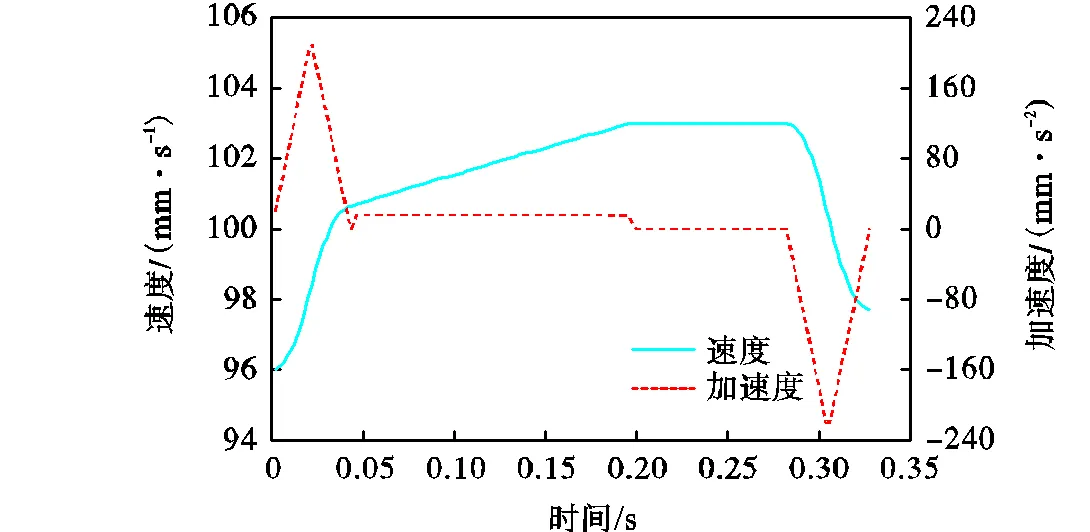
图9 情况2速度与加速度曲线

(3) 最大允许弓高误差max＝0.001,mm，初始速度s＝0,mm/s，终止速度e＝0,mm/s，编程速度＝141.5,mm/s．速度规划结果为加速-匀速-减速，对应的速度与加速度曲线如图10所示．可由加速度曲线看出，放大的部分是很短暂的匀速过程．

图10 情况3速度与加速度曲线

(4) 最大允许弓高误差max＝0.001,mm，初始速度s＝0,mm/s，终止速度e＝0,mm/s，编程速度＝140,mm/s．速度规划结果为加速-减速，对应的速度与加速度曲线如图11所示．

图11 情况4速度与加速度曲线

为了证明基于改进牛顿迭代的预估-校正法的优越性，以上述情况4作为初始条件，对传统的2阶泰勒展开法、2阶Runge-Kutta附加补偿值的方法[14]、基于一般牛顿迭代预估-校正法[15-16]和本文所提基于改进牛顿迭代的预估-校正法的计算精度进行了比较，同时对比了除去2阶泰勒展开法外，计算精度较高的其他3种方法的计算效率．其中两种预估-校正方法的要求速度波动率精度为10-10，最大迭代次数为5．

图12所示为4种方法计算插补参数时的速度波动率对比，其中2阶泰勒展开法的速度波动率远远大于其他3种方法，最大约为3.8%,，2阶Runge-Kutta附加补偿值的方法的速度波动率小于2阶泰勒展开法的速度波动率，但高于两种预估-校正法的速度波动率，最大约为0.19%,．

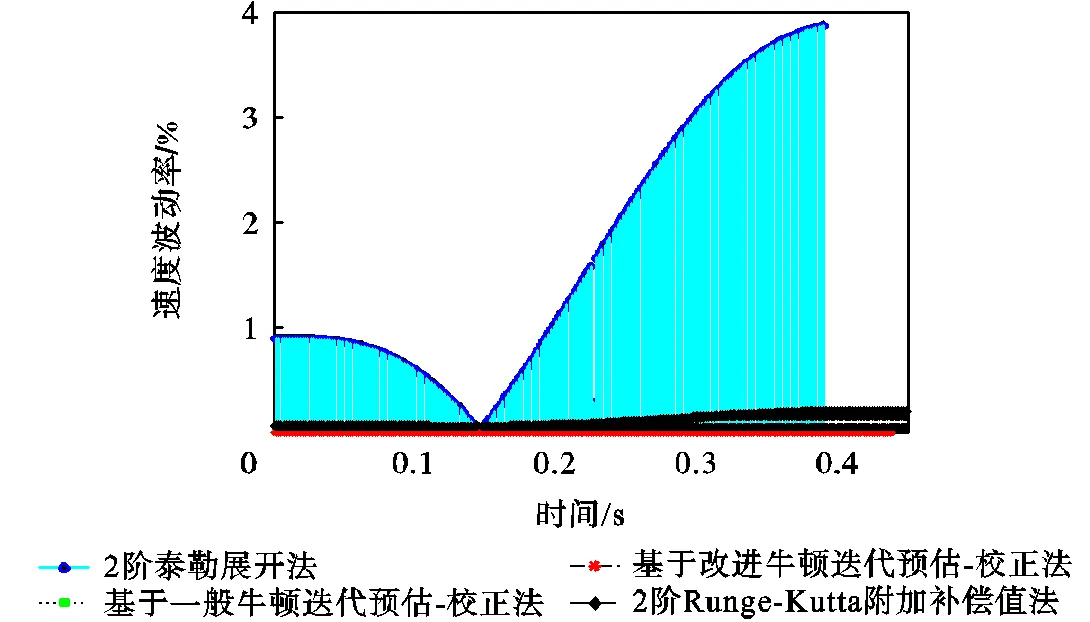
图12 4种方法的速度波动率对比

图13所示为精度最高的两种预估-校正法计算插补参数时的速度波动率对比，可见二者的计算精度大致相同，均达到10-11级．

图14所示为4种方法的计算耗时对比．从计算耗时的角度看，由于2阶泰勒展开法和2阶Runge-Kutta附加补偿值的方法不存在迭代计算，均耗时较少；两种预估-校正法的计算耗时尽管高于2阶泰勒展开法和2阶Runge-Kutta附加补偿值的方法，但远小于插补周期2,ms，整体上基于改进牛顿迭代的预估-校正法平均耗时少于基于一般牛顿迭代的预估-校正法．图15所示为两种预估-校正法的迭代次数对比．从迭代次数的角度看，二者迭代次数均在5次以内，但是基于改进牛顿迭代的预估-校正法在部分区域的迭代次数更少，可见其计算效率更高．

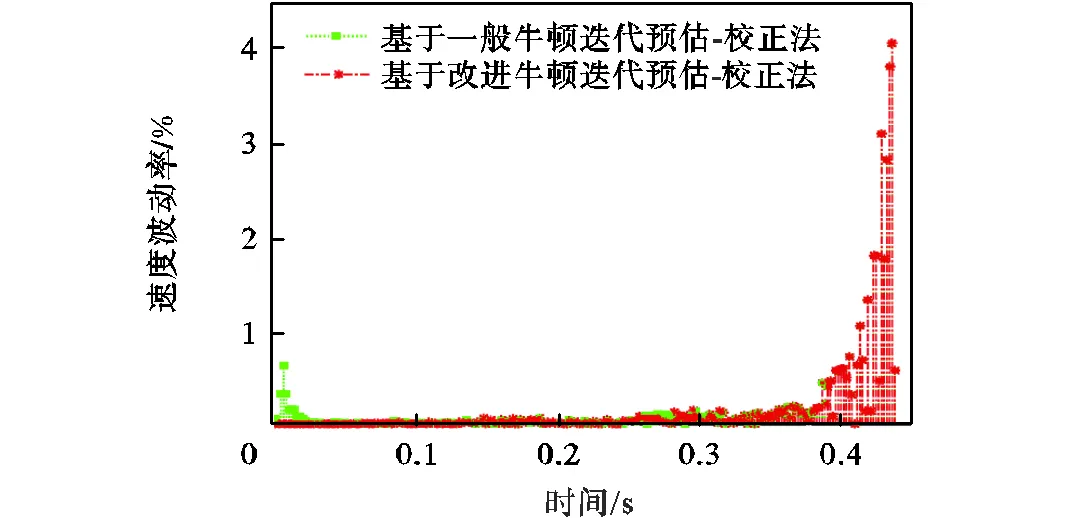
图13 两种预估-校正法的速度波动率对比

图14 2阶Runge-Kutta附加补偿值的方法与两种预估校正法计算耗时对比

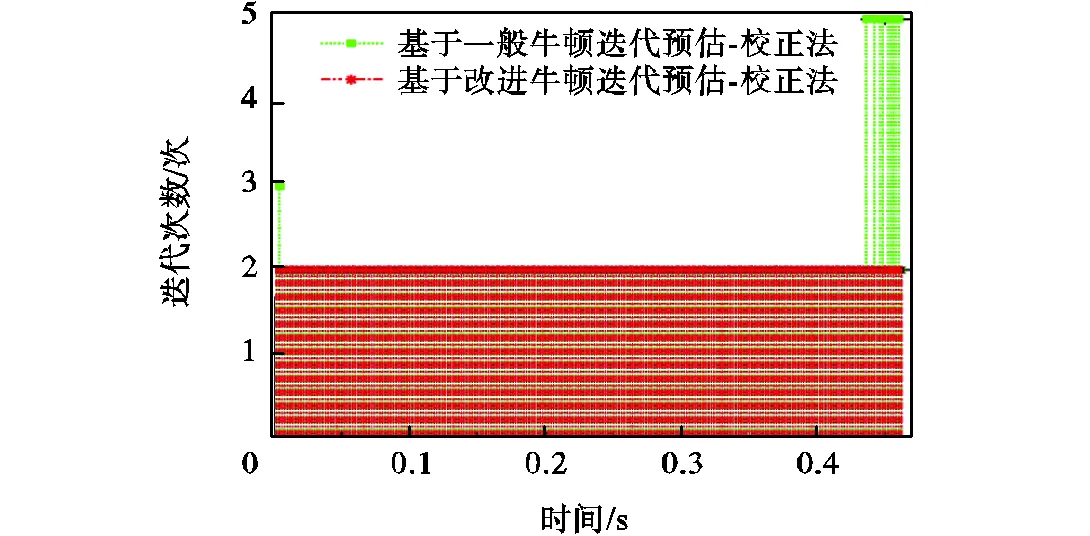
图15 两种预估-校正法迭代次数对比

6 实验验证

为进一步验证本文所提出的螺旋线插补算法的可行性，将该算法嵌入到本课题组开发的TSNC-SX-A1M型可重构数控系统中，在三轴铣床上进行切削加工实验．相关工艺要求如下：毛坯为6061铝板，刀具为6的两齿端面立铣刀，切削深度为0.4,mm，主轴转速为1,000,r/min，进给速度为600,mm/min．图16为加工所用机床与加工情况，待加工的螺旋线轨迹为＝10＋10/p(∈[0，3p])，如图17(a)所示，加工效果如图17(b)所示．实验结果表明，本文所提出的螺旋线插补算法可以在可重构数控系统平台上实现，算法有效且可行．

图16 加工机床与加工情况

图17 螺旋线实际加工

7 结 论

综上，通过对螺旋线数学方程的建立及其插补算法的研究，探究在曲率特性的持续限制下，尽可能得到合理的速度规划结果，同时提出了一种新的插补参数求解方法来进一步降低速度波动率，通过算法仿真分析与实验，得出以下结论：

(1) 速度规划算法在考虑曲率特性对运行速度的持续限制这一前提下，实现了螺旋线插补的柔性加减速控制；

(2) 与已有方法相比，基于改进牛顿迭代的预估-校正法在有效降低速度波动率的同时又具有较高的计算效率．

［1］ 张志强，王太勇，胡世广，等. 复杂空间参数曲线加工的插补算法[J]. 天津大学学报，2006，39(11)：1331-1335.

Zhang Zhiqiang，Wang Taiyong，Hu Shiguang，et al. Interpolation algorithm for machining complex parametric curves in space[J].，2006，39(11)：1331-1335(in Chinese).

［2］ 王爱玲，沈兴全，吴淑琴，等. 现代数控编程技术及应用[M]. 北京：国防工业出版社，2002.

Wang Ailing，Shen Xingquan，Wu Shuqin，et al.[M]. Beijing：National Defence Industry Press，2002(in Chinese).

［3］ 杨 萍，杨明泰，张阳阳. 高速数控加工中NURBS曲线拟合及插补技术的研究[J]. 中国机械工程，2015，26(12)：1630-1234.

Yang Ping，Yang Mingtai，Zhang Yangyang. Research on technologies of NURBS curve fitting and interpolation in high speed NC machining[J].，2015，26(12)：1630-1234(in Chinese).

［4］ 罗良玲，曹苏明. 基于时间分割法的阿基米德螺线的插补算法研究[J]. 南昌大学学报：工学版，2002，24(3)：22-24.

Luo Liangling，Cao Suming. The calculation of interpolation of spiral of archimedes based on time-divided method[J].：，2002，24(3)：22-24(in Chinese).

［5］ 刘 萍，梅晓妍，王民权. 变半径螺旋线插补铣削宏程序优化设计[J]. 组合机床与自动化加工技术，2014，3(3)：143-145.

Liu Ping，Mei Xiaoyan，Wang Mingquan. Optimization design of macro program for variable radius spiral interpolation milling[J].，2014，3(3)：143-145 (in Chinese).

［6］ 邵伟平. 内锥螺纹的数控铣削分析[J]. 制造技术与机床，2009(1)：24-25.

Shao Weiping. Numerical control milling analysis of inner cone thread [J].，2009(1)：24-25 (in Chinese).

［7］ 沈文华，张吉堂，于松章. 基于宏程序的阿基米德螺线形凸轮程序编制[J]. 机械管理开发，2016，31(3)：17-19.

Shen Wenhua，Zhang Jitang，Yu Songzhang. The preparation of archimedes spiral cam based on macro program[J].，2016，31(3)：17-19(in Chinese).

［8］ Qiu Hua，Akio Kubo，Li Ziye，et al. Optimal archimedes’ spiral interpolation for cutter path generation in NC machining of noncircular contours[J].，2008(36)：69-82.

［9］ Hu Ronghua，Liu Qiangfei，Song Honggun. Profile processing of scroll compressor and its error analysis[J].，2012，503/504：937-940.

［10］ 杨亮亮，许守金，史伟民，等. 始末速度不为零的S型加减速时间规划算法研究[J]. 机械工程学报，2016，52(23)：199-206.

Yang Liangliang，Xu Shoujin，Shi Weimin，et al. Research on S type acceleration and deceleration time planning algorithm with beginning and end speed non-zero[J].，2016，52(23)：199-206(in Chinese).

［11］ 富宏亚，李茂月，刘 源，等. 基于曲率特性的柔性加减速NURBS插补器[J]. 计算机集成制造系统，2012，18(9)：1921-1929.

Fu Hongya，Li Maoyue，Liu Yuan，et al. NURBS interpolator with flexible acceleration and deceleration based on curvature properties[J].，2012，18(9)：1921-1929(in Chinese).

［12］ 田军峰，林 浒，姚 壮，等. 数控系统S型曲线加减速快速规划研究[J]. 小型微型计算机系统，2013，34(1)：168-172.

Tian Junfeng，Lin Hu，Yao Zhuang，et al. Study on S-shape curve acceleration and deceleration control fast planning on CNC system[J].，2013，34(1)：168-172(in Chinese).

［13］ 刘 强，刘 焕，周胜凯，等. 无速度波动的NURBS曲线二次插补算法原理及其实现[J]. 计算机集成制造系统，2015，21(10)：2659-2667.

Liu Qiang，Liu Huan，Zhou Shengkai，et al. Principle and development of NURBS interpolation algorithm with zero-feedrate fluctuation[J].，2015，21(10)：2659-2667(in Chinese).

［14］ Jia Zhenyuan，Song Dening，Ma Jianwei，et al. A NURBS interpolator with constant speed at federate-sensitive regions under drive and contour-error constraints[J].，2017，116：1-17.

［15］ Wang Yunsen，Yang Dongsheng，Liu Yinzhong. A real-time look-ahead interpolation algorithm based on Akima curve fitting[J].，2014，85(5)：122-130.

［16］ Wang Guoxun，Shu Qinlin，Wang Jun，et al. Research on adaptive non-uniform rational B-spline real-time interpolation technology based on acceleration constraints [J].，2016，91(5)：1-12.

(责任编辑：金顺爱)

Spiral Interpolation Velocity Planning and Method of Solving Interpolation Parameters

Wang Taiyong，You Zhongtong，Xin Quanqi

(School of Mechanical Engineering，Tianjin University，Tianjin 300350，China)

This study aims to propose an Archimedes spiral interpolation algorithm based on curvature characteristics and 7-segment-S-type acceleration/deceleration. To obtain a reasonable velocity planning result，the constant limitation of the variable spiral radius and curvature characteristics related to the running velocity was considered in the velocity planning of this interpolation algorithm. To reduce the high rate of velocity fluctuation in the general method of solving interpolation parameters，a predictor-corrector method based on an improved Newton iteration was designed. The first-order Taylor expansion method was used to obtain the initial iteration value，and then the exact value was obtained by the improved Newton iteration. The advantages and application value of the predictor-corrector method are shown by simulation comparison and experiment. The method can effectively reduce the rate of velocity fluctuation and meet the real-time requirement of the computer numerical control(CNC)systems.

Archimedes spiral；acceleration/deceleration planning；velocity fluctuation；improved Newton iteration method

the National Natural Science Foundation of China(No.,51475324) and the Tianjin Science & Technology Council (No.,16PTGCCX00080).

TH164

A

0493-2137(2018)11-1107-10

10.11784/tdxbz201803042

2018-03-13；

2018-07-07.

王太勇（1962—  ），男，博士，教授，tywang@tju.edu.cn.

尤中桐，you_zhongtong@163.com.

国家自然科学基金资助项目(51475324)；天津市科学技术委员会资助项目(16PTGCCX00080).