基于气-砂两相流振动信号特征分析的砂粒检测

王 锴，张家林，刘 刚，李祎宸，王 刚，冯 凯



基于气-砂两相流振动信号特征分析的砂粒检测

王 锴1，张家林2，刘 刚1，李祎宸1，王 刚1，冯 凯1

(1. 中国石油大学(华东)石油工程学院，青岛 266580；2. 潍柴动力股份有限公司发动机技术研究院，潍坊 261000)

气-固两相流中固相信息的实时检测广泛应用于工业中的各个方面，特别是天然气开采过程中面临的出砂监测问题．为了丰富现有固相颗粒监测方法和技术，本文通过分析气-砂两相流流动撞击管壁激励的振动信号特征，开展气井出砂实时监测室内研究．本文利用加速度传感器感受砂粒撞击管壁的一次信号，随后通过信号调理、采集并转化为所需出砂信息．通过设计室内实验，对不同流速下的气流信号、不同携砂流速下的气-砂两相流信号、不同出砂率下的气-砂两相流信号进行时-频特征分析，结果表明14.0～18.0,kHz频段内气流信号幅值波动稳定且幅值较小，该频段为气井出砂监测的特征频段．进一步增加砂流量率，发现特征频段内的振动能量随含砂率的增加而增加，进一步验证了该出砂特征频段的有效性，并建立了气体流速与振动能量关系数学模型．本研究方法为后续较复杂的水-砂两相流、气-砂多相流流体中的固相检测研究奠定了良好的基础．

气-固两相流；振动信号；气井出砂；时-频分析

气-固两相流广泛存在于石油、核能、冶金和军工等各个行业，其中天然气开采、煤粉气力输送、浆料输送、粉末制备等过程检测均属于多相流中固相颗粒检测的范畴[1]．特别是在天然气开采的过程中，岩石层的细小砂粒伴随天然气进入生产管道[2]，产生管道出砂现象，砂粒进入管路后会造成管道的冲蚀，为安全的天然气生产埋下重大隐患[3-4]．由于多相流流动的力学特征及其复杂性，多相流中固相颗粒的检测一直是国内外研究人员探索的热点课题[5-8]．因此气-砂两相流中的砂粒在线检测对可靠的天然气生产管理、控制和运行具有重大意义．

近年来很多研究机构开展了多相流中的固相流动参数检测研究．Xu等[9]通过静电感应传感器发现了气动输送中的颗粒特性，该装置具有灵敏度高和结构简单等优点，但是体积较大，不适合天然气生产场所狭窄空间安装的要求．美国塔萨尔大学的Kesana等[10]采用电阻探针传感器获得了多相管流中的固相信息，该方法将探头植入管道内部，当含砂流体冲击探头时，传感器元件受到侵蚀，引起探头电阻值发生变化，从而得到砂粒含量信息，但是这种检测方式具有迟滞性，且植入安装需要改变管线生产流程，安装较为复杂．英国格拉摩根大学的Hii等[11]采用声发射技术检测了气固两相流中的颗粒参数特征，该系统将直径为1,mm的金属网垂直嵌入管道，声发射传感器以粘贴的方式安装在金属网上，当气-固两相流撞击金属网时产生声发射信号，随后经过处理得到多相流中的固相参数信息．综上所述，适用于气-砂两相流中砂粒的非植入式振动检测方法还鲜见报道．

本文提出了一种基于气-砂两相流动撞击弯管内壁激励振动信号特征分析的气井出砂检测系统和方法．该系统由加速度传感器、电荷放大器、信号采集装置、信号处理模块及分析软件组成．该方法将加速度传感器以非植入式的方法安装到下弯管管壁外侧，当气-砂两相流冲击管壁时，传感器探头感受到砂粒振动信号，经过采集处理后得到气-砂两相流中的砂粒流动参数信息．本文提出的气-砂两相流中砂粒检测方法具有安装方便、实时监测、体积较小和成本低等优势．

1 砂粒检测原理

气-砂两相管流以较高的速度经过弯头附近时，流体流向突变，砂粒在惯性的作用下摆脱流体拖拽力的束缚，撞击到管壁上并产生振动，如图1所示．同时砂粒对管壁做功产生冲击动能，检测该动能并将其转化为砂粒参数信息．其动能k为

 (1)

气流中砂粒撞击管壁产生微弱的非平稳振动信号，而传统的信号处理方法均基于静态假设，仅在时域或频域研究信号的统计特征，并不能揭示联合时-频平面内砂粒信号的时变特征．为了有效地区分砂粒冲击管壁与气流冲击管壁激励的信号特征[12]，同时弥补傅里叶变换在变换域内不能刻画信号特征的缺陷，本文采用基于短时傅里叶变换STFT的时-频分析方法对信号进行处理，该方法将一维时域分析转换为二维的时-频分析[13]，并展示信号的频域特征和能量特征，含砂流信号能量的幅值为

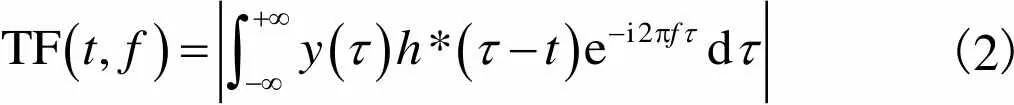
 (2)

采用带通滤波方法滤除出砂特征频段外的信号，进一步提取砂粒信号，滤波器的传递函数为

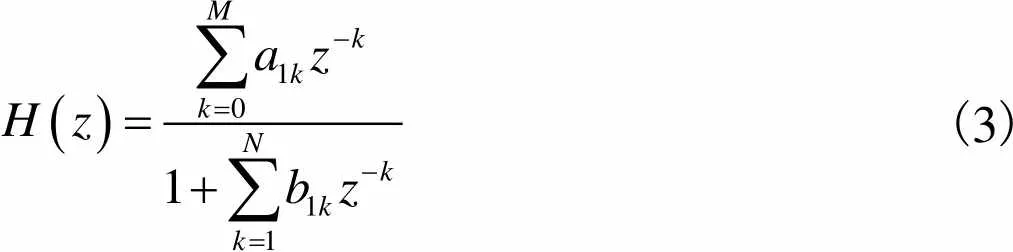
 (3)

多相流撞击管壁产生随机信号，对其自相关函数进行傅里叶变换得到自功率谱密度函数为

 (4)

两个随机信号的互功率谱密度函数为

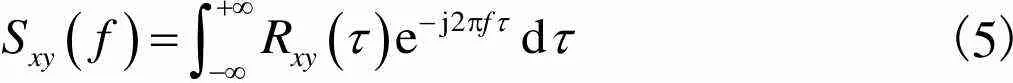
 (5)

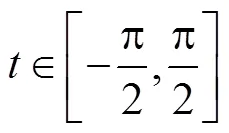
   (6)

2 实验装置和测试方法

2.1 实验装置

针对气-砂两相管流的流动特性，设计了室内模拟实验平台，如图2所示．该平台主要由供气系统、输气管路、加砂装置、数据采集处理设备、流量压力检测设备等组成．供气系统提供稳定气流，气体流入输运管道后，通过砂粒注入系统向管路中连续稳定地注入定量砂粒，气-砂混合充分发展后流经流量计、弯管等位置，最终流入砂粒收集装置．其中空气动力源由2,m3储气罐和0.86,MPa空气压缩机组成，系统采用ElektronikonII型电脑控制器对空气压缩机进行控制，为气-砂两相流输运提供稳定的流速．实验管路由304不锈钢制造，其中管线外径为34,mm、内径为25,mm，弯头曲率半径为2.5(为公称直径)．实验砂粒为石英砂，密度为2.65,g/cm3，莫氏硬度为7．

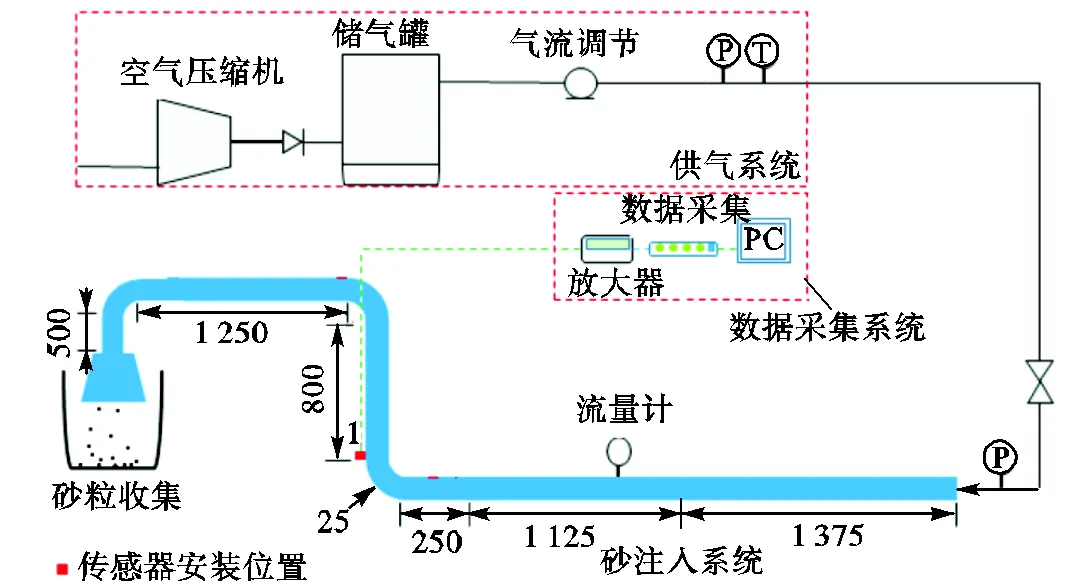
图2 气-砂两相流室内实验平台示意

采用PCB公司生产的357系列加速度传感器，实时获取含砂流撞击管壁激发的振动信号，如图2中编号1红点所示，传感器安装在下弯管外壁2～3倍管径处．随后含砂流撞击管壁产生的信号通过电缆传输至B&K 2692电荷放大器，转换为电压信号后通过B&K 3160数据采集模块进行采集．

2.2 实验设计

气-砂两相管流信号特征分析实验参数如表1所示，实验流程如下：

(1) 气流速度分别为2.5,m/s、3,m/s、3.5,m/s和4,m/s；

(2) 不同气流速度下砂粒粒径分别为45mm、75mm、106mm、150mm和180mm(325目、200目、150目、100目和80目)；

(3) 不同气流速度下砂流量率分别为0,g/s、0.2,g/s、0.4,g/s、0.6,g/s和0.8,g/s；

(4) 实验温度为10,℃．

3 实验结果分析

本文采用谱阵图分析方法对气-砂两相流非平稳随机振动信号展开分析研究．谱阵图将振动信号的能量随时间变化叠置为三维谱图，展现信号的频率随时间变化的关系，其能量幅值选用对数坐标，基本原理如图3所示．

表1 气-砂两相流实验参数

Tab.1 Test parameters of gas-sand two-phase flow

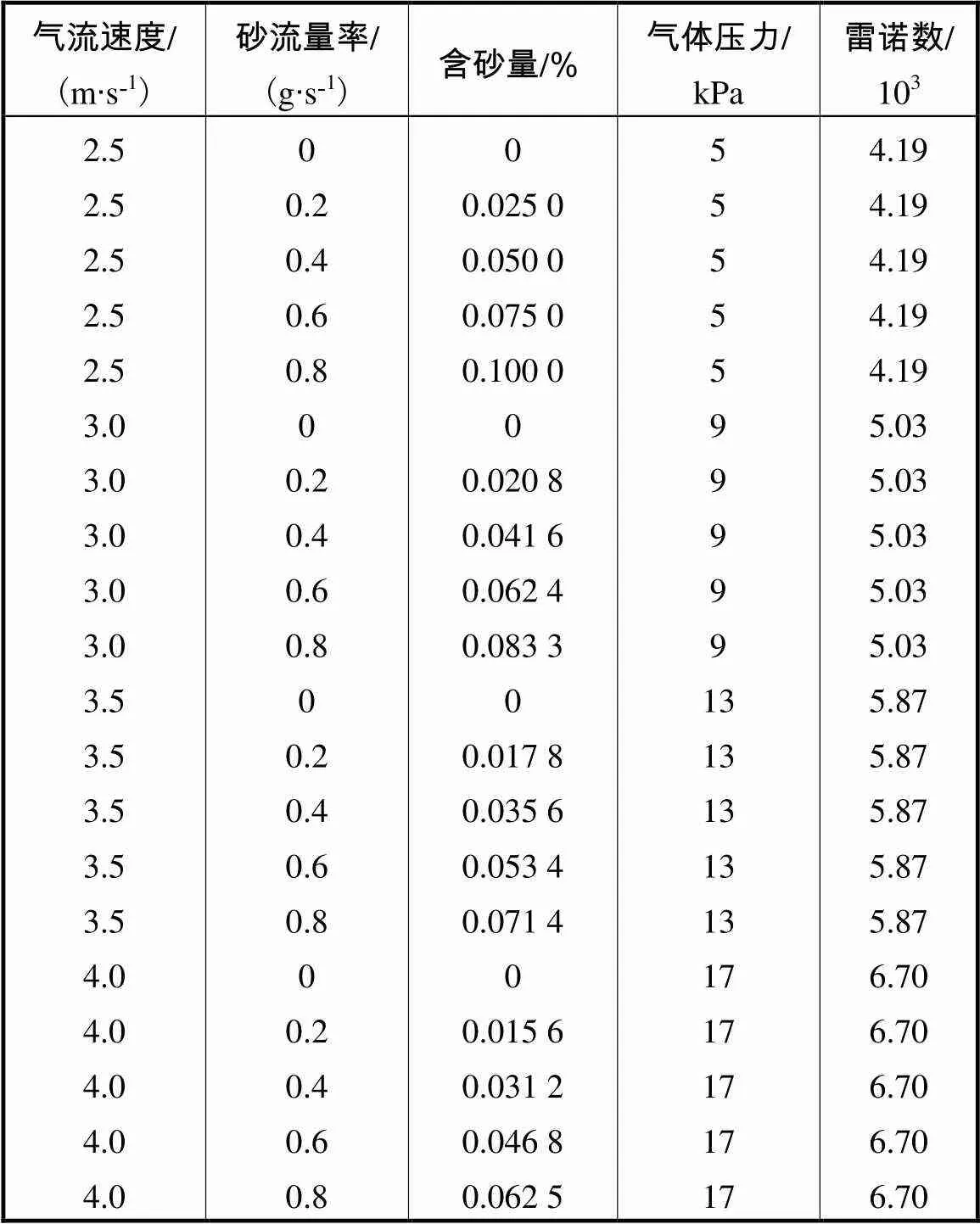
气流速度/(m·s-1)砂流量率/(g·s-1)含砂量/%,气体压力/kPa雷诺数/103 2.52.52.52.52.53.03.03.03.03.03.53.53.53.53.54.04.04.04.04.000.20.40.60.800.20.40.60.800.20.40.60.800.20.40.60.800.025,00.050,00.075,00.100,000.020,80.041,60.062,40.083,300.017,80.035,60.053,40.071,400.015,60.031,20.046,80.062,55555599999131313131317171717174.194.194.194.194.195.035.035.035.035.035.875.875.875.875.876.706.706.706.706.70

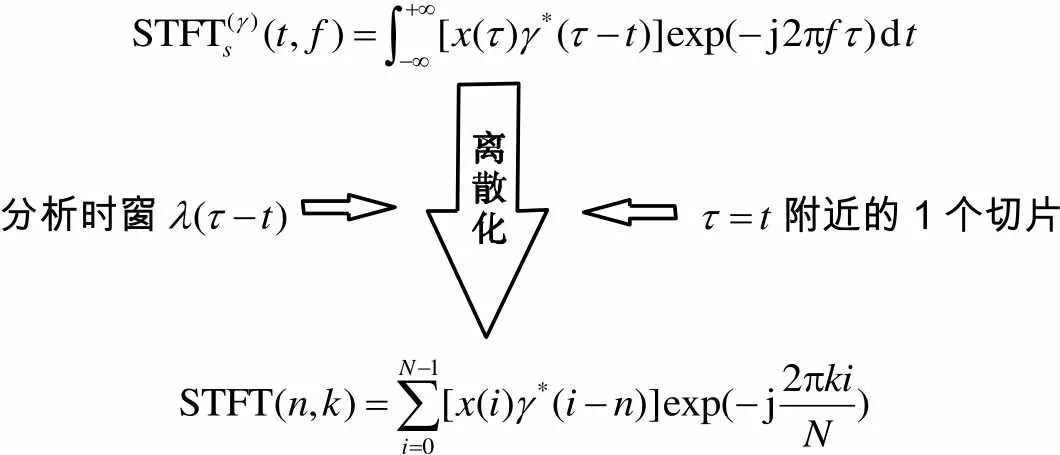
分析时窗附近的1个切片

图3 基于STFT的谱阵图分析原理

Fig.3 Principle of spectrum array analysis based on STFT

3.1 不同流速下的气流信号时-频特征分析

气-砂两相流冲击管壁产生的振动信号由气流产生的较强振动信号和砂粒产生的较弱振动信号组成．如图4所示，为不同流速下气流撞击管壁激励的振动信号，时域信号幅值随气流速度变化明显，因此流速对信号幅值的影响较大．为了提取含砂流中砂粒冲击管壁产生的弱振动信号，需要进一步分析气流冲击管壁产生的强振动信号特征．

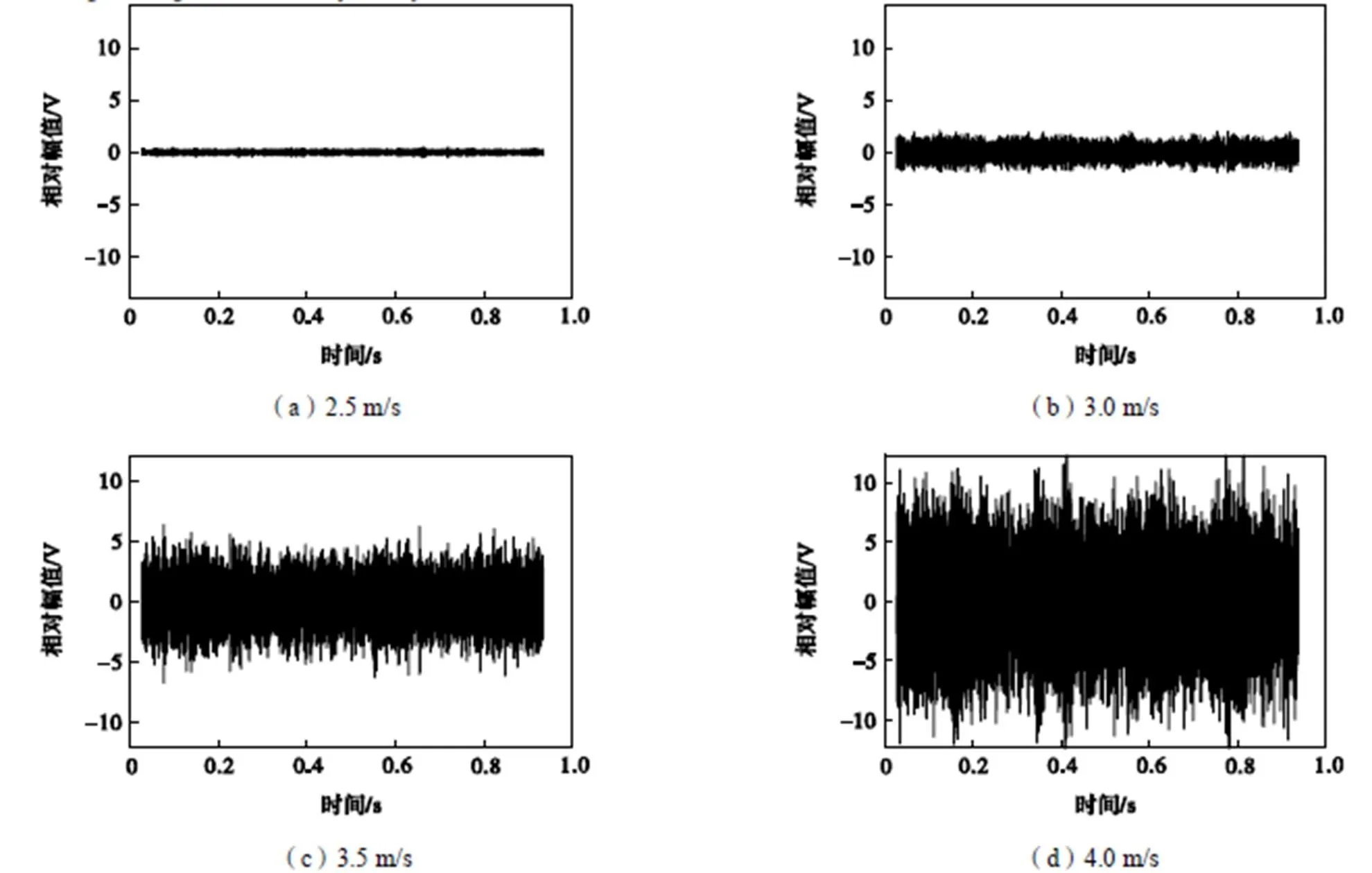
图4 不同流速下的气流信号时域特征

图5所示为不同流速下的频域特征，结果表明在6.5～8.5,kHz的主频率段，信号幅值随流速的变化明显，该频段为气流冲击管壁的主频段，即流速对信号的影响明显，因此不适合在该频段内寻找砂粒信号特征．

图5 不同流速下的气流信号频域分析结果

含砂流撞击管壁产生非平稳随机振动信号，而FFT分析仅表明频域区间内信号的统计特征，不能揭示联合时-频平面内气流信号的时变特征，因此选取STFT时频分析方法，进一步研究不同流速下，气流撞击管壁激发振动信号的时变能量特征．图6所示为一定时间内不同流速下气流振动信号的瀑布图分析结果，其中选取的窗口函数为Blackman，FFT长度为128个点．

从图6(a)中可以看出，流速为2.5,m/s时，气流产生的频域范围集中在6.5～8.5,kHz、11.0～12.5,kHz和14.0～18.0,kHz 3个频段．在6.5～8.5,kHz内，信号强度最高，且稳定性较好；在11.0～12.5,kHz内，信号强度次之，稳定性次之；在14.0～18.0,kHz内，信号强度最小，信号幅值微弱波动．因此2.5,m/s时的气流冲击管壁产生信号的特征频段为6.5～8.5,kHz．

图6(b)～(d)分析结果表明，流体速度为3.0,m/s、3.5,m/s和4.0,m/s时，气流冲击管壁产生信号的频率响应规律与图6(a)一致．

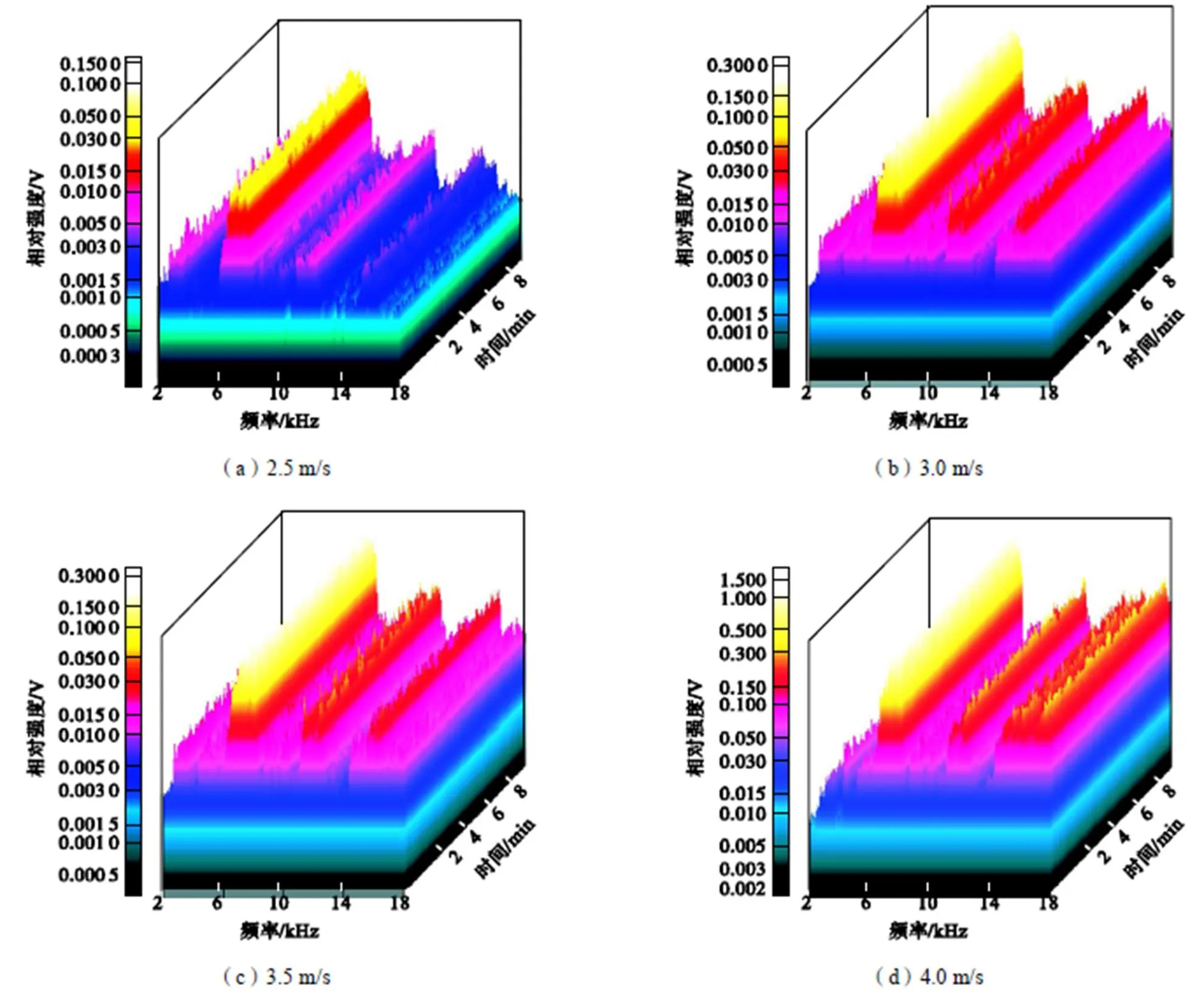
图6 不同流速下气流的谱阵图

3.2 不同流速下的含砂气流信号时-频特征分析

实验砂粒粒径较小，可忽略砂粒与气流的相对滑移速度，近似认为砂粒在管道中流动的速度等于气体在管道中流动的速度．对不同流速下、80目砂粒、0.2,g/s砂流量率的含砂气流进行频域分析，结果如图7所示．

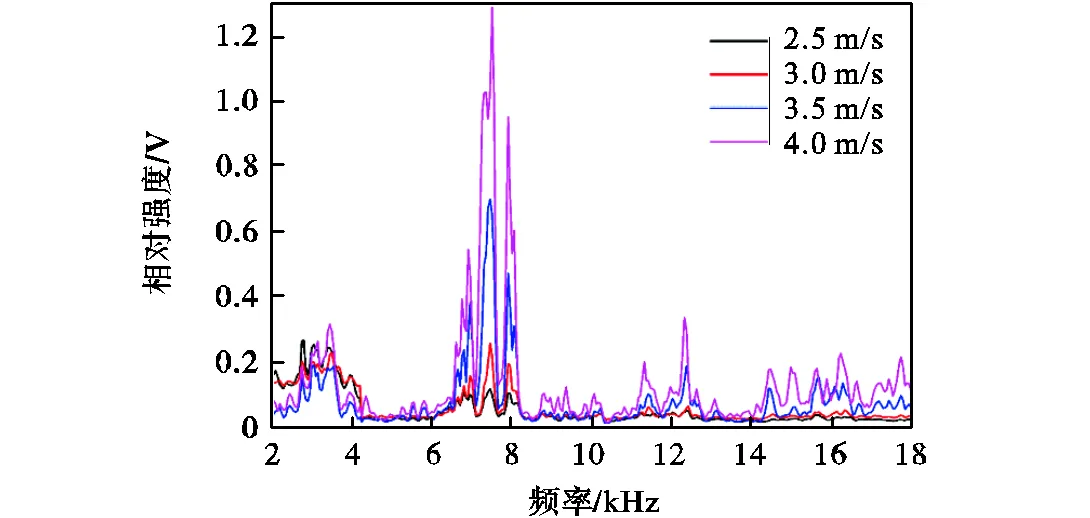
图7 不同流速下的气-砂两相流频域分析结果

由图7可知，在6.5～8.5,kHz频段内，信号幅值随流速变化明显，与图5中不同气体流速的频域分析结果对比，6.5～8.5,kHz频段内的信号幅值未发生明显变化，因此该频段为流体的敏感频段；砂粒冲击管壁的分析频段宜在10,kHz以上，且在14～18,kHz频段内，信号频域幅值变化明显，因此该频段为砂粒信号的特征频段．

采用相同的STFT时-频分析方法对气-砂两相流振动信号进行分析，图8所示为一定时间内气-砂两相流信号的瀑布图能量分析结果．

由图8(a)可知，气-砂两相流流速为2.5,m/s时产生振动信号的频率范围主要集中在6.5～8.5,kHz、11.0～12.5,kHz和14.0～18.0,kHz 3个频段．在6.5～8.5,kHz，信号强度最高，稳定性最好；在11.0～12.5,kHz，信号幅值强度有下降，信号的稳定性有所下降；在14.0～18.0,kHz内，信号幅值强度较11.0～12.5,kHz内信号有所提升，但明显看出信号幅值有波动．因此气流速度为2.5,m/s产生信号的主频段为6.5～8.5,kHz，波动最明显的频段为14～18,kHz．

图8 不同流速下气-砂两相流的谱阵图

图8(b)～(d)分析结果表明，流体速度为3.0,m/s、3.5,m/s和4.0,m/s时，气流冲击管壁产生信号的频率响应规律与图8(a)一致．

通过对比图6中气流信号的谱阵图分析结果和图8中气-砂两相流信号的谱阵图分析结果可知，气流含砂后，两相流冲击管壁产生振动信号的频段集中在6.5～8.5,kHz，但在14.0～18.0,kHz内，信号出现明显波动．因此在6.5～8.5,kHz频段内，砂粒冲击管壁的信号容易被淹没，必须选择更高的14.0～18.0,kHz作为砂粒信号特征频段．

3.3 不同出砂流量率下的含砂气流信号时-频分析

为了进一步研究不同砂流量率对气-砂两相流信号的影响，进行不同砂流量率下信号特征分析实验，选取砂粒粒径为150mm(100目)，携砂流流速为3.5,m/s．图9所示为不同砂流量率下的气-砂两相流频域信号分析结果，在6.5～8.5,kHz内，不同含砂量下的流体信号幅值变化不明显；11.0～12.5,kHz内，不同含砂量流体信号幅值有变化，但是规律不明显；14.0～18.0,kHz内，随着含砂量的增加，信号的幅值相应增加．因此，14.0～18.0,kHz可作为出砂特征频段．

图9 不同砂流量率下的气-砂两相流频域分析结果

3.4 气-砂两相流中砂粒信号与能量关系

在气-砂两相流的固相检测中，通过建立气-砂两相流中的砂流量率的数学模型验证文中振动检测方法的可靠性．气-砂两相流冲击管壁产生的振动能量用v表示，即

 (7)

为了降低气流噪声对砂粒信号特征识别的影响，进一步研究砂粒撞击外管壁产生的振动信号能量关系．通过对比不同流速下气流(图6)和含砂气流(图8)撞击管壁激励的振动信号特征，对砂粒冲击外管壁信号进行14.0～18.0,kHz内的带通滤波处理．图10所示为不同砂粒粒径、在不同速度下冲击外管壁产生的相对平均振动能量，其中平均振动能量为一定时间内信号电压值平方的积分，砂粒的粒径分别为45mm、75mm、106mm、150mm和180mm(325目、200目、150目、100目和80目)；砂粒冲击管壁的速度分别为2.5,m/s、3.0,m/s、3.5,m/s和4.0,m/s．结果表明，随着砂粒粒径的增加，砂粒冲击管壁产生的振动能量增加；随着砂粒冲击管壁速度的增加，砂粒冲击管壁产生的振动能量增加．

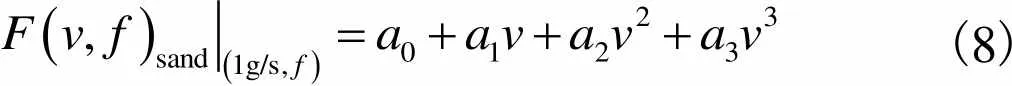
 (8)

对特征砂频段14.0～18.0,kHz内的信号进行滤波降噪处理，以获得不同条件下的气-砂两相流冲击管壁产生振动信号的相对平均振动能量．图11为不同砂粒粒径、不同砂流量下的气-砂两相流冲击内管壁产生的相对平均振动能量．

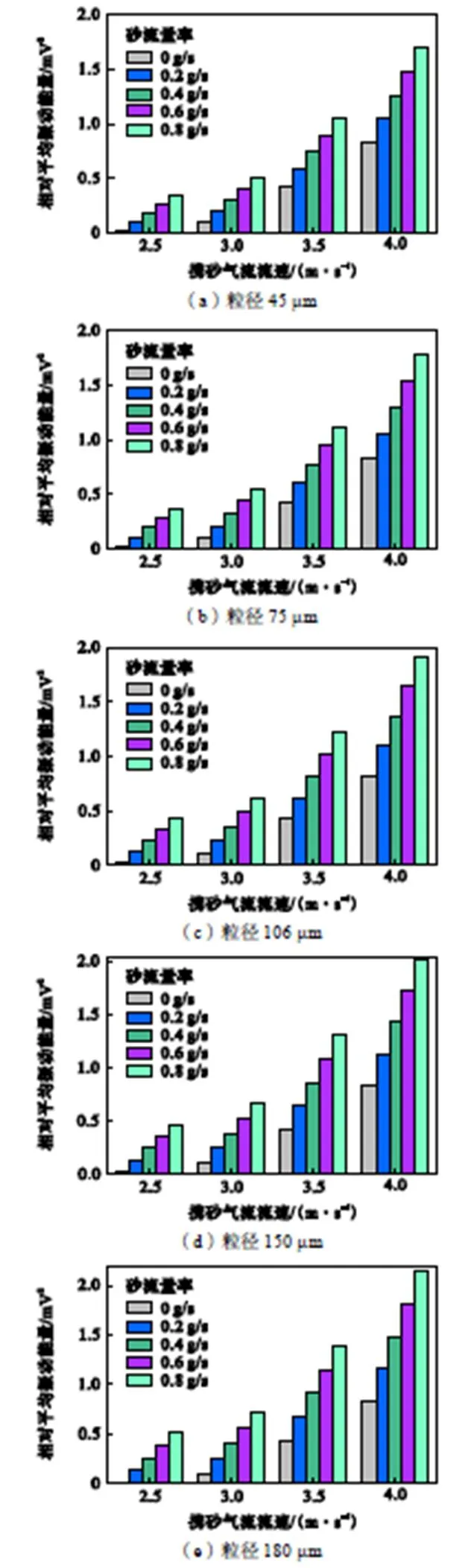
图11 不同流速和不同粒径下的砂粒冲击内管壁振动能量

如图11所示，砂流量率一定时，气-砂两相流冲击管壁产生的相对平均振动能量随着砂粒粒径的增加而增加；携砂流速一定时，气-砂两相流冲击管壁产生的相对平均振动能量随着砂粒粒径的增加而增加．不同流速的气流冲击管壁产生振动信号用3阶多项式描述，即

 (9)

将含砂率为零时不同流速下对应的振动平均能量代入式(9)，得到3阶多项式拟合系数，见表2．

用砂流量率评价气-砂两相流中的砂粒检测效果．气-砂两相流冲击管壁产生的振动信号经过处理转化为相应的振动能量．该振动能量可以描述砂流量率的趋势，但是为了获得较精确的砂流量率，需要对振动能量信号进行降噪处理，即将气-砂两相流冲击管壁产生的振动信号幅值减去该实验条件下气流冲击管壁产生的振动信号幅值．将经过降噪后的气-砂两相流信号除以参考校准砂信号，以定量分析并得到准确的砂流量率．参考校准砂信号即1,g/s砂流量率的砂粒冲击外管壁产生的振动信号，砂流量计算方法为

表2 式(9)中的系数

Tab.2 Parameters of Equation(9)

角标b相关系数平方值 01239.227,62-8.597,952.531,94-0.226,950.990.990.990.99

 (10)

利用式(10)对不同流速下气-砂两相流冲击管壁信号进行计算，以验证含砂率计算公式的准确性，其中砂粒粒径为75mm(200目)，每个流速进行4次实验．如图12所示，为式(10)计算后得到的砂流量率，砂流量率的计算值在理论值上下的10%,以内波动，结果表明该计算方法可以将不同流速、不同砂粒粒径条件对砂流量计算结果的影响弱化，且计算误差在10%,以内，因此采用振动方法可以对气-砂两相流中的砂粒含量进行定量检测．

图12 不同流体流速下的砂流量率

4 结 语

本文采用振动方法对气-砂两相流中的固相进行检测研究，通过分析不同流速下的气流信号、不同砂流速下的气-砂两相流信号、不同砂流量率下的气-砂两相流信号进行时频特征，结果表明在14～18,kHz的频段内气流信号幅值较小，且信号稳定，因此选取该频段为砂粒冲击管壁产生振动信号的特征频段，同时随着砂粒流速或质量的增加，特征频段内的信号幅值相应增加，再次验证了14～18,kHz内特征砂频段的有效性，并建立了气体流速与振动能量关系数学模型．该研究方法为后续较复杂的水-砂两相流、气-砂多相流流体中的固相检测研究奠定了良好的基础．

［1］ 田 昌，苏明旭，蔡小舒. 基于超声法测量气固两相流浓度实验研究[J]. 工程热物理学报，2013，34(8)：1487-1490.

Tian Chang，Su Mingxu，Cai Xiaoshu. Particle concentration characterization in gas-solid two-phase flow by ultrasonic methods[J].，2013，34(8)：1487-1490(in Chinese).

［2］ Ranjitha P G，Pereraa M S A，Pereraa W K G，et al. Sand production during the extrusion of hydrocarbons from geological formations：A review[J].，2014，124：72-82.

［3］ Wang Z，Tian H，Deng J，et al. Improving well productivity through sand control[J].，2006，28：59-63.

［4］ Bianco L，Halleck P. Mechanisms of arch instability and sand production in two-phase saturated poorly consolidated sandstones[C]//. Hague，Netherlands，2001：SPE-68932-MS.

［5］ Zhai L S，Jin N D，Gao Z K，et al. The ultrasonic measurement of high water volume fraction in dispersed oil-in-water flows[J].，2013，94：271-283.

［6］ 刘 刚，陈 超，韩金良，等. 液固两相流声发射检测系统设计及实验评价[J]. 振动与冲击，2012，31(22)：178-182.

Liu Gang，Chen Chao，Han Jinliang，et al. Acoustic emission device design and laboratory evaluation of fluid-solid two-phase flow[J].，2012，31(22)：178-182(in Chinese).

［7］ Zheng Y G，Liu Q. Review of techniques for the mass flow rate measurement of pneumatically conveyed solids[J].，2011，44：589-604.

［8］ Guo M，Yan Y，Hua Y H，et al. On-line measurement of the size distribution of particles in a gas-solid two-phase flow through acoustic sensing and advanced signal analysis[J].，2014，40：169-177.

［9］ Xu C L，Wang S M，Tang G H，et al. Sensing characteristics of electrostatic inductive sensor for flow parameters measurement of pneumatically conveyed particles[J].，2007，65：582-592.

［10］ Kesana N R，Throneberry J M，McLaury B S，et al. Effect of particle size and liquid viscosity on erosion in annular and slug flow[J].，2014，136：1.

［11］ Hii N C，Tan C K，Wilcox S J，et al. An investigation of the generation of acoustic emission from the flow of particulate solids in pipelines[J].，2013，243：120-129.

［12］ Wang K，Liu G，Wu J，et al. Acoustic sensor approaches for sand detection in sand-water two-phase flows[J].，2017，320：739-747.

［13］ He Q B，Wang J，Hu F，et al. Wayside acoustic diagnosis of defective train bearings based on signal resampling and information enhancement[J].，2013，332：5635-5649.

［14］ 崔明根，吴勃英，王德明，等. 数值分析原理[M]. 北京：科学出版社，2003.

Cui Minggen，Wu Boying，Wang Deming，et al.[M]. Beijing：Science Press，2003(in Chinese).

(责任编辑：金顺爱)

Vibration Signal Characteristics Analysis for Sand Detection in Gas-Sand Two-Phase Flow

Wang Kai1，Zhang Jialin2，Liu Gang1，Li Yichen1，Wang Gang1，Feng Kai1

(1. School of Petroleum Engineering，China University of Petroleum，Qingdao 266580，China；2. Engine Technology Research Institute，Weichai Power Co.，Ltd.，Weifang 261000，China)

Real-time detection of solid-phase information in gas-solid two-phase flow is widely used in industry，especially in sand production monitoring problems faced in natural gas exploitation. In order to enrich existing solid-phase particle monitoring methods and technologies，sand production of gas well in laboratory has been studied by analyzing the vibration signal characteristics of the gas-sand two-phase flow when the sand impinges on the pipe wall. The accelerometer was used to acquire the sand signals which then were converted to the sand production information by signal acquisition and conditioning. In this test，the time-frequency characteristics of vibration signals were analyzed under the condition of different velocities of gas flow，different sand-carrying velocities of gas-sand two-phase flow and different sand rates of gas-sand two-phase flow. The results show that the amplitudes of gas flow signals are steady within 14.0—18.0,kHz，which is the characteristic frequency band of sand production monitoring for gas well. With the increase of sand flow rate，the vibration energy also increases within the sand characteristic frequency band. Furthermore，the results verify the validity of the sand characteristic frequency band，and the relationship between the gas flow velocity and vibration energy is established. This research method lays a good foundation for the follow-up research on solid phase detection in the more complex water-sand two-phase flow and gas-sand multiphase flow.

gas-solid two-phase flow；vibration signal；sand production of gas well；time-frequency analysis

TE242

A

0493-2137(2018)11-1130-09

10.11784/tdxbz201803063

2018-03-20；

2018-04-16.

王 锴（1989—  ），男，博士，讲师.

王 锴，635511729@qq.com.

山东省自然科学基金资助项目(ZR2017BEE060)；中央高校基本科研业务费专项资金资助项目(17CX02011A)；国家重点基础研究发展计划(973计划)资助项目(2015CB251200)；中国石油大学人才引进项目(YJ201601077).

the National Natural Science Foundation of Shandong Province，China(No.,ZR2017BEE060)，the Fundamental Research Funds for the Central Universities of China(No.,17CX02011A)，the National Basic Research Program of China (No.,2015CB251200) and the Talent Introduction Program of China University of Petroleum(No.,YJ201601077).