复杂长竖井引水隧洞施工通风两相流模拟研究

刘 震，王晓玲，刘长欣，禹 旺，洪 坤



复杂长竖井引水隧洞施工通风两相流模拟研究

刘 震，王晓玲，刘长欣，禹 旺，洪 坤

(天津大学水利工程仿真与安全国家重点实验室，天津 300350)

复杂长竖井引水隧洞纵横交错的洞室布置和上下平洞间的大高差导致其通风散烟困难，然而施工通风效果的好坏直接影响工程施工进度和施工安全．现有引水隧洞施工通风两相流数值模拟研究多是针对单一隧洞或同平面的交叉隧洞，并且其网格独立性分析局限于通过单一经验公式验证．本研究首先提出综合考虑气固两相相互作用力和上下平洞大高差导致的压差作用影响的复杂长竖井引水隧洞施工通风三维非稳态欧拉两相流数学模型，并且通过与现场实验数据对比，验证了数学模型的可靠性；其次，采用偏斜度指标、速度变化百分比以及经验公式对网格独立性进行分析，得出合理的网格划分方案；最后，结合实际工程，模拟得出复杂长竖井引水隧洞施工通风过程中的风流结构分布和污染物(粉尘、CO)迁移变化规律，并基于模拟结果得出合理的通风散烟时间．

复杂长竖井引水隧洞；施工通风；欧拉两相流模型；风流场分布；污染物迁移

复杂长竖井引水隧洞纵横交错的洞室布置，立体交叉的施工作业以及上下平洞间的大高差导致其通风散烟困难．然而，施工通风作为复杂长竖井引水隧洞钻爆开挖循环中的重要一环，直接影响着工程的施工进度和人员的身体健康，因此对其施工通风两相流复杂过程进行深入研究具有重要意义．

目前对于带竖井布置的地下工程通风数值模拟研究主要集中在交通隧道、矿井隧道和水电地下工程等方面．对于交通隧道方面的研究主要针对已建成公路或铁路隧道的自然通风模拟[1-4]，未涉及气固两相间相互掺混影响的复杂施工通风过程．在矿井隧道两相流施工通风研究方面，Klemens等[5]建立二维数学模型，对某矿井隧道内的粉尘运移过程进行了模拟．Toraño等[6]对矿井掘进面两种不同通风方案进行了两相流模拟优选．Han等[7]采用两相流模型对矿井压入式通风过程的喷雾除尘效率进行了模拟研究．针对水电工程钻爆法开挖通风中的两相流模拟问题，张静等[8]对独头隧洞钻爆开挖后的通风过程进行了Euler两相流模拟．王晓玲等[9]和Liu等[10]建立了综合考虑风流和壁面热交换影响的欧拉拉格朗日两相流模型，对西南某深埋隧洞爆破后粉尘颗粒运动进行了模拟研究．洪坤等[11]采用三维欧拉两相流模型对某水电站地下厂房二层施工通风过程进行了模拟研究．王晓玲等[12]建立三维大涡拉格朗日模型，对某引水隧洞施工通风粉尘颗粒运移进行了两相流模拟研究．

综上所述，已有的引水隧洞施工通风两相流模拟研究多是针对单一隧洞或同平面的交叉隧洞，然而长竖井引水隧洞洞室布置纵横交错，竖井导井贯通后的钻爆扩挖过程产生大量的污染物不易排出，现有研究缺乏既能解释施工通风两相流复杂运动机理，又考虑上下平洞间大高差特点的复杂长竖井引水隧洞三维非稳态两相流紊流模型；此外，目前引水隧洞施工通风模拟研究多忽略了网格独立性分析，已有的分析局限于通过单一经验公式验证其网格独立性[13-15]，然而网格划分的合理性直接影响着长竖井引水隧洞施工通风数值模拟的可靠性和准确性．

针对上述问题，本研究进行了长竖井引水隧洞施工通风两相流模拟研究，首先，建立施工通风三维非稳态欧拉两相流紊流数学模型，在动量方程中考虑气固间相互作用力，在初始条件中考虑上下平洞间大高差导致的气压差的影响；其次，采用偏斜度指标对网格质量进行评价，再通过速度变化百分比和经验公式对网格独立性进行科学分析，得出兼顾计算精度和效率的网格划分方案；最后，结合实际工程，对长竖井施工通风过程进行两相流模拟，基于模拟结果得出了合理的通风散烟时间，为工程实际提供理论指导和技术支撑．

1 数学模型

本研究建立综合考虑气固相互作用和上下平洞大高差导致的压差作用影响的三维非稳态欧拉两相流模型，采用分散紊流模型对控制方程进行封闭．

1.1 控制方程

质量守恒方程[16]为

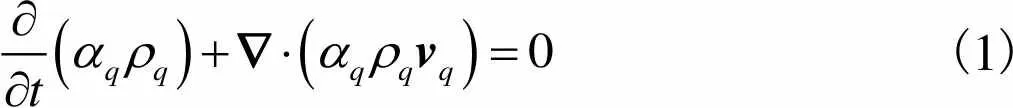
(1)

气相动量守恒方程为

(2)

固相动量守恒方程为

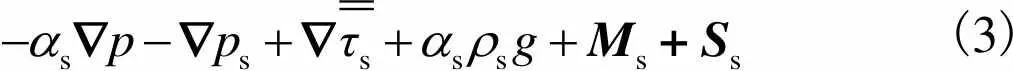
(3)

相间动量传递有相间曳力D、虚拟质量力VM和升力L，则传递项表达式为

(4)

1.2 紊流模型

采用分散紊流模型作为施工通风两相流模拟的紊流模型，分散紊流模型中主相紊流对第二相随机运动起决定作用．当数值模拟中有一个主连续相(空气)而其他是分散稀释的第二相(污染物)时，此模型是合适的[16].

(5)

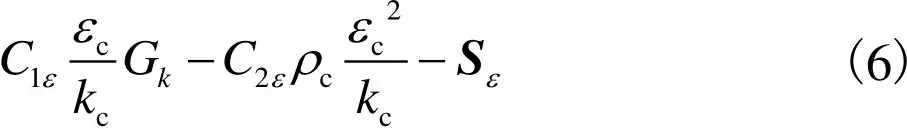
(6)

特征颗粒弛豫时间与作用于固相的惯性影响有关，将其定义[16]为

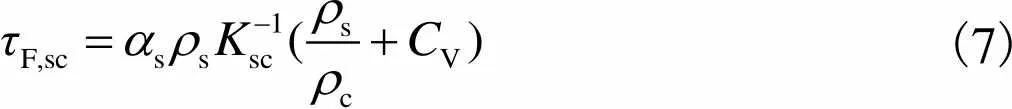
(7)

式中：sc为气固两相间交换系数；V为附加质量系数，取值为0.5．

Lagrangian积分时间标尺定义为

(8)

(9)

固相紊流量度可表示为

(10)

(11)

(12)

1.3 边界条件

假定流体为不可压缩瞬态流动，边界处的速度分布均匀，则各边界条件如下．

(2) 出口边界：采用压力出口边界条件，洞室出口与外界相通，出口处压力设为0，

(3) 固体壁面：长竖井引水隧洞内部壁面均设置为无滑移壁面边界，并且采用壁面函数经验公式处理近壁区的流动[17]．

1.4 初始条件

依据相关规范资料，地下工程钻爆发开挖时，产生大量有害气体和粉尘：主要有害气体是一氧化碳和氮的氧化物，在通风模拟中，将氮的氧化物按一定比例折算为一氧化碳[18]；爆破时粉尘浓度一般为300～500,mg/m3，对于引水隧洞的工程实际，取值为400,mg/m3[19-20]．

对于引水隧洞工程，上下平洞洞口间的高程差和隧洞内外的空气密度差决定了自然通风气压差的大小[21]，可表达为

(13)

则长竖井引水隧洞自然通风风量可表示为

(14)

式中：d为洞口流量系数；为洞口横截面积，m2；为引水隧洞内空气密度，kg/m3．

2 计算模型

2.1 物理模型

某长竖井引水隧洞长竖井段开挖时首先通过反井钻机将竖井贯通，形成一条竖井导井，再采用钻爆法自上而下对竖井进行扩挖，本研究以其钻爆扩挖施工通风过程为案例进行分析研究．图1为长竖井引水隧洞施工通风的几何模型，包括上下4条压力管道通过两条竖井相连通，上平洞压力管道通过M4施工支洞与外界连接，下平洞压力管道通过M1施工支洞以及进厂交通洞与外界相连接．两条竖井均长约500,m，圆形断面(见2-2断面图)，直径7.2,m；压力管道断面均为马蹄形(见1-1断面图)，面积约为56,m2．M4施工支洞洞口布置两台轴流风机，进厂交通洞布置一台轴流风机，使用风管沿着压力管道向竖井掌子面供风．

图1 长竖井引水隧洞施工通风几何模型

2.2 网格独立性分析

采用3种网格方案(A、B、C)对计算模型进行网格划分，各方案局部网格示意图见图2，网格总数分别约为310×104、580×104和1,090×104．

采用偏斜度指标EVS来评价所划分网格的质量好坏[22]，其表达式为

(15)

使用速度变化百分比(VPC)来比较使用不同网格时模拟结果的变化百分比，其计算公式为

表1 网格单元百分比与网格单元数量

Tab.1 Grid percentage and grid numbers

网格方案高质量网格单元百分比/%网格数量/104 A97.36310 B98.51580 C99.241,090

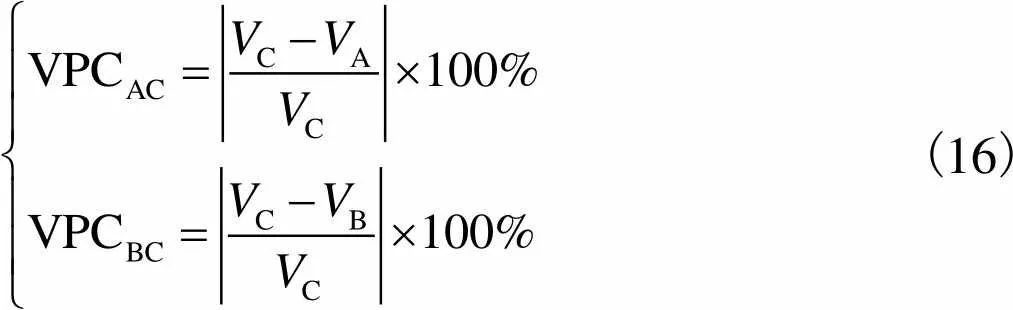
(16)

式中：VPCAC是网格方案A和网格方案C之间的速度变化百分比；VPCBC是网格方案B和网格方案C之间的速度变化百分比；V是速度模拟值，＝A， B，C．

对3种网格方案进行模拟，在射流轴线上距离风管出口5,m、10,m、15,m处取3个点，得出每个点的速度模拟值，计算VPC，具体结果见表2．

由表1和表2可知，由网格B到网格C网格数量大致加倍，B网格和网格C之间的流速变化低于2%,，因此认为网格独立性已经获得[23]．

式(17)是紊流射流轴心流速随射程变化的经验公式[24]，用来计算射流轴线上分别距离风管出口5,m、10,m、15,m处的流速，并与模拟值进行比较，计算结果见图3．

表2 VPC计算结果

Tab.2 Calculation results of VPC

到风管出口处距离/mVPCAC/%VPCBC/% 512.521.54 1015.851.76 1513.381.63

(17)

式中：是射流系数；是射程，m；0是受限贴附射流出口直径，m；0是出口流速，m/s．

通过与经验公式计算结果对比，网格方案C和网格方案B数值模拟结果的平均相对误差分别为4.74%,和6.31%,，网格方案A的模拟结果的平均相对误差是18.01%,．但网格方案C所需要的计算时间最长，故在兼顾可靠性和计算效率情况下，采用网格方案B．

图3 不同网格划分方案下的射流速度

2.3 模型验证

如图4所示，风管沿上平洞压力管道向竖井工作面供风．在一次爆破通风10,min后进行现场测试，共布置5个测点，分别为1、2、3、4和5，各测点之间相距10,m，测点位于断面中间，高度为1.5,m．表3为风流速度实验值和模拟值对比，由表可知，风流速度最大相对误差值为8.8%,，最小相对误差为2.8%,，平均相对误差为5.0%,，各测试点的模拟值与实验值之间呈现良好的一致性．

图4 现场实验测试点分布

表3 风流速度实测值与模拟值对比

Tab.3 Comparisonbetween measured and simulated values of airflow velocity

3 施工通风模拟结果与分析

3.1 风流场分析

图5为风流场基本稳定时长竖井引水隧洞风流矢量图．由图可知，当风流场基本稳定时，隧洞内风速满足施工洞最低风速要求0.15,m/s[25]．图6为压力管道与竖井连接处风流流线剖面图．综合图5和图6可知，由于隧洞内空间的限制，风流从风管射出后形成受限紊动射流，上平洞风管风流与竖井风流掺混后一部分向隧洞出口运动，另一部分在射流卷吸作用下，形成涡流区．下平洞风管风流受到隧洞壁面的影响改变运动方向，大部分风流进入竖井导井，少部分风流沿隧洞底部回流并被重新吸卷形成涡流区．

图5 风流场基本稳定时长竖井引水隧洞风流矢量图

图7为竖井导井内风流三个方向速度值曲线图．由图可知，在竖井导井内和方向速度值基本为0,m/s，方向速度值在竖井底部达到最大5.6,m/s，随后增大又减小并稳定在5.1,m/s左右．结合图5中区域放大图可知，在上下平洞大高差所导致的压差作用影响下，竖井导井内的风向为从下往上，整个长竖井引水隧洞内部整体风流的运动方向为沿着竖井向上并沿着上平洞压力管道向出口运动，即竖井掌子面爆破后的散烟方向为沿着竖井导井向上运动，经过压力管道由上平洞施工支洞排出．

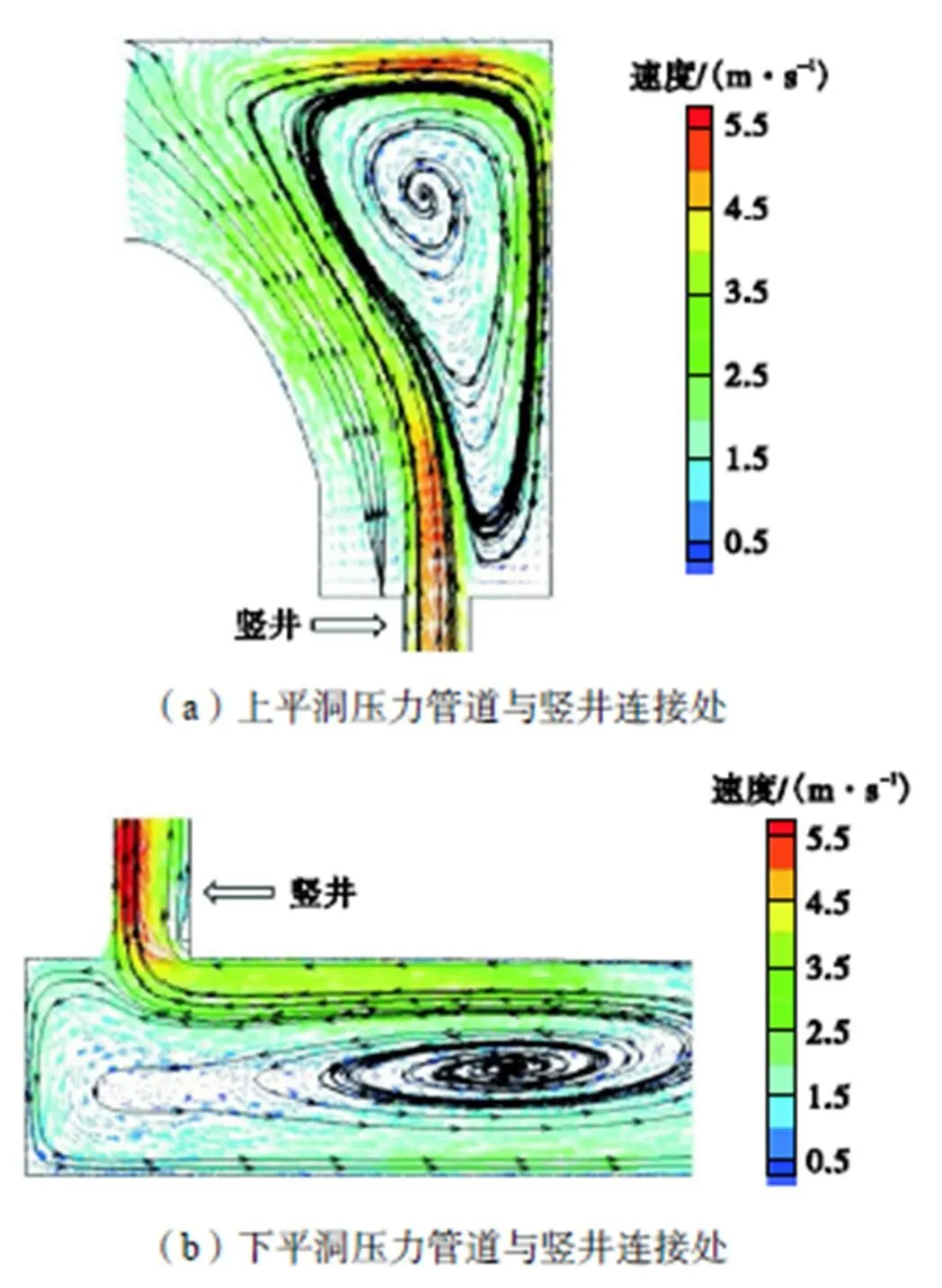
图6 压力管道与竖井连接处风流流线剖面

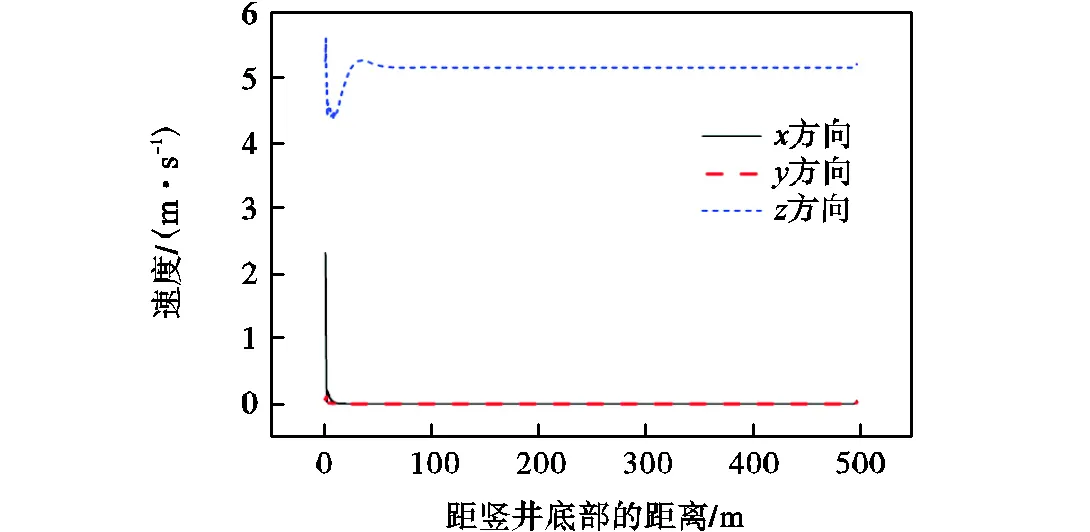
图7 竖井导井内各方向速度值

3.2 污染物运移分析

图8为施工通风45,s时工作面附近污染物(CO和粉尘)浓度分布等值线图．由图8(a)可知，通风45,s时，爆破产生的CO已经在风流的携带作用下，由竖井导井进入上平洞压力管道，此时在竖井和压力管道连接处形成一个高浓度区，这是因为此处存在风流涡流区(详见图6)，不利于排烟；另一个浓度聚集区是CO的主体部分，正沿着压力管道向出口运动，最大浓度为0.000,42(体积分数)．由图8(b)可知，通风45,s时，只有一个粉尘聚集区位于风流涡流区内，大部分粉尘还位于竖井和压力管道连接处，并且不断向压力管道内扩散运移，说明粉尘的扩散速度比CO慢．

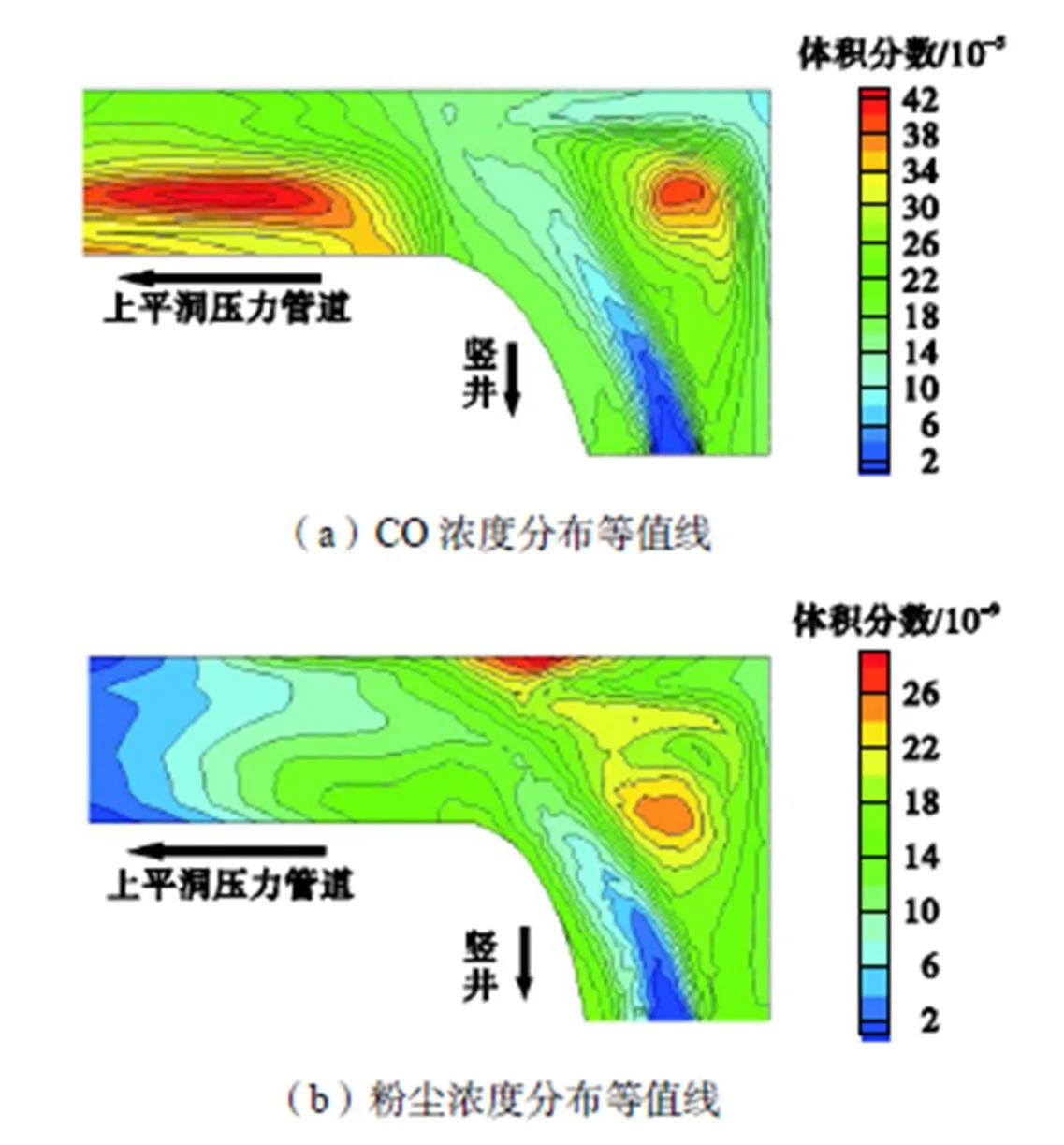
图8 通风45,s时工作面附近污染物浓度分布

图9 为不同通风时间下压力管道轴线处污染物浓度曲线．由图9可知，随着通风时间的增加，CO和粉尘在风流的携带作用下不断沿着上平洞压力管道向出口扩散运移；此外，由于风流的稀释和自身的扩散，CO和粉尘各时刻下的浓度最大值在不断下降，分布曲线在不断变扁平，此结论与陆茂成的现场实验结论一致[26]．通风240,s后，CO和粉尘浓度分布表现为类似正态分布，通风720,s左右，CO主体部分运移进入施工支洞M4，而粉尘由于物理性质不同运移较慢，在通风1,320,s左右才开始进入施工支洞M4．综合图8和图9可知，粉尘较CO而言在施工通风中更难被排除．

图10为长竖井引水隧洞内CO和粉尘浓度峰值随时间变化曲线．由图可知，在施工通风开始后，长竖井引水隧洞内CO和粉尘的峰值浓度均急剧下降，之后依然不断降低但是下降幅度减缓．依据相关规范，CO和粉尘浓度达标值分别为为30,mg/m3和2,mg/m3[25]，所对应的体积分数达标值分别为8×10-10,和2.4×10-5，所以爆破后长竖井引水隧洞内的CO浓度达标时间为1,790,s左右，粉尘浓度达标时间为2,340,s左右．因此基于粉尘浓度要求比CO严格以及粉尘较CO扩散运移缓慢又达标晚，本研究以粉尘浓度达标时间作为此工况下最终的施工通风时间，以满足引水隧洞内的通风要求．

图9 不同通风时间下压力管道轴线处污染物浓度曲线

图10 长竖井引水隧洞内污染物浓度峰值随时间变化曲线

4 结 语

针对复杂长竖井引水隧洞施工通风中因纵横交错的洞室布置和上下隧洞间大高差而导致的排烟困难问题，本研究提出了考虑复杂长竖井引水隧洞施工通风工程特点的欧拉两相流数学模型，并在对网格质量和网格独立性进行科学分析的基础上，采用所建立的数学模型对其施工通风过程进行了数值模拟研究．首先提出了综合考虑气固两相相互作用力和上下平洞大高差导致的压差作用影响的长竖井引水隧洞施工通风三维非稳态欧拉两相流数学模型，并采用现场实验数据对比验证了模型可靠性；其次采用偏斜度指标对网格质量进行了评价，采用速度变化百分比和经验公式对网格独立性进行了科学分析，得出了兼顾计算准确性和计算效率的网格划分方案；最后结合实际工程，对长竖井施工通风过程进行了两相流模拟，分析了洞室内的紊动射流和涡流区，得出了在上下平洞大高差所导致的压差作用影响下竖井导井内的风流方向；最后分析了爆破后随时间和空间变化的污染物(粉尘、CO)迁移变化规律，得出了污染物峰值浓度随时间变化曲线，并基于相关规范和模拟结果得出了合理的通风散烟时间．本研究的理论方法对于长竖井引水隧洞工程施工通风工程实际和模拟分析具有指导意义．

［1］ Ji J，Han J Y，Fan C G，et al. Influence of cross-sectional area and aspect ratio of shaft on natural ventilation in urban road tunnel[J].，2013，67：420-431.

［2］ Tong Y，Shi M H，Zhai Z Q. Smoke distribution in naturally ventilated urban transportation tunnels with multiple shafts[J].：，2013，29(3)：305-309.

［3］ Fan C G，Ji J，Wang W，et al. Effects of vertical shaft arrangement on natural ventilation performance during tunnel fires[J].，2014，73：158-169.

［4］ 童 艳，王昶舜，陈丽萍. 阻滞下的竖井型隧道自然通风试验与数值模拟[J]. 地下空间与工程学报，2015，11(1)：241-245.

Tong Yan，Wang Changshun，Chen Liping. Experiment and numerical simulation on natural ventilation for a traffic tunnel with shafts under traffic jam[J].，2015，11(1)：241-245(in Chinese).

［5］ Klemens R，Kosinski P，Wolanski P，et al. Numerical study of dust lifting in a channel with vertical obstacles [J].，2001，14(6)：469-473.

［6］ Toraño J，Torno S，Menendez M，et al. Auxiliary ventilation in mining roadways driven with roadheaders：Validated CFD modelling of dust behavior[J].，2011，26(1)：201-210.

［7］ Han F W，Wang D M，Jiang J X，et al. Modeling the influence of forced ventilation on the dispersion of droplets ejected from roadheader-mounted external sprayer [J].，2014，24(1)：129-135.

［8］ 张 静，王晓玲，陈红超，等. 引水隧洞独头掘进工作面风流和粉尘扩散的模拟[J]. 水力发电学报，2008，27(1)：111-117.

Zhang Jing，Wang Xiaoling，Chen Hongchao，et al. Simulation on ventilation and dust diffusion on heading face of the diversion tunnel[J].，2008，27(1)：111-117(in Chinese).

［9］ 王晓玲，刘 震，杨安林，等. 考虑热交换的引水隧洞施工通风两相流模拟[J]. 天津大学学报：自然科学与工程技术版，2013，46(4)：322-327.

Wang Xiaoling，Liu Zhen，Yang Anlin，et al. Simulation for construction ventilation two-phase flow in diversion tunnel considering heat exchange[J].：，2013，46(4)：322-327(in Chinese).

［10］ Liu Z，Wang X L，Cheng Z F，et al. Simulation of construction ventilation in long diversion tunnels using Euler-Lagrange method[J].，2014，105：28-38.

［11］ 洪 坤，刘 震，王晓玲，等. 水电站地下厂房钻爆施工工作面粉尘运移模拟[J]. 水力发电学报，2016，35(2)：124-130，

Hong Kun，Liu Zhen，Wang Xiaoling，et al. Simulation of dust migration at working faces during drill-blasting construction of underground hydropower houses[J].，2016，35(2)：124-130(in Chinese).

［12］ 王晓玲，朱泽彪，刘 震，等. 引水隧洞施工通风Euler-Lagrange两相流大涡模拟[J]. 天津大学学报：自然科学与工程技术版，2017，50(7)：725-731.

Wang Xiaoling，Zhu Zebiao，Liu Zhen，et al. Euler-Lagrange two-phase flow large eddy simulation of construction ventilation in diversion tunnel[J].：，2017，50(7)：725-731(in Chinese).

［13］ 张爱丽. 考虑热交换的大型深埋引水隧洞施工通风模拟[D]. 天津：天津大学建筑工程学院，2013.

Zhang Aili. Construction Ventilation Simulation in the Large-scale Deep Diversion Tunnel with Consideration of Heat Exchange[D]. Tianjin：School of Civil Engineering，Tianjin University，2013(in Chinese).

［14］ 曾 惜. 大型水电站地下洞室群施工期通风研究[D]. 成都：西南交通大学机械工程学院，2014.

Zeng Xi. Study on Construction Ventilation of Large Hydropower Station Underground Caverns[D]. Chengdu：School of Mechanical Engineering，Southwest Jiaotong University，2014(in Chinese).

［15］ 洪 坤. 复杂长竖井长距离引水隧洞施工进度风险分析与仿真优化研究[D]. 天津：天津大学管理与经济学院，2016.

Hong Kun. Schedule Risk Analysis and Simulation Optimization Research on Complex Long Distance Diversion Tunnel with Deep Shaft[D]. Tianjin：College of Management and Economics，Tianjin University，2016(in Chinese).

［16］ Fluent INC.6.3[M]. Lebanon：Fluent Documentation，2006.

［17］ Cebeci T，Bradshaw P.[M]. Washington：Hemisphere Publishing Corporation，1977.

［18］ 苏利军. 大型地下洞室群施工中的通风散烟问题研究[D]. 武汉：武汉水利电力大学水利水电学院，2000.

Su Lijun. Study on Ventilation and Smoke in Construction of Large Underground Caverns[D]. Wuhan：Wuhan University of Hydraulic and Electrical Engineering，2000(in Chinese).

［19］ 刘 毅，蒋仲安，蔡 卫，等. 综采工作面粉尘浓度分布的现场实测与数值模拟[J]. 煤炭科学技术，2006，34(4)：80-82.

Liu Yi，Jiang Zhongan，Cai Wei，et al. Site measurement and digital simulation of dust density distribution in

fully mechanized long wall coal mining face[J].，2006，34(4)：80-82(in Chinese).

［20］ 王晓珍，蒋仲安，刘 毅. 抽出式通风煤巷掘进过程中粉尘浓度分布规律的数值模拟[J]. 中国安全生产科学技术，2006，2(5)：24-28.

Wang Xiaozhen，Jiang Zhongan，Liu Yi. Numerical simulation of distribution regularities of dust concentration during the ventilation process of coal drift driving with exhaust ventilation[J].，2006，2(5)：24-28(in Chinese).

［21］ 杨立新. 现代隧道施工通风技术[M]. 北京：人民交通出版社，2012.

Yang Lixin.[M]. Beijing：China Communications Press，2012(in Chinese).

［22］ Fluent INC.2.4[M]. Lebanon：NH，2007.

［23］ Xu Guang. Remote Characterization of Underground Ventilation Systems Using Tracer Gas and CFD[D]. Blacksburg：Virginia Polytechnic Institute and State University，2013.

［24］ 伍悦滨，朱蒙生. 工程流体力学泵与风机[M]. 北京：化学工业出版社，2005.

Wu Yuebin，Zhu Mengsheng.[M]. Beijing：Chemical Industry Press，2005(in Chinese).

［25］ 水利电力部水利水电建设总局. 水利水电工程施工组织设计手册(第2卷)：施工技术[M]. 北京：水利电力出版社，1990.

Ministry of Water Resources and Electric Power Water Resources and Hydropower Construction Division.(Ⅱ)：[M]. Beijing：Water Conservancy and Electric Power Press，1990(in Chinese).

［26］ 杨立新，陆茂成. 隧道施工爆破后通风排烟风量计算的探讨[J]. 西部探矿工程，2000，62(1)：55-56.

Yang Lixin，Lu Maocheng. Discussion on calculation of ventilation and exhaust air volume after tunnel blasting [J].，2000，62(1)：55-56(in Chinese).

(责任编辑：王晓燕)

Two-Phase Flow Simulation of Construction Ventilation in the Complex Diversion Tunnels with Long Vertical Shafts

Liu Zhen，Wang Xiaoling，Liu Changxin，Yu Wang，Hong Kun

(State Key Laboratory of Hydraulic Engineering Simulation and Safety，Tianjin University，Tianjin 300350，China)

The crisscrossed cavity layout and large height difference between upper and lower horizontal sections in complex diversion tunnels with long vertical shafts result in difficulties in ventilation，and ventilation directly affects the construction schedule and safety．The current construction ventilation two-phase flow researches of diversion tunnel mainly focus on a single tunnel or conplane intersection tunnels，and the grid independence analysis is limited to single experience formula verification．Firstly，by considering gas-solid interaction force and pressure difference caused by large height difference between upper and lower horizontal sections synthetically，a three-dimensional unsteady Euler-Euler two-phase flow model was established，and the reliability of the mathematical model was verified by comparing it with in-situ test data．Then the equisize skew index，velocity percentage change and an experiential formula were used to analyze grid independence to obtain a reasonable meshing scheme．Finally，combined with practical engineering，the distribution of airflow structure and migration law of contaminants were obtained，and the rational ventilation time was proposed according to the simulation result.

complex diversion tunnels with long vertical shafts；construction ventilation；Euler-Euler two-phase flow model；airflow field distribution；contaminant transport

TK554

A

0493-2137(2018)11-1139-08

10.11784/tdxbz201801010

2018-01-02；

2018-02-08.

刘 震（1990—  ），男，博士研究生，tjuliuz@163.com.

王晓玲，wangxl@tju.edu.cn.

国家自然科学基金资助项目(51679165)；国家重点研发计划资助项目(2016YFC0401806)；国家自然科学基金创新群体资助项目(51621092).

the National Natural Science Foundation of China(No.,51679165)，National Key R&D Program of China(No.,2016YFC-0401806)and the Science Fund for Creative Research Groups of the National Natural Science Foundation of China (No.,51621092).