反舰弹道导弹一体化协同制导与控制
2018-11-08张聪
张 聪
(中国航天科工集团第四研究院指挥自动化技术研发与应用中心,北京 100854)
0 引 言
随着科技的发展,反导武器能力不断得到提升。为了增强弹道导弹的突防能力和生存能力,多弹协同攻击受到越来越多的关注。另外,弹间链技术进一步发展成熟,使多弹协同攻击成为可能。多弹协同可以通过弹间协同,将多枚导弹融合成一个信息共享、功能互补、战术协同的作战群体,利用群体优势对敌防御体系和目标进行多层次、全方位的打击,实现突防能力和打击能力的整体提升[1]。
对于协同问题,国内外在无人机编队协同制导与控制方面开展了大量理论和实物研究[2-4]。但因为导弹具有其特殊性,无人机的相关研究成果并不能直接应用于导弹的协同制导。本质上,导弹协同制导是多智能体协同制导与控制的一个方向,但导弹的速度更快、难以实现盘旋、静止等战术动作,所以要求其弹道应尽可能平直,这就对多导弹协同提出了更高的要求。
另外,与制导控制问题类似,现有协同制导研究中一般不考虑姿态控制环节或将姿态控制环节近似为一阶系统。这没有能充分考虑导弹机动性能的限制。鉴于此,本文在文献[5]的基础上,针对多反舰弹道导弹的末制导段,在领弹与从弹通信之外,加入从弹之间的相互通信,对一体化位姿控制进行拓展,提出一体化协同制导与控制的概念。以一致性理论为支撑,结合动态面控制和扩张状态观测器理论,研究“领弹—从弹”构型的多反舰弹道导弹的协同制导与控制问题。
定义1. 一体化协同制导与控制运用一体化思想[6-7]对多导弹的协同、制导、控制问题进行研究。
1 空间构型及数学模型
1.1 空间构型
本文研究主要针对多枚反舰弹道导弹齐射情景,进入末制导阶段后,各从弹以指定的空间位置跟随领弹,使其与领弹保持一定空间构型集中攻击同一目标。需要一枚有寻的制导能力的领弹对目标进行寻的攻击;其余从弹只需要其具有与其指定相邻从弹相互通信的能力,并要求至少有一枚从弹可以获取领弹信息。
1.2 数学模型
建立导弹的运动学和动力学模型、气动力和气动力矩模型、发动机模型。在气动力和气动力矩模型中加入扰动,模拟外界气流对导弹性能的影响[8-9]。
2 一体化协同制导与控制律设计
2.1 滚转通道独立设计
本文考虑导弹为轴对称气动外形,要求通过控制δx使速度倾斜角保持为0。因此,可将滚转通道独立出来进行控制算法设计。具体设计过程参见文献[5]。
2.2 多智能体形式的模型
文献[5]将力和力矩公式代入到运动学和动力学模型中,将滚转通道以外的其余通道整合为一体化位姿控制的设计模型,如下所示:
(1)
式中:

各变量具体含义详见文献[5]。
设有n枚从弹,则第i枚从弹的一体化协同制导与控制的多智能体形式的模型,如式(2)所示。各变量具体含义同文献[5]。
(2)
2.3 科学问题提炼
设计模型(2)的建立,将一体化协同制导与控制问题,提炼为针对如式(3)类型的高阶非线性多智能体系统,设计协同一致性算法的科学问题。
设有n个节点n>2,则第i个节点的状态方程表达式如式(3)所示。
(3)
式中:xil∈R是节点i的第l阶状态;fil(xi1,…,xi1):RM→R在定义域内Lipschitz连续,且fil(0,…,0)=0,是已知函数;ui∈R是控制输入;gil是放大系数;dil(t)∈R指本文所述的“总扰动”,未知且有界。这里的“总扰动”包含各种各样的扰动因素(如系统未建模部分、参数不确定性和外来干扰等)。
式(3)是串级系统,前k阶是积分型系统,后m-k阶中各阶都包含扰动项(非匹配扰动)。因此,针对第i个节点前k阶,基于一致性理论设计一致性算法,得到虚拟控制量xi(k+1)c;针对系统后m-k阶,需要在动态面控制的思想框架下,设计控制律使状态变量xi(k+1)迅速趋近虚拟控制量xi(k+1)c。
假设1. (a)对于前k阶,只有最外层状态xi1可以通过节点自身的传感器直接测量获取,其他状态需通过ESO进行估计;(b)后m-k阶中,各个状态量可通过节点自身传感器直接测量获得。
2.4 设计模型
本文中的领弹,可视为是多智能体系统中的主节点0,其时变动态可以描述为
(4)
式中:x0h∈R表示主节点的第h阶状态,h=1,…,k;x0:=x0,1,…,x0,k,f0(t,x0):[0,∞)×RM→R是分段局部Lipschitz连续的,f0(t,0,…,0)=0,且对于任意从节点是未知的。对于任意初始状态,t≥0时,系统(4)的解存在。主节点的动态(4)可以视为轨迹生成器。

定义节点i的第h阶跟踪误差为δih=xih-x0h,定义δh=[δ1h,…,δnh]T,则
δh=xh-x0,h
式中:x0,h=x0,h1,1=[1,…,1]T∈Rn,h=1,…,k。
本文目的是设计一体化协同制导与控制律,使跟踪误差δh(h=1,…,k)最终一致收敛到0的极小邻域内。以下定义具体描述了最终一致有界的概念。
定义2[10-11]. 协同最终一致有界:对于任意h(h=1,…,k),如果存在紧集Ωm⊂RN满足如下条件:
1){0}⊂Ωh
2)∀δh(t0)∈Ωh

则说跟踪误差δh是协同一致最终有界的(Cooperatively uniformly ultimately bounded, CUUB)。对于节点i,在t≥t0+Tm时,如果跟踪误差δh是协同一致最终有界的,则状态xih收敛到x0h的邻域内。
定义协同误差为
(5)
式中:bi≥0表示主节点0到从节点i的通信权重,当且仅当从节点i可以从主节点获取信息时bi>0。
定义eh=[e1h,…,enh]T,B=diag(b1,…,bn)∈Rn×n,f0=[f0(t,x0),…,f0(t,x0)]T∈Rn。由图论知识可得L1=0,其中,0=[0,…,0]T∈Rn,1=[1,…,1]T∈Rn,可以得到误差动态的向量形式,如下所示:
(6)
对式(6)求导可得协同误差的状态方程组形式
(7)
式中:fk=[f1k(xi),…,fnk(xi)]T,xk_=[x1k_,…,xnk_]T,Gk=diag(g1k,…,gnk)。
进一步,根据假设1(a),针对系统前k阶,只有最外层状态xi1可以通过节点自身的传感器直接测量获取,其他状态将通过ESO进行估计。因此,得到协同误差的估计量,如下
(8)
将式(8)整合成如下向量形式,
(9)
对式(8)求导可得估计协同误差的状态方程组形式
(10)

2.5 等效误差
定义误差si如下:
si=λ1ei1+…+λk-1ei(k-1)+eik
(11)
选取λ1,…,λk-1使多项式sk-1+λk-1sk-2+…+λ1是Hurwitz的。因此在误差面上(si=0),eih指数收敛到0,h=1,…,k。因此,控制误差si保持为0或在0附近,即可保证eih为0或是最终一致有界的。
误差的向量形式为s=[s1,…,sn]T∈Rn,则
s=λ1e1+…+λk-1ek-1+ek
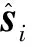

得到
(12)
由于λ1,…,λk-1使多项式sk-1+λk-1sk-2+…+λ1是Hurwitz的,所以Λ是Hurwitz的,对于给定的正数κ,存在整定矩阵PΛ,满足
ΛTPΛ+PΛΛ=-κI
(13)
则向量形式估计滑模误差的导数为
以下定理表明当si有界时,即有ei有界。因此只需确保si有界即可。即称si为ei的等效误差。
引理1[11-12].对于任意节点i,i=1,…,n,设
对于任意边界层ψi>0,ξi>0,任意时间Ti>t0存在边界Ψi>0, Ξi>0和时间Δi>t0,使得
2.6 一体化协同制导与控制律设计及分析
由于假设1,本节先设计扩张状态观测器,之后再设计一致性算法来解决系统的协同跟踪问题。
2.6.1扩张状态观测器设计
需要进行扩张状态观测器设计的原因有2个:1)在制导过程视线角速度信息较难获取,或需增加设计成本,通过观测手段可以低成本的获取视线角速度信息;2)模型中包含各种不同来源的干扰,需要通过观测手段对其进行估计,并在一体化制导控制回路中对其进行补偿以减少系统中的干扰,这有利于制导控制一体化回路的设计和整个系统的稳定性。扩张状态观测器无需区分误差类型和来源,可以对系统中的总体扰动进行实时估计,正好能满足以上2个需求。
式(3)相当于包含一个k阶积分型系统和m-k个一阶系统。所以,只需针对前k阶积分型系统进行扩张状态观测器的设计,也即包含了对后m-k的一阶系统的扩张状态观测器设计。
设k阶积分型系统如下
(14)
用扩张状态xk+1代替总扰动d(t),将式(14)扩张为k+1阶增广系统,如下所示:
(15)
针对式(15),设计ESO如下
(16)
写成状态方程组形式,如下所示:

(17)


选取ηh使得多项式sk+1+μ1sk+…+μks+μk+1是Hurwitz的,就有如下等式成立

(18)
式中:P,Q为正定矩阵。
对扩张状态观测器的稳定性和收敛性进行证明分析。设待选函数为
(19)
结合式(17)和式(18),求式(19)对时间的导数,有
(20)
结合P>0,从式(19)中可直接得出
整理得到
(21)
将式(21)代入式(20),得到
(22)
式(22)的解为
(23)
将式(23)代入式(21),得到
(24)

2.6.2前k阶算法设计


对从节点i设计分布式控制算法如下
(25)
写成向量形式为
(26)
适当地调整参数λ1,…,λk-1和c,分布式控制律(25)可以保证协同跟踪误差δh的最终一致有界。
下面将进行证明和分析。
在证明之前先引入如下引理和定理:
引理2[11-12].定义q=[q1,…,qN]T=(L+B)-11,P=diag{pi}=diag{1/qi},则矩阵P正定且存在正定矩阵Q使得
Q=P(L+B)+(L+B)TP
(27)
式中:1=[1,…,1]T。

定理1. 对于由从节点(3)和主节点(4)构成的多智能体系统。如果假设2成立,通过结合扩张状态观测器的分布式控制律(25)的控制,跟踪误差δ1,…,δM将协同一致最终有界。这意味着,图G中所有从节点的前k阶状态将在有界残差内同步趋近于主节点对应阶状态。
证. 取待选Lyapunov函数为
(28)
(29)

然后,结合式(12)和式(13),计算VE对时间的导数,可得
(30)

联合式(29)和式(30),整理得到
(31)
式中:
(32)

(33)
(34)
将式(32)代入式(28),得到
式中:Γ=diag(σmin(PΛ)/2,σmin(P)/2)
Τ=diag(σmax(PΛ)/2,σmax(P)/2)
通过文献[13]中的定理4.18得出结论:对于任意初始条件v(t0)存在时间T0,使得

(35)
结论1. 根据w的定义,式(35)即说明s是有限时间一致有界的,进而si是有限时间一致有界的。再根据引理1可知ei是有限时间一致有界的,进而eih是有限时间一致有界的。再根据定理 1得到δ1,…,δk是有限时间协同一致有界的,有向图G中的所有从节点的前k阶状态同步趋于主节点的对应阶状态。
2.6.3后m-k阶算法设计
由于系统后m-k阶相当于带有非匹配扰动的串级系统,所以考虑使用动态面控制的方法进行控制律的设计。下面对系统的后m-k阶进行算法设计和证明分析,这过程中将对假设sk+1和zk+1有界成立进行说明。
在系统的后m-k阶中,假设所有的状态变量可通过直接测量获得。扩张状态观测器的设计目的只是为了估计各阶总扰动。因此,设滑模面为
sil=xil-xild
(36)
结合式(3),求(36)对时间的导数如下
(37)
式中:zil=xild-xilc,l=k+1,…,m。
动态面控制律设计如下:
(38)
对系统后m-k阶的稳定性进行证明分析。设待选Lyapunov函数如下
(39)
结合式(37)和式(38),求取式(39)对时间的导数,得
0.5n(m-k)
(40)
式中:Δsil≥|gil||zi(l+1)|+|Δdil|∈R+,gim=0。
-2ζs(m-k)Vs(m-k)+0.5n(m-k)
(41)
再次,针对低通滤波部分进行稳定性证明。结合式(38)求zil对时间的导数如式(42)所示
(42)
设待选Lyapunov函数为
(43)
结合式(42),求取式(43)对时间的导数,得
0.5n(m-k)
(44)
(45)
然后,将Vs和Vz(m-k)部分进行整合。设待选Lyapunov函数为
Vsz=Vs+Vz(m-k)
(46)
整合式(41)和式(44),得到式(46)的导数为
Vz(m-k)+n(m-k)
(47)
设计ζz(m-k) (48) 式(48)的解为: 由结论1和结论2得出结论3。 结论3. 由控制律(25)和(38)构成的整体控制律,保证了由式(3)和式(4)构成的多智能体系统的有限时间协同一致有界。 针对本文“领弹—从弹”构型的多反舰弹道导弹系统给出具体的ICGC算法,如下 1)ESO 对于系统(2),需要一个3阶ESO和两个2阶ESO,如下 一个3阶ESO: (49) 两个2阶ESO分别为: (50) (51) 2)ICGC算法 ICGC算法如下所示 (52) 式中:ei1=xi1-xi1c,ei2=xi2-xi2c,i=1,2,3。 本节对一体化协同制导与控制算法进行仿真校验。即是对式(2)、(49)、(50)、(51)、(52)构成的闭环系统进行仿真校验。采用“领弹—从弹”的协同构型(其中包含1枚领弹和3枚从弹),各个从弹分别获取领弹位置速度信息,从弹之间相互通信,可获取其他从弹的位置速度信息。 为了突出本文算法的一致性特征,与文献[5]中的一体化位姿控制(Integrated control of position and attitude,ICPA)算法(53)进行对比。 (53) 关于“领弹—从弹”的协同构型采用图论拓扑的形式进行描述。具体针对以下两种拓扑结构进行仿真。其中,拓扑结构1,各个从弹分别获取领弹位置速度信息,从弹之间无通信;拓扑结构2,各个从弹分别获取领弹位置速度信息,从弹之间相互通信,可获取邻居从弹的位置速度信息。对应邻接矩阵A和主从矩阵B如表1所示。 表1 拓扑结构Table 1 Topological structure 当从弹间没有通信,且每个从弹都能从领弹获取信息时,有bi=1,di=0;令λ1=c1,λ2=1,K=c且式(53)中η=0。则式(52)与式(53)完全相同。即此时一体化协同制导与控制退化为一体化位姿控制。 期望空间构型如表2所示,领弹和各枚从弹的状态初始值如表3所示,算法参数设定如表4所示。本节的多弹协同攻击仿真中,领弹的一体化制导控制算法采用NTSMC_DSC方法[14]。 表2 期望空间构型Table 2 Desired special structure 表3 领弹和各枚从弹的状态初始值Table 3 Initial-states of the lead and the follow 仿真结果如图1~图4所示。对比图1和图2发现,使用ICGC算法时3枚从弹位置曲线走势更具有一致性。对比图3和图4发现,使用ICGC算法时3枚从弹位置关系曲线走势更具有一致性。一体化协同制导与控制通过增强从弹间的一致性,进一步提高了多导弹末制导段的协同攻击的能力。 表4 算法参数设定Table 4 Parameters of ICGC 为了更具一般地对本文提出的算法进行校验,进行蒙特卡洛仿真试验对脱靶量进行统计。改变目标初始位置、拉偏气动数据,进行200次的蒙特卡洛仿真试验,统计结果如表5所示。统计脱靶量的期望(μ)和均方差(σ)。发现在当前仿真场景中,领弹和从弹的脱靶量都很小。 表5 Monte Carlo仿真试验统计分析结果Table 5 Results and analysis of Monte-Carlo simulations 本文将一体化思想延伸到一体化协同制导与控制问题中。首先,将一体化协同制导与控制问题,提炼为针对一类型的高阶非线性多智能体系统,并设计协同一致性算法的科学问题。其次,设计了分布式一致性控制算法,对其稳定性和收敛特性进行了证明与分析,并取得了收敛条件。最后,通过ICGC和ICPA的仿真对比,突出了ICGC方法的一致性特性。另外,对于大机动性弹道,由于导弹自身结构和稳定性等需求对气动角进行了限制,仿真过程中系统出现了不同程度的饱和。这是期望攻击角度和气动角度限制之间的矛盾,如何解决这个矛盾可作为以后的研究方向。
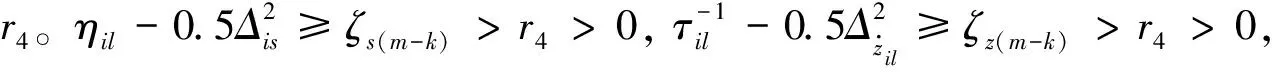
2.7 一体化协同制导与控制具体算法
3 仿真校验





4 结 论
