一种改进的航天器时变模态参数递推辨识方法

倪智宇，刘金国，吴志刚

(1. 中国科学院沈阳自动化研究所机器人学国家重点实验室，沈阳 110016； 2. 大连理工大学航空航天学院，大连 116024)

0 引 言

航天器系统模态参数的辨识实验目前已经在一些在轨空间结构上开展并获得成功，例如伽利略探测器、哈勃空间望远镜以及工程实验卫星(Engineering Test Satellite，ETS)系列等[1-3]，但这些在轨辨识实验均是基于定常系统模型进行的，比如ETS-VI卫星就在实验中将太阳能帆板固定在某一个角度，以防止它的旋转对整星模态参数辨识造成影响。从实际在轨运行的角度考虑，系统模态参数可能由于航天器的对接与分离、太阳能帆板的转动、大型天线的展开或者对目标物体的捕获等情况发生改变[4]。例如美国的土壤湿度主/被动观测卫星，携带的大型可展开式天线在工作时会始终以4 s/r的速度进行旋转[5]，而日本ETS-VIII卫星帆板的转动则可以导致结构参数的变化幅度高达25%[6]。可见这种由于结构构型改变而对系统模态参数造成的时变影响是不能够轻易忽略的，因此有必要考虑航天器运行过程中的时变模态参数辨识问题。

针对航天器的模态参数辨识问题，Juang等人[3]采用特征系统实现算法(Eigensystem Realization Algorithm，ERA)，使用控制力矩输入信号和陀螺仪量测信号的数据，对哈勃空间望远镜进行了结构频率和阻尼等模态参数的在轨辨识。黎康等人[7]仅利用被噪声污染的输入信号，基于子空间算法对挠性航天器的模态参数进行了辫识。Kasai等人[8]利用航天器姿态调整过程中的星体姿态信号和挠性附件振动响应信号，在ETS-VIII卫星上成功进行了系统模态参数的在轨辨识实验。文献[9]提出了一种基于视觉测量的太阳翼模态参数辨识方法，通过相机测量得到测点处的振动位移响应，然后采用ERA算法辨识太阳翼的模态参数。在现有的航天器模态参数辨识方法中，ERA和子空间方法是两种最为常用的时域辨识方法[10]。这两种方法的核心思想是通过构建相应的Hankel矩阵，利用奇异值分解(Singular Value Decomposition，SVD)计算得到系统的状态空间模型和对应的模态参数。这两种方法已经被工程人员证明是成熟可靠的辨识手段，但该类方法主要针对的是定常系统，对于时变系统的辨识能力极为有限。此外，对于航天器系统的控制问题而言，一些控制方法需要实时地获得系统的时变模态参数，以便于及时实现控制器参数的调整。因此有关航天器时变模态参数的辨识问题，寻找一种计算效率较快、更加适合于在线辨识的方法是有必要的[11]。

为克服基于SVD的子空间辨识方法计算效率较低的问题，Houtzager等人[12]提出了一种名叫基于递推预测器的子空间辨识(Recursive Predictor-Based Subspace Identification，RPBSID)方法。这种递推方法通过自适应滤波，利用外生向量自回归(Vector Autoregressive with Exogenous，VARX)预测器来提供渐进一致估计，从而通过求解最小二乘线性问题计算状态空间模型，进而辨识得到系统的时变模态参数。这类递推方法已经在一些机械和航空结构的辨识实验中得到验证，但是还尚未见到其在航天器参数辨识方面的应用研究。

本论文针对RPBSID方法在估计系统状态量时需要构建广义Hankel矩阵而导致数据量较大的问题，提出了一种改进后的RPBSID方法，并将其用于航天器时变模态参数的辨识中。这种改进方法通过引入仿射投影方法(Affine Projection Algorithm，APA)对状态量进行递推求解，不需要逐个时刻构建高维数的广义Hankel矩阵和进行矩阵求逆计算，从而提高了方法的计算效率。在数值算例中，建立带有大型挠性附件的卫星动力学模型，分别对线性变化、突然改变和周期变化三种情况下的系统模态频率进行辨识，辨识结果证明了这种递推方法能够有效地辨识得到航天器的时变模态频率值。通过与传统RPBSID方法计算结果的比较，证明本文提出的这种改进方法不仅能够保证计算的精度，而且具有更高的计算效率。

1 刚-挠耦合航天器的建模描述

对于常见的携带有太阳能帆板或者可展开式天线等附件的航天器结构，通常将其简化为中心刚体带有N个挠性附件的刚-挠耦合模型，因此这类航天器的动力学方程可以描述为[13]：

(1)

(2)

航天器在轨运行中，如果航天器的总质量或者结构构型发生变化，则会导致式(1)和(2)中的转动惯量矩阵J和耦合影响矩阵F是时变的。在这种情况下，我们首先定义一个状态矢量δ为：

(3)

那么，如果矩阵J和F是时变的，则式(1)和(2)可以表述为：

(4)

(5)

式中:I为单位阵。选择航天器的姿态信号ψ和附件的振动位移信号s作为m×1维的输出y(t)：

(6)

那么量测方程可以写为：

(7)

式中：

而C为m×n维的输出矩阵，Φ为相应的模态矩阵。

2 改进后的RPBSID方法辨识时变模态参数

2.1 Markov参数的递推估计

将式(5)和(7)进行离散化并考虑噪声对系统的影响，可以进一步将其写为如下的新息形式：

xk+1=Akxk+Bkuk+Kkek

(8)

yk=Ckxk+ek

(9)

式中：下标k为离散后的时间点，ek表示新息白噪声序列，而矩阵Kk表示卡尔曼增益矩阵。那么对式(8)和(9)做进一步的变换，可以写为：

(10)

yk=Ckxk+ek

(11)

定义一个如下形式的VARX预测器，则k时刻的输出yk可以表述为：

(12)

yk=Ξkφk

(13)

式中：

那么利用自适应滤波技术，可以得到各个采样时刻的矩阵Ξk的最小二乘递推形式为[12]：

(14)

(15)

式中：β1为遗忘因子，需要保证0<β1≤1；Zk为定义的临时变量矩阵，通常初值给为Z0=I。通过式(14)的递推计算，可以得到各个时刻的Markov参数矩阵Ξk的值，接下来将利用该参数矩阵Ξk递推估计系统的状态量xk。

2.2 基于仿射投影算法的系统状态量估计

在传统子空间方法中，状态量xk的计算通常基于SVD或QR分解；而原RPBSID方法在计算状态量时则需要分别构建各时刻的广义Hankel矩阵并对其中的参数矩阵进行求逆处理。上述方法往往均需要较大的计算量，为了减少辨识过程中的计算复杂度，本文这里拟采用递推形式来估计各个采样时刻的状态量xk。

对于式(10)-(11)，如果暂不考虑量测噪声ek，那么从k-p到k时刻的输出信号{yk-p,yk-p+1,…,yk}可以分别写为：

yk-p=Ck-pxk-p

(16)

(17)

(18)

则式(16)-(18)可以用矩阵形式表示为：

(19)

式中：

τk-p=Γk-pxk-p

(20)

那么对于k-1时刻，式(20)可以表示为如下的最小二乘形式：

τk-1=Γk-1xk-1

(21)

其中

(22)

对于式(21)，这里引入APA算法[15]，从而得到各个时刻状态量xk的递推形式为：

(23)

Φk-1=τk-1-Γk-1xk-1

(24)

式中：μ为递推过程中的仿射投影因子，一般应满足0<μ≪1。在式(23)的递推迭代中，矩阵Γk-1的初值Γ0应保证为满秩矩阵，如果没有其它先验知识，则Γ0一般可以选择为：

(25)

在式(23)中，在递推得到xk后，矩阵Γk的更新同样可以通过如下的递推最小二乘算法得到：

(26)

(27)

Γk=Γk-1+(τk-Γk-1xk)Wk

(28)

式中：β2为遗忘因子，而矩阵Lk的初值选取方式和Γ0相似。根据式(23)-(28)，可以递推计算得到各个时刻的状态量xk。

2.3 时变状态空间模型参数的递推估计

在得到系统的状态量xk后，则可以递推计算各个时刻的状态空间模型参数[Ak,Bk,Ck]。首先将式(8)和(9)重写为如下形式：

(29)

(30)

(31)

(32)

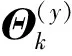
(33)

(34)

式中：矩阵Δk的初值Δ0的选取需要满足Δ0=(1/α1)I,α1>0。而式(30)中的新息噪音序列ek可以通过下式得到：

(35)

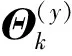
(36)

(37)

辨识得到系统矩阵Ak后，可以利用伪模态分析理论计算得到航天器的时变模态参数。对系统矩阵进行特征根分解计算：

(38)

Φk=CkΛk

(39)

2.4 改进的RPBSID方法与原算法计算复杂度比较

改进后的RPBSID方法的计算步骤可以简要地总结如下：

步骤1.通过式(14)和(15)，求解系统的Markov参数矩阵Ξk的值；

步骤2.根据式(22)-(24)以及(26)-(28)，计算得到状态量xk；

步骤4.利用式(38)和(39)计算得到航天器的时变模态参数。

本文对于原方法的改进主要集中在对状态量xk的递推估计，即步骤2。在递推过程中，由于参数p、r和m通常是选定好的，因此总的计算复杂度主要由系统的未知阶次数目n来决定，通过算法复杂度的估计可知，系统的最高计算复杂度为O(n2)。而原方法由于需要计算求逆估计状态量xk，因此其计算复杂度可以达到O(n3)。原方法计算状态量的内容请参见文献[12]，这里限于篇幅不再详述。此外，由于改进的递推方法不需要构造高维数的Hankel矩阵，从而减少了所需的数据量，这种计算优势在系统阶次较高时将更加明显，接下来将通过数值计算来证明。

3 仿真校验

在数值仿真中，选择带有大型挠性附件的ETS-VIII卫星作为建模对象，考虑当系统的模态参数值分别发生线性改变、突变和周期变化的情况，利用改进的递推方法辨识系统的时变模态频率值。

3.1 ETS-VIII卫星模型描述

ETS-VIII卫星携带一对大型可展开式天线反射器和一对太阳能帆板，是一个典型的刚-挠耦合航天器结构。对该卫星模型做如下的简化：将所携带的大型天线反射器和卫星主体部分分别简化为平面桁架和长方体结构，太阳能帆板和天线反射器通过连杆铰接于卫星中心体上，并且认为是由均质材料所组成。由于卫星在地球同步轨道上运行，因此这里忽略重力梯度的影响。全局坐标系的原点建立在整星的质心上，而附件坐标系的原点则建立在中心体与附件的铰接点上。简化后的卫星模型如图1所示，其中符号{s1,s2,a1,a2}分别表示该卫星的两副帆板s1/s2和两副天线反射器a1/a2。

图1 简化后的ETS-VIII模型Fig.1 Simplified ETS-VIII model

在仿真中，太阳能帆板s1/s2和天线a1/a2的频率可以通过有限元建模得到，而附件的阻尼比ζs1=ζs2=ζa1=ζa2=0.01。在建立动力学方程的过程中，选取每个附件的前3阶频率，因此该卫星模型的系统阶次为n=(3+4×3)×2=30。

3.2 时变模态频率的辨识

仿真条件中给定噪声的信噪比(Signal Noise Ratio，SNR)为40 dB，而辨识方法中的仿真参数如下：分块矩阵的参数p=15，递推系数α1,2=0.9、μ=0.05，遗忘因子β1,2,3,4=0.98，系统的采样时间Δt=0.1 s。分别考虑以下三种工况的时变频率辨识问题：

工况1：模态参数线性变化的情况

在该工况中，假设卫星的推进剂消耗导致结构整体质量发生线性改变的情况。当然，实际工作中，不同于运载火箭在发射阶段燃料迅速减少的情况，在卫星在轨过程中，推进剂的消耗是比较小而且非连续的。但在本算例中，为直观地表现出这种变化，假设在运行的过程中，卫星所携带的推进剂是较为快速且连续性的随着时间而不断消耗，基于这种假设，卫星中心刚体的质量(定义为mr)有着如下的线性变化关系：

mr2=mr1-ρtp

(40)

式中：mr1和mr2分别为卫星中心刚体在推进剂消耗前和消耗后的质量，而ρ为推进剂的消耗率，tp则是运行的时间。在仿真中给定mr1=2400 kg。给定推进剂的消耗率ρ=0.2 kg/s。由于系统质量的不断减少，从而导致某些阶次的系统频率发生时变变化。利用本文提出的改进RPBSID方法对这种工况下的结构模态参数进行辨识。从动力学方程(4)中可以看出，由于该方程包含有卫星的姿态运动方程(1)和各个附件的振动方程(2)，而式(1)中三个方向的姿态运动对应的模态参数值为零，所以在动力学方程(1)中，卫星的前三阶频率表征的是系统的刚体模态从而对应的值为零。此外，在动力学方程(1)-(4)中，由于转动惯量矩阵J(t)中的质量参数mr发生了变化(具体的转动惯量计算表达式请参见文献[6])，那么从质量和矢径矩阵的乘积中可以看出，转动惯量矩阵中只有部分元素发生了变化，从而导致只有部分阶次的模态参数随着质量变化而发生改变。对于本算例建立的卫星动力学模型，在前15阶系统频率中，只有第5、7、9和11阶的模态参数随着质量变化而改变，而其它阶次的频率、阻尼和振型参数仍为常值。

利用式(38)-(39)，计算得到系统的时变频率、阻尼比和模态振型。原RPBSID方法和改进后的递推方法对于这四阶时变频率的辨识结果如图2所示。值得注意的是，由于这类递推方法需要一个迭代逼近的过程，所以初始时刻的辨识值是有较大误差的，而图2只给出了系统在基本达到稳定跟踪后的辨识结果。表1则给出了这两种方法对于时变频率值和阻尼比的平均相对误差结果，其中RPBSID和改进后的递推方法均需要一个迭代过程来逼近模型的原始值，因此计算的是50 s-120 s区间内已达到稳定跟踪时的频率和阻尼比的平均相对误差值。计算结果证明这两种方法均能够有效地辨识线性时变系统的频率值，对于该算例，模态频率的最大误差不超过3%，但阻尼比的辨识结果则存在着较大的误差。这是由于阻尼分析的机理比较复杂，而且阻尼比还容易受到频率或者刚度的影响，特别是当含有噪声干扰时，噪声对于阻尼比辨识结果的影响要远大于对频率的影响，因此阻尼比往往难于准确辨识得到。

图2 两种方法辨识得到的系统时变频率值Fig.2 Identification results of system time-varying frequencies with two methods

表1 两种方法所得到的频率和阻尼比的平均相对误差Table 1 Average relative errors of frequencies and damping ratios for two methods

对于模态振型的辨识结果，这里通过引入模态置信准则(Modal Assurance Criteria，MAC)，来判断和比较原振型向量与辨识得到的振型之间的相似度。模态振型向量的MAC计算公式如下：

(41)

表2 两种方法所得到的时变模态振型的MAC值(t=80 s)Table 2 MAC values of mode shape for two methods (t=80 s)

工况2：模态参数突然变化的情况

在工况2中，模拟空间对接的情况，考虑卫星的中心刚体在Z轴(偏航轴)的两端分别与两个长方体结构对接的情况，如图3所示。在本仿真中，我们假设与其分别对接的两个长方体结构的尺寸均为2.35 m×2.45 m×3 m，质量均为600 kg，而卫星中心体的质量随时间做如下的变化：

(42)

由于这种对接会导致卫星中心刚体的尺寸和质量发生改变，从而影响到系统的转动惯量值，导致卫星结构的某些阶次的模态参数值发生突变。假设该对接过程并不会对卫星的整体质心位置造成影响，当然这只是一种比较理想的情况，在实际的空间对接情况中，由于对接的结构分布的不同，航天器的质心将发生改变，从而导致航天器动力学方程中的参数将更加复杂，因此这里质心不变的情况只是为了简化建模步骤和后续讨论而作的假设。那么原RPBSID和改进后的递推方法对于发生突变的第5、7、9和11阶频率值的辨识结果如图4所示。

图4 两种方法辨识得到的系统时变频率值Fig.4 Identification results of system time-varying frequencies with two methods

从图4的结果中可以看出，与文献[16]中对于参数突变系统的辨识结论相一致，基于预测器的这两类辨识方法在频率值发生突变的时间点处需要一个较长的迭代过程来使得递推结果趋于稳定，但是对于突变后的稳定跟踪阶段还是能够有效地跟踪的。如果不考虑两个突变阶段的较大误差，两种方法所得到的各阶时变频率和阻尼比的平均相对误差值如表3所示，结果证明这种改进的递推方法可以较为准确的辨识突变系统的频率值，但辨识的阻尼比结果与原始值相比仍然存在着较大的误差。

表3 两种方法所得到的频率和阻尼比的平均相对误差Table 3 Average relative errors of frequencies and damping ratios for two methods

工况3：模态参数周期变化的情况

图5 两种方法对于系统时变频率的辨识结果Fig.5 Identification results of system time-varying frequencies for two methods

表4 两种方法对于第7和第9阶时变频率值的平均相对误差Table 4 Average relative errors of the 7th and 9th time-varying frequencies for two methods

在算例的最后，我们通过MATLAB软件的仿真结果，对比这两种方法的计算时间，以验证2.4节计算复杂度的理论结果。为了更方便的比对计算结果，我们分别统计这两种递推方法在系统模型阶次n分别为24、30、36和48时的计算时间(每组进行30次蒙特卡罗实验)，则这两种方法的仿真计算效率结果如图7所示。从图7中可以看出，改进的递推方法与原方法相比，在应用于系统阶次较高的模型辨识时其计算优势更加明显，这是和上文关于该算法计算复杂度的理论分析结果相符合的。由于实际航天器对象的系统模型阶次往往选取得比较高，并考虑到在线辨识与控制参数实时修正的需求，这种计算效率的改进将具有重要的意义。

图6 两种方法对于系统时变频率的辨识结果Fig.6 Identification results of system time-varying frequencies for two methods

表5 两种方法对于第7和第9阶时变频率值的平均相对误差Table 5 Average relative errors of the 7th and 9th time-varying frequencies for two methods

图7 两种方法所用的平均计算时间Fig.7 Average computation time of two methods

4 结 论

本文提出了一种改进的RPBSID方法并应用于航天器模态参数的辨识。不同于传统的子空间或RPBSID等参数辨识方法，这种改进方法利用仿射投影和最小二乘技术来实现状态量的递推辨识，从而避免了传统方法在计算系统状态量的过程中，由于奇异值分解或者构建广义Hankel矩阵所导致的数据量较大的问题，提高了方法的计算效率。仿真结果证明了该方法能够有效得到系统的时变模态参数，与传统的子空间方法相比具有更高的计算效率。

由于这种方法是基于RPBSID算法而提出，因此还存在着一些未来需要解决的问题：(1)该方法需要一定的先验知识，例如参数p的选取往往需要提前知道系统的阶次n。而且这类方法需要一定的迭代次数来逐步逼近于实际值，例如图2中初始时间所示的情况，从而达到参数值的稳定跟踪；(2)这种方法主要适用于慢时变系统，例如工况1的情况；而对于变化较快的系统，这种递推方法的跟踪效果将会显著变差。三种工况的验证结果也能反映出这种方法需要一定的反应时间来达到参数跟踪的目的，因此对于慢变系统的跟踪效果较好，通过RPBSID方法的原始作者所提供的MATLAB源程序算例和对应的文献[12,16]所给出的结论也证明了这一点。因此，如何提高这种方法对于快变系统的辨识精度，是未来需要继续探索和深入研究的问题。