SINS任意失准角无奇异快速传递对准

崔 潇，秦永元，严恭敏，周 琪

(1. 西北工业大学自动化学院，西安 710129；2. 西安飞行自动控制研究所，西安 710065；3. 飞行器控制一体化技术国防科技重点实验室，西安 710065)

0 引 言

随着现代战争对武器装备精确打击能力和快速反应能力的要求日益提高，许多舰载和机载武器装备都安装了捷联惯性导航系统(Strapdown inertial navigation system, SINS),而由于惯导系统为战术级，传递对准成为其初始对准的主要方案[1-3]。因此，研究战术武器系统的快速高精度传递对准具有较大的工程应用价值。

自1989年Kain和Cloutier[1]介绍了“速度+姿态”匹配的快速传递对准方法以来，传递对准进入快速发展和应用阶段，于1998年在F-16战机上进行了试飞验证,仅在摇翼机动下，10 s内达到了1mrad的对准精度[2]。随后传递对准研究主要集中在匹配方法、滤波模型和影响对准精度的干扰因素等方面[3-6]。

传统的传递对准大都是以系统的误差模型为基础的，传统方案主要分为两类滤波估计问题：即基于小失准角假设的线性滤波估计问题和基于大失准角假设的非线性滤波估计问题。

针对大失准角对准时，目前采用的方法主要有两种，一是传递对准姿态装订时，对子惯导进行安装角补偿，以期满足小角度要求，然后进行传统线性模型传递对准；二是采用非线性滤波模型和滤波算法。很多学者建立了以姿态角、姿态四元数或旋转矢量为姿态描述的非线性误差模型[7-11]，可适用于大失准角下的传递对准，虽然这类模型的量测方程为线性，但系统方程均具有强非线性，各种诸如CDPF[7]、UKF[8-10]、SRUKF[11]等非线性滤波被引入到对准算法，存在计算量较大且在大失准角下估计精度不高等问题。

为了适应任意失准角条件下的快速传递对准，文献[12]研究了二次对准方案，首先在大失准角较大时采用基于四元数的非线性模型，在估计达到一定精度后，对子惯导进行补偿，再切换到基于欧拉角的线性模型；文献[13]提出了在惯性系框架内完成传递对准的思路，建立基于罗德里格参数的大失准角传递对准方案，设计了二阶EKF滤波算法，但由于罗德里格参数描述姿态的奇异性，需在对准过程中对奇异点进行判别和处理。

本文主要在文献[13]的基础上，研究了任意失准角下无奇异点的快速传递对准方案，建立了惯性系下基于姿态矩阵的统一线性对准模型，采用了惯性系内比力积分+角速度积分的匹配方案，推导了矩阵形式的约束卡尔曼滤波实现，所建立的滤波模型和采用的滤波算法，与失准角大小无关，在形式上和实现上完全一致，同时也避免了罗德里格参数对准模型的奇异点问题。

1 惯性系统—对准模型

1.1 主子惯导系统实际测量值基本关系

由文献[13-14]可知，主子惯导系统敏感的比力和角速度在地心惯性系内的投影关系分别为：

(1)

(2)

假设在传递对准开始时刻，将主子惯导坐标系m和s均进行惯性凝固，分别得到惯性坐标系im和is。对准过程中姿态变化可利用陀螺仪输出进行跟踪，忽略主惯导误差时，即有

(3)

(4)

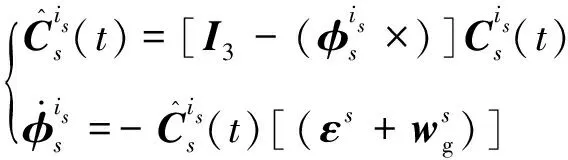
(5)

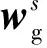
(6)

(7)

对于子惯导同理可得

(8)

将式(8)展开整理，略去高阶小量，可得

(9)

由式(1)、式(7)、式(9)可得

(10)

对主子惯导系统测量的角速度信息进行类似处理，可得

(11)

式中：

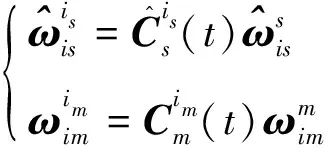
(12)

式(10)和式(11)表明，可以采用主子惯导系统实际测量值在惯性系内的投影作为惯性系传递对准的匹配量，这种匹配方式与经典的传递对准中基于测量参数匹配方式，即加速度和角速度匹配对应。

1.2 传递对准模型

式(10)和式(11)等号两端包含了相关误差，若对其进行积分操作，则能够有效平滑相关噪声、杆臂残差以及弹性变形项，提高信噪比。

对式(10)等号左边取积分，并记

(13)

对式(10)等号右边括号内取积分，并记

(14)

由式(10)、式(13)、式(14)可得

(15)

对式(11)进行类似操作，同理可得

(16)

其中,

(17)

(18)

式(15)为比力量测的直接积分，可作为惯性系传递对准的匹配量，与经典传递对准算法中的速度匹配类似；式(16)则为角速度量测的直接积分，也是惯性系传递对准的匹配量之一，与经典传递对准算法中的姿态匹配类似。

值得注意的是，在推导式(15)和式(16)的过程中，并未对主子惯导系统之间的相对姿态提出任何假设。无论主子惯导系统之间相对姿态为小姿态角还是大姿态角，惯性系内得到的匹配方程具有一致的形式，因此，可以在惯性系内，设计出无需区分相对姿态大小的统一的传递对准模型，由于模型基于姿态矩阵表示，避免了文献[13]中奇异点问题，下面将以比力积分加角速度积分匹配为基础，来设计基于姿态矩阵任意失准角下的无奇异快速传递对准算法。

(19)

考虑陀螺漂移和加速度计零偏为随机常值，即

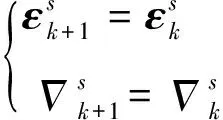
(20)

(21)

(22)

式中：Eij为8×8矩阵，且第ij个元素为1，其余为0。

由式(15)、式(16)可构成量测方程，即

(23)

其中，Vk+1为量测噪声矩阵，且

(24)

2 滤波器设计

式(21)、式(23)描述的滤波模型具有下面三个特征：1)系统方程和量测方程均为线性；2)状态为矩阵形式；3)部分状态，即姿态矩阵受到正交约束。针对上述三个特征，设计如下矩阵滤波算法来实现对参数的估计。

2.1 滤波时间更新

要利用标准卡尔曼滤波基本方程，首先要将式(21)、式(23)矩阵方程向量化，为此定义如下向量化算子：

x=vec(X)

(25)

式中：X∈Rm×n,x∈Rmn×1，即向量化算子vec(·)表示将矩阵X按列首尾相连得到向量x，也称按列堆栈[15]。

若定义⊗为Kronecker积，则[15]

vec(AXB)=(BT⊗A)vec(X)

(26)

假设在tk时刻状态Xk和估计均方误差阵Pk已知，对式(21)进行向量化操作，并利用式(26)特性，可得

vec(Wk)

(27)

即等价于标准卡尔曼滤波离散状态方程

xk+1=Ψkxk+wk

(28)

则状态一步预测

(29)

利用算子vec的线性特性和式(26)，则式(29)可等价于

(30)

一步预测均方误差

(31)

式中：Qk=cov{Wk}。

式(30)和式(31)即为矩阵滤波的时间更新。

2.2 滤波量测更新

对式(23)描述的量测方程，首先忽略姿态矩阵正交约束的影响，推导量测更新算法。

记量测一步预测

(32)

残差

(33)

对式(33)进行向量化操作，即

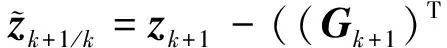
(34)

则由标准卡尔曼滤波可得

Sk+1=Γk+1Pk+1/k(Γk+1)T+Rk+1

(35)

Kk+1=Pk+1/k(Γk+1)T(Sk+1)-1

(36)

(37)

式中：Γk+1=(Gk+1)T⊗Hk+1。

为了将式(37)恢复到矩阵形式，引入如下定理：对于给定矩阵X∈Ri3×i4,Z∈Ri1×i2，且A∈Ri1i2×i3i4，定义z∈Ri1i2,x∈Ri3i4分别为矩阵Z,X向量化的向量，即z=vec(Z),x=vec(X)。将矩阵写成如下分块矩阵的形式

(38)

其中，Ajl∈Ri1×i3，则向量化方程:

z=Ax

(39)

等价于如下矩阵方程

(40)

式中：Elj∈Ri4×i2，且第lj个元素为1，其余元素为0。定理的详细证明过程参见文献[16]。

将定理应用于式(37)右端第二项，其余项则利用向量化算子的逆运算，可得

(41)

(42)

式(41)则为矩阵状态在时刻tk+1的更新方程。

由标准卡尔曼滤波理论，矩阵估计均方误差为

Pk+1/k+1= (I24-Kk+1Γk+1)Pk+1/k(I24-Kk+1Γk+1)T+

(43)

式(33)、式(35)、式(36)、式(41)和式(43)即为不考虑约束条件下所设计的矩阵滤波量测更新。

2.3 姿态矩阵正交约束下滤波算法

针对滤波算法中的姿态矩阵正交约束问题，借鉴伪量测处理方法，推导本文所设计的滤波算法在姿态矩阵正交约束条件下的实现。

考虑下式约束

(44)

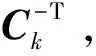
(45)

(46)

伪量测方程(46)为姿态矩阵Ck的线性方程，很自然可运用到矩阵卡尔曼滤波的量测更新过程中，即在进行正常的矩阵卡尔曼量测更新之后，接着进行如下正交化量测更新过程

Sk+1=Pk+1/k+μortI9

(47)

Kk+1=Pk+1/k(Sk+1)-1

(48)

(49)

Pk+1/k+1= (I9-Kk+1)Pk+1/k(I9-Kk+1)T+

(50)

3 仿真与分析

为进一步检验本文所提的基于矩阵卡尔曼滤波传递对准方法的性能，进行了传递对准的数字仿真。

3.1 仿真条件

1)以舰船在水中会受到来自风浪的干扰而发生绕俯仰轴、横滚轴和方位轴的摇摆运动为例。这种运动可看作由一系列幅值和频率相近的正弦波来描述[9-10]：

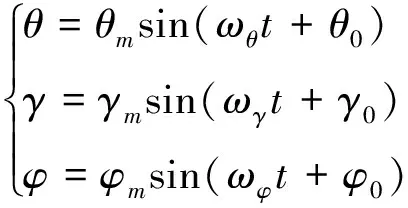
(51)

式中：θ,γ,φ分别为绕俯仰轴,横滚轴和方位轴的摇摆角度；θm,γm,φm分别为摇摆角度幅值；ωθ,ωγ,ωφ为摇摆的角频率；θ0,γ0,φ0为摇摆的初始相位。

表1 摇摆参数设置Table 1 Simulation parameters of swaying

2)子惯导参数设置如表2所示。

表2 子惯导参数设置Table 2 Sensors specifications of SINS

3)滤波器参数设置：矩阵状态变量初值为X(0)=03×8，系统噪声取为陀螺、加速度计噪声。由于系统方程中未考虑挠曲变形及载体振动等干扰，这里适当增大量测噪声，比力量测噪声取为0.001 m/s2，角速度积分量测取为5×10-6(°)/s。

4)主子惯导安装误差角设置：小失准角[1° 1° 1°]T和大失准角[60° 60° 150°]T。

3.2 仿真结果

根据第3.1节设置的仿真条件，分别在大、小失准角条件下进行了50次蒙特卡洛仿真，两种情况下的仿真结果如图1～图4所示。图中实线表示本文提出的MKF方法，虚线表示传统方法。其中，小角度条件下，传统方法采用的是线性模型的速度+姿态匹配方案；而大失准角条件下，同时对比了文献[8-10]中基于非线性模型的传统UKF方案和文献[13]提出的二阶EKF(EKF2)方案。

从图1～图4可以看出，无论失准角大小，矩阵滤波对准方案具有同样的估计效果，估计速度明显优于传统方法，而且在估计收敛之后的稳态性能也优于传统方法，尤其是在大失准角时，优势较传统UKF更为明显，而且具有快速性特点，传统UKF方法在大失准角时，精度有所下降，由于本文采用文献[13]相同的量测匹配方案，因此对准精度同EKF2相当。

两种失准角情形下的估计均值和估计误差均方根统计结果(50次)如表3所示。结果表明，无论失准角大小，基于矩阵滤波对准方案三个失准角估计精度都能达到0.03°(误差均方根)以下，均优于传统线性模型和非线性模型方法。该方案兼顾了传递对准的快速性和准确性。

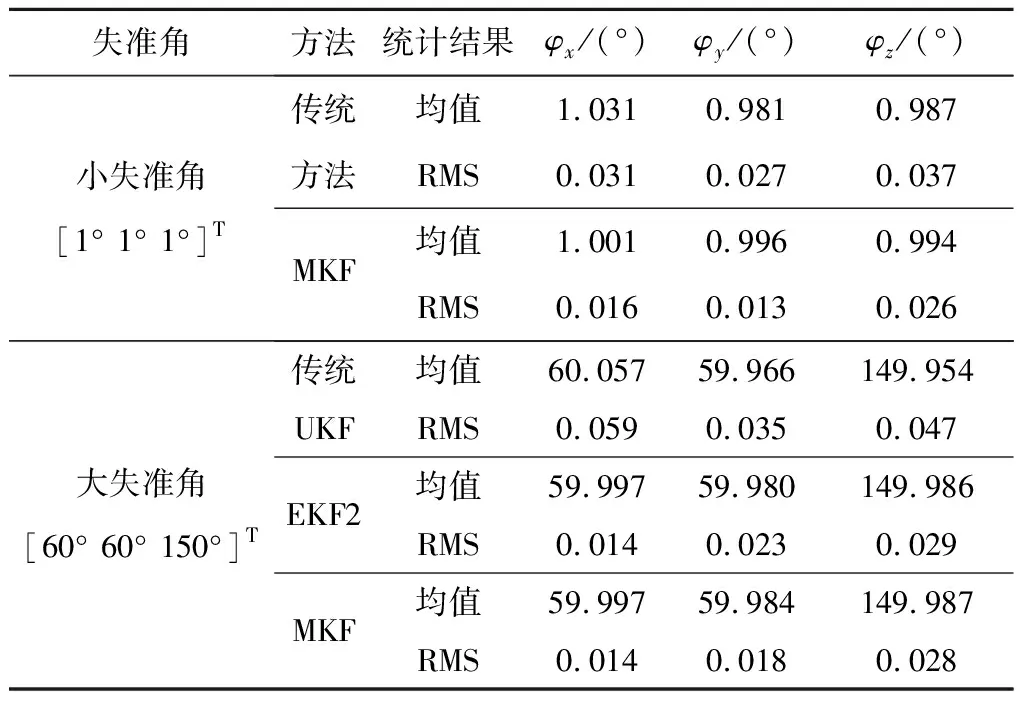
表3 失准角估计结果Table 3 Monte-Carlo means and RMS of the misalignment

4 结 论

针对传统传递对准需区分失准角大小而确定对准模型和滤波算法的问题，提出以姿态矩阵为状态的统一无奇异传递对准模型，并推导了基于比力积分+角速度积分为量测的矩阵卡尔曼滤波传递对准滤波算法，该算法适用于任意失准角，且与传统方法相比，无需初值、无需主惯导初始参数装订，即传递对准不再区分粗、精过程。仿真结果表明，无论失准角大小，在摇摆运动下算法均能够在10 s内快速完成对准,相比于传统对准方法，精度和快速性均有所提高，为战术武器任意失准角条件下的快速传递对准提供了参考。